Análisis de componentes principales del kernel.

Técnica estadística multivariada

En el campo de la estadística multivariada , el análisis de componentes principales del kernel (kernel PCA) ^[1] es una extensión del análisis de componentes principales (PCA) que utiliza técnicas de métodos del kernel . Usando un kernel, las operaciones originalmente lineales de PCA se realizan en un espacio de Hilbert del kernel en reproducción .

Antecedentes: PCA lineal

Recuerde que el PCA convencional opera con datos centrados en cero; eso es,

${\displaystyle {\frac {1}{N}}\sum _{i=1}^{N}\mathbf {x} _{i}=\mathbf {0} }$,

donde es una de las observaciones multivariadas. Opera diagonalizando la matriz de covarianza , ${\displaystyle \mathbf {x} _{i}}$ ${\displaystyle N}$

${\displaystyle C={\frac {1}{N}}\sum _{i=1}^{N}\mathbf {x} _{i}\mathbf {x} _{i}^{\top }}$

en otras palabras, da una descomposición propia de la matriz de covarianza:

${\displaystyle \lambda \mathbf {v} =C\mathbf {v} }$

que se puede reescribir como

${\displaystyle \lambda \mathbf {x} _{i}^{\top }\mathbf {v} =\mathbf {x} _{i}^{\top }C\mathbf {v} \quad {\textrm {for}}~i=1,\ldots ,N}$. ^[2]

(Ver también: Matriz de covarianza como operador lineal )

Introducción del Kernel a PCA

Para comprender la utilidad del PCA del núcleo, particularmente para la agrupación, observe que, si bien N puntos, en general, no pueden separarse linealmente en dimensiones, casi siempre pueden separarse linealmente en dimensiones. Es decir, dados N puntos, si los asignamos a un espacio N -dimensional con ${\displaystyle d<N}$ ${\displaystyle d\geq N}$ ${\displaystyle \mathbf {x} _{i}}$

${\displaystyle \Phi (\mathbf {x} _{i})}$dónde , ${\displaystyle \Phi :\mathbb {R} ^{d}\to \mathbb {R} ^{N}}$

es fácil construir un hiperplano que divida los puntos en grupos arbitrarios. Por supuesto, esto crea vectores linealmente independientes, por lo que no hay covarianza sobre la cual realizar la descomposición propia explícitamente como lo haríamos en PCA lineal. ${\displaystyle \Phi }$

En cambio, en el kernel PCA, se "elige" una función arbitraria y no trivial que nunca se calcula explícitamente, lo que permite la posibilidad de utilizar funciones de dimensiones muy altas si nunca tenemos que evaluar los datos en ese espacio. Como generalmente intentamos evitar trabajar en el espacio, al que llamaremos 'espacio de características', podemos crear el kernel N-by-N. ${\displaystyle \Phi }$ ${\displaystyle \Phi }$ ${\displaystyle \Phi }$

${\displaystyle K=k(\mathbf {x} ,\mathbf {y} )=(\Phi (\mathbf {x} ),\Phi (\mathbf {y} ))=\Phi (\mathbf {x} )^{T}\Phi (\mathbf {y} )}$

que representa el espacio del producto interno (ver matriz de Gramian ) del espacio de características que de otro modo sería intratable. La forma dual que surge en la creación de un núcleo nos permite formular matemáticamente una versión de PCA en la que nunca resolvemos los vectores propios y valores propios de la matriz de covarianza en el espacio (ver Truco del núcleo ). Los N elementos en cada columna de K representan el producto escalar de un punto de los datos transformados con respecto a todos los puntos transformados (N puntos). En el siguiente ejemplo se muestran algunos núcleos conocidos. ${\displaystyle \Phi (\mathbf {x} )}$

Debido a que nunca trabajamos directamente en el espacio de características, la formulación central de PCA está restringida en el sentido de que no calcula los componentes principales en sí, sino las proyecciones de nuestros datos sobre esos componentes. Evaluar la proyección desde un punto en el espacio de características sobre el k-ésimo componente principal (donde el superíndice k significa el componente k, no potencias de k) ${\displaystyle \Phi (\mathbf {x} )}$ ${\displaystyle V^{k}}$

${\displaystyle {V^{k}}^{T}\Phi (\mathbf {x} )=\left(\sum _{i=1}^{N}\mathbf {a} _{i}^{k}\Phi (\mathbf {x} _{i})\right)^{T}\Phi (\mathbf {x} )}$

Observamos que denota producto escalar, que son simplemente los elementos del núcleo . Parece que todo lo que queda es calcular y normalizar , lo que se puede hacer resolviendo la ecuación del vector propio ${\displaystyle \Phi (\mathbf {x} _{i})^{T}\Phi (\mathbf {x} )}$ ${\displaystyle K}$ ${\displaystyle \mathbf {a} _{i}^{k}}$

${\displaystyle N\lambda \mathbf {a} =K\mathbf {a} }$

donde es el número de puntos de datos en el conjunto, y y son los valores propios y vectores propios de . Luego, para normalizar los vectores propios , requerimos que ${\displaystyle N}$ ${\displaystyle \lambda }$ ${\displaystyle \mathbf {a} }$ ${\displaystyle K}$ ${\displaystyle \mathbf {a} ^{k}}$

${\displaystyle 1=(V^{k})^{T}V^{k}}$

Se debe tener cuidado con el hecho de que, tenga o no media cero en su espacio original, no se garantiza que esté centrado en el espacio de características (que nunca calculamos explícitamente). Dado que se requieren datos centrados para realizar un análisis de componentes principales eficaz, " centralizamos " para convertirnos en ${\displaystyle x}$ ${\displaystyle K}$ ${\displaystyle K'}$

${\displaystyle K'=K-\mathbf {1_{N}} K-K\mathbf {1_{N}} +\mathbf {1_{N}} K\mathbf {1_{N}} }$

donde denota una matriz N por N para la cual cada elemento toma valor . Usamos para realizar el algoritmo PCA del kernel descrito anteriormente. ${\displaystyle \mathbf {1_{N}} }$ ${\displaystyle 1/N}$ ${\displaystyle K'}$

Aquí se debe ilustrar una advertencia sobre la PCA del núcleo. En PCA lineal, podemos usar los valores propios para clasificar los vectores propios en función de la cantidad de variación de los datos que captura cada componente principal. Esto es útil para reducir la dimensionalidad de los datos y también podría aplicarse a KPCA. Sin embargo, en la práctica hay casos en que todas las variaciones de los datos son iguales. Esto suele deberse a una elección incorrecta de la escala del kernel.

Grandes conjuntos de datos

En la práctica, un conjunto de datos grande conduce a una K grande, y almacenar K puede convertirse en un problema. Una forma de lidiar con esto es realizar agrupaciones en el conjunto de datos y llenar el núcleo con los medios de esas agrupaciones. Dado que incluso este método puede producir una K relativamente grande, es común calcular solo los valores propios P ​​superiores y los vectores propios de los valores propios se calculan de esta manera.

Ejemplo

Puntos de entrada antes de la PCA del kernel

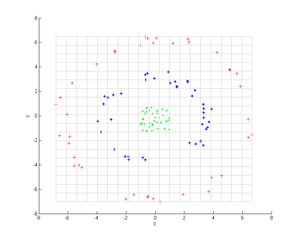
Considere tres nubes concéntricas de puntos (mostradas); Deseamos utilizar la PCA del kernel para identificar estos grupos. El color de los puntos no representa información involucrada en el algoritmo, solo muestra cómo la transformación reubica los puntos de datos.

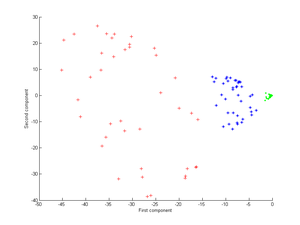
Primero, considere el núcleo.

${\displaystyle k({\boldsymbol {x}},{\boldsymbol {y}})=({\boldsymbol {x}}^{\mathrm {T} }{\boldsymbol {y}}+1)^{2}}$

Al aplicar esto al kernel PCA se obtiene la siguiente imagen.

Salida después de la PCA del kernel con . Los tres grupos se pueden distinguir utilizando únicamente el primer componente. ${\displaystyle k({\boldsymbol {x}},{\boldsymbol {y}})=({\boldsymbol {x}}^{\mathrm {T} }{\boldsymbol {y}}+1)^{2}}$

Consideremos ahora un núcleo gaussiano:

${\displaystyle k({\boldsymbol {x}},{\boldsymbol {y}})=e^{\frac {-||{\boldsymbol {x}}-{\boldsymbol {y}}||^{2}}{2\sigma ^{2}}},}$

Es decir, este núcleo es una medida de cercanía, igual a 1 cuando los puntos coinciden e igual a 0 en el infinito.

Salida después del kernel PCA, con un kernel gaussiano .

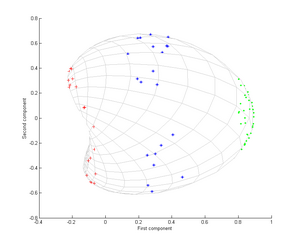
Tenga en cuenta en particular que el primer componente principal es suficiente para distinguir los tres grupos diferentes, lo cual es imposible usando solo PCA lineal, porque el PCA lineal opera solo en el espacio dado (en este caso bidimensional), en el que estas nubes de puntos concéntricos están no linealmente separable.

Aplicaciones

Se ha demostrado que Kernel PCA es útil para la detección de novedades ^[3] y la eliminación de ruido de imágenes. ^[4]

Ver también

• Análisis de conglomerados
• Reducción de dimensionalidad no lineal.
• Agrupación espectral

Referencias

1. Schölkopf, Bernhard; Smola, Alex; Müller, Klaus-Robert (1998). "Análisis de componentes no lineales como un problema de valores propios del núcleo". Computación neuronal . 10 (5): 1299-1319. CiteSeerX  10.1.1.100.3636 . doi :10.1162/089976698300017467. S2CID  6674407.
2. Scholkopf, Bernhard; Smola, Alejandro; Müller, Klaus-Robert (diciembre de 1996). Análisis de componentes no lineales como problema de valores propios del kernel (PDF) (Reporte técnico). Max-Planck-Institut für biologische Kybernetik. 44.
3. Hoffmann, Heiko (2007). "Kernel PCA para la detección de novedades". Reconocimiento de patrones . 40 (3): 863–874. Código Bib : 2007PatRe..40..863H. doi :10.1016/j.patcog.2006.07.009.
4. Kernel PCA y eliminación de ruido en espacios destacados. NIPS, 1999