El secreto compartido de Shamir

Cryptographic algorithm created by Adi Shamir

El algoritmo de intercambio de secretos de Shamir (SSS) es un algoritmo de intercambio de secretos eficiente para distribuir información privada (el "secreto") entre un grupo. El secreto no puede revelarse a menos que un quórum del grupo actúe en conjunto para poner en común su conocimiento. Para lograr esto, el secreto se divide matemáticamente en partes (las "partes") a partir de las cuales el secreto se puede volver a ensamblar solo cuando se combina una cantidad suficiente de partes. SSS tiene la propiedad de seguridad de teoría de la información , lo que significa que incluso si un atacante roba algunas partes, es imposible que el atacante reconstruya el secreto a menos que haya robado la cantidad de partes del quórum.

El intercambio de secretos de Shamir se utiliza en algunas aplicaciones para compartir las claves de acceso a un secreto maestro.

Explicación de alto nivel

SSS se utiliza para proteger un secreto de forma distribuida, generalmente para proteger claves de cifrado . El secreto se divide en varias partes que, individualmente, no proporcionan ninguna información sobre el secreto.

Para reconstruir un secreto protegido por SSS, se necesita una cantidad de acciones, denominada umbral . No se puede obtener información sobre el secreto de ninguna cantidad de acciones por debajo del umbral (una propiedad denominada secreto perfecto ). En este sentido, SSS es una generalización del bloc de notas de un solo uso (que puede verse como SSS con un umbral de dos acciones y dos acciones en total). ^[1]

Ejemplo de aplicación

Una empresa necesita proteger su bóveda. Si una sola persona conoce el código de la bóveda, este podría perderse o no estar disponible cuando sea necesario abrirla. Si hay varias personas que conocen el código, es posible que no confíen entre sí para actuar siempre de manera honesta.

En esta situación, se puede utilizar SSS para generar acciones del código de la bóveda que se distribuyen entre las personas autorizadas de la empresa. Se puede seleccionar el umbral mínimo y la cantidad de acciones que se le otorgan a cada persona de modo que la bóveda sea accesible únicamente para (grupos de) personas autorizadas. Si se presentan menos acciones que el umbral, no se puede abrir la bóveda.

Por accidente, por coacción o como acto de oposición, algunas personas pueden presentar información incorrecta en sus acciones. Si el total de acciones correctas no alcanza el umbral mínimo, la bóveda permanece bloqueada.

Casos de uso

El secreto compartido de Shamir se puede utilizar para

• compartir una clave para descifrar la clave raíz de un administrador de contraseñas , ^[2]
• recuperar una clave de usuario para acceder a correo electrónico cifrado ^[3] y
• compartir la frase de contraseña utilizada para recrear un secreto maestro, que a su vez se utiliza para acceder a una billetera de criptomonedas . ^[4]

Propiedades y debilidades

El SSS tiene propiedades útiles, pero también debilidades ^[5] que significan que no es adecuado para algunos usos.

Las propiedades útiles incluyen:

1. Seguro : El esquema tiene seguridad basada en la teoría de la información .
2. Mínimo : El tamaño de cada pieza no excede el tamaño de los datos originales.
3. Extensible : para cualquier umbral determinado, se pueden agregar o eliminar acciones de forma dinámica sin afectar las acciones existentes.
4. Dinámica : Se puede mejorar la seguridad sin cambiar el secreto, pero cambiando el polinomio ocasionalmente (manteniendo el mismo término libre) y construyendo una nueva parte para cada uno de los participantes.
5. Flexible : En las organizaciones donde la jerarquía es importante, a cada participante se le pueden asignar diferentes cantidades de acciones según su importancia dentro de la organización. Por ejemplo, con un umbral de 3, el presidente podría desbloquear la caja fuerte solo si se le dan tres acciones, mientras que tres secretarios con una acción cada uno deben combinar sus acciones para desbloquear la caja fuerte.

Las debilidades incluyen:

1. No se puede verificar el intercambio de secretos : durante el proceso de reagrupación de acciones, SSS no ofrece una forma de verificar la exactitud de cada acción que se utiliza. El intercambio de secretos verificable tiene como objetivo verificar que los accionistas sean honestos y no envíen acciones falsas.
2. Punto único de falla : el secreto debe existir en un lugar cuando se divide en partes y nuevamente en un lugar cuando se vuelve a ensamblar. Estos son puntos de ataque y otros esquemas, incluida la firma múltiple, eliminan al menos uno de estos puntos únicos de falla .

Historia

Adi Shamir , un científico israelí , formuló por primera vez el esquema en 1979. ^[6]

Principio matemático

El esquema explota el teorema de interpolación de Lagrange , específicamente que los puntos en el polinomio determinan de manera única un polinomio de grado menor o igual a . Por ejemplo, 2 puntos son suficientes para definir una línea , 3 puntos son suficientes para definir una parábola , 4 puntos para definir una curva cúbica y así sucesivamente. ${\displaystyle k}$ ${\displaystyle k-1}$

Formulación matemática

El método de compartición de secretos de Shamir es un esquema de umbral ideal y perfecto basado en la interpolación polinómica sobre cuerpos finitos . En dicho esquema, el objetivo es dividir un secreto (por ejemplo, la combinación de una caja fuerte ) en fragmentos de datos (conocidos como partes ) de tal manera que: ${\displaystyle \left(k,n\right)}$ ${\displaystyle S}$ ${\displaystyle n}$ ${\displaystyle S_{1},\ldots ,S_{n}}$

1. El conocimiento de una o más acciones hace que sea computable, es decir, que el secreto completo se puede reconstruir a partir de cualquier combinación de acciones. ${\displaystyle k}$ ${\displaystyle S_{i}}$ ${\displaystyle S}$ ${\displaystyle S}$ ${\displaystyle k}$
2. El conocimiento de una cantidad de acciones o de una cantidad menor de ellas deja una indeterminación total, en el sentido de que los valores posibles para siguen siendo tan probables con el conocimiento de hasta acciones como con el conocimiento de acciones. El secreto no se puede reconstruir con menos de acciones. ${\displaystyle k-1}$ ${\displaystyle S_{i}}$ ${\displaystyle S}$ ${\displaystyle S}$ ${\displaystyle k-1}$ ${\displaystyle 0}$ ${\displaystyle S}$ ${\displaystyle k}$

Si , entonces se necesitan todas las acciones para reconstruir el secreto . ${\displaystyle n=k}$ ${\displaystyle S}$

Se pueden dibujar un número infinito de polinomios de grado 2 a través de 2 puntos. Se requieren 3 puntos para determinar de forma única un polinomio de grado 2. Esta imagen es solo para fines ilustrativos: el esquema de Shamir usa polinomios sobre un campo finito, que no son fáciles de representar en un plano bidimensional.

Supongamos que el secreto puede representarse como un elemento de un campo finito (donde es mayor que el número de acciones que se generan). Elija aleatoriamente elementos, , de y construya el polinomio . Calcule los puntos de la curva, por ejemplo, establezca para encontrar los puntos . A cada participante se le da un punto (una entrada distinta de cero al polinomio y la salida correspondiente). ^[7] Dado cualquier subconjunto de de estos pares, se puede obtener utilizando interpolación , con una posible fórmula para hacerlo siendo , donde la lista de puntos en el polinomio se da como pares de la forma . Nótese que es igual al primer coeficiente del polinomio . ${\displaystyle S}$ ${\displaystyle a_{0}}$ ${\displaystyle \mathrm {GF} (q)}$ ${\displaystyle q}$ ${\displaystyle n}$ ${\displaystyle k-1}$ ${\displaystyle a_{1},\cdots ,a_{k-1}}$ ${\displaystyle \mathrm {GF} (q)}$ ${\displaystyle f\left(x\right)=a_{0}+a_{1}x+a_{2}x^{2}+a_{3}x^{3}+\cdots +a_{k-1}x^{k-1}}$ ${\displaystyle n}$ ${\displaystyle i=1,\ldots ,n}$ ${\displaystyle \left(i,f\left(i\right)\right)}$ ${\displaystyle k}$ ${\displaystyle a_{0}}$ ${\displaystyle a_{0}=f(0)=\sum _{j=0}^{k-1}y_{j}\prod _{\begin{smallmatrix}m\,=\,0\\m\,\neq \,j\end{smallmatrix}}^{k-1}{\frac {x_{m}}{x_{m}-x_{j}}}}$ ${\displaystyle k}$ ${\displaystyle (x_{i},y_{i})}$ ${\displaystyle f(0)}$ ${\displaystyle f(x)}$

Ejemplo de cálculo

El siguiente ejemplo ilustra la idea básica. Sin embargo, tenga en cuenta que los cálculos en el ejemplo se realizan utilizando aritmética de números enteros en lugar de aritmética de cuerpos finitos para que la idea sea más fácil de entender. Por lo tanto, el siguiente ejemplo no proporciona un secreto perfecto y no es un ejemplo adecuado del esquema de Shamir. El siguiente ejemplo explicará el problema.

Preparación

Supongamos que el secreto a compartir es 1234 . ${\displaystyle (S=1234)}$

En este ejemplo, el secreto se dividirá en 6 partes , donde cualquier subconjunto de 3 partes es suficiente para reconstruir el secreto. Los números se toman al azar. Sean 166 y 94. ${\displaystyle (n=6)}$ ${\displaystyle (k=3)}$ ${\displaystyle k-1=2}$

Esto produce coeficientes donde está el secreto. ${\displaystyle (a_{0}=1234;a_{1}=166;a_{2}=94),}$ ${\displaystyle a_{0}}$

El polinomio para producir acciones secretas (puntos) es por tanto:

${\displaystyle f(x)=1234+166x+94x^{2}}$

Seis puntos del polinomio se construyen como: ${\displaystyle D_{x-1}=(x,f(x))}$

${\displaystyle D_{0}=(1,1494);D_{1}=(2,1942);D_{2}=(3,2578);D_{3}=(4,3402);D_{4}=(5,4414);D_{5}=(6,5614)}$

Cada participante del esquema recibe un punto diferente (un par de y ). Porque se utiliza en lugar de los puntos que empiezan desde y no desde . Esto es necesario porque es el secreto. ${\displaystyle x}$ ${\displaystyle f(x)}$ ${\displaystyle D_{x-1}}$ ${\displaystyle D_{x}}$ ${\displaystyle (1,f(1))}$ ${\displaystyle (0,f(0))}$ ${\displaystyle f(0)}$

Reconstrucción

Para reconstruir el secreto son suficientes 3 puntos cualesquiera

Considere utilizar los 3 puntos . ${\displaystyle \left(x_{0},y_{0}\right)=\left(2,1942\right);\left(x_{1},y_{1}\right)=\left(4,3402\right);\left(x_{2},y_{2}\right)=\left(5,4414\right)}$

Cálculo de los polinomios de base de Lagrange :

${\displaystyle \ell _{0}(x)={\frac {x-x_{1}}{x_{0}-x_{1}}}\cdot {\frac {x-x_{2}}{x_{0}-x_{2}}}={\frac {x-4}{2-4}}\cdot {\frac {x-5}{2-5}}={\frac {1}{6}}x^{2}-{\frac {3}{2}}x+{\frac {10}{3}}}$

${\displaystyle \ell _{1}(x)={\frac {x-x_{0}}{x_{1}-x_{0}}}\cdot {\frac {x-x_{2}}{x_{1}-x_{2}}}={\frac {x-2}{4-2}}\cdot {\frac {x-5}{4-5}}=-{\frac {1}{2}}x^{2}+{\frac {7}{2}}x-5}$

${\displaystyle \ell _{2}(x)={\frac {x-x_{0}}{x_{2}-x_{0}}}\cdot {\frac {x-x_{1}}{x_{2}-x_{1}}}={\frac {x-2}{5-2}}\cdot {\frac {x-4}{5-4}}={\frac {1}{3}}x^{2}-2x+{\frac {8}{3}}}$

Usando la fórmula para interpolación polinomial, es: ${\displaystyle f(x)}$

${\displaystyle {\begin{aligned}f(x)&=\sum _{j=0}^{2}y_{j}\cdot \ell _{j}(x)\\[6pt]&=y_{0}\ell _{0}(x)+y_{1}\ell _{1}(x)+y_{2}\ell _{2}(x)\\[6pt]&=1942\left({\frac {1}{6}}x^{2}-{\frac {3}{2}}x+{\frac {10}{3}}\right)+3402\left(-{\frac {1}{2}}x^{2}+{\frac {7}{2}}x-5\right)+4414\left({\frac {1}{3}}x^{2}-2x+{\frac {8}{3}}\right)\\[6pt]&=1234+166x+94x^{2}\end{aligned}}}$

Recordando que el secreto es el coeficiente libre, lo que significa que , y el secreto ha sido recuperado. ${\displaystyle S=1234}$

Enfoque computacionalmente eficiente

El uso de la interpolación polinomial para encontrar un coeficiente en un polinomio fuente utilizando polinomios de Lagrange no es eficiente , ya que se calculan constantes no utilizadas. ${\displaystyle S=f(0)}$

Considerando esto, una fórmula optimizada para utilizar polinomios de Lagrange para encontrar se define de la siguiente manera: ${\displaystyle f(0)}$

${\displaystyle f(0)=\sum _{j=0}^{k-1}y_{j}\prod _{\begin{smallmatrix}m\,=\,0\\m\,\neq \,j\end{smallmatrix}}^{k-1}{\frac {x_{m}}{x_{m}-x_{j}}}}$

Problema de uso de la aritmética de números enteros

Aunque la versión simplificada del método demostrado arriba, que utiliza aritmética de números enteros en lugar de aritmética de campos finitos, funciona, existe un problema de seguridad: Eve obtiene información sobre cada uno de los que encuentra. ${\displaystyle S}$ ${\displaystyle D_{i}}$

Supongamos que encuentra los 2 puntos y . Todavía no tiene puntos, por lo que en teoría no debería haber obtenido más información sobre . Pero podría combinar la información de los 2 puntos con la información pública: . Al hacerlo, Eve podría realizar la siguiente operación algebraica: ${\displaystyle D_{0}=(1,1494)}$ ${\displaystyle D_{1}=(2,1942)}$ ${\displaystyle k=3}$ ${\displaystyle S}$ ${\displaystyle n=6,k=3,f(x)=a_{0}+a_{1}x+\cdots +a_{k-1}x^{k-1},a_{0}=S,a_{i}\in \mathbb {Z} }$

1. Rellene la fórmula con y el valor de ${\displaystyle f(x)}$ ${\displaystyle S}$ ${\displaystyle k:f(x)=S+a_{1}x+\cdots +a_{k-1}x^{k-1}\Rightarrow {}f(x)=S+a_{1}x+a_{2}x^{2}}$
2. Rellene (1) con los valores de 's y ${\displaystyle D_{0}}$ ${\displaystyle x}$ ${\displaystyle f(x):1494=S+a_{1}1+a_{2}1^{2}\Rightarrow {}1494=S+a_{1}+a_{2}}$
3. Rellene (1) con los valores de 's y ${\displaystyle D_{1}}$ ${\displaystyle x}$ ${\displaystyle f(x):1942=S+a_{1}2+a_{2}2^{2}\Rightarrow {}1942=S+2a_{1}+4a_{2}}$
4. Restar (3)-(2): y reescribir esto como . ${\displaystyle (1942-1494)=(S-S)+(2a_{1}-a_{1})+(4a_{2}-a_{2})\Rightarrow {}448=a_{1}+3a_{2}}$ ${\displaystyle a_{1}=448-3a_{2}}$
5. Ahora, Eva puede reemplazar el resultado de (4) en (2): lo que la lleva a la información de que S es par. ${\displaystyle 1494=S+(448-3a_{2})+a_{2}\Rightarrow {}S=1046+2a_{2}}$

Solución utilizando aritmética de campos finitos

Esta es una curva polinomial sobre un campo finito: el orden del polinomio aparentemente tiene poco que ver con la forma del gráfico.

El ataque anterior explota las restricciones sobre los valores que puede tomar el polinomio en virtud de cómo fue construido: el polinomio debe tener coeficientes que sean números enteros y el polinomio debe tomar un número entero como valor cuando se evalúa en cada una de las coordenadas utilizadas en el esquema. Esto reduce sus posibles valores en puntos desconocidos, incluido el secreto resultante, dado que hay menos de acciones. ${\displaystyle k}$

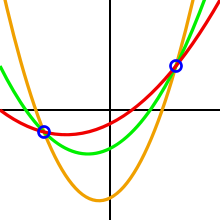
Este problema se puede solucionar utilizando aritmética de campos finitos. Un campo finito siempre tiene un tamaño , donde es un primo y es un entero positivo. El tamaño del campo debe satisfacer , y que sea mayor que el número de valores posibles para el secreto, aunque la última condición se puede evitar dividiendo el secreto en valores secretos más pequeños y aplicando el esquema a cada uno de ellos. En nuestro ejemplo a continuación, utilizamos un campo primo (es decir, r = 1). La figura muestra una curva polinómica sobre un campo finito. ${\displaystyle q=p^{r}}$ ${\displaystyle p}$ ${\displaystyle r}$ ${\displaystyle q}$ ${\displaystyle q>n}$ ${\displaystyle q}$

En la práctica, esto es sólo un pequeño cambio. El orden q del campo (es decir, el número de valores que tiene) debe elegirse para que sea mayor que el número de participantes y el número de valores que el secreto puede tomar. Todos los cálculos que involucran el polinomio también deben calcularse sobre el campo (mod p en nuestro ejemplo, en el que se toma como un primo) en lugar de sobre los números enteros. Tanto la elección del campo como la asignación del secreto a un valor en este campo se consideran de conocimiento público. ${\displaystyle a_{0}=S}$ ${\displaystyle p=q}$

Para este ejemplo, elija , por lo que el polinomio se convierte en que da los puntos: ${\displaystyle p=1613}$ ${\displaystyle f(x)=1234+166x+94x^{2}{\bmod {1613}}}$ ${\displaystyle (1,1494);(2,329);(3,965);(4,176);(5,1188);(6,775)}$

Esta vez Eva no obtiene ninguna información cuando encuentra un (hasta que tiene puntos). ${\displaystyle D_{x}}$ ${\displaystyle k}$

Supongamos nuevamente que Eve encuentra y , y la información pública es: . Al intentar el ataque anterior, Eve puede: ${\displaystyle D_{0}=\left(1,1494\right)}$ ${\displaystyle D_{1}=\left(2,329\right)}$ ${\displaystyle n=6,k=3,p=1613,f(x)=a_{0}+a_{1}x+\dots +a_{k-1}x^{k-1}\mod {p},a_{0}=S,a_{i}\in \mathbb {N} }$

1. Rellene la fórmula con y el valor de y : ${\displaystyle f(x)}$ ${\displaystyle S}$ ${\displaystyle k}$ ${\displaystyle p}$ ${\displaystyle f(x)=S+a_{1}x+\dots +a_{3-1}x^{3-1}\mod 1613}$
2. Rellene (1) con los valores de 's y ${\displaystyle D_{0}}$ ${\displaystyle x}$ ${\displaystyle f(x):1494\equiv S+a_{1}1+a_{2}1^{2}{\pmod {1613}}\Rightarrow {}1494\equiv S+a_{1}+a_{2}{\pmod {1613}}}$
3. Rellene (1) con los valores de 's y ${\displaystyle D_{1}}$ ${\displaystyle x}$ ${\displaystyle f(x):1942\equiv S+a_{1}2+a_{2}2^{2}{\pmod {1613}}\Rightarrow {}1942\equiv S+2a_{1}+4a_{2}{\pmod {1613}}}$
4. Restar (3)-(2): y reescribir esto como ${\displaystyle (1942-1494)\equiv (S-S)+(2a_{1}-a_{1})+(4a_{2}-a_{2}){\pmod {1613}}\Rightarrow {}448\equiv a_{1}+3a_{2}{\pmod {1613}}}$ ${\displaystyle a_{1}\equiv 448-3a_{2}{\pmod {1613}}}$

Existen valores posibles para . Ella sabe que siempre disminuye en 3, por lo que si fuera divisible por ella podría concluir . Sin embargo, es primo, por lo que no puede concluir esto. Por lo tanto, usar un cuerpo finito evita este posible ataque. ${\displaystyle p}$ ${\displaystyle a_{1}}$ ${\displaystyle [448,445,442,\ldots ]}$ ${\displaystyle p}$ ${\displaystyle 3}$ ${\displaystyle a_{1}\in [1,4,7,\ldots ]}$ ${\displaystyle p}$

Además, aunque Eve puede concluir que , no proporciona ninguna información adicional, ya que el comportamiento de "envolvimiento" de la aritmética modular evita la fuga de "S es par", a diferencia del ejemplo con aritmética de enteros anterior. ${\displaystyle S\equiv 1046+2a_{2}{\pmod {1613}}}$

Código Python

Para mantener el código más claro, aquí se utiliza un campo principal. En la práctica, por conveniencia, un esquema construido utilizando un campo binario más pequeño se puede aplicar por separado a pequeñas subcadenas de bits del secreto (por ejemplo, GF(256) para la aplicación byte a byte), sin pérdida de seguridad. La condición estricta de que el tamaño del campo debe ser mayor que el número de porciones debe respetarse (por ejemplo, si el número de porciones pudiera superar 255, el campo GF(256) podría reemplazarse por, digamos, GF(65536)).

""" La siguiente implementación de Python del intercambio de secretos de Shamir se publica en el dominio público bajo los términos de CC0 y OWFa: https://creativecommons.org/publicdomain/zero/1.0/ http://www.openwebfoundation.org/legal/the-owf-1-0-agreements/owfa-1-0Consulte las últimas líneas para ver el uso. Probado en Python 2 y 3. """desde  __future__  importar  división desde  __future__  importar  función_impresiónimportar  funciones de importación aleatorias # 12.° Mersenne Prime _PRIME  =  2  **  127  -  1_RINT  =  herramientasfuncionales . parcial ( aleatorio . SystemRandom () . randint ,  0 )def  _eval_at ( poly ,  x ,  prime ): """Evalúa el polinomio (tupla de coeficiente) en x, utilizado para generar un  grupo shamir en make_random_shares a continuación.  """ accum = 0 para coeficiente en reverso ( poly ): accum *= x acumulación += coeff acumulación %= acumulación de rendimiento principal                   def  make_random_shares ( secret ,  minimum ,  shares ,  prime = _PRIME ): """  Genera un grupo aleatorio de shamir para un secreto dado, devuelve puntos de participación.  """ if minimum > shares : raise ValueError ( "El secreto del grupo sería irrecuperable." ) poly = [ secret ] + [ _RINT ( prime - 1 ) for i in range ( minimum - 1 )] points = [( i , _eval_at ( poly , i , prime )) for i in range ( 1 , shares + 1 )] return points                                   def  _extended_gcd ( a ,  b ): """  La división de números enteros módulo p significa hallar la inversa del  denominador módulo p y luego multiplicar el numerador por esta  inversa (Nota: la inversa de A es B tal que A*B % p == 1). Esto se puede  calcular mediante el algoritmo euclidiano extendido  http://en.wikipedia.org/wiki/Shamir%27s_Secret_Sharing/Modular_multiplicative_inverse#Computation  """ x = 0 last_x = 1 y = 1 last_y = 0 while b != 0 : quot = a // b a , b = b , a % b x , last_x = last_x - quot * x , x y , last_y = last_y - quot * y , y return last_x , last_y                                                  def  _divmod ( num ,  den ,  p ): """Calcular num / den módulo primo p  Para explicar esto, el resultado será tal que:  den * _divmod(num, den, p) % p == num  """  inv ,  _  =  _extended_gcd ( den ,  p )  return  num  *  invdef  _lagrange_interpolate ( x ,  x_s ,  y_s ,  p ): """  Encuentra el valor de y para x dado, dados n (x, y) puntos;  k puntos definirán un polinomio de hasta k-ésimo orden.  """ k = len ( x_s ) assert k == len ( set ( x_s )), "los puntos deben ser distintos" def PI ( vals ): # PI en mayúsculas -- producto de entradas accum = 1 for v in vals : accum *= v return accum nums = [] # evita la división inexacta dens = [] for i in range ( k ) : others = list ( x_s ) cur = others.pop ( i ) nums.append ( PI ( x - o for o in others ) ) dens . append ( PI ( cur - o para o en otros )) den = PI ( dens ) num = suma ([ _divmod ( nums [ i ] * den * y_s [ i ] % p , dens [ i ], p ) para i en rango ( k )]) return ( _divmod ( num , den , p ) + p ) % p                                                                                 def  recover_secret ( shares ,  prime = _PRIME ): """  Recupera el secreto de los puntos compartidos  (puntos (x,y) en el polinomio).  """ if len ( shares ) < 3 : raise ValueError ( "necesita al menos tres shares" ) x_s , y_s = zip ( * shares ) return _lagrange_interpolate ( 0 , x_s , y_s , prime )                def  main (): """Función principal""" secreto = 1234 acciones = make_random_shares ( secreto , mínimo = 3 , acciones = 6 )          print ( 'Secreto: ' ,  secreto )  print ( 'Acciones:' )  si  acciones :  para  compartir  en  acciones :  print ( ' ' ,  compartir ) print ( 'Secreto recuperado de un subconjunto mínimo de acciones: ' ,  recover_secret ( shares [: 3 ]))  print ( 'Secreto recuperado de un subconjunto mínimo diferente de acciones: ' ,  recover_secret ( shares [ - 3 :]))si  __nombre__  ==  '__main__' :  principal ()

Véase también

• Intercambio de secretos
• Computación segura entre múltiples partes
• Polinomio de Lagrange
• Intercambio de secretos homomórficos : un protocolo de votación descentralizado y simplista
• Regla de dos hombres
• Contraseña parcial

Referencias

1. Krenn, Stephan; Loruenser, Thomas (2023). Introducción al intercambio de secretos: una descripción general sistemática y una guía para la selección de protocolos . doi :10.1007/978-3-031-28161-7. ISBN 978-3-031-28160-0.
2. "Sellado/Dessellado". Bóveda de HashiCorp . Consultado el 2 de octubre de 2022 .
3. "Reseña de PreVeil". PCMag . Consultado el 2 de octubre de 2022 .
4. Rusnak, Pavol; Kozlik, Andrew; Vejpustek, Ondrej; Susanka, Tomas; Palatinus, Marek; Hoenicke, Jochen (18 de diciembre de 2017). "SLIP-0039: Shamir's Secret-Sharing for Mnemonic Codes". GitHub . SatoshiLabs . Consultado el 3 de octubre de 2022 . Este SLIP describe una implementación estándar e interoperable del intercambio de secretos de Shamir (SSS) y una especificación para su uso en la copia de seguridad de las carteras deterministas jerárquicas descritas en BIP-0032.
5. Lopp, Jameson (1 de octubre de 2020). "Deficiencias del sistema de intercambio de secretos de Shamir" . Consultado el 3 de octubre de 2022. Se han implementado varias variaciones del sistema de intercambio de secretos de Shamir (SSS) en el espacio de las criptomonedas, solo para que los desarrolladores se dieran cuenta más tarde de que la complejidad adicional terminó reduciendo la seguridad del sistema.
6. Shamir, Adi (1979), "Cómo compartir un secreto", Comunicaciones de la ACM , 22 (11): 612–613, doi : 10.1145/359168.359176 , S2CID  16321225
7. Knuth, DE (1997), El arte de la programación informática , vol. II: Algoritmos seminuméricos (3.ª ed.), Addison-Wesley, pág. 505.

Lectura adicional

• Dawson, E.; Donovan, D. (1994), "La amplitud del plan de compartición de secretos de Shamir", Computers & Security , 13 : 69–78, doi :10.1016/0167-4048(94)90097-3.
• Benzekki, K. (2017). "Un enfoque de compartición de secretos verificable para almacenamiento seguro en múltiples nubes". Ubiquitous Networking . Lecture Notes in Computer Science. Vol. 10542. Casablanca: Springer. págs. 225–234. doi :10.1007/978-3-319-68179-5_20. ISBN 978-3-319-68178-8..

Enlaces externos

• El secreto compartido de Shamir en la biblioteca Crypto++
• Esquema de intercambio de secretos de Shamir (ssss): una implementación de la GPL de GNU
• sharedsecret – implementación en Go
• s4 - Herramienta para compartir secretos de Shamir en línea que utiliza el algoritmo de HashiCorp para compartir secretos de Shamir
• Shamir39 - versión web en iancoleman.io
• kn Secrets - versión web en un sitio web dedicado, cuyo objetivo es hacer que el intercambio de secretos de Shamir sea lo más accesible posible