Timsort es un algoritmo de ordenamiento híbrido y estable , derivado del ordenamiento por fusión y el ordenamiento por inserción , diseñado para funcionar bien en muchos tipos de datos del mundo real. Fue implementado por Tim Peters en 2002 para su uso en el lenguaje de programación Python . El algoritmo encuentra subsecuencias de los datos que ya están ordenados (ejecuciones) y las usa para ordenar el resto de manera más eficiente. Esto se hace fusionando ejecuciones hasta que se cumplan ciertos criterios. Timsort ha sido el algoritmo de ordenamiento estándar de Python desde la versión 2.3 (desde la versión 3.11 usando la política de fusión Powersort [5] ), y se usa para ordenar matrices de tipo no primitivo en Java SE 7 , [6] en la plataforma Android , [7] en GNU Octave , [8] en V8 , [9] Swift , [10] e inspiró el algoritmo de ordenamiento usado en Rust . [11]
Utiliza técnicas del artículo de Peter McIlroy de 1993 "Optimistic Sorting and Information Theoretic Complexity" [12] .
Timsort fue diseñado para aprovechar las ejecuciones de elementos ordenados consecutivos que ya existen en la mayoría de los datos del mundo real, las ejecuciones naturales . Itera sobre los datos recopilando elementos en ejecuciones y colocando simultáneamente esas ejecuciones en una pila. Siempre que las ejecuciones en la parte superior de la pila coincidan con un criterio de fusión, se fusionan. Esto continúa hasta que se recorren todos los datos; luego, todas las ejecuciones se fusionan de dos en dos y solo queda una ejecución ordenada. La ventaja de fusionar ejecuciones ordenadas en lugar de fusionar sublistas de tamaño fijo (como se hace con la ordenación por fusión tradicional) es que disminuye la cantidad total de comparaciones necesarias para ordenar la lista completa.
Cada ejecución tiene un tamaño mínimo, que se basa en el tamaño de la entrada y se define al comienzo del algoritmo. Si una ejecución es más pequeña que este tamaño mínimo, se utiliza la ordenación por inserción para agregar más elementos a la ejecución hasta que se alcance el tamaño mínimo.

Timsort es un algoritmo de clasificación estable (se mantiene el orden de los elementos con la misma clave) y busca realizar fusiones equilibradas (una fusión fusiona ejecuciones de tamaños similares).
Para lograr estabilidad de ordenación, solo se fusionan ejecuciones consecutivas. Entre dos ejecuciones no consecutivas, puede haber un elemento con la misma clave dentro de las ejecuciones. La fusión de esas dos ejecuciones cambiaría el orden de las claves iguales. Ejemplo de esta situación ([] son ejecuciones ordenadas): [1 2 2] 1 4 2 [0 1 2]
En la búsqueda de fusiones equilibradas, Timsort considera tres ejecuciones en la parte superior de la pila, X , Y , Z , y mantiene las invariantes:
Si se viola alguna de estas invariantes, Y se fusiona con la menor de X o Z y las invariantes se verifican nuevamente. Una vez que las invariantes se cumplen, puede comenzar la búsqueda de una nueva ejecución en los datos. [14] Estas invariantes mantienen las fusiones como aproximadamente equilibradas mientras se mantiene un compromiso entre retrasar la fusión para lograr el equilibrio, explotar la nueva ocurrencia de ejecuciones en la memoria caché y hacer que las decisiones de fusión sean relativamente simples.
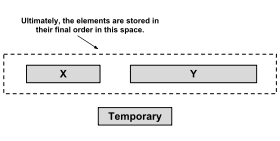
La implementación original de la ordenación por combinación no está en el lugar y tiene una sobrecarga de espacio de N (tamaño de los datos). Existen implementaciones de ordenación por combinación en el lugar, pero tienen una sobrecarga de tiempo alta. Para lograr un término medio, Timsort realiza una ordenación por combinación con una pequeña sobrecarga de tiempo y una sobrecarga de espacio menor que N.
En primer lugar, Timsort realiza una búsqueda binaria para encontrar la ubicación donde se insertaría el primer elemento de la segunda ejecución en la primera ejecución ordenada, manteniéndola ordenada. Luego, realiza el mismo algoritmo para encontrar la ubicación donde se insertaría el último elemento de la primera ejecución en la segunda ejecución ordenada, manteniéndola ordenada. Los elementos antes y después de estas ubicaciones ya están en su lugar correcto y no necesitan ser fusionados. Luego, la ejecución reducida más pequeña se copia en la memoria temporal y los elementos copiados se fusionan con la ejecución reducida más grande en el espacio ahora libre. Si la ejecución reducida más a la izquierda es más pequeña, la fusión procede de izquierda a derecha. Si la ejecución reducida más a la derecha es más pequeña, la fusión procede de derecha a izquierda (es decir, comenzando con los elementos en los extremos del espacio temporal y la ejecución más a la izquierda, y llenando el espacio libre desde su final). Esta optimización reduce la cantidad de movimientos de elementos necesarios, el tiempo de ejecución y la sobrecarga de espacio temporal en el caso general.
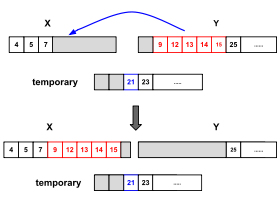
Ejemplo: se deben fusionar dos ejecuciones [1, 2, 3, 6, 10] y [4, 5, 7, 9, 12, 14, 17]. Nótese que ambas ejecuciones ya están ordenadas individualmente. El elemento más pequeño de la segunda ejecución es 4 y se tendría que agregar en la cuarta posición de la primera ejecución para preservar su orden (asumiendo que la primera posición de una ejecución es 1). El elemento más grande de la primera ejecución es 10 y se tendría que agregar en la quinta posición de la segunda ejecución para preservar su orden. Por lo tanto, [1, 2, 3] y [12, 14, 17] ya están en sus posiciones finales y las ejecuciones en las que se requieren movimientos de elementos son [6, 10] y [4, 5, 7, 9]. Con este conocimiento, solo necesitamos asignar un buffer temporal de tamaño 2 en lugar de 4.
La fusión se puede realizar en ambas direcciones: de izquierda a derecha, como en la fusión tradicional, o de derecha a izquierda.

Una fusión individual de las ejecuciones R1 y R2 mantiene el recuento de elementos consecutivos seleccionados de una ejecución. Cuando este número alcanza el umbral de galope mínimo ( min_gallop ), Timsort considera que es probable que aún se puedan seleccionar muchos elementos consecutivos de esa ejecución y cambia al modo de galope. Supongamos que R1 es responsable de activarlo. En este modo, el algoritmo realiza una búsqueda en dos etapas para el lugar en la ejecución R1 donde se insertaría el siguiente elemento x de la ejecución R2. En la primera etapa realiza una búsqueda exponencial , también conocida como búsqueda galopante, hasta encontrar un k tal que R1[2 k−1 − 1] < x <= R1[2 k − 1], es decir, una región de incertidumbre que comprende 2 k−1 − 1 elementos consecutivos de R1. La segunda etapa realiza una búsqueda binaria directa de esta región para encontrar la ubicación exacta en R1 para x . El modo galopante es un intento de adaptar el algoritmo de fusión al patrón de intervalos entre elementos en las ejecuciones.
El galope no siempre es eficiente. En algunos casos, el modo de galope requiere más comparaciones que una simple búsqueda lineal . Según los puntos de referencia realizados por el desarrollador, el galope es beneficioso solo cuando el elemento inicial de una ejecución no es uno de los primeros siete elementos de la otra ejecución. Esto implica un umbral inicial de 7. Para evitar los inconvenientes del modo de galope, se toman dos acciones: (1) Cuando se descubre que el galope es menos eficiente que la búsqueda binaria , se sale del modo de galope. (2) El éxito o el fracaso del galope se utiliza para ajustar min_gallop . Si el elemento seleccionado es de la misma matriz que devolvió un elemento anteriormente, min_gallop se reduce en uno, lo que fomenta el regreso al modo de galope. De lo contrario, el valor se incrementa en uno, lo que desalienta el regreso al modo de galope. En el caso de datos aleatorios, el valor de min_gallop se vuelve tan grande que el modo de galope nunca se repite. [15]
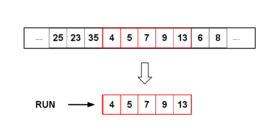
Para aprovechar también los datos ordenados en orden descendente, Timsort invierte las ejecuciones estrictamente descendentes cuando las encuentra y las agrega a la pila de ejecuciones. Dado que las ejecuciones descendentes se invierten luego ciegamente, excluir las ejecuciones con elementos iguales mantiene la estabilidad del algoritmo; es decir, los elementos iguales no se invertirán.
Debido a que la fusión es más eficiente cuando el número de ejecuciones es igual o ligeramente menor que una potencia de dos, y notablemente menos eficiente cuando el número de ejecuciones es ligeramente mayor que una potencia de dos, Timsort elige minrun para intentar garantizar la primera condición. [13]
Minrun se elige del rango de 32 a 64 inclusive, de modo que el tamaño de los datos, dividido por minrun , sea igual o ligeramente menor que una potencia de dos. El algoritmo final toma los seis bits más significativos del tamaño de la matriz, suma uno si alguno de los bits restantes está establecido y utiliza ese resultado como minrun . Este algoritmo funciona para todas las matrices, incluidas aquellas más pequeñas que 64; para matrices de tamaño 63 o menos, esto establece minrun igual al tamaño de la matriz y Timsort se reduce a una ordenación por inserción. [13]
En el peor de los casos , Timsort realiza comparaciones para ordenar una matriz de n elementos. En el mejor de los casos, que ocurre cuando la entrada ya está ordenada, se ejecuta en tiempo lineal, lo que significa que es un algoritmo de ordenamiento adaptativo . [3]
Es superior a Quicksort para ordenar referencias o punteros de objetos porque estos requieren una costosa indirección de memoria para acceder a los datos y realizar comparaciones y los beneficios de coherencia de caché de Quicksort se reducen en gran medida.
En 2015, investigadores holandeses y alemanes del proyecto ENVISAGE del 7PM de la UE encontraron un error en la implementación estándar de Timsort. [16] Se solucionó en 2015 en Python, Java y Android.
En concreto, las invariantes en los tamaños de ejecución apilados garantizan un límite superior estricto en el tamaño máximo de la pila requerida. La implementación asignó previamente una pila suficiente para ordenar 2 64 bytes de entrada y evitó más controles de desbordamiento.
Sin embargo, la garantía requiere que los invariantes se apliquen a cada grupo de tres ejecuciones consecutivas, pero la implementación solo lo verificó para los tres primeros. [16] Al utilizar la herramienta KeY para la verificación formal del software Java, los investigadores descubrieron que esta verificación no es suficiente y pudieron encontrar longitudes de ejecución (y entradas que generaron esas longitudes de ejecución) que darían como resultado que los invariantes se violaran más profundamente en la pila después de que se fusionara la parte superior de la pila. [17]
Como consecuencia, para ciertas entradas, el tamaño asignado no es suficiente para contener todas las ejecuciones no fusionadas. En Java, esto genera para esas entradas una excepción de matriz fuera de límites. La entrada más pequeña que activa esta excepción en Java y Android v7 es de tamaño67 108 864 (2 26 ). (Las versiones anteriores de Android ya activaban esta excepción para ciertas entradas de tamaño65 536 (2 16 ))
La implementación de Java se corrigió aumentando el tamaño de la pila preasignada en función de un análisis actualizado del peor de los casos. El artículo también mostró mediante métodos formales cómo establecer el invariante deseado comprobando que las cuatro ejecuciones superiores de la pila satisfacen las dos reglas anteriores. Este enfoque fue adoptado inicialmente por Python [18] hasta que cambió a Powersort en 2022 con el lanzamiento de Python 3.11. [5]
[Timsort] también tiene aspectos positivos: es estable (los elementos que se comparan de forma igual conservan su orden relativo, por lo que, por ejemplo, si ordenas primero por código postal y una segunda vez por nombre, las personas con el mismo nombre siguen apareciendo en orden ascendente de código postal; esto es importante en aplicaciones que, por ejemplo, refinan los resultados de las consultas en función de la entrada del usuario). ... No tiene casos malos (O(N log N) es el peor caso; las comparaciones N−1 son las mejores).
TimSort es un intrigante algoritmo de ordenamiento diseñado en 2002 para Python, cuya complejidad en el peor de los casos se anunció, pero no se demostró hasta nuestra reciente preimpresión.
Código robado en gran parte de listobject.c de Python, que no tenía encabezado de licencia. Sin embargo, gracias a Tim Peters por las partes del código que robé.
El algoritmo actual es un ordenamiento por fusión adaptativo e iterativo inspirado en timsort. Está diseñado para ser muy rápido en los casos en los que el segmento está casi ordenado o consta de dos o más secuencias ordenadas concatenadas una tras otra.