El cálculo de las propiedades del vidrio ( modelado del vidrio ) se utiliza para predecir las propiedades de interés del vidrio o el comportamiento del vidrio bajo ciertas condiciones (por ejemplo, durante la producción) sin investigación experimental, basándose en datos y experiencias anteriores, con la intención de ahorrar tiempo, materiales, recursos financieros y ambientales, o para obtener conocimientos científicos. Fue practicado por primera vez a fines del siglo XIX por A. Winkelmann y O. Schott . La combinación de varios modelos de vidrio junto con otras funciones relevantes se puede utilizar para la optimización y los procedimientos de seis sigma . En forma de análisis estadístico, el modelado del vidrio puede ayudar con la acreditación de nuevos datos, procedimientos experimentales e instituciones de medición (laboratorios de vidrio).
Históricamente, el cálculo de las propiedades del vidrio está directamente relacionado con la fundación de la ciencia del vidrio . A finales del siglo XIX, el físico Ernst Abbe desarrolló ecuaciones que permiten calcular el diseño de microscopios ópticos optimizados en Jena , Alemania , estimulado por la cooperación con el taller óptico de Carl Zeiss . Antes de la época de Ernst Abbe, la construcción de microscopios era principalmente una obra de arte y una artesanía experimentada, lo que daba como resultado microscopios ópticos muy caros y de calidad variable. Ahora Ernst Abbe sabía exactamente cómo construir un microscopio excelente, pero lamentablemente, no existían las lentes y prismas necesarios con proporciones específicas de índice de refracción y dispersión . Ernst Abbe no pudo encontrar respuestas a sus necesidades en los artistas e ingenieros del vidrio; la fabricación del vidrio no se basaba en la ciencia en ese momento. [2]
En 1879, el joven ingeniero de vidrio Otto Schott envió a Abbe muestras de vidrio con una composición especial ( vidrio de silicato de litio ) que había preparado él mismo y que esperaba que mostrara propiedades ópticas especiales . Tras las mediciones de Ernst Abbe, las muestras de vidrio de Schott no tenían las propiedades deseadas, y tampoco eran tan homogéneas como se deseaba. No obstante, Ernst Abbe invitó a Otto Schott a trabajar más en el problema y a evaluar sistemáticamente todos los componentes posibles del vidrio. Finalmente, Schott logró producir muestras de vidrio homogéneas e inventó el vidrio de borosilicato con las propiedades ópticas que Abbe necesitaba. [2] Estos inventos dieron lugar a las conocidas empresas Zeiss y Schott Glass (véase también Cronología de la tecnología de microscopios ). Nació la investigación sistemática del vidrio. En 1908, Eugene Sullivan fundó la investigación del vidrio también en Estados Unidos ( Corning , Nueva York ). [3]
Al principio de la investigación del vidrio, lo más importante era conocer la relación entre la composición del vidrio y sus propiedades. Para este propósito, Otto Schott introdujo el principio de aditividad en varias publicaciones para el cálculo de las propiedades del vidrio. [4] [5] [6] Este principio implica que la relación entre la composición del vidrio y una propiedad específica es lineal para todas las concentraciones de los componentes del vidrio, asumiendo una mezcla ideal , con C i y b i representando concentraciones específicas de los componentes del vidrio y coeficientes relacionados respectivamente en la ecuación siguiente. El principio de aditividad es una simplificación y solo es válido dentro de rangos de composición estrechos como se ve en los diagramas mostrados para el índice de refracción y la viscosidad. Sin embargo, la aplicación del principio de aditividad abrió el camino a muchas de las invenciones de Schott, incluidos los vidrios ópticos, los vidrios con baja expansión térmica para cocinar y utensilios de laboratorio ( Duran ) y los vidrios con depresión reducida del punto de congelación para termómetros de mercurio . Posteriormente, English [7] y Gehlhoff et al. [8] publicaron modelos similares de cálculo de propiedades del vidrio aditivo. El principio de aditividad de Schott todavía se usa ampliamente hoy en día en la investigación y la tecnología del vidrio. [9] [10]

Schott y muchos científicos e ingenieros aplicaron posteriormente el principio de aditividad a datos experimentales medidos en su propio laboratorio dentro de rangos de composición suficientemente estrechos ( modelos de vidrio locales ). Esto es más conveniente porque no es necesario considerar los desacuerdos entre laboratorios ni las interacciones no lineales de los componentes del vidrio. En el transcurso de varias décadas de investigación sistemática sobre el vidrio, se estudiaron miles de composiciones de vidrio , lo que dio como resultado millones de propiedades del vidrio publicadas, recopiladas en bases de datos sobre el vidrio . Este enorme conjunto de datos experimentales no se investigó en su totalidad hasta que Bottinga, [13] Kucuk, [14] Priven, [15] Choudhary, [16] Mazurin, [17] y Fluegel [18] [19] publicaron sus modelos globales de vidrio , utilizando varios enfoques. A diferencia de los modelos de Schott, los modelos globales consideran muchas fuentes de datos independientes, lo que hace que las estimaciones del modelo sean más confiables. Además, los modelos globales pueden revelar y cuantificar influencias no aditivas de ciertas combinaciones de componentes del vidrio sobre las propiedades, como el efecto de álcali mixto que se ve en el diagrama adyacente, o la anomalía del boro . Los modelos globales también reflejan desarrollos interesantes de la precisión de la medición de las propiedades del vidrio , por ejemplo, una precisión decreciente de los datos experimentales en la literatura científica moderna para algunas propiedades del vidrio, que se muestra en el diagrama. Pueden usarse para la acreditación de nuevos datos, procedimientos experimentales e instituciones de medición (laboratorios de vidrio). En las siguientes secciones (excepto la entalpía de fusión) se presentan técnicas de modelado empírico , que parecen ser una forma exitosa de manejar enormes cantidades de datos experimentales. Los modelos resultantes se aplican en la ingeniería y la investigación contemporáneas para el cálculo de las propiedades del vidrio.
Existen modelos de vidrio no empíricos ( deductivos ). [20] A menudo no se crean para obtener predicciones confiables de las propiedades del vidrio en primer lugar (excepto la entalpía de fusión), sino para establecer relaciones entre varias propiedades (por ejemplo, radio atómico , masa atómica , fuerza y ángulos de enlace químico , valencia química , capacidad térmica ) para obtener conocimiento científico. En el futuro, la investigación de las relaciones de propiedades en modelos deductivos puede conducir en última instancia a predicciones confiables para todas las propiedades deseadas, siempre que las relaciones de propiedades se comprendan bien y todos los datos experimentales requeridos estén disponibles.
Las propiedades y el comportamiento del vidrio durante la producción se pueden calcular mediante el análisis estadístico de bases de datos de vidrio como GE-SYSTEM [21], SciGlass [22] e Interglad [23] , a veces combinado con el método de elementos finitos . Para estimar la entalpía de fusión se utilizan bases de datos termodinámicas.
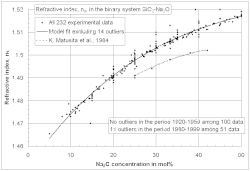
Si la propiedad del vidrio deseada no está relacionada con la cristalización (por ejemplo, la temperatura de liquidus ) o la separación de fases , se puede aplicar una regresión lineal utilizando funciones polinómicas comunes hasta el tercer grado. A continuación se muestra un ejemplo de ecuación de segundo grado. Los valores C son las concentraciones de componentes del vidrio como Na2O o CaO en porcentaje u otras fracciones, los valores b son coeficientes y n es el número total de componentes del vidrio. El componente principal del vidrio, sílice (SiO2 ) , se excluye en la siguiente ecuación debido a la sobreparametrización debido a la restricción de que todos los componentes suman el 100%. Muchos términos en la siguiente ecuación se pueden descuidar en función del análisis de correlación y significancia . Los errores sistemáticos como los que se ven en la imagen se cuantifican mediante variables ficticias . Hay más detalles y ejemplos disponibles en un tutorial en línea de Fluegel. [24]
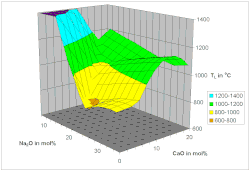
La temperatura del líquido se ha modelado mediante regresión no lineal utilizando redes neuronales [26] y funciones de pico desconectadas. [25] El enfoque de funciones de pico desconectadas se basa en la observación de que dentro de un campo de fase cristalina primaria se puede aplicar la regresión lineal [27] y en los puntos eutécticos ocurren cambios repentinos.
La entalpía de fusión del vidrio refleja la cantidad de energía necesaria para convertir la mezcla de materias primas ( lote ) en un vidrio fundido. Depende de la composición del lote y del vidrio, de la eficiencia del horno y de los sistemas de regeneración de calor, del tiempo medio de residencia del vidrio en el horno y de muchos otros factores. Carl Kröger escribió un artículo pionero sobre el tema en 1953. [28]
Para modelar el flujo de vidrio en un horno de fundición de vidrio , se aplica comercialmente el método de elementos finitos , [29] [30] basándose en datos o modelos de viscosidad , densidad , conductividad térmica , capacidad térmica , espectros de absorción y otras propiedades relevantes del vidrio fundido. El método de elementos finitos también se puede aplicar a los procesos de formación de vidrio.
A menudo es necesario optimizar varias propiedades del vidrio simultáneamente, incluidos los costos de producción. [21] [31] Esto se puede realizar, por ejemplo, mediante una búsqueda simplex o en una hoja de cálculo de la siguiente manera:
Es posible ponderar las propiedades deseadas de forma diferente. Se puede encontrar información básica sobre el principio en un artículo de Huff et al. [33]. La combinación de varios modelos de vidrio junto con otras funciones tecnológicas y financieras relevantes se puede utilizar en la optimización de seis sigma .
{{cite journal}}: Falta o está vacío |title=( ayuda ) ; Z. Tech. Phys. (7): 105, 260. 1926. {{cite journal}}: Faltante o vacío |title=( ayuda ) ; "Lehrbuch der technischen Physik", JA Barth-Verlag, Leipzig, 1924, p. 376.