Análisis de componentes principales del kernel.

En el campo de la estadística multivariada , el análisis de componentes principales del kernel (kernel PCA) ^[1] es una extensión del análisis de componentes principales (PCA) que utiliza técnicas de métodos del kernel . Usando un kernel, las operaciones originalmente lineales de PCA se realizan en un espacio de Hilbert del kernel reproductivo .

Antecedentes: PCA lineal

Recuerde que el PCA convencional opera con datos centrados en cero; eso es,

${\displaystyle {\frac {1}{N}}\sum _{i=1}^{N}\mathbf {x} _{i}=\mathbf {0} }$,

donde es una de las observaciones multivariadas. Opera diagonalizando la matriz de covarianza , ${\displaystyle \mathbf {x} _{i}}$ ${\displaystyle N}$

${\displaystyle C={\frac {1}{N}}\sum _{i=1}^{N}\mathbf {x} _{i}\mathbf {x} _{i}^{\top }}$

en otras palabras, da una descomposición propia de la matriz de covarianza:

${\displaystyle \lambda \mathbf {v} =C\mathbf {v} }$

que se puede reescribir como

${\displaystyle \lambda \mathbf {x} _{i}^{\top }\mathbf {v} =\mathbf {x} _{i}^{\top }C\mathbf {v} \quad {\textrm {for}}~i=1,\ldots ,N}$. ^[2]

(Ver también: Matriz de covarianza como operador lineal )

Introducción del Kernel a PCA

Para comprender la utilidad del PCA del núcleo, particularmente para la agrupación, observe que, si bien N puntos, en general, no pueden separarse linealmente en dimensiones, casi siempre pueden separarse linealmente en dimensiones. Es decir, dados N puntos , si los asignamos a un espacio N -dimensional con ${\displaystyle d<N}$ ${\displaystyle d\geq N}$ ${\displaystyle \mathbf {x} _{i}}$

${\displaystyle \Phi (\mathbf {x} _{i})}$dónde , ${\displaystyle \Phi :\mathbb {R} ^{d}\to \mathbb {R} ^{N}}$

es fácil construir un hiperplano que divida los puntos en grupos arbitrarios. Por supuesto, esto crea vectores linealmente independientes, por lo que no hay covarianza sobre la cual realizar la descomposición propia explícitamente como lo haríamos en PCA lineal. ${\displaystyle \Phi }$

En cambio, en el kernel PCA, se "elige" una función arbitraria y no trivial que nunca se calcula explícitamente, lo que permite la posibilidad de utilizar funciones de dimensiones muy altas si nunca tenemos que evaluar los datos en ese espacio. Como generalmente intentamos evitar trabajar en el espacio, al que llamaremos 'espacio de características', podemos crear el kernel N-by-N. ${\displaystyle \Phi }$ ${\displaystyle \Phi }$ ${\displaystyle \Phi }$

${\displaystyle K=k(\mathbf {x} ,\mathbf {y} )=(\Phi (\mathbf {x} ),\Phi (\mathbf {y} ))=\Phi (\mathbf {x} )^{T}\Phi (\mathbf {y} )}$

que representa el espacio del producto interno (ver matriz de Gramian ) del espacio de características que de otro modo sería intratable. La forma dual que surge en la creación de un núcleo nos permite formular matemáticamente una versión de PCA en la que nunca resolvemos los vectores propios y los valores propios de la matriz de covarianza en el espacio (ver Truco del núcleo ). Los N elementos en cada columna de K representan el producto escalar de un punto de los datos transformados con respecto a todos los puntos transformados (N puntos). En el siguiente ejemplo se muestran algunos núcleos conocidos. ${\displaystyle \Phi (\mathbf {x} )}$

Because we are never working directly in the feature space, the kernel-formulation of PCA is restricted in that it computes not the principal components themselves, but the projections of our data onto those components. To evaluate the projection from a point in the feature space ${\displaystyle \Phi (\mathbf {x} )}$ onto the kth principal component ${\displaystyle V^{k}}$ (where superscript k means the component k, not powers of k)

${\displaystyle {V^{k}}^{T}\Phi (\mathbf {x} )=\left(\sum _{i=1}^{N}\mathbf {a} _{i}^{k}\Phi (\mathbf {x} _{i})\right)^{T}\Phi (\mathbf {x} )}$

We note that ${\displaystyle \Phi (\mathbf {x} _{i})^{T}\Phi (\mathbf {x} )}$ denotes dot product, which is simply the elements of the kernel ${\displaystyle K}$. It seems all that's left is to calculate and normalize the ${\displaystyle \mathbf {a} _{i}^{k}}$, which can be done by solving the eigenvector equation

${\displaystyle N\lambda \mathbf {a} =K\mathbf {a} }$

where ${\displaystyle N}$ is the number of data points in the set, and ${\displaystyle \lambda }$ and ${\displaystyle \mathbf {a} }$ are the eigenvalues and eigenvectors of ${\displaystyle K}$. Then to normalize the eigenvectors ${\displaystyle \mathbf {a} ^{k}}$, we require that

${\displaystyle 1=(V^{k})^{T}V^{k}}$

Care must be taken regarding the fact that, whether or not ${\displaystyle x}$ has zero-mean in its original space, it is not guaranteed to be centered in the feature space (which we never compute explicitly). Since centered data is required to perform an effective principal component analysis, we 'centralize' ${\displaystyle K}$ to become ${\displaystyle K'}$

${\displaystyle K'=K-\mathbf {1_{N}} K-K\mathbf {1_{N}} +\mathbf {1_{N}} K\mathbf {1_{N}} }$

where ${\displaystyle \mathbf {1_{N}} }$ denotes a N-by-N matrix for which each element takes value ${\displaystyle 1/N}$. We use ${\displaystyle K'}$ to perform the kernel PCA algorithm described above.

One caveat of kernel PCA should be illustrated here. In linear PCA, we can use the eigenvalues to rank the eigenvectors based on how much of the variation of the data is captured by each principal component. This is useful for data dimensionality reduction and it could also be applied to KPCA. However, in practice there are cases that all variations of the data are same. This is typically caused by a wrong choice of kernel scale.

Large datasets

In practice, a large data set leads to a large K, and storing K may become a problem. One way to deal with this is to perform clustering on the dataset, and populate the kernel with the means of those clusters. Since even this method may yield a relatively large K, it is common to compute only the top P eigenvalues and eigenvectors of the eigenvalues are calculated in this way.

Example

Input points before kernel PCA

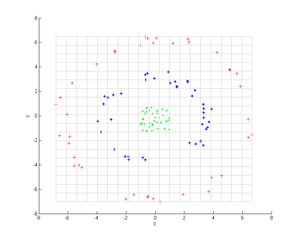
Consider three concentric clouds of points (shown); we wish to use kernel PCA to identify these groups. The color of the points does not represent information involved in the algorithm, but only shows how the transformation relocates the data points.

First, consider the kernel

${\displaystyle k({\boldsymbol {x}},{\boldsymbol {y}})=({\boldsymbol {x}}^{\mathrm {T} }{\boldsymbol {y}}+1)^{2}}$

Applying this to kernel PCA yields the next image.

Output after kernel PCA with ${\displaystyle k({\boldsymbol {x}},{\boldsymbol {y}})=({\boldsymbol {x}}^{\mathrm {T} }{\boldsymbol {y}}+1)^{2}}$. The three groups are distinguishable using the first component only.

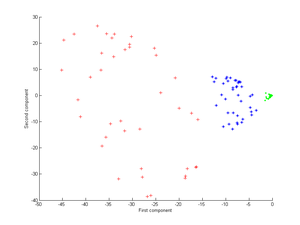
Now consider a Gaussian kernel:

${\displaystyle k({\boldsymbol {x}},{\boldsymbol {y}})=e^{\frac {-||{\boldsymbol {x}}-{\boldsymbol {y}}||^{2}}{2\sigma ^{2}}},}$

That is, this kernel is a measure of closeness, equal to 1 when the points coincide and equal to 0 at infinity.

Output after kernel PCA, with a Gaussian kernel.

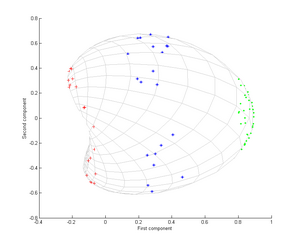
Tenga en cuenta en particular que el primer componente principal es suficiente para distinguir los tres grupos diferentes, lo cual es imposible usando solo PCA lineal, porque el PCA lineal opera solo en el espacio dado (en este caso bidimensional), en el que estas nubes de puntos concéntricos están no linealmente separable.

Aplicaciones

Se ha demostrado que Kernel PCA es útil para la detección de novedades ^[3] y la eliminación de ruido de imágenes. ^[4]

Ver también

• Análisis de conglomerados
• Reducción de dimensionalidad no lineal.
• Agrupación espectral

Referencias

1. Schölkopf, Bernhard; Smola, Alex; Müller, Klaus-Robert (1998). "Análisis de componentes no lineales como un problema de valores propios del kernel". Computación neuronal . 10 (5): 1299-1319. CiteSeerX  10.1.1.100.3636 . doi :10.1162/089976698300017467. S2CID  6674407.
2. Scholkopf, Bernhard; Smola, Alejandro; Müller, Klaus-Robert (diciembre de 1996). Análisis de componentes no lineales como problema de valores propios del kernel (PDF) (Reporte técnico). Max-Planck-Institut für biologische Kybernetik. 44.
3. Hoffmann, Heiko (2007). "Kernel PCA para la detección de novedades". Reconocimiento de patrones . 40 (3): 863–874. doi :10.1016/j.patcog.2006.07.009.
4. Kernel PCA y eliminación de ruido en espacios destacados. NIPS, 1999