La regla del fin del mundo

La regla del día del juicio final , algoritmo del día del juicio final o método del día del juicio final es un algoritmo de determinación del día de la semana para una fecha dada. Proporciona un calendario perpetuo porque el calendario gregoriano se mueve en ciclos de 400 años. El algoritmo para el cálculo mental fue ideado por John Conway en 1973, ^[1]^[2] inspirándose en el algoritmo del calendario perpetuo de Lewis Carroll . ^[3]^[4]^[5] Aprovecha que cada año tiene un cierto día de la semana en el que caen ciertas fechas fáciles de recordar, llamadas días del juicio final ; por ejemplo, el último día de febrero, el 4 de abril (4/4), el 6 de junio (6/6), el 8 de agosto (8/8), el 10 de octubre (10/10) y el 12 de diciembre (12/12) ocurren todos en el mismo día de la semana en cualquier año.

La aplicación del algoritmo del día del juicio final implica tres pasos: determinación del día de anclaje para el siglo, cálculo del día de anclaje para el año a partir del del siglo y selección de la fecha más cercana de las que siempre caen en el día del juicio final, por ejemplo, 4/4 y 6/6, y recuento del número de días ( módulo 7 ) entre esa fecha y la fecha en cuestión para llegar al día de la semana. La técnica se aplica tanto al calendario gregoriano como al calendario juliano , aunque sus días del juicio final suelen ser días diferentes de la semana.

El algoritmo es lo suficientemente simple como para que pueda calcularse mentalmente. Por lo general, Conway podía dar la respuesta correcta en menos de dos segundos. Para mejorar su velocidad, practicaba sus cálculos calendáricos en su computadora, que estaba programada para hacerle preguntas con fechas aleatorias cada vez que se conectaba. ^[6]

Días de anclaje para algunos años contemporáneos

El día de anclaje de Doomsday para el año en curso en el calendario gregoriano (2024) es el jueves. Para otros años contemporáneos:

La tabla se completa de forma horizontal, saltándose una columna por cada año bisiesto. Esta tabla se completa cada 28 años, excepto en el calendario gregoriano en los años que son múltiplos de 100 (como 1800, 1900 y 2100, que no son bisiestos) y que no son también múltiplos de 400 (como 2000, que sigue siendo bisiesto). El ciclo completo es de 28 años (1461 semanas) en el calendario juliano y de 400 años (20 871 semanas) en el calendario gregoriano.

Fechas memorables que siempre caen en el Día del Juicio Final

Se puede encontrar el día de la semana de una fecha determinada del calendario utilizando como punto de referencia un día del juicio final cercano. Para ayudar con esto, la siguiente es una lista de fechas fáciles de recordar para cada mes que siempre coinciden con el día del juicio final.

El último día de febrero es siempre un día del juicio final. En el caso de enero, el 3 de enero es un día del juicio final en los años comunes y el 4 de enero un día del juicio final en los años bisiestos, que se puede recordar como "el 3.º durante 3 años en 4, y el 4.º en el 4.º año". En el caso de marzo, se puede recordar el Día Pi o " Marzo 0 ", este último haciendo referencia al día anterior al 1 de marzo, es decir, el último día de febrero.

Para los meses de abril a diciembre, los meses pares están cubiertos por las fechas dobles 4/4, 6/6, 8/8, 10/10 y 12/12, todas las cuales caen en el día del juicio final. Los meses impares se pueden recordar con la regla mnemotécnica "Trabajo de 9 a 5 en el 7-11 ", es decir, 9/5, 7/11 y también 5/9 y 11/7, son todos días del juicio final (esto es cierto tanto para las convenciones de día/mes como de mes/día). ^[7]

Varias fechas conocidas, como el Día de la Independencia en Estados Unidos , el Día de San Valentín en años comunes , también caen en días del juicio final todos los años. El cuadro a continuación incluye solo las reglas mnemotécnicas que se mencionan en las fuentes mencionadas.

Dado que el día del juicio final de un año determinado está directamente relacionado con los días de la semana de las fechas del período de marzo a febrero del año siguiente, es necesario distinguir entre años comunes y años bisiestos para enero y febrero del mismo año.

Ejemplo

Para saber qué día de la semana es el día de Navidad de 2021, procede de la siguiente manera: en el año 2021, el día del juicio final es el domingo. Dado que el 12 de diciembre es un día del juicio final, el 25 de diciembre, al ser trece días después (dos semanas menos un día), cayó en sábado. El día de Navidad es siempre el día de la semana anterior al día del juicio final. Además, el 4 de julio ( Día de la Independencia de EE. UU. ) siempre es el mismo día de la semana que un día del juicio final, al igual que Halloween (31 de octubre), el Día de Pi (14 de marzo) y el 26 de diciembre ( Boxing Day ).

Nombres de días de la semana mnemotécnicos

Dado que este algoritmo implica tratar los días de la semana como números módulo 7, John Conway sugirió pensar en los días de la semana como "Noneday" o "Sansday" (para el domingo), "Oneday", "Twosday", "Treblesday", "Foursday", "Fiveday" y "Six-a-day" para recordar la relación número-día de la semana sin necesidad de contarlos mentalmente. ^[10]

Hay algunos idiomas, como las lenguas eslavas , el chino , el estonio , el griego , el portugués , el gallego y el hebreo , que basan algunos de los nombres de los días de la semana en su orden posicional . El eslavo, el chino y el estonio concuerdan con la tabla anterior; los demás idiomas mencionados cuentan a partir del domingo como día uno.

Encontrar el día del ancla de un año

En primer lugar, tomemos el día de referencia del siglo. A los efectos de la regla del fin del mundo, un siglo comienza con '00 y termina con '99. La siguiente tabla muestra el día de referencia de los siglos 1600–1699, 1700–1799, 1800–1899, 1900–1999, 2000–2099, 2100–2199 y 2200–2299.

Para el calendario gregoriano:

Fórmula matemática

5 \times (c mod 4) mod 7 +

martes = ancla.

Algorítmico

Sea

r = c mod 4

r = 0

entonces ancla = martes

r = 1

entonces ancla = domingo

r = 2

entonces ancla = viernes

r = 3

entonces ancla = miércoles

Para el calendario juliano:

6 c mod 7 +

domingo = ancla.

Nota: . $c={\biggl \lfloor }{{\text{año}} \más de 100}{\biggr \rfloor }$

A continuación, busque el día de referencia del año. Para lograrlo, según Conway: ^[11]

Divida los dos últimos dígitos del año (llamémoslo $y$ ) por 12 y sea $a$ el mínimo del cociente .
Sea $b$ el resto del mismo cociente.
Divida ese resto por 4 y sea $c$ el mínimo del cociente.
Sea $d$ la suma de los tres números ( $d = a + b + c$ ). (Aquí también es posible dividir por siete y tomar el resto. Este número es equivalente, como debe ser, a $y$ más el mínimo de $y$ dividido por cuatro.)
Cuente hacia adelante el número especificado de días ( $d$ o el resto de $.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}⁠d/7)$ desde el día del ancla hasta obtener el del año.

{\begin{matrix}\left({\left\lfloor {\frac {y}{12}}\right\rfloor +y{\bmod {1}}2+\left\lfloor {\frac {y{\bmod {1}}2}{4}}\right\rfloor }\right){\bmod {7}}+{\rm {{ancla}={\rm {Día del juicio final}}}}\end{matrix}}

Para el año 1966 del siglo XX, por ejemplo:

{\begin{matrix}\left({\left\lfloor {\frac {66}{12}}\right\rfloor +66{\bmod {1}}2+\left\lfloor {\frac {66{\bmod {1}}2}{4}}\right\rfloor }\right){\bmod {7}}+{\rm {Wednesday}}&=&\left(5+6+1\right){\bmod {7}}+{\rm {Wednesday}}\\\ &=&{\rm {Monday}}\end{matrix}}

Como se describe en el punto 4 anterior, esto es equivalente a:

{\begin{matrix}\left({66+\left\lfloor {\frac {66}{4}}\right\rfloor }\right){\bmod {7}}+{\rm {Wednesday}}&=&\left(66+16\right){\bmod {7}}+{\rm {Wednesday}}\\\ &=&{\rm {Monday}}\end{matrix}}

Así pues, el día del juicio final de 1966 cayó en lunes.

De manera similar, el día del juicio final en 2005 será un lunes:

\left({\left\lfloor {\frac {5}{12}}\right\rfloor +5{\bmod {1}}2+\left\lfloor {\frac {5{\bmod {1}}2}{4}}\right\rfloor }\right){\bmod {7}}+{\rm {{Tuesday}={\rm {Monday}}}}

¿Por qué funciona?

El cálculo del día de anclaje del día del juicio final consiste en calcular efectivamente el número de días entre cualquier fecha dada en el año base y la misma fecha en el año actual, y luego tomar el resto módulo 7. Cuando ambas fechas son posteriores al día bisiesto (si lo hay), la diferencia es solo $365 y + ⁠ y / 4 ⁠$ (redondeado hacia abajo). Pero 365 es igual a 52 × 7 + 1, por lo que después de tomar el resto obtenemos solo

\left(y+\left\lfloor {\frac {y}{4}}\right\rfloor \right){\bmod {7}}.

Esto proporciona una fórmula más simple si uno se siente cómodo dividiendo valores grandes de $y$ por 4 y 7. Por ejemplo, podemos calcular

\left(66+\left\lfloor {\frac {66}{4}}\right\rfloor \right){\bmod {7}}=(66+16){\bmod {7}}=82{\bmod {7}}=5

lo que da la misma respuesta que en el ejemplo anterior.

El resultado 12 es que el patrón de casi se repite cada 12 años. Después de 12 años, obtenemos . Si reemplazamos $y$ por $y$ $mod 12$ , estamos desperdiciando este día adicional; pero al agregarlo nuevamente compensamos este error y obtenemos la fórmula final. ${\bigl (}y+{\bigl \lfloor }{\tfrac {y}{4}}{\bigr \rfloor }{\bigr )}{\bmod {7}}$ ${\bigl (}12+{\tfrac {12}{4}}{\bigr )}{\bmod {7}}=15{\bmod {7}}=1$ ${\bigl \lfloor }{\tfrac {y}{12}}{\bigr \rfloor }$

Para calcular el día de anclaje gregoriano de un siglo: tres “siglos comunes” (cada uno con 24 años bisiestos) son seguidos por un “siglo bisiesto” (con 25 años bisiestos). Un siglo común adelanta el día del juicio final en

(100+24){\bmod {7}}=2+3=5

días (equivalentes a dos días atrás). Un siglo bisiesto adelanta el día del juicio final seis días (equivalentes a un día atrás).

Así que , siglos después , el día del juicio final se adelanta.

\left(5c+{\biggl \lfloor }{c \over 4}{\biggr \rfloor }\right){\bmod {7}}

pero esto es equivalente a

(5(c{\bmod {4}})){\bmod {7}}

Cuatro siglos hacen avanzar el día del juicio final

-2-2-2-1=-7,\qquad -7\equiv 0\quad {\pmod {7}}

;

De modo que cuatro siglos forman un ciclo que deja inalterado el día del juicio final (y de ahí el “mod 4” en la fórmula del siglo).

El método "impar + 11"

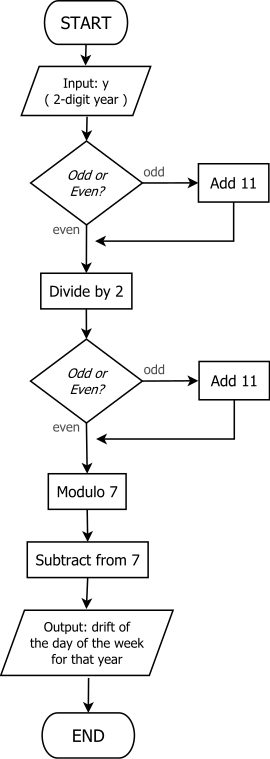
En 2010, Chamberlain Fong y Michael K. Walters descubrieron un método más simple para encontrar el día de referencia del año ^[12] , que fue descrito en su artículo presentado en el 7.º Congreso Internacional de Matemáticas Industriales y Aplicadas (2011). Se denomina método "impar + 11" y es equivalente ^[12] a calcular

\left(y+\left\lfloor {\frac {y}{4}}\right\rfloor \right){\bmod {7}}

Es muy adecuado para el cálculo mental, ya que no requiere división por 4 (o 12) y el procedimiento es fácil de recordar debido al uso repetido de la regla "impar + 11". Además, la suma por 11 es muy fácil de realizar mentalmente en aritmética de base 10 .

Extendiendo esto para obtener el día de ancla, el procedimiento a menudo se describe como la acumulación de un total acumulado $T$ en seis pasos, de la siguiente manera:

Sea $T$ los dos últimos dígitos del año.
Si $T$ es impar, suma 11.
Ahora sea $T = ⁠ yo / 2 ⁠$ .
Si $T$ es impar, suma 11.
Sea ahora $T = 7 - (T mod 7)$ .
Cuente $T$ días hacia adelante a partir del día de anclaje del siglo para obtener el día de anclaje del año.

Aplicando este método al año 2005, por ejemplo, los pasos descritos serían:

$T = 5$
$T = 5 + 11 = 16$ (sumando 11 porque $T$ es impar)
$T = ⁠ 16 / 2 ⁠ = 8$
$T = 8$ (no hacer nada ya que $T$ es par)
$T = 7 - (8 mod 7) = 7 - 1 = 6$
El día del juicio final para el año 2005 = 6 + martes = lunes

La fórmula explícita para el método odd+11 es:

7-\left[{\frac {y+11(y\,{\bmod {2}})}{2}}+11\left({\frac {y+11(y\,{\bmod {2}})}{2}}{\bmod {2}}\right)\right]{\bmod {7}}

Aunque esta expresión parece desalentadora y complicada, en realidad es simple ^[12] debido a una subexpresión común $⁠$ $y + 11(y módulo 2) / 2 ⁠$ que sólo necesita calcularse una vez.

Siempre que se necesita sumar 11, restar 17 da resultados equivalentes. Si bien restar 17 puede parecer más difícil de realizar mentalmente que sumar 11, hay casos en los que restar 17 es más fácil, especialmente cuando el número es un número de dos dígitos que termina en 7 (como 17, 27, 37, ..., 77, 87 y 97).

Correspondencia con carta dominical

El día del juicio final se relaciona con la letra dominical del año de la siguiente manera.

Consulte la tabla a continuación para conocer la letra dominical (DL).

Para el año 2024, la letra dominical es BA + 2 = GF.

Resumen de todos los días del juicio final

* En los años bisiestos, el $n.º$ día del juicio final se da en la semana ISO $n$ . En los años comunes, el día después del $n.º$ día del juicio final se da en la semana $n$ . Por lo tanto, en un año común, el número de semana del día del juicio final es uno menos si es domingo, es decir, en un año común que comienza en viernes (como 2010, 2021 y 2027).

Fórmula informática para el día de anclaje de un año

Para el uso de la computadora, las siguientes fórmulas para el día de ancla de un año son convenientes.

Para el calendario gregoriano:

{\mbox{anchor day}}={\mbox{Tuesday}}+y+\left\lfloor {\frac {y}{4}}\right\rfloor -\left\lfloor {\frac {y}{100}}\right\rfloor +\left\lfloor {\frac {y}{400}}\right\rfloor ={\mbox{Tuesday}}+5\times (y{\bmod {4}})+4\times (y{\bmod {1}}00)+6\times (y{\bmod {4}}00)

Por ejemplo, el día del juicio final de 2009 es el sábado según el calendario gregoriano (el calendario aceptado actualmente), ya que

{\mbox{Saturday (6)}}{\bmod {7}}={\mbox{Tuesday (2)}}+2009+\left\lfloor {\frac {2009}{4}}\right\rfloor -\left\lfloor {\frac {2009}{100}}\right\rfloor +\left\lfloor {\frac {2009}{400}}\right\rfloor

Como otro ejemplo, el día del juicio final de 1946 es el jueves, ya que

{\mbox{Thursday (4)}}{\bmod {7}}={\mbox{Tuesday (2)}}+1946+\left\lfloor {\frac {1946}{4}}\right\rfloor -\left\lfloor {\frac {1946}{100}}\right\rfloor +\left\lfloor {\frac {1946}{400}}\right\rfloor

Para el calendario juliano:

{\mbox{anchor day}}={\mbox{Sunday}}+y+\left\lfloor {\frac {y}{4}}\right\rfloor ={\mbox{Sunday}}+5\times (y{\bmod {4}})+3\times (y{\bmod {7}})

Las fórmulas se aplican también al calendario gregoriano proléptico y al calendario juliano proléptico . Utilizan la función de base y la numeración astronómica para los años antes de Cristo.

A modo de comparación, véase el cálculo de un número de día juliano .

Ciclo de 400 años de días de anclaje

Como en el calendario gregoriano hay 146.097 días, o exactamente 20.871 semanas de siete días, en 400 años, el día de referencia se repite cada cuatro siglos. Por ejemplo, el día de referencia de 1700-1799 es el mismo que el día de referencia de 2100-2199, es decir, el domingo.

El ciclo completo de 400 años de días del juicio final se muestra en la tabla adjunta. Los siglos corresponden al calendario gregoriano y al calendario gregoriano proléptico , a menos que estén marcados con una J para el juliano. Los años bisiestos gregorianos están resaltados.

Los años negativos utilizan la numeración astronómica . El año 25 a. C. es −24, que se muestra en la columna −100J (juliano proléptico) o −100 (gregoriano proléptico), en la fila 76.

Un año bisiesto con el lunes como día del juicio final significa que el domingo es uno de los 97 días que se saltan en la secuencia de 400 años. Por lo tanto, el número total de años con el domingo como día del juicio final es 71 menos el número de años bisiestos con el lunes como día del juicio final, etc. Dado que el lunes como día del juicio final se salta a lo largo del 29 de febrero de 2000, y el patrón de días bisiestos es simétrico con respecto a ese día bisiesto, las frecuencias de días del juicio final por día de la semana (sumando años comunes y bisiestos) son simétricas con respecto al lunes. Las frecuencias de días del juicio final de años bisiestos por día de la semana son simétricas con respecto al día del juicio final de 2000, el martes.

La frecuencia con la que una fecha particular coincide con un día de la semana particular se puede derivar fácilmente de lo anterior (para una fecha del 1 de enero al 28 de febrero, relaciónela con el día del juicio final del año anterior).

Por ejemplo, el 28 de febrero es un día después del día del juicio final del año anterior, por lo que es 58 veces cada uno en martes, jueves y domingo, etc. El 29 de febrero es el día del juicio final de un año bisiesto, por lo que es 15 veces cada uno en lunes y miércoles, etc.

Ciclo de 28 años

En cuanto a la frecuencia de los días del juicio final en un ciclo juliano de 28 años, hay 1 año bisiesto y 3 años comunes para cada día de la semana, estos últimos 6, 17 y 23 años después del primero (por lo que con intervalos de 6, 11, 6 y 5 años; no distribuidos de manera uniforme porque después de 12 años el día se salta en la secuencia de días del juicio final). ^{[ cita requerida ]} El mismo ciclo se aplica para cualquier fecha dada desde el 1 de marzo que cae en un día de la semana en particular.

Para cualquier fecha hasta el 28 de febrero que caiga en un día laborable en particular, los 3 años comunes son 5, 11 y 22 años después del año bisiesto, es decir, con intervalos de 5, 6, 11 y 6 años. Por lo tanto, el ciclo es el mismo, pero con el intervalo de 5 años después en lugar de antes del año bisiesto.

Así, para cualquier fecha excepto el 29 de febrero, los intervalos entre años comunes que caen en un día de la semana en particular son 6, 11, 11. Véase, por ejemplo, en la parte inferior de la página Año común que comienza el lunes los años en el rango 1906-2091.

Que el 29 de febrero caiga en un día laborable determinado solo ocurre uno cada 28 años y, por supuesto, es un año bisiesto.

calendario juliano

Actualmente, el calendario gregoriano se alinea con precisión con eventos astronómicos como los solsticios . En 1582 se instituyó por primera vez esta modificación del calendario juliano . Para corregir la desviación del calendario, se saltaron 10 días, por lo que el día del juicio final se retrasó 10 días (es decir, 3 días): el jueves 4 de octubre (juliano, el día del juicio final es el miércoles) fue seguido por el viernes 15 de octubre (gregoriano, el día del juicio final es el domingo). La tabla incluye años del calendario juliano, pero el algoritmo es solo para el calendario gregoriano y el gregoriano proléptico.

Hay que tener en cuenta que el calendario gregoriano no fue adoptado simultáneamente en todos los países, por lo que durante muchos siglos distintas regiones utilizaron fechas diferentes para el mismo día.

Ejemplos completos

Ejemplo 1 (1985)

Supongamos que queremos saber el día de la semana del 18 de septiembre de 1985. Empezamos con el día de referencia del siglo, el miércoles. A esto, añadimos $a$ , $b$ y $c$ arriba:

$a$ es el piso de $⁠$ $85 / 12 ⁠$ , que es 7.
$b$ es $85 mod 12$ , que es $1$ .
$c$ es el piso de $⁠$ $b / 4 ⁠$ , que es 0.

Esto da como resultado $a + b + c = 8.$ Si contamos 8 días a partir del miércoles, llegamos al jueves, que es el día del juicio final en 1985. (Usando números: en aritmética módulo 7, 8 es congruente con 1. Debido a que el día de anclaje del siglo es el miércoles (índice 3), y 3 + 1 = 4, el día del juicio final en 1985 fue el jueves (índice 4).) Ahora comparamos el 18 de septiembre con un día del juicio final cercano, el 5 de septiembre. Vemos que el 18 es 13 después del día del juicio final, es decir, un día menos que dos semanas. Por lo tanto, el 18 fue un miércoles (el día anterior al jueves). (Usando números: en aritmética módulo 7, 13 es congruente con 6 o, más sucintamente, −1. Por lo tanto, le quitamos uno al día del juicio final, el jueves, para encontrar que el 18 de septiembre de 1985 fue un miércoles.)

Ejemplo 2 (otros siglos)

Supongamos que queremos encontrar el día de la semana en que estalló la Guerra Civil estadounidense en Fort Sumter , que fue el 12 de abril de 1861. El día del ancla para el siglo fue 94 días después del martes o, en otras palabras, el viernes (calculado como $18 \times 5 + ⌊ ⁠ 18 / 4 ⁠ ⌋$ ; o simplemente mira el gráfico, arriba, que enumera los días de anclaje del siglo). Los dígitos 61 dieron un desplazamiento de seis días, por lo que el día del juicio final fue el jueves. Por lo tanto, el 4 de abril fue jueves, por lo que el 12 de abril, ocho días después, fue viernes.

Véase también

Fecha ordinal
Computus – Algoritmo de Gauss para el cálculo de la fecha de Pascua
Congruencia de Zeller : Un algoritmo (1882) para calcular el día de la semana para cualquier fecha del calendario juliano o gregoriano.
Cálculo mental

Referencias

^ John Horton Conway, "Mañana es el día después del juicio final" (PDF) . Eureka. Octubre de 1973. págs. 28-32.
^ Richard Guy, John Horton Conway, Elwyn Berlekamp: "Winning Ways: Para sus juegos matemáticos, Volumen 2: Juegos en particular", páginas 795–797, Academic Press, Londres, 1982, ISBN 0-12-091102-7 .
^ Lewis Carroll, "Cómo encontrar el día de la semana para una fecha determinada", Nature , 31 de marzo de 1887. doi :10.1038/035517a0
^ Martin Gardner, El universo en un pañuelo: recreaciones matemáticas, juegos, rompecabezas y juegos de palabras de Lewis Carroll , páginas 24-26, Springer-Verlag, 1996.
^ "¿Qué día es el día del juicio final?". Mes de la concienciación sobre las matemáticas. Abril de 2014.
^ Alpert, Mark (1 de abril de 1999). «Not Just Fun and Games» (No solo diversión y juegos). Scientific American . Consultado el 18 de abril de 2024 .
^ abcde Torrence, Bruce; Torrence, Eve . «John H. Conway - Doomsday, parte 1». YouTube . Asociación Matemática de Estados Unidos. Archivado desde el original el 21 de diciembre de 2021. Consultado el 14 de abril de 2020 .
^ "El algoritmo del fin del mundo - Numberphile". YouTube . Consultado el 9 de julio de 2023 .
^ ab Limeback, Rudy (3 de enero de 2017). «Algoritmo del fin del mundo» . Consultado el 27 de mayo de 2017 .
^ "¿En qué día de la semana es Navidad? Utilice la regla del fin del mundo". The Irish Times . Consultado el 20 de julio de 2022 .
^ John Horton Conway, "Mañana es el día después del día del juicio final" (PDF) . Eureka. Octubre de 1973. págs. 29-30. Cada año ordinario tiene su día del juicio final 1 día después que el año anterior, y cada año bisiesto, 2 días después. De ello se deduce que, dentro de un siglo dado, una docena de años adelanta el día del juicio final en 12 + 3 = 15 días = 1 día. ("Una docena de años no es más que un día"). De modo que añadimos al día del juicio final del año del siglo el número de docenas de años posteriores, el resto y el número de cuatros del resto.
^ abc Chamberlain Fong, Michael K. Walters: "Métodos para acelerar el algoritmo del fin del mundo de Conway (parte 2)", 7º Congreso Internacional de Matemáticas Industriales y Aplicadas (2011).

Enlaces externos

Wikimedia Commons alberga una categoría multimedia sobre La regla del fin del mundo.

Enciclopedia de cálculo de días laborables de Hans-Christian Solka, 2010
Récords mundiales de cálculo mental del día de la semana en el calendario gregoriano
Récords nacionales para encontrar fechas del calendario
Fechas del Calendario Mental de la Clasificación Mundial de Memoriad (todas las competiciones combinadas)
Algoritmo del fin del mundo
Encontrar el día de la semana
Poema que explica la regla del Juicio Final en Wayback Machine (archivado el 18 de octubre de 2006)
Calculadora del fin del mundo en timeanddate