En electrónica , una red de dos puertos (una especie de red de cuatro terminales o cuadripolo ) es una red eléctrica (es decir, un circuito) o dispositivo con dos pares de terminales para conectarse a circuitos externos. Dos terminales constituyen un puerto si las corrientes aplicadas a ellos satisfacen el requisito esencial conocido como condición de puerto: la corriente que entra en un terminal debe ser igual a la corriente que emerge del otro terminal en el mismo puerto. [1] [2] Los puertos constituyen interfaces donde la red se conecta a otras redes, los puntos donde se aplican señales o se toman salidas. En una red de dos puertos, a menudo el puerto 1 se considera el puerto de entrada y el puerto 2 se considera el puerto de salida.
Se utiliza comúnmente en el análisis de circuitos matemáticos .
El modelo de red de dos puertos se utiliza en técnicas de análisis matemático de circuitos para aislar partes de circuitos más grandes. Una red de dos puertos se considera como una " caja negra " con sus propiedades especificadas por una matriz de números. Esto permite calcular fácilmente la respuesta de la red a las señales aplicadas a los puertos, sin tener que resolver todos los voltajes y corrientes internos de la red. También permite comparar fácilmente circuitos o dispositivos similares. Por ejemplo, los transistores a menudo se consideran de dos puertos, caracterizados por sus parámetros h (ver más abajo) que son enumerados por el fabricante. Cualquier circuito lineal con cuatro terminales puede considerarse una red de dos puertos siempre que no contenga una fuente independiente y satisfaga las condiciones del puerto.
Ejemplos de circuitos analizados como de dos puertos son filtros , redes de adaptación , líneas de transmisión , transformadores y modelos de pequeña señal para transistores (como el modelo híbrido-pi ). El análisis de redes pasivas de dos puertos es una consecuencia de los teoremas de reciprocidad derivados por primera vez por Lorentz. [3]
En los modelos matemáticos de dos puertos, la red se describe mediante una matriz cuadrada de 2 por 2 de números complejos . Los modelos comunes que se utilizan se denominan parámetros z , parámetros y , parámetros h , parámetros g y parámetros ABCD , cada uno de los cuales se describe individualmente a continuación. Todos ellos se limitan a redes lineales , ya que un supuesto subyacente de su derivación es que cualquier condición de circuito dada es una superposición lineal de varias condiciones de cortocircuito y circuito abierto. Por lo general, se expresan en notación matricial y establecen relaciones entre las variables.
que se muestran en la figura 1. La diferencia entre los distintos modelos radica en cuáles de estas variables se consideran variables independientes . Estas variables de corriente y voltaje son más útiles en frecuencias bajas a moderadas. En frecuencias altas (por ejemplo, frecuencias de microondas), el uso de variables de potencia y energía es más apropiado, y el enfoque de corriente-voltaje de dos puertos se reemplaza por un enfoque basado en parámetros de dispersión .
Existen ciertas propiedades de los dos puertos que se dan con frecuencia en redes prácticas y que se pueden utilizar para simplificar enormemente el análisis. Entre ellas se incluyen:
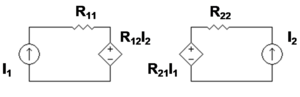
dónde
Todos los parámetros z tienen dimensiones en ohmios .
Para redes recíprocas z 12 = z 21 . Para redes simétricas z 11 = z 22 . Para redes recíprocas sin pérdidas todos los z mn son puramente imaginarios. [7]
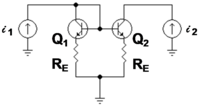

La figura 3 muestra un espejo de corriente bipolar con resistencias de emisor para aumentar su resistencia de salida. [nb 1] El transistor Q 1 está conectado a un diodo , es decir, su voltaje colector-base es cero. La figura 4 muestra el circuito de pequeña señal equivalente a la figura 3. El transistor Q 1 está representado por su resistencia de emisor r E :
una simplificación que es posible porque la fuente de corriente dependiente en el modelo híbrido-pi para Q 1 consume la misma corriente que una resistencia 1 / g m conectada a través de r π . El segundo transistor Q 2 está representado por su modelo híbrido-pi . La Tabla 1 a continuación muestra las expresiones de parámetros z que hacen que el circuito equivalente a z de la Figura 2 sea eléctricamente equivalente al circuito de pequeña señal de la Figura 4.
La retroalimentación negativa introducida por las resistencias R E se puede ver en estos parámetros. Por ejemplo, cuando se utiliza como carga activa en un amplificador diferencial, I 1 ≈ − I 2 , lo que hace que la impedancia de salida del espejo sea aproximadamente
en comparación con solo r O sin retroalimentación (es decir, con R E = 0 Ω). Al mismo tiempo, la impedancia en el lado de referencia del espejo es aproximadamente
Solo un valor moderado, pero aún mayor que r E sin retroalimentación. En la aplicación del amplificador diferencial, una resistencia de salida grande aumenta la ganancia del modo diferencial, algo bueno, y una resistencia de entrada de espejo pequeña es deseable para evitar el efecto Miller .
dónde
Todos los parámetros Y tienen dimensiones de siemens .
Para redes recíprocas y 12 = y 21 . Para redes simétricas y 11 = y 22 . Para redes recíprocas sin pérdidas, todos los y mn son puramente imaginarios. [7]
dónde
Este circuito suele seleccionarse cuando se desea un amplificador de corriente en la salida. Las resistencias que se muestran en el diagrama pueden ser impedancias generales.
Los parámetros h fuera de la diagonal son adimensionales , mientras que los miembros diagonales tienen dimensiones recíprocas entre sí.
Para redes recíprocas h 12 = – h 21 . Para redes simétricas h 11 h 22 – h 12 h 21 = 1 . Para redes recíprocas sin pérdidas h 12 y h 21 son reales, mientras que h 11 y h 22 son puramente imaginarias.
Nota: Las fórmulas tabuladas en la Tabla 2 hacen que el circuito h -equivalente del transistor de la Figura 6 concuerde con su modelo híbrido-pi de baja frecuencia y señal pequeña de la Figura 7. Notación: r π es la resistencia de base del transistor, r O es la resistencia de salida y g m es la transconductancia mutua. El signo negativo para h 21 refleja la convención de que I 1 , I 2 son positivos cuando se dirigen al puerto de dos. Un valor distinto de cero para h 12 significa que el voltaje de salida afecta el voltaje de entrada, es decir, este amplificador es bilateral . Si h 12 = 0 , el amplificador es unilateral .
Los parámetros h se denominaron inicialmente parámetros serie-paralelo . El término híbrido para describir estos parámetros fue acuñado por DA Alsberg en 1953 en "Metrología de transistores". [8] En 1954, un comité conjunto del IRE y la AIEE adoptó el término parámetros h y recomendó que estos se convirtieran en el método estándar para probar y caracterizar transistores porque eran "peculiarmente adaptables a las características físicas de los transistores". [9] En 1956, la recomendación se convirtió en un estándar emitido; 56 IRE 28.S2. Tras la fusión de estas dos organizaciones como IEEE , el estándar se convirtió en Std 218-1956 y se reafirmó en 1980, pero ahora ha sido retirado. [10]
dónde
A menudo, se selecciona este circuito cuando se desea un amplificador de voltaje en la salida. Los parámetros g fuera de la diagonal son adimensionales, mientras que los elementos diagonales tienen dimensiones recíprocas entre sí. Las resistencias que se muestran en el diagrama pueden ser impedancias generales.
Nota: Las fórmulas tabuladas en la Tabla 3 hacen que el circuito equivalente a g del transistor de la Figura 8 concuerde con su modelo híbrido-pi de baja frecuencia y señal pequeña de la Figura 9. Notación: r π es la resistencia de base del transistor, r O es la resistencia de salida y g m es la transconductancia mutua. El signo negativo para g 12 refleja la convención de que I 1 , I 2 son positivos cuando se dirigen al puerto de dos. Un valor distinto de cero para g 12 significa que la corriente de salida afecta a la corriente de entrada, es decir, este amplificador es bilateral . Si g 12 = 0 , el amplificador es unilateral .
Los parámetros ABCD se conocen como parámetros de cadena, cascada o transmisión. Existen varias definiciones de parámetros ABCD , la más común es [11] [12]
Nota: Algunos autores optaron por invertir la dirección indicada de I 2 y suprimir el signo negativo en I 2 .
dónde
Para redes recíprocas AD – BC = 1. Para redes simétricas A = D. Para redes que son recíprocas y sin pérdidas, A y D son puramente reales mientras que B y C son puramente imaginarias. [6]
Se prefiere esta representación porque cuando los parámetros se utilizan para representar una cascada de dos puertos, las matrices se escriben en el mismo orden en que se dibujaría un diagrama de red, es decir, de izquierda a derecha. Sin embargo, también se utiliza una definición variante, [13]
dónde
El signo negativo de – I 2 surge para hacer que la corriente de salida de una etapa en cascada (tal como aparece en la matriz) sea igual a la corriente de entrada de la siguiente. Sin el signo menos, las dos corrientes tendrían sentidos opuestos porque la dirección positiva de la corriente, por convención, se toma como la corriente que ingresa al puerto. En consecuencia, el vector de matriz de voltaje/corriente de entrada se puede reemplazar directamente con la ecuación matricial de la etapa en cascada anterior para formar una matriz A'B'C'D' combinada .
La terminología de representar los parámetros ABCD como una matriz de elementos designados a 11 etc. adoptada por algunos autores [14] y los parámetros A'B'C'D' inversos como una matriz de elementos designados b 11 etc. se utilizan aquí tanto por brevedad como para evitar confusiones con elementos del circuito.
La siguiente tabla enumera los parámetros ABCD y ABCD inverso para algunos elementos de red simples.

Los parámetros anteriores se definen en términos de voltajes y corrientes en los puertos. Los parámetros S son diferentes y se definen en términos de ondas incidentes y reflejadas en los puertos. Los parámetros S se utilizan principalmente en frecuencias de microondas y UHF donde resulta difícil medir voltajes y corrientes directamente. Por otro lado, la potencia incidente y reflejada son fáciles de medir utilizando acopladores direccionales . La definición es [16]
donde a k son las ondas incidentes y b k son las ondas reflejadas en el puerto k . Es convencional definir a k y b k en términos de la raíz cuadrada de la potencia. En consecuencia, existe una relación con los voltajes de onda (consulte el artículo principal para obtener más detalles). [17]
Para redes recíprocas S 12 = S 21 . Para redes simétricas S 11 = S 22 . Para redes antimétricas S 11 = – S 22 . [18] Para redes recíprocas sin pérdidas y [19]
Los parámetros de transferencia de dispersión, al igual que los parámetros de dispersión, se definen en términos de ondas incidentes y reflejadas. La diferencia es que los parámetros T relacionan las ondas en el puerto 1 con las ondas en el puerto 2, mientras que los parámetros S relacionan las ondas reflejadas con las ondas incidentes. En este sentido, los parámetros T cumplen la misma función que los parámetros ABCD y permiten calcular los parámetros T de las redes en cascada mediante la multiplicación de matrices de las redes componentes. Los parámetros T , al igual que los parámetros ABCD , también pueden denominarse parámetros de transmisión. La definición es [16] [20]
Los parámetros T no son tan fáciles de medir directamente como los parámetros S. Sin embargo, los parámetros S se pueden convertir fácilmente en parámetros T ; consulte el artículo principal para obtener más detalles. [21]
Cuando se conectan dos o más redes de dos puertos, los parámetros de los dos puertos de la red combinada se pueden encontrar realizando álgebra matricial en las matrices de parámetros para los dos puertos componentes. La operación matricial se puede hacer particularmente simple con una elección apropiada de los parámetros de los dos puertos para que coincidan con la forma de conexión de los dos puertos. Por ejemplo, los parámetros z son mejores para los puertos conectados en serie.
Las reglas de combinación deben aplicarse con cuidado. Algunas conexiones (cuando se unen potenciales diferentes) hacen que la condición del puerto se invalide y la regla de combinación ya no se aplique. Se puede utilizar una prueba de Brune para verificar la admisibilidad de la combinación. Esta dificultad se puede superar colocando transformadores ideales 1:1 en las salidas de los dos puertos del problema. Esto no cambia los parámetros de los dos puertos, pero sí garantiza que seguirán cumpliendo la condición del puerto cuando se interconecten. En las figuras 11 y 12 que aparecen a continuación se muestra un ejemplo de este problema para conexiones serie-serie. [22]
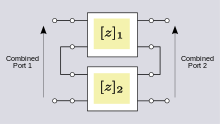
Cuando se conectan dos puertos en una configuración serie-serie como se muestra en la figura 10, la mejor opción de parámetro de dos puertos son los parámetros z . Los parámetros z de la red combinada se encuentran mediante la suma de las matrices de los dos parámetros z individuales . [23] [24]

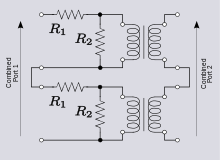
Como se mencionó anteriormente, hay algunas redes que no se prestan directamente a este análisis. [22] Un ejemplo simple es un puerto doble que consta de una red L de resistencias R 1 y R 2 . Los parámetros z para esta red son:
La figura 11 muestra dos redes idénticas conectadas en serie-serie. Los parámetros z totales predichos por la suma de matrices son:
Sin embargo, el análisis directo del circuito combinado muestra que,
La discrepancia se explica al observar que R 1 de los dos puertos inferiores ha sido pasado por alto por el cortocircuito entre dos terminales de los puertos de salida. Esto da como resultado que no fluya corriente a través de un terminal en cada uno de los puertos de entrada de las dos redes individuales. En consecuencia, la condición del puerto se rompe para ambos puertos de entrada de las redes originales, ya que la corriente aún puede fluir hacia el otro terminal. Este problema se puede resolver insertando un transformador ideal en el puerto de salida de al menos una de las redes de dos puertos. Si bien este es un enfoque común en los libros de texto para presentar la teoría de los dos puertos, la viabilidad de usar transformadores es una cuestión que se debe decidir para cada diseño individual.

Cuando se conectan dos puertos en una configuración paralelo-paralelo como se muestra en la figura 13, la mejor opción de parámetro de dos puertos son los parámetros y . Los parámetros y de la red combinada se encuentran mediante la suma de las matrices de los dos parámetros y individuales . [25]

Cuando se conectan dos puertos en una configuración en serie-paralelo como se muestra en la figura 14, la mejor opción de parámetro de dos puertos son los parámetros h . Los parámetros h de la red combinada se obtienen mediante la suma de las matrices de los dos parámetros h individuales . [26]

Cuando se conectan dos puertos en una configuración en serie-paralelo como se muestra en la figura 15, la mejor opción de parámetro de dos puertos son los parámetros g . Los parámetros g de la red combinada se obtienen mediante la suma de las matrices de los dos parámetros g individuales .

Cuando se conectan dos puertos con el puerto de salida del primero conectado al puerto de entrada del segundo (una conexión en cascada), como se muestra en la figura 16, la mejor opción de parámetro de dos puertos son los parámetros ABCD . Los parámetros a de la red combinada se encuentran mediante la multiplicación matricial de las dos matrices de parámetros a individuales. [27]
Una cadena de n puertos de dos vías se puede combinar mediante la multiplicación matricial de las n matrices. Para combinar una cascada de matrices de b parámetros, se vuelven a multiplicar, pero la multiplicación debe realizarse en orden inverso, de modo que:
Supongamos que tenemos una red de dos puertos que consta de una resistencia en serie R seguida de un condensador en derivación C. Podemos modelar toda la red como una cascada de dos redes más simples:
La matriz de transmisión para toda la red [ b ] es simplemente la multiplicación matricial de las matrices de transmisión de los dos elementos de la red:
De este modo:
Donde Δ[ x ] es el determinante de [ x ] .
Ciertos pares de matrices tienen una relación particularmente simple. Los parámetros de admitancia son la matriz inversa de los parámetros de impedancia, los parámetros híbridos inversos son la matriz inversa de los parámetros híbridos y la forma [ b ] de los parámetros ABCD es la matriz inversa de la forma [ a ] . Es decir,
Si bien las redes de dos puertos son muy comunes (por ejemplo, amplificadores y filtros), otras redes eléctricas, como acopladores direccionales y circuladores, tienen más de dos puertos. Las siguientes representaciones también son aplicables a redes con una cantidad arbitraria de puertos:
Por ejemplo, los parámetros de impedancia de tres puertos dan como resultado la siguiente relación:
Sin embargo, las siguientes representaciones están necesariamente limitadas a dispositivos de dos puertos:
Una red de dos puertos tiene cuatro variables, dos de las cuales son independientes. Si uno de los puertos termina con una carga sin fuentes independientes, la carga impone una relación entre el voltaje y la corriente de ese puerto. Se pierde un grado de libertad. El circuito ahora tiene solo un parámetro independiente. El puerto doble se convierte en una impedancia de un puerto para la variable independiente restante.
Por ejemplo, considere los parámetros de impedancia.
Conectar una carga, Z L, al puerto 2 agrega efectivamente la restricción
El signo negativo se debe a que la dirección positiva de I 2 se dirige hacia los dos puertos en lugar de hacia la carga. Las ecuaciones aumentadas se convierten en
La segunda ecuación se puede resolver fácilmente para I 2 como función de I 1 y esa expresión puede reemplazar a I 2 en la primera ecuación dejando a V 1 (y V 2 e I 2 ) como funciones de I 1.
Entonces, en efecto, I 1 ve una impedancia de entrada Z y el efecto de los dos puertos en el circuito de entrada se ha reducido efectivamente a un puerto; es decir, una simple impedancia de dos terminales.