División de polos

La división de polos es un fenómeno que se explota en algunas formas de compensación de frecuencia que se utilizan en un amplificador electrónico . Cuando se introduce un condensador entre los lados de entrada y salida del amplificador con la intención de mover el polo de menor frecuencia (normalmente un polo de entrada) a frecuencias más bajas, la división de polos hace que el polo siguiente en frecuencia (normalmente un polo de salida) se mueva a una frecuencia más alta. Este movimiento de polos aumenta la estabilidad del amplificador y mejora su respuesta de paso a costa de una menor velocidad. ^{[1] [2] [3] [4]}

Ejemplo de división de polos

Figura 1: Amplificador operacional con condensador de compensación C _C entre la entrada y la salida; observe que el amplificador tiene una impedancia de entrada R _i y una impedancia de salida R _o . (edición: esta figura es errónea, ya que los signos + y - deben estar invertidos. Debe haber retroalimentación negativa).

Figura 2: Amplificador operacional con condensador de compensación transformado utilizando el teorema de Miller para reemplazar el condensador de compensación con un condensador de Miller en la entrada y una fuente de corriente dependiente de la frecuencia en la salida. (edición: esta figura es errónea, ya que los signos + y - deben estar invertidos. Debe haber retroalimentación negativa).

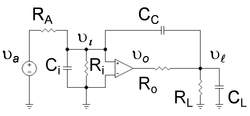
Este ejemplo muestra que la introducción del condensador denominado C _C en el amplificador de la Figura 1 tiene dos resultados: primero, hace que el polo de frecuencia más baja del amplificador se mueva aún más abajo en frecuencia y segundo, hace que el polo más alto se mueva más arriba en frecuencia. ^[5] El amplificador de la Figura 1 tiene un polo de baja frecuencia debido a la resistencia de entrada añadida R _i y la capacitancia C _i , con la constante de tiempo C _i ( R _A || R _i ). Este polo se mueve hacia abajo en frecuencia por el efecto Miller . El amplificador obtiene un polo de salida de alta frecuencia mediante la adición de la resistencia de carga R _L y la capacitancia C _L , con la constante de tiempo C _L ( R _o || R _L ). El movimiento ascendente del polo de alta frecuencia se produce porque el condensador de compensación amplificado por Miller C _C altera la dependencia de la frecuencia del divisor de tensión de salida.

El primer objetivo, mostrar que el polo más bajo se mueve hacia abajo en frecuencia, se establece utilizando el mismo enfoque que el artículo sobre el teorema de Miller . Siguiendo el procedimiento descrito en el artículo sobre el teorema de Miller , el circuito de la Figura 1 se transforma en el de la Figura 2, que es eléctricamente equivalente a la Figura 1. La aplicación de la ley de corriente de Kirchhoff al lado de entrada de la Figura 2 determina el voltaje de entrada al amplificador operacional ideal como una función del voltaje de señal aplicado , es decir, ${\displaystyle \ v_{i}}$ ${\displaystyle \ v_{a}}$

${\displaystyle {\frac {v_{i}}{v_{a}}}={\frac {R_{i}}{R_{i}+R_{A}}}{\frac {1}{1+j\omega (C_{M}+C_{i})(R_{A}\|R_{i})}}\ ,}$

que exhibe una caída con una frecuencia que comienza en f ₁ donde

${\displaystyle {\begin{aligned}f_{1}&={\frac {1}{2\pi (C_{M}+C_{i})(R_{A}\|R_{i})}}\\&={\frac {1}{2\pi \tau _{1}}}\ ,\\\end{aligned}}}$

que introduce la notación para la constante de tiempo del polo más bajo. Esta frecuencia es menor que la frecuencia baja inicial del amplificador, que para C _C = 0 F es . ${\displaystyle \tau _{1}}$ ${\displaystyle {\frac {1}{2\pi C_{i}(R_{A}\|R_{i})}}}$

Pasando al segundo objetivo, que muestra que el polo superior se mueve aún más alto en frecuencia, es necesario observar el lado de salida del circuito, que aporta un segundo factor a la ganancia general y una dependencia adicional de la frecuencia. El voltaje está determinado por la ganancia del amplificador operacional ideal dentro del amplificador como ${\displaystyle \ v_{o}}$

${\displaystyle \ v_{o}=A_{v}v_{i}\ .}$

Usando esta relación y aplicando la ley de corriente de Kirchhoff al lado de salida del circuito, se determina el voltaje de carga en función del voltaje en la entrada del amplificador operacional ideal como: ${\displaystyle v_{\ell }}$ ${\displaystyle \ v_{i}}$

${\displaystyle {\frac {v_{\ell }}{v_{i}}}=A_{v}{\frac {R_{L}}{R_{L}+R_{o}}}\,\!}$ ${\displaystyle \cdot {\frac {1+j\omega C_{C}R_{o}/A_{v}}{1+j\omega (C_{L}+C_{C})(R_{o}\|R_{L})}}\ .}$

Esta expresión se combina con el factor de ganancia encontrado anteriormente para el lado de entrada del circuito para obtener la ganancia general como

${\displaystyle {\frac {v_{\ell }}{v_{a}}}={\frac {v_{\ell }}{v_{i}}}{\frac {v_{i}}{v_{a}}}}$

${\displaystyle =A_{v}{\frac {R_{i}}{R_{i}+R_{A}}}\cdot {\frac {R_{L}}{R_{L}+R_{o}}}\,\!}$ ${\displaystyle \cdot {\frac {1}{1+j\omega (C_{M}+C_{i})(R_{A}\|R_{i})}}\,\!}$ ${\displaystyle \cdot {\frac {1+j\omega C_{C}R_{o}/A_{v}}{1+j\omega (C_{L}+C_{C})(R_{o}\|R_{L})}}\ .}$

Esta fórmula de ganancia parece mostrar una respuesta simple de dos polos con dos constantes de tiempo. (También exhibe un cero en el numerador pero, suponiendo que la ganancia del amplificador A _v es grande, este cero es importante solo en frecuencias demasiado altas para importar en esta discusión, por lo que el numerador puede aproximarse como la unidad). Sin embargo, aunque el amplificador tiene un comportamiento de dos polos, las dos constantes de tiempo son más complicadas de lo que sugiere la expresión anterior porque la capacitancia de Miller contiene una dependencia de frecuencia oculta que no tiene importancia en frecuencias bajas, pero tiene un efecto considerable en frecuencias altas. Es decir, suponiendo que el producto RC de salida, C _L ( R _o || R _L ), corresponde a una frecuencia muy por encima del polo de baja frecuencia, se debe utilizar la forma precisa de la capacitancia de Miller, en lugar de la aproximación de Miller . Según el artículo sobre el efecto Miller , la capacitancia de Miller está dada por

${\displaystyle {\begin{aligned}C_{M}&=C_{C}\left(1-{\frac {v_{\ell }}{v_{i}}}\right)\\&=C_{C}\left(1-A_{v}{\frac {R_{L}}{R_{L}+R_{o}}}{\frac {1+j\omega C_{C}R_{o}/A_{v}}{1+j\omega (C_{L}+C_{C})(R_{o}\|R_{L})}}\right)\ .\\\end{aligned}}}$

(Para una capacitancia de Miller positiva, A _v es negativo). Al sustituir este resultado en la expresión de ganancia y los términos de recopilación, la ganancia se reescribe como:

${\displaystyle {\frac {v_{\ell }}{v_{a}}}=A_{v}{\frac {R_{i}}{R_{i}+R_{A}}}{\frac {R_{L}}{R_{L}+R_{o}}}{\frac {1+j\omega C_{C}R_{o}/A_{v}}{D_{\omega }}}\ ,}$

con D _ω dado por una cuadrática en ω, a saber:

${\displaystyle D_{\omega }\,\!}$ ${\displaystyle =[1+j\omega (C_{L}+C_{C})(R_{o}\|R_{L})]\,\!}$ ${\displaystyle \cdot \ [1+j\omega C_{i}(R_{A}\|R_{i})]\,\!}$ ${\displaystyle \ +j\omega C_{C}(R_{A}\|R_{i})\,\!}$ ${\displaystyle \cdot \left(1-A_{v}{\frac {R_{L}}{R_{L}+R_{O}}}\right)\,\!}$ ${\displaystyle \ +(j\omega )^{2}C_{C}C_{L}(R_{A}\|R_{i})(R_{O}\|R_{L})\ .}$

Toda ecuación cuadrática tiene dos factores, y esta expresión parece más simple si se reescribe como

${\displaystyle \ D_{\omega }=(1+j\omega {\tau }_{1})(1+j\omega {\tau }_{2})}$

${\displaystyle =1+j\omega ({\tau }_{1}+{\tau }_{2}))+(j\omega )^{2}\tau _{1}\tau _{2}\ ,\ }$

donde y son combinaciones de las capacitancias y resistencias en la fórmula para D _ω . ^[6] Corresponden a las constantes de tiempo de los dos polos del amplificador. Una u otra constante de tiempo es la más larga; suponga que es la constante de tiempo más larga, correspondiente al polo más bajo, y suponga >> . (Una buena respuesta al escalón requiere >> . Vea la selección de CC a continuación). ${\displaystyle \tau _{1}}$ ${\displaystyle \tau _{2}}$ ${\displaystyle \tau _{1}}$ ${\displaystyle \tau _{1}}$ ${\displaystyle \tau _{2}}$ ${\displaystyle \tau _{1}}$ ${\displaystyle \tau _{2}}$

A bajas frecuencias cerca del polo más bajo de este amplificador, normalmente el término lineal en ω es más importante que el término cuadrático, por lo que el comportamiento de baja frecuencia de D _ω es:

${\displaystyle {\begin{aligned}\ D_{\omega }&=1+j\omega [(C_{M}+C_{i})(R_{A}\|R_{i})+(C_{L}+C_{C})(R_{o}\|R_{L})]\\&=1+j\omega (\tau _{1}+\tau _{2})\approx 1+j\omega \tau _{1}\ ,\ \\\end{aligned}}}$

donde ahora C _M se redefine utilizando la aproximación de Miller como

${\displaystyle C_{M}=C_{C}\left(1-A_{v}{\frac {R_{L}}{R_{L}+R_{o}}}\right)\ ,}$

que es simplemente la capacitancia de Miller anterior evaluada a bajas frecuencias. Sobre esta base se determina, siempre que >> . Debido a que C _M es grande, la constante de tiempo es mucho mayor que su valor original de C _i ( R _A || R _i ). ^[7] ${\displaystyle \tau _{1}}$ ${\displaystyle \tau _{1}}$ ${\displaystyle \tau _{2}}$ ${\displaystyle {\tau }_{1}}$

A frecuencias altas, el término cuadrático se vuelve importante. Suponiendo que el resultado anterior para es válido, la segunda constante de tiempo, la posición del polo de alta frecuencia, se encuentra a partir del término cuadrático en D _ω como ${\displaystyle \tau _{1}}$

${\displaystyle \tau _{2}={\frac {\tau _{1}\tau _{2}}{\tau _{1}}}\approx {\frac {\tau _{1}\tau _{2}}{\tau _{1}+\tau _{2}}}\ .}$

Sustituyendo en esta expresión el coeficiente cuadrático correspondiente al producto junto con la estimación para , se obtiene una estimación para la posición del segundo polo: ${\displaystyle \tau _{1}\tau _{2}}$ ${\displaystyle \tau _{1}}$

${\displaystyle {\begin{aligned}\tau _{2}&={\frac {(C_{C}C_{L}+C_{L}C_{i}+C_{i}C_{C})(R_{A}\|R_{i})(R_{O}\|R_{L})}{(C_{M}+C_{i})(R_{A}\|R_{i})+(C_{L}+C_{C})(R_{o}\|R_{L})}}\\&\approx {\frac {C_{C}C_{L}+C_{L}C_{i}+C_{i}C_{C}}{C_{M}}}(R_{O}\|R_{L})\ ,\\\end{aligned}}}$

y debido a que C _M es grande, parece reducirse en tamaño desde su valor original C _L ( R _o || R _L ); es decir, el polo superior se ha movido aún más alto en frecuencia debido a C _C . ^[8] ${\displaystyle \tau _{2}}$

En resumen, la introducción del condensador C _C movió el polo bajo hacia abajo y el polo alto hacia arriba, por lo que el término división de polos parece una buena descripción.

Selección de Cdo

Figura 3: Diagrama de Bode idealizado para un diseño de amplificador de dos polos. La ganancia cae desde el primer polo en f ₁ a 20 dB/década hasta el segundo polo en f _2, donde la pendiente aumenta a 40 dB/década.

¿Qué valor es una buena opción para C _C ? Para uso general, el diseño tradicional (a menudo llamado compensación de polo dominante o de polo único ) requiere que la ganancia del amplificador caiga 20 dB/década desde la frecuencia de esquina hasta una ganancia de 0 dB, o incluso menos. ^{[9] [10] Con este diseño, el amplificador es estable y tiene} una respuesta de paso casi óptima incluso como un búfer de voltaje de ganancia unitaria. Una técnica más agresiva es la compensación de dos polos. ^{[11] [12]}

La forma de posicionar f ₂ para obtener el diseño se muestra en la Figura 3. En el polo más bajo f ₁ , el diagrama de ganancia de Bode rompe la pendiente para caer a 20 dB/década. El objetivo es mantener la pendiente de 20 dB/década hasta cero dB, y tomando la relación de la caída deseada en ganancia (en dB) de 20 log ₁₀ A _v al cambio requerido en frecuencia (en una escala de frecuencia logarítmica ^[13] ) de ( log ₁₀ f ₂  − log ₁₀ f ₁ ) = log ₁₀ ( f ₂ / f ₁ ) la pendiente del segmento entre f ₁ y f ₂ es:

Pendiente por década de frecuencia ${\displaystyle =20{\frac {\mathrm {log_{10}} (A_{v})}{\mathrm {log_{10}} (f_{2}/f_{1})}}\ ,}$

que es 20 dB/década siempre que f ₂ = A _v f ₁ . Si f ₂ no es tan grande, la segunda interrupción en el diagrama de Bode que ocurre en el segundo polo interrumpe el diagrama antes de que la ganancia caiga a 0 dB con la consiguiente menor estabilidad y respuesta de paso degradada.

La figura 3 muestra que para obtener la dependencia correcta de la ganancia con respecto a la frecuencia, el segundo polo es al menos un factor A _v más alto en frecuencia que el primer polo. La ganancia se reduce un poco mediante los divisores de voltaje en la entrada y la salida del amplificador, por lo que con correcciones a A _v para los divisores de voltaje en la entrada y la salida, la condición de relación de polos para una buena respuesta al escalón se convierte en:

${\displaystyle {\frac {\tau _{1}}{\tau _{2}}}\approx A_{v}{\frac {R_{i}}{R_{i}+R_{A}}}\cdot {\frac {R_{L}}{R_{L}+R_{o}}}\ ,}$

Figura 4: Capacitancia de Miller a bajas frecuencias C _M (arriba) y capacitor de compensación C _C (abajo) en función de la ganancia utilizando Excel . Las unidades de capacitancia son pF.

Utilizando las aproximaciones para las constantes de tiempo desarrolladas anteriormente,

${\displaystyle {\frac {\tau _{1}}{\tau _{2}}}\approx {\frac {(\tau _{1}+\tau _{2})^{2}}{\tau _{1}\tau _{2}}}\approx A_{v}{\frac {R_{i}}{R_{i}+R_{A}}}\cdot {\frac {R_{L}}{R_{L}+R_{o}}}\ ,}$

o

${\displaystyle {\frac {[(C_{M}+C_{i})(R_{A}\|R_{i})+(C_{L}+C_{C})(R_{o}\|R_{L})]^{2}}{(C_{C}C_{L}+C_{L}C_{i}+C_{i}C_{C})(R_{A}\|R_{i})(R_{O}\|R_{L})}}\,\!}$ ${\displaystyle {\color {White}\cdot }=A_{v}{\frac {R_{i}}{R_{i}+R_{A}}}\cdot {\frac {R_{L}}{R_{L}+R_{o}}}\ ,}$

que proporciona una ecuación cuadrática para determinar un valor apropiado para C _C . La figura 4 muestra un ejemplo que utiliza esta ecuación. Con valores bajos de ganancia, este amplificador de ejemplo satisface la condición de relación polar sin compensación (es decir, en la figura 4, el condensador de compensación C _C es pequeño con una ganancia baja), pero a medida que aumenta la ganancia, rápidamente se hace necesaria una capacitancia de compensación (es decir, en la figura 4, el condensador de compensación C _C aumenta rápidamente con la ganancia) porque la relación polar necesaria aumenta con la ganancia. Para una ganancia aún mayor, el C _C necesario disminuye con el aumento de la ganancia porque la amplificación de Miller de C _C , que aumenta con la ganancia (consulte la ecuación de Miller ), permite un valor más pequeño para C _C .

Para proporcionar un mayor margen de seguridad para las incertidumbres de diseño, a menudo A _v se incrementa a dos o tres veces A _v en el lado derecho de esta ecuación. ^[14] Consulte Sansen ^[4] o Huijsing ^[10] y el artículo sobre respuesta al escalón .

Velocidad de giro

Lo anterior es un análisis de señal pequeña. Sin embargo, cuando se utilizan señales grandes, la necesidad de cargar y descargar el condensador de compensación afecta negativamente la velocidad de respuesta del amplificador ; en particular, la respuesta a una señal de rampa de entrada está limitada por la necesidad de cargar C _C .

Véase también

• Compensación de frecuencia
• Efecto Miller
• Fuente común
• Diagrama de Bode
• Respuesta escalonada
• Amplificador CMOS

Referencias y notas

1. Es decir, el tiempo de subida se selecciona para que sea lo más rápido posible, consistente con un bajo sobreimpulso y timbre .
2. C. Toumazu, Moschytz GS y Gilbert B (Editores) (2007). Compensaciones en el diseño de circuitos analógicos: el compañero del diseñador. Nueva York/Berlín/Dordrecht: Springer. pp. 272–275. ISBN 978-1-4020-7037-2. {{cite book}}: |author=tiene nombre genérico ( ayuda )
3. Marc T. Thompson (2006). Diseño intuitivo de circuitos analógicos: un enfoque de resolución de problemas utilizando estudios de casos de diseño. Ámsterdam: Elsevier Newnes. p. 200. ISBN 0-7506-7786-4.
4. Willy MC Sansen (2006). Conceptos básicos del diseño analógico. Nueva York; Berlín: Springer. págs. §097, pág. 266 y siguientes . ISBN 0-387-25746-2.
5. Aunque este ejemplo parece muy específico, el análisis matemático asociado se utiliza mucho en el diseño de circuitos.
6. La suma de las constantes de tiempo es el coeficiente del término lineal en jω y el producto de las constantes de tiempo es el coeficiente del término cuadrático en (jω) ² .
7. La expresión para difiere un poco de ( C _M +C _i ) ( R _A || R _i ) como se encontró inicialmente para f ₁ , pero la diferencia es menor asumiendo que la capacitancia de carga no es tan grande como para controlar la respuesta de baja frecuencia en lugar de la capacitancia de Miller. ${\displaystyle \tau _{1}}$
8. Por cierto, cuanto más alta sea la frecuencia del polo de alta frecuencia, más probable será que en un amplificador real intervengan otros polos (no considerados en este análisis).
9. AS Sedra y KC Smith (2004). Circuitos microelectrónicos (quinta edición). Nueva York: Oxford University Press. pp. 849 y Example 8.6, p. 853. ISBN 0-19-514251-9.
10. Huijsing, Johan H. (2001). Amplificadores operacionales: teoría y diseño. Boston, MA: Kluwer Academic. pp. §6.2, pp.205–206 y Figura 6.2.1. ISBN 0-7923-7284-0.
11. Feucht, Dennis: compensación bipolar
12. Self, Douglas (2006). Manual de diseño de amplificadores de potencia de audio. Oxford: Newnes. pp. 191–193. ISBN 0-7506-8072-5.
13. Es decir, la frecuencia se representa gráficamente en potencias de diez, como 1, 10, 10 ² , etc.
14. Un factor de dos da como resultado el diseño de máxima superficie o Butterworth para un amplificador de dos polos. Sin embargo, los amplificadores reales tienen más de dos polos y, a menudo, es necesario un factor mayor que dos.

Enlaces externos

• Diagramas de Bode en el Wikilibro de Teoría de Circuitos
• Diagramas de Bode en el Wikilibro de Sistemas de Control