Dislocación parcial

Forma descompuesta de dislocación que ocurre dentro de un material cristalino.

En la ciencia de los materiales , una dislocación parcial es una forma descompuesta de dislocación que se produce dentro de un material cristalino . Una dislocación extendida es una dislocación que se ha disociado en un par de dislocaciones parciales. La suma vectorial de los vectores de Burgers de las dislocaciones parciales es el vector de Burgers de la dislocación extendida.

Favorabilidad de la reacción

Una dislocación se descompondrá en dislocaciones parciales si el estado energético de la suma de las dislocaciones parciales es menor que el estado energético de la dislocación original. Esto se resume en el criterio energético de Frank :

${\displaystyle {\begin{aligned}|{\boldsymbol {b_{1}}}|^{2}>&|{\boldsymbol {b_{2}}}|^{2}+|{\boldsymbol {b_{3}}}|^{2}{\text{ (favorable, will decompose)}}\\|{\boldsymbol {b_{1}}}|^{2}<&|{\boldsymbol {b_{2}}}|^{2}+|{\boldsymbol {b_{3}}}|^{2}{\text{ (not favorable, will not decompose)}}\\|{\boldsymbol {b_{1}}}|^{2}=&|{\boldsymbol {b_{2}}}|^{2}+|{\boldsymbol {b_{3}}}|^{2}{\text{ (will remain in original state)}}\end{aligned}}}$

Luxaciones parciales de Shockley

Las dislocaciones parciales de Shockley generalmente se refieren a un par de dislocaciones que pueden provocar la presencia de fallas de apilamiento . Este par de dislocaciones parciales puede permitir el movimiento de dislocaciones al permitir una ruta alternativa para el movimiento atómico.

${\displaystyle {\begin{aligned}{\boldsymbol {b_{1}}}\rightarrow {\boldsymbol {b_{2}}}+{\boldsymbol {b_{3}}}\end{aligned}}}$

En los sistemas FCC, un ejemplo de descomposición de Shockley es:

${\displaystyle {\begin{aligned}{\frac {a}{2}}[10{\overline {1}}]\rightarrow {\frac {a}{6}}[2{\overline {1}}{\overline {1}}]+{\frac {a}{6}}[11{\overline {2}}]\end{aligned}}}$

¿Qué es energéticamente favorable?

${\displaystyle {\begin{aligned}|{\frac {a}{2}}{\sqrt {1^{2}+0^{2}+(-1)^{2}}}|^{2}>&|{\frac {a}{6}}{\sqrt {2^{2}+(-1)^{2}+(-1)^{2}}}|^{2}+|{\frac {a}{6}}{\sqrt {1^{2}+1^{2}+(-2)^{2}}}|^{2}\\{\frac {a^{2}}{2}}>&{\frac {a^{2}}{6}}+{\frac {a^{2}}{6}}\end{aligned}}}$

Los componentes de los parciales de Shockley deben sumarse al vector original que se está descomponiendo:

${\displaystyle {\begin{aligned}{\frac {a}{2}}(1)=&{\frac {a}{6}}(2)+{\frac {a}{6}}(1)\\{\frac {a}{2}}(0)=&{\frac {a}{6}}(-1)+{\frac {a}{6}}(1)\\{\frac {a}{2}}(-1)=&{\frac {a}{6}}(-1)+{\frac {a}{6}}(-2)\end{aligned}}}$

Dislocaciones parciales francas

Las dislocaciones parciales de Frank son sésiles (inmóviles), pero pueden moverse por difusión de átomos. ^[1] En los sistemas FCC, las dislocaciones parciales de Frank se dan por:

${\displaystyle {\begin{aligned}{\boldsymbol {b}}_{\text{frank}}=&{\frac {a}{3}}[{\text{1 1 1}}]\end{aligned}}}$

Tetraedro de Thompson

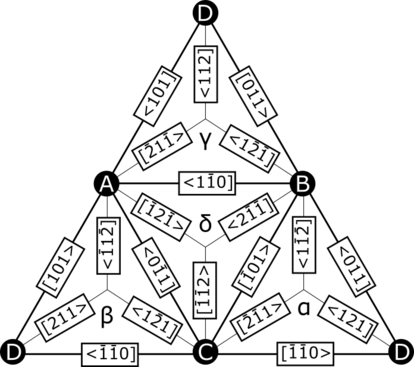
Para los cristales FCC, los tetraedros de Thompson o la notación de Thompson son una notación inventada para describir más fácilmente las dislocaciones parciales. En una celda unitaria dada, marque el punto A en el origen, el punto B en a/2 [110], el punto C en a/2 [011] y el punto D en a/2 [101]; estos puntos forman los vértices de un tetraedro. Luego, marque el centro de las caras opuestas para cada punto como α, β, γ y δ, respectivamente. ^[2] Con esto, la representación geométrica de un tetraedro de Thompson está completa.

Tetraedro de Thompson dibujado dentro de un cristal FCC y luego rotado para ver más fácilmente las caras y los vértices.

Cualquier combinación de letras romanas describe un miembro de los planos de deslizamiento {111} en un cristal FCC. Un vector formado por dos letras romanas describe el vector de Burgers de una dislocación perfecta. Si el vector está formado por una letra romana y una griega, entonces es un parcial de Frank si las letras son correspondientes (Aα, Bβ,...) o un parcial de Shockley en caso contrario (Aβ, Aγ,...). Los vectores formados por dos letras griegas describen dislocaciones en escalera. Utilizando la notación de Thompson, se pueden añadir vectores de Burgers para describir otras dislocaciones y mecanismos. Por ejemplo, se pueden añadir dos dislocaciones parciales de Shockley para formar una dislocación perfecta: Aβ + βC = AC. ^[2] Es necesario que las letras interiores de una operación dada coincidan, pero se pueden añadir muchas en secuencia para describir mecanismos más complejos.

Es útil resumir esta información utilizando un tetraedro de Thompson desplegado.

Los tetraedros de Thompson desplegados contienen información para ver rápidamente las direcciones relativas de los vectores de Burgers en una estructura FCC.

Esclusa Lomer-Cottrell

La dislocación de Lomer-Cottrell se forma a través de una reacción de dislocación más compleja. Por ejemplo, considere dos dislocaciones extendidas: DB = Dγ + γB y BC = Bδ + δC. Cuando se encuentran, es más favorable energéticamente formar una única dislocación, DC = DB + BC = Dγ + γB + Bδ + δC = Dγ + γδ + δC. Las dislocaciones parciales posteriores de cada dislocación extendida forman ahora una dislocación parcial en forma de escalera. Esta estructura conduce a una movilidad reducida de las dislocaciones, ya que la estructura del núcleo no es plana (lo que significa que no cruza a lo largo de la cara del tetraedro). ^[2] Esta reducción de la movilidad transforma la dislocación de Lomer-Cottrell en un obstáculo para otras dislocaciones, fortaleciendo así el material.

Implicaciones mecánicas

Al formarse fallas de apilamiento, las dislocaciones parciales alcanzan un equilibrio cuando la energía repulsiva entre dislocaciones parciales coincide con la energía atractiva de la falla de apilamiento. Esto significa que los materiales con mayor energía de falla de apilamiento, es decir, aquellos con alto módulo de corte y grandes vectores de Burgers, tendrán una distancia menor entre dislocaciones parciales. Por el contrario, los materiales con baja energía de falla de apilamiento tendrán grandes distancias entre dislocaciones parciales. ^[3]

Las dislocaciones parciales se mueven libremente, pero para poder deslizarse hacia un plano diferente, primero deben contraerse antes de deslizarse hacia un plano diferente.

Para que se produzca un deslizamiento cruzado , ambas dislocaciones parciales deben cambiar de plano de deslizamiento. El mecanismo común de Friedel-Escaig requiere que las dislocaciones parciales se recombinen en un punto antes de producirse un deslizamiento cruzado sobre un plano de deslizamiento diferente. ^[2] Para juntar las dislocaciones parciales es necesario aplicar suficiente esfuerzo cortante para reducir la distancia entre ellas, por lo que las dislocaciones parciales con bajas energías de falla de apilamiento serán inherentemente más difíciles de juntar y, por lo tanto, más difíciles de producir un deslizamiento cruzado. ^{[3] [4]} Por el contrario, los materiales con alta energía de falla de apilamiento serán más fáciles de producir un deslizamiento cruzado.

Cuanto más fácilmente pueda deslizarse transversalmente una dislocación, más libremente podrá moverse alrededor de obstáculos, lo que dificulta el endurecimiento por deformación. Por lo tanto, los materiales que permiten un fácil deslizamiento transversal (alta energía de falla de apilamiento) experimentarán menos endurecimiento por deformación y fortalecimiento con métodos como el fortalecimiento por solución sólida.

Referencias

1. Meyers y Chawla. (1999) Comportamientos mecánicos de los materiales. Prentice Hall, Inc. 217.
2. Cai, Wei; Nix, William (2016), Imperfecciones en sólidos cristalinos , págs. 349–375
3. Courtney, Thomas, Comportamiento mecánico de los materiales, segunda edición , págs. 117-119
4. Hull, D.; Bacon, DJ (2011), Introducción a las dislocaciones (quinta edición)