Determinante

En matemáticas, invariante de matrices cuadradas.

En matemáticas , el determinante es una función escalar de los elementos de una matriz cuadrada . El determinante de una matriz A se denota comúnmente como det( A ) , det A o | A | . Su valor caracteriza algunas propiedades de la matriz y la función lineal representada, sobre una base dada , por la matriz. En particular, el determinante es distinto de cero si y solo si la matriz es invertible y la función lineal correspondiente es un isomorfismo .

El determinante está completamente determinado por las dos propiedades siguientes: el determinante de un producto de matrices es el producto de sus determinantes, y el determinante de una matriz triangular es el producto de sus entradas diagonales.

El determinante de una matriz 2 × 2 es

${\displaystyle {\begin{vmatrix}a&b\\c&d\end{vmatrix}}=ad-bc,}$

y el determinante de una matriz de 3 × 3 es

${\displaystyle {\begin{vmatrix}a&b&c\\d&e&f\\g&h&i\end{vmatrix}}=aei+bfg+cdh-ceg-bdi-afh.}$

El determinante de una matriz n × n se puede definir de varias formas equivalentes, siendo la más común la fórmula de Leibniz , que expresa el determinante como una suma de (el factorial de n ) productos con signo de las entradas de la matriz. Se puede calcular mediante la expansión de Laplace , que expresa el determinante como una combinación lineal de determinantes de submatrices, o con eliminación gaussiana , que permite calcular una forma escalonada por filas con el mismo determinante, igual al producto de las entradas diagonales de la forma escalonada por filas. ${\displaystyle n!}$

Los determinantes también se pueden definir por algunas de sus propiedades. En concreto, el determinante es la única función definida en las matrices n × n que tiene las cuatro propiedades siguientes:

1. El determinante de la matriz identidad es 1 .
2. El intercambio de dos filas multiplica el determinante por −1 .
3. Al multiplicar una fila por un número se multiplica el determinante por este número.
4. Sumar un múltiplo de una fila a otra fila no cambia el determinante.

Las propiedades anteriores relacionadas con las filas (propiedades 2 a 4) pueden reemplazarse por las declaraciones correspondientes con respecto a las columnas.

El determinante es invariante bajo semejanza matricial . Esto implica que, dado un endomorfismo lineal de un espacio vectorial de dimensión finita , el determinante de la matriz que lo representa sobre una base no depende de la base elegida. Esto permite definir el determinante de un endomorfismo lineal, que no depende de la elección de un sistema de coordenadas .

Los determinantes aparecen en todas las matemáticas. Por ejemplo, una matriz se utiliza a menudo para representar los coeficientes en un sistema de ecuaciones lineales , y los determinantes se pueden utilizar para resolver estas ecuaciones ( regla de Cramer ), aunque otros métodos de solución son computacionalmente mucho más eficientes. Los determinantes se utilizan para definir el polinomio característico de una matriz cuadrada, cuyas raíces son los valores propios . En geometría , el volumen n -dimensional con signo de un paralelepípedo n -dimensional se expresa mediante un determinante, y el determinante de un endomorfismo lineal determina cómo se transforman la orientación y el volumen n -dimensional bajo el endomorfismo. Esto se utiliza en cálculo con formas diferenciales externas y el determinante jacobiano , en particular para cambios de variables en integrales múltiples .

Matrices de dos por dos

El determinante de una matriz 2 × 2 se denota mediante " det " o mediante barras verticales alrededor de la matriz y se define como ${\displaystyle {\begin{pmatrix}a&b\\c&d\end{pmatrix}}}$

${\displaystyle \det {\begin{pmatrix}a&b\\c&d\end{pmatrix}}={\begin{vmatrix}a&b\\c&d\end{vmatrix}}=ad-bc.}$

Por ejemplo,

${\displaystyle \det {\begin{pmatrix}3&7\\1&-4\end{pmatrix}}={\begin{vmatrix}3&7\\1&{-4}\end{vmatrix}}=(3\cdot (-4))-(7\cdot 1)=-19.}$

Primeras propiedades

El determinante tiene varias propiedades clave que pueden demostrarse mediante la evaluación directa de la definición de matrices y que siguen siendo válidas para determinantes de matrices mayores. Son las siguientes: ^[1] en primer lugar, el determinante de la matriz identidad es 1. En segundo lugar, el determinante es cero si dos filas son iguales: ${\displaystyle 2\times 2}$ ${\displaystyle {\begin{pmatrix}1&0\\0&1\end{pmatrix}}}$

${\displaystyle {\begin{vmatrix}a&b\\a&b\end{vmatrix}}=ab-ba=0.}$

Esto se aplica de manera similar si las dos columnas son iguales. Además,

${\displaystyle {\begin{vmatrix}a&b+b'\\c&d+d'\end{vmatrix}}=a(d+d')-(b+b')c={\begin{vmatrix}a&b\\c&d\end{vmatrix}}+{\begin{vmatrix}a&b'\\c&d'\end{vmatrix}}.}$

Finalmente, si alguna columna se multiplica por algún número (es decir, todas las entradas en esa columna se multiplican por ese número), el determinante también se multiplica por ese número: ${\displaystyle r}$

${\displaystyle {\begin{vmatrix}r\cdot a&b\\r\cdot c&d\end{vmatrix}}=rad-brc=r(ad-bc)=r\cdot {\begin{vmatrix}a&b\\c&d\end{vmatrix}}.}$

Significado geométrico

El área del paralelogramo es el valor absoluto del determinante de la matriz formada por los vectores que representan los lados del paralelogramo.

Si las entradas de la matriz son números reales, la matriz A puede utilizarse para representar dos aplicaciones lineales : una que asigna los vectores base estándar a las filas de A y otra que los asigna a las columnas de A. En cualquier caso, las imágenes de los vectores base forman un paralelogramo que representa la imagen del cuadrado unitario bajo la aplicación. El paralelogramo definido por las filas de la matriz anterior es el que tiene vértices en (0, 0) , ( a , b ) , ( a + c , b + d ) y ( c , d ) , como se muestra en el diagrama adjunto.

El valor absoluto de ad − bc es el área del paralelogramo y, por lo tanto, representa el factor de escala por el cual las áreas son transformadas por A . (El paralelogramo formado por las columnas de A es en general un paralelogramo diferente, pero como el determinante es simétrico con respecto a filas y columnas, el área será la misma).

El valor absoluto del determinante junto con el signo se convierte en el área con signo del paralelogramo. El área con signo es la misma que el área habitual , excepto que es negativa cuando el ángulo entre el primer y el segundo vector que define el paralelogramo gira en el sentido de las agujas del reloj (que es opuesto a la dirección que se obtendría para la matriz identidad ).

Para demostrar que ad − bc es el área con signo, se puede considerar una matriz que contiene dos vectores u ≡ ( a , b ) y v ≡ ( c , d ) que representan los lados del paralelogramo. El área con signo se puede expresar como | u | | v | sen θ para el ángulo θ entre los vectores, que es simplemente la base por la altura, la longitud de un vector por el componente perpendicular del otro. Debido al seno , esta ya es el área con signo, pero se puede expresar de manera más conveniente utilizando el coseno del ángulo complementario a un vector perpendicular, por ejemplo, u ^⊥ = (− b , a ) , de modo que | u ^⊥ | | v | cos θ′ se convierte en el área con signo en cuestión, que se puede determinar por el patrón del producto escalar como igual a ad − bc de acuerdo con las siguientes ecuaciones:

${\displaystyle {\text{Signed area}}=|{\boldsymbol {u}}|\,|{\boldsymbol {v}}|\,\sin \,\theta =\left|{\boldsymbol {u}}^{\perp }\right|\,\left|{\boldsymbol {v}}\right|\,\cos \,\theta '={\begin{pmatrix}-b\\a\end{pmatrix}}\cdot {\begin{pmatrix}c\\d\end{pmatrix}}=ad-bc.}$

El volumen de este paralelepípedo es el valor absoluto del determinante de la matriz formada por las columnas construidas a partir de los vectores r1, r2 y r3.

Por lo tanto, el determinante proporciona el factor de escala y la orientación inducida por la aplicación representada por A. Cuando el determinante es igual a uno, la aplicación lineal definida por la matriz es equiárea y preserva la orientación.

El objeto conocido como bivector está relacionado con estas ideas. En 2D, se puede interpretar como un segmento plano orientado formado al imaginar dos vectores, cada uno con origen (0, 0) y coordenadas ( a , b ) y ( c , d ) . La magnitud del bivector (denotada por ( a , b ) ∧ ( c , d ) ) es el área con signo , que también es el determinante ad − bc . ^[2]

Si una matriz real A de n × n se escribe en términos de sus vectores columna , entonces ${\displaystyle A=\left[{\begin{array}{c|c|c|c}\mathbf {a} _{1}&\mathbf {a} _{2}&\cdots &\mathbf {a} _{n}\end{array}}\right]}$

${\displaystyle A{\begin{pmatrix}1\\0\\\vdots \\0\end{pmatrix}}=\mathbf {a} _{1},\quad A{\begin{pmatrix}0\\1\\\vdots \\0\end{pmatrix}}=\mathbf {a} _{2},\quad \ldots ,\quad A{\begin{pmatrix}0\\0\\\vdots \\1\end{pmatrix}}=\mathbf {a} _{n}.}$

Esto significa que asigna el cubo unitario n al paralelotopo n -dimensional definido por los vectores de la región ${\displaystyle A}$ ${\displaystyle \mathbf {a} _{1},\mathbf {a} _{2},\ldots ,\mathbf {a} _{n},}$ ${\displaystyle P=\left\{c_{1}\mathbf {a} _{1}+\cdots +c_{n}\mathbf {a} _{n}\mid 0\leq c_{i}\leq 1\ \forall i\right\}.}$

El determinante da el volumen n -dimensional con signo de este paraleletopo, y por lo tanto describe de manera más general el factor de escala del volumen n -dimensional de la transformación lineal producida por A . ^[3] (El signo muestra si la transformación conserva o invierte la orientación .) En particular, si el determinante es cero, entonces este paraleletopo tiene volumen cero y no es completamente n -dimensional, lo que indica que la dimensión de la imagen de A es menor que n . Esto significa que A produce una transformación lineal que no es ni sobre ni biunívoca , y por lo tanto no es invertible. ${\displaystyle \det(A)=\pm {\text{vol}}(P),}$

Definición

Sea A una matriz cuadrada con n filas y n columnas, de modo que pueda escribirse como

${\displaystyle A={\begin{bmatrix}a_{1,1}&a_{1,2}&\cdots &a_{1,n}\\a_{2,1}&a_{2,2}&\cdots &a_{2,n}\\\vdots &\vdots &\ddots &\vdots \\a_{n,1}&a_{n,2}&\cdots &a_{n,n}\end{bmatrix}}.}$

Las entradas, etc., son, para muchos propósitos, números reales o complejos. Como se analiza a continuación, el determinante también se define para matrices cuyas entradas están en un anillo conmutativo . ${\displaystyle a_{1,1}}$

El determinante de A se denota por det( A ), o puede denotarse directamente en términos de las entradas de la matriz escribiendo barras envolventes en lugar de corchetes:

${\displaystyle {\begin{vmatrix}a_{1,1}&a_{1,2}&\cdots &a_{1,n}\\a_{2,1}&a_{2,2}&\cdots &a_{2,n}\\\vdots &\vdots &\ddots &\vdots \\a_{n,1}&a_{n,2}&\cdots &a_{n,n}\end{vmatrix}}.}$

Existen varias formas equivalentes de definir el determinante de una matriz cuadrada A , es decir, una con el mismo número de filas y columnas: el determinante se puede definir mediante la fórmula de Leibniz , una fórmula explícita que implica sumas de productos de ciertas entradas de la matriz. El determinante también se puede caracterizar como la función única que depende de las entradas de la matriz que satisfacen ciertas propiedades. Este enfoque también se puede utilizar para calcular determinantes simplificando las matrices en cuestión.

Fórmula de Leibniz

Matrices de 3 × 3

La fórmula de Leibniz para el determinante de una matriz de 3 × 3 es la siguiente:

${\displaystyle {\begin{vmatrix}a&b&c\\d&e&f\\g&h&i\end{vmatrix}}=aei+bfg+cdh-ceg-bdi-afh.\ }$

En esta expresión, cada término tiene un factor de cada fila, todos en diferentes columnas, dispuestos en orden creciente de fila. Por ejemplo, bdi tiene b de la primera fila segunda columna, d de la segunda fila primera columna, e i de la tercera fila tercera columna. Los signos están determinados por cuántas transposiciones de factores son necesarias para organizar los factores en orden creciente de sus columnas (dado que los términos están ordenados de izquierda a derecha en orden creciente de fila): positivo para un número par de transposiciones y negativo para un número impar. Para el ejemplo de bdi , la transposición simple de bd a db da dbi, cuyos tres factores son de la primera, segunda y tercera columnas respectivamente; este es un número impar de transposiciones, por lo que el término aparece con signo negativo.

Regla de Sarrus

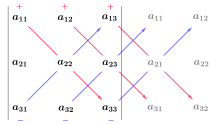
La regla de Sarrus es una regla mnemotécnica para la forma expandida de este determinante: la suma de los productos de tres líneas diagonales de elementos de la matriz en dirección noroeste a sureste, menos la suma de los productos de tres líneas diagonales de elementos en dirección suroeste a noreste, cuando las copias de las dos primeras columnas de la matriz se escriben al lado, como en la ilustración. Este esquema para calcular el determinante de una matriz de 3 × 3 no se traslada a dimensiones superiores.

norte×nortematrices

Generalizando lo anterior a dimensiones superiores, el determinante de una matriz es una expresión que involucra permutaciones y sus signaturas . Una permutación del conjunto es una función biyectiva de este conjunto a sí mismo, con valores que agotan todo el conjunto. El conjunto de todas esas permutaciones, llamado grupo simétrico , se denota comúnmente como . La signatura de una permutación es si la permutación se puede obtener con un número par de transposiciones (intercambios de dos entradas); de lo contrario, es ${\displaystyle n\times n}$ ${\displaystyle \{1,2,\dots ,n\}}$ ${\displaystyle \sigma }$ ${\displaystyle \sigma (1),\sigma (2),\ldots ,\sigma (n)}$ ${\displaystyle S_{n}}$ ${\displaystyle \operatorname {sgn}(\sigma )}$ ${\displaystyle \sigma }$ ${\displaystyle +1,}$ ${\displaystyle -1.}$

Dada una matriz

${\displaystyle A={\begin{bmatrix}a_{1,1}\ldots a_{1,n}\\\vdots \qquad \vdots \\a_{n,1}\ldots a_{n,n}\end{bmatrix}},}$

La fórmula de Leibniz para su determinante es, utilizando la notación sigma para la suma,

${\displaystyle \det(A)={\begin{vmatrix}a_{1,1}\ldots a_{1,n}\\\vdots \qquad \vdots \\a_{n,1}\ldots a_{n,n}\end{vmatrix}}=\sum _{\sigma \in S_{n}}\operatorname {sgn}(\sigma )a_{1,\sigma (1)}\cdots a_{n,\sigma (n)}.}$

Usando la notación pi para el producto, esto se puede abreviar en

${\displaystyle \det(A)=\sum _{\sigma \in S_{n}}\left(\operatorname {sgn}(\sigma )\prod _{i=1}^{n}a_{i,\sigma (i)}\right)}$.

El símbolo de Levi-Civita se define en las n - tuplas de números enteros como 0 si dos de los números enteros son iguales, y en caso contrario como la firma de la permutación definida por la n -tupla de números enteros. Con el símbolo de Levi-Civita, la fórmula de Leibniz se convierte en ${\displaystyle \varepsilon _{i_{1},\ldots ,i_{n}}}$ ${\displaystyle \{1,\ldots ,n\}}$

${\displaystyle \det(A)=\sum _{i_{1},i_{2},\ldots ,i_{n}}\varepsilon _{i_{1}\cdots i_{n}}a_{1,i_{1}}\!\cdots a_{n,i_{n}},}$

donde la suma se toma sobre todas las n -tuplas de números enteros en ^{[4] [5]} ${\displaystyle \{1,\ldots ,n\}.}$

Propiedades

Caracterización del determinante

El determinante se puede caracterizar por las tres propiedades clave siguientes. Para expresarlas, es conveniente considerar que una matriz A está compuesta por sus columnas, denotadas así: ${\displaystyle n\times n}$ ${\displaystyle n}$

${\displaystyle A={\big (}a_{1},\dots ,a_{n}{\big )},}$

donde el vector columna (para cada i ) está compuesto por las entradas de la matriz en la i -ésima columna. ${\displaystyle a_{i}}$

2. ${\displaystyle \det \left(I\right)=1}$, donde es una matriz identidad . ${\displaystyle I}$
4. El determinante es multilineal : si la j -ésima columna de una matriz se escribe como una combinación lineal de dos vectores columna v y w y un número r , entonces el determinante de A se puede expresar como una combinación lineal similar: ${\displaystyle A}$ ${\displaystyle a_{j}=r\cdot v+w}$

   ${\displaystyle {\begin{aligned}|A|&={\big |}a_{1},\dots ,a_{j-1},r\cdot v+w,a_{j+1},\dots ,a_{n}|\\&=r\cdot |a_{1},\dots ,v,\dots a_{n}|+|a_{1},\dots ,w,\dots ,a_{n}|\end{aligned}}}$

6. El determinante es alterno : siempre que dos columnas de una matriz sean idénticas, su determinante es 0:

   ${\displaystyle |a_{1},\dots ,v,\dots ,v,\dots ,a_{n}|=0.}$

Si el determinante se define utilizando la fórmula de Leibniz como se ha indicado anteriormente, estas tres propiedades se pueden demostrar mediante la inspección directa de dicha fórmula. Algunos autores también abordan el determinante directamente utilizando estas tres propiedades: se puede demostrar que existe exactamente una función que asigna a cualquier matriz A un número que satisface estas tres propiedades. ^[6] Esto también demuestra que este enfoque más abstracto del determinante produce la misma definición que el que utiliza la fórmula de Leibniz. ${\displaystyle n\times n}$

Para comprobarlo basta con expandir el determinante por multilinealidad en las columnas hasta obtener una (enorme) combinación lineal de determinantes de matrices en la que cada columna es un vector base estándar . Estos determinantes son o bien 0 (por la propiedad 9) o bien ±1 (por las propiedades 1 y 12 que aparecen a continuación), de modo que la combinación lineal da la expresión anterior en términos del símbolo de Levi-Civita. Aunque tiene un aspecto menos técnico, esta caracterización no puede sustituir por completo a la fórmula de Leibniz para definir el determinante, ya que sin ella no está clara la existencia de una función apropiada. ^{[ cita requerida ]}

Consecuencias inmediatas

Estas reglas tienen varias consecuencias adicionales:

• El determinante es una función homogénea , es decir, (para una matriz ). $${\displaystyle \det(cA)=c^{n}\det(A)}$$ ${\displaystyle n\times n}$ ${\displaystyle A}$
• Al intercambiar cualquier par de columnas de una matriz, se multiplica su determinante por −1. Esto se deduce de que el determinante es multilineal y alterno (propiedades 2 y 3 anteriores): Esta fórmula se puede aplicar de forma iterativa cuando se intercambian varias columnas. Por ejemplo , de forma más general, cualquier permutación de las columnas multiplica el determinante por el signo de la permutación. $${\displaystyle |a_{1},\dots ,a_{j},\dots a_{i},\dots ,a_{n}|=-|a_{1},\dots ,a_{i},\dots ,a_{j},\dots ,a_{n}|.}$$ $${\displaystyle |a_{3},a_{1},a_{2},a_{4}\dots ,a_{n}|=-|a_{1},a_{3},a_{2},a_{4},\dots ,a_{n}|=|a_{1},a_{2},a_{3},a_{4},\dots ,a_{n}|.}$$
• Si alguna columna puede expresarse como una combinación lineal de las otras columnas (es decir, las columnas de la matriz forman un conjunto linealmente dependiente ), el determinante es 0. Como caso especial, esto incluye: si alguna columna es tal que todas sus entradas son cero, entonces el determinante de esa matriz es 0.
• La suma de un múltiplo escalar de una columna a otra columna no cambia el valor del determinante. Esto es una consecuencia de la multilinealidad y de ser alterna: por multilinealidad el determinante cambia por un múltiplo del determinante de una matriz con dos columnas iguales, cuyo determinante es 0, ya que el determinante es alternado.
• Si es una matriz triangular , es decir , siempre que o, alternativamente, siempre que , entonces su determinante es igual al producto de las entradas diagonales: De hecho, una matriz de este tipo se puede reducir, añadiendo apropiadamente múltiplos de las columnas con menos entradas distintas de cero a aquellas con más entradas, a una matriz diagonal (sin cambiar el determinante). Para una matriz de este tipo, el uso de la linealidad en cada columna reduce a la matriz identidad, en cuyo caso la fórmula establecida se cumple por la primera propiedad caracterizadora de los determinantes. Alternativamente, esta fórmula también se puede deducir de la fórmula de Leibniz, ya que la única permutación que da una contribución distinta de cero es la permutación identidad. ${\displaystyle A}$ ${\displaystyle a_{ij}=0}$ ${\displaystyle i>j}$ ${\displaystyle i<j}$ $${\displaystyle \det(A)=a_{11}a_{22}\cdots a_{nn}=\prod _{i=1}^{n}a_{ii}.}$$ ${\displaystyle \sigma }$

Ejemplo

Estas propiedades características y sus consecuencias enumeradas anteriormente son teóricamente significativas, pero también se pueden utilizar para calcular determinantes de matrices concretas. De hecho, la eliminación gaussiana se puede aplicar para convertir cualquier matriz en forma triangular superior, y los pasos de este algoritmo afectan al determinante de una manera controlada. El siguiente ejemplo concreto ilustra el cálculo del determinante de la matriz utilizando ese método: ${\displaystyle A}$

${\displaystyle A={\begin{bmatrix}-2&-1&2\\2&1&4\\-3&3&-1\end{bmatrix}}.}$

Combinando estas igualdades obtenemos ${\displaystyle |A|=-|E|=-(18\cdot 3\cdot (-1))=54.}$

Transponer

El determinante de la transpuesta de es igual al determinante de A : ${\displaystyle A}$

${\displaystyle \det \left(A^{\textsf {T}}\right)=\det(A)}$.

Esto se puede demostrar examinando la fórmula de Leibniz. ^[7] Esto implica que en todas las propiedades mencionadas anteriormente, la palabra "columna" se puede reemplazar por "fila" en todas partes. Por ejemplo, si consideramos una matriz n × n como compuesta de n filas, el determinante es una función n -lineal.

Multiplicatividad y grupos matriciales

El determinante es una función multiplicativa , es decir, para matrices cuadradas y de igual tamaño, el determinante de un producto matricial es igual al producto de sus determinantes: ${\displaystyle A}$ ${\displaystyle B}$

${\displaystyle \det(AB)=\det(A)\det(B)}$

Este hecho clave se puede demostrar observando que, para una matriz fija , ambos lados de la ecuación son alternados y multilineales en función de las columnas de . Además, ambos toman el valor cuando es la matriz identidad. La caracterización única mencionada anteriormente de los mapas multilineales alternados demuestra, por lo tanto, esta afirmación. ^[8] ${\displaystyle B}$ ${\displaystyle A}$ ${\displaystyle \det B}$ ${\displaystyle A}$

Una matriz con entradas en un campo es invertible precisamente si su determinante es distinto de cero. Esto se deduce de la multiplicidad del determinante y de la fórmula para la inversa que involucra a la matriz adjunta mencionada a continuación. En este caso, el determinante de la matriz inversa está dado por ${\displaystyle A}$

${\displaystyle \det \left(A^{-1}\right)={\frac {1}{\det(A)}}=[\det(A)]^{-1}}$.

En particular, los productos e inversos de matrices con determinante distinto de cero (respectivamente, determinante uno) aún tienen esta propiedad. Por lo tanto, el conjunto de tales matrices (de tamaño fijo sobre un cuerpo ) forma un grupo conocido como el grupo lineal general (respectivamente, un subgrupo llamado el grupo lineal especial . De manera más general, la palabra "especial" indica el subgrupo de otro grupo matricial de matrices de determinante uno. Los ejemplos incluyen el grupo ortogonal especial (que si n es 2 o 3 consiste en todas las matrices de rotación ), y el grupo unitario especial . ${\displaystyle n}$ ${\displaystyle K}$ ${\displaystyle \operatorname {GL} _{n}(K)}$ ${\displaystyle \operatorname {SL} _{n}(K)\subset \operatorname {GL} _{n}(K)}$

Como el determinante respeta la multiplicación y las inversas, es de hecho un homomorfismo de grupo de en el grupo multiplicativo de elementos distintos de cero de . Este homomorfismo es sobreyectivo y su núcleo es (las matrices con determinante uno). Por lo tanto, por el primer teorema de isomorfismo , esto demuestra que es un subgrupo normal de , y que el grupo cociente es isomorfo a . ${\displaystyle \operatorname {GL} _{n}(K)}$ ${\displaystyle K^{\times }}$ ${\displaystyle K}$ ${\displaystyle \operatorname {SL} _{n}(K)}$ ${\displaystyle \operatorname {SL} _{n}(K)}$ ${\displaystyle \operatorname {GL} _{n}(K)}$ ${\displaystyle \operatorname {GL} _{n}(K)/\operatorname {SL} _{n}(K)}$ ${\displaystyle K^{\times }}$

La fórmula de Cauchy-Binet es una generalización de esa fórmula del producto para matrices rectangulares . Esta fórmula también puede reformularse como una fórmula multiplicativa para matrices compuestas cuyos elementos son los determinantes de todas las submatrices cuadráticas de una matriz dada. ^{[9] [10]}

Expansión de Laplace

La expansión de Laplace expresa el determinante de una matriz recursivamente en términos de determinantes de matrices más pequeñas, conocidas como sus menores . El menor se define como el determinante de la matriz que resulta de eliminar la fila -ésima y la columna -ésima. La expresión se conoce como cofactor . Para cada , se tiene la igualdad ${\displaystyle A}$ ${\displaystyle M_{i,j}}$ ${\displaystyle (n-1)\times (n-1)}$ ${\displaystyle A}$ ${\displaystyle i}$ ${\displaystyle j}$ ${\displaystyle (-1)^{i+j}M_{i,j}}$ ${\displaystyle i}$

${\displaystyle \det(A)=\sum _{j=1}^{n}(-1)^{i+j}a_{i,j}M_{i,j},}$

que se denomina expansión de Laplace a lo largo de la fila i . Por ejemplo, la expansión de Laplace a lo largo de la primera fila ( ) da la siguiente fórmula: ${\displaystyle i=1}$

${\displaystyle {\begin{vmatrix}a&b&c\\d&e&f\\g&h&i\end{vmatrix}}=a{\begin{vmatrix}e&f\\h&i\end{vmatrix}}-b{\begin{vmatrix}d&f\\g&i\end{vmatrix}}+c{\begin{vmatrix}d&e\\g&h\end{vmatrix}}}$

Al desenrollar los determinantes de estas matrices se obtiene la fórmula de Leibniz mencionada anteriormente. De manera similar, la expansión de Laplace a lo largo de la columna -ésima es la igualdad ${\displaystyle 2\times 2}$ ${\displaystyle j}$

${\displaystyle \det(A)=\sum _{i=1}^{n}(-1)^{i+j}a_{i,j}M_{i,j}.}$

La expansión de Laplace se puede utilizar iterativamente para calcular determinantes, pero este enfoque es ineficiente para matrices grandes. Sin embargo, es útil para calcular los determinantes de matrices altamente simétricas como la matriz de Vandermonde. La expansión de Laplace de n términos a lo largo de una fila o columna se puede generalizar para escribir un determinante n x n como una suma de términos , cada uno el producto del determinante de una submatriz k x k y el determinante de la submatriz complementaria ( n−k ) x ( n−k ). $${\displaystyle {\begin{vmatrix}1&1&1&\cdots &1\\x_{1}&x_{2}&x_{3}&\cdots &x_{n}\\x_{1}^{2}&x_{2}^{2}&x_{3}^{2}&\cdots &x_{n}^{2}\\\vdots &\vdots &\vdots &\ddots &\vdots \\x_{1}^{n-1}&x_{2}^{n-1}&x_{3}^{n-1}&\cdots &x_{n}^{n-1}\end{vmatrix}}=\prod _{1\leq i<j\leq n}\left(x_{j}-x_{i}\right).}$$ ${\displaystyle {\tbinom {n}{k}}}$

Matriz adjunta

La matriz adjunta es la transpuesta de la matriz de los cofactores, es decir, ${\displaystyle \operatorname {adj} (A)}$

${\displaystyle (\operatorname {adj} (A))_{i,j}=(-1)^{i+j}M_{ji}.}$

Para cada matriz, se tiene ^[11]

${\displaystyle (\det A)I=A\operatorname {adj} A=(\operatorname {adj} A)\,A.}$

Por lo tanto, la matriz adjunta se puede utilizar para expresar la inversa de una matriz no singular :

${\displaystyle A^{-1}={\frac {1}{\det A}}\operatorname {adj} A.}$

Matrices de bloques

La fórmula para el determinante de una matriz -descrita anteriormente sigue siendo válida, bajo supuestos adicionales apropiados, para una matriz de bloques , es decir, una matriz compuesta por cuatro submatrices de dimensión , , y , respectivamente. La fórmula más sencilla de este tipo, que se puede demostrar utilizando la fórmula de Leibniz o una factorización que involucre el complemento de Schur , es ${\displaystyle 2\times 2}$ ${\displaystyle A,B,C,D}$ ${\displaystyle m\times m}$ ${\displaystyle m\times n}$ ${\displaystyle n\times m}$ ${\displaystyle n\times n}$

${\displaystyle \det {\begin{pmatrix}A&0\\C&D\end{pmatrix}}=\det(A)\det(D)=\det {\begin{pmatrix}A&B\\0&D\end{pmatrix}}.}$

Si es invertible , entonces se deduce con los resultados de la sección sobre multiplicidad que ${\displaystyle A}$

${\displaystyle {\begin{aligned}\det {\begin{pmatrix}A&B\\C&D\end{pmatrix}}&=\det(A)\det {\begin{pmatrix}A&B\\C&D\end{pmatrix}}\underbrace {\det {\begin{pmatrix}A^{-1}&-A^{-1}B\\0&I_{n}\end{pmatrix}}} _{=\,\det(A^{-1})\,=\,(\det A)^{-1}}\\&=\det(A)\det {\begin{pmatrix}I_{m}&0\\CA^{-1}&D-CA^{-1}B\end{pmatrix}}\\&=\det(A)\det(D-CA^{-1}B),\end{aligned}}}$

lo cual se simplifica a cuando es una matriz. ${\displaystyle \det(A)(D-CA^{-1}B)}$ ${\displaystyle D}$ ${\displaystyle 1\times 1}$

Un resultado similar se cumple cuando es invertible, es decir ${\displaystyle D}$

${\displaystyle {\begin{aligned}\det {\begin{pmatrix}A&B\\C&D\end{pmatrix}}&=\det(D)\det {\begin{pmatrix}A&B\\C&D\end{pmatrix}}\underbrace {\det {\begin{pmatrix}I_{m}&0\\-D^{-1}C&D^{-1}\end{pmatrix}}} _{=\,\det(D^{-1})\,=\,(\det D)^{-1}}\\&=\det(D)\det {\begin{pmatrix}A-BD^{-1}C&BD^{-1}\\0&I_{n}\end{pmatrix}}\\&=\det(D)\det(A-BD^{-1}C).\end{aligned}}}$

Ambos resultados pueden combinarse para derivar el teorema del determinante de Sylvester , que también se enuncia a continuación.

Si los bloques son matrices cuadradas del mismo tamaño, se aplican otras fórmulas. Por ejemplo, si y conmutan (es decir, ), entonces ^[12] ${\displaystyle C}$ ${\displaystyle D}$ ${\displaystyle CD=DC}$

${\displaystyle \det {\begin{pmatrix}A&B\\C&D\end{pmatrix}}=\det(AD-BC).}$

Esta fórmula se ha generalizado a matrices compuestas de más de bloques, nuevamente bajo condiciones de conmutatividad apropiadas entre los bloques individuales. ^[13] ${\displaystyle 2\times 2}$

Para y , se cumple la siguiente fórmula (incluso si y no conmutan) ^{[ cita requerida ]} ${\displaystyle A=D}$ ${\displaystyle B=C}$ ${\displaystyle A}$ ${\displaystyle B}$

${\displaystyle \det {\begin{pmatrix}A&B\\B&A\end{pmatrix}}=\det(A-B)\det(A+B).}$

Teorema del determinante de Sylvester

El teorema del determinante de Sylvester establece que para A , una matriz m × n , y B , una matriz n × m (de modo que A y B tienen dimensiones que permiten multiplicarlos en cualquier orden formando una matriz cuadrada):

${\displaystyle \det \left(I_{\mathit {m}}+AB\right)=\det \left(I_{\mathit {n}}+BA\right),}$

donde I _m e I _n son las matrices identidad m × m y n × n , respectivamente.

De este resultado general se desprenden varias consecuencias.

1. Para el caso del vector columna c y el vector fila r , cada uno con m componentes, la fórmula permite el cálculo rápido del determinante de una matriz que difiere de la matriz identidad por una matriz de rango 1:

   ${\displaystyle \det \left(I_{\mathit {m}}+cr\right)=1+rc.}$

2. De manera más general, ^[14] para cualquier matriz invertible m × m X ,
   ${\displaystyle \det(X+AB)=\det(X)\det \left(I_{\mathit {n}}+BX^{-1}A\right),}$
3. Para un vector de columna y fila como el anterior:
   ${\displaystyle \det(X+cr)=\det(X)\det \left(1+rX^{-1}c\right)=\det(X)+r\,\operatorname {adj} (X)\,c.}$
4. Para matrices cuadradas y del mismo tamaño, las matrices y tienen los mismos polinomios característicos (por lo tanto, los mismos valores propios). ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle AB}$ ${\displaystyle BA}$

Suma

El determinante de la suma de dos matrices cuadradas del mismo tamaño no es en general expresable en términos de los determinantes de A y de B. ${\displaystyle A+B}$

Sin embargo, para matrices semidefinidas positivas y de igual tamaño, con el corolario ^[15] [ ^16] ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle C}$ $${\displaystyle \det(A+B+C)+\det(C)\geq \det(A+C)+\det(B+C){\text{,}}}$$ $${\displaystyle \det(A+B)\geq \det(A)+\det(B){\text{.}}}$$

El teorema de Brunn-Minkowski implica que la raíz n -ésima del determinante es una función cóncava , cuando se restringe a matrices hermíticas definidas positivas . ^[17] Por lo tanto, si A y B son matrices hermíticas definidas positivas , se tiene ya que la raíz n- ésima del determinante es una función homogénea . ${\displaystyle n\times n}$ ${\displaystyle n\times n}$ $${\displaystyle {\sqrt[{n}]{\det(A+B)}}\geq {\sqrt[{n}]{\det(A)}}+{\sqrt[{n}]{\det(B)}},}$$

Identidad de suma para matrices 2×2

Para el caso especial de matrices con entradas complejas, el determinante de la suma se puede escribir en términos de determinantes y trazas en la siguiente identidad: ${\displaystyle 2\times 2}$

${\displaystyle \det(A+B)=\det(A)+\det(B)+{\text{tr}}(A){\text{tr}}(B)-{\text{tr}}(AB).}$

Documentos de identidad

Esto se puede demostrar escribiendo cada término en componentes . El lado izquierdo es ${\displaystyle A_{ij},B_{ij}}$

${\displaystyle (A_{11}+B_{11})(A_{22}+B_{22})-(A_{12}+B_{12})(A_{21}+B_{21}).}$

La expansión da

${\displaystyle A_{11}A_{22}+B_{11}A_{22}+A_{11}B_{22}+B_{11}B_{22}-A_{12}A_{21}-B_{12}A_{21}-A_{12}B_{21}-B_{12}B_{21}.}$

Se ve que los términos que son cuadráticos en son , y de manera similar para , por lo que la expresión se puede escribir ${\displaystyle A}$ ${\displaystyle \det(A)}$ ${\displaystyle B}$

${\displaystyle \det(A)+\det(B)+A_{11}B_{22}+B_{11}A_{22}-A_{12}B_{21}-B_{12}A_{21}.}$

Podemos entonces escribir los términos cruzados como

${\displaystyle (A_{11}+A_{22})(B_{11}+B_{22})-(A_{11}B_{11}+A_{12}B_{21}+A_{21}B_{12}+A_{22}B_{22})}$

que puede reconocerse como

${\displaystyle {\text{tr}}(A){\text{tr}}(B)-{\text{tr}}(AB).}$

lo que completa la prueba.

Esto tiene una aplicación en las álgebras matriciales. Por ejemplo, considere los números complejos como un álgebra matricial. Los números complejos tienen una representación como matrices de la forma con y reales. Como , tomando y en la identidad anterior da ${\displaystyle 2\times 2}$ $${\displaystyle aI+b\mathbf {i} :=a{\begin{pmatrix}1&0\\0&1\end{pmatrix}}+b{\begin{pmatrix}0&-1\\1&0\end{pmatrix}}}$$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle {\text{tr}}(\mathbf {i} )=0}$ ${\displaystyle A=aI}$ ${\displaystyle B=b\mathbf {i} }$

${\displaystyle \det(aI+b\mathbf {i} )=a^{2}\det(I)+b^{2}\det(\mathbf {i} )=a^{2}+b^{2}.}$

Este resultado se dedujo simplemente de y . ${\displaystyle {\text{tr}}(\mathbf {i} )=0}$ ${\displaystyle \det(I)=\det(\mathbf {i} )=1}$

Propiedades del determinante en relación con otras nociones

Valores propios y polinomio característico

El determinante está estrechamente relacionado con otros dos conceptos centrales del álgebra lineal, los valores propios y el polinomio característico de una matriz. Sea una matriz con elementos complejos . Entonces, por el Teorema Fundamental del Álgebra, debe tener exactamente n valores propios . (Aquí se entiende que un valor propio con multiplicidad algebraica μ aparece μ veces en esta lista). Entonces, resulta que el determinante de A es igual al producto de estos valores propios, ${\displaystyle A}$ ${\displaystyle n\times n}$ ${\displaystyle A}$ ${\displaystyle \lambda _{1},\lambda _{2},\ldots ,\lambda _{n}}$

${\displaystyle \det(A)=\prod _{i=1}^{n}\lambda _{i}=\lambda _{1}\lambda _{2}\cdots \lambda _{n}.}$

El producto de todos los valores propios distintos de cero se denomina pseudodeterminante .

De esto se desprende inmediatamente que el determinante de una matriz es cero si y solo si es un valor propio de . En otras palabras, es invertible si y solo si no es un valor propio de . ${\displaystyle A}$ ${\displaystyle 0}$ ${\displaystyle A}$ ${\displaystyle A}$ ${\displaystyle 0}$ ${\displaystyle A}$

El polinomio característico se define como ^[18]

${\displaystyle \chi _{A}(t)=\det(t\cdot I-A).}$

Aquí, es la indeterminada del polinomio y es la matriz identidad del mismo tamaño que . Mediante este polinomio, se pueden utilizar los determinantes para hallar los valores propios de la matriz : son precisamente las raíces de este polinomio, es decir, aquellos números complejos tales que ${\displaystyle t}$ ${\displaystyle I}$ ${\displaystyle A}$ ${\displaystyle A}$ ${\displaystyle \lambda }$

${\displaystyle \chi _{A}(\lambda )=0.}$

Una matriz hermítica es definida positiva si todos sus valores propios son positivos. El criterio de Sylvester afirma que esto es equivalente a los determinantes de las submatrices.

${\displaystyle A_{k}:={\begin{bmatrix}a_{1,1}&a_{1,2}&\cdots &a_{1,k}\\a_{2,1}&a_{2,2}&\cdots &a_{2,k}\\\vdots &\vdots &\ddots &\vdots \\a_{k,1}&a_{k,2}&\cdots &a_{k,k}\end{bmatrix}}}$

siendo positivo, para todos entre y . ^[19] ${\displaystyle k}$ ${\displaystyle 1}$ ${\displaystyle n}$

Rastro

La traza tr( A ) es por definición la suma de las entradas diagonales de A y también es igual a la suma de los valores propios. Por lo tanto, para matrices complejas A ,

${\displaystyle \det(\exp(A))=\exp(\operatorname {tr} (A))}$

o, para matrices reales A ,

${\displaystyle \operatorname {tr} (A)=\log(\det(\exp(A))).}$

Aquí exp( A ) denota la matriz exponencial de A , porque cada valor propio λ de A corresponde al valor propio exp( λ ) de exp( A ). En particular, dado cualquier logaritmo de A , es decir, cualquier matriz L que satisfaga

${\displaystyle \exp(L)=A}$

El determinante de A viene dado por

${\displaystyle \det(A)=\exp(\operatorname {tr} (L)).}$

Por ejemplo, para n = 2 , n = 3 y n = 4 , respectivamente,

${\displaystyle {\begin{aligned}\det(A)&={\frac {1}{2}}\left(\left(\operatorname {tr} (A)\right)^{2}-\operatorname {tr} \left(A^{2}\right)\right),\\\det(A)&={\frac {1}{6}}\left(\left(\operatorname {tr} (A)\right)^{3}-3\operatorname {tr} (A)~\operatorname {tr} \left(A^{2}\right)+2\operatorname {tr} \left(A^{3}\right)\right),\\\det(A)&={\frac {1}{24}}\left(\left(\operatorname {tr} (A)\right)^{4}-6\operatorname {tr} \left(A^{2}\right)\left(\operatorname {tr} (A)\right)^{2}+3\left(\operatorname {tr} \left(A^{2}\right)\right)^{2}+8\operatorname {tr} \left(A^{3}\right)~\operatorname {tr} (A)-6\operatorname {tr} \left(A^{4}\right)\right).\end{aligned}}}$

cf. Teorema de Cayley-Hamilton . Tales expresiones son deducibles a partir de argumentos combinatorios, identidades de Newton o el algoritmo de Faddeev–LeVerrier . Es decir, para n genérico , det A = (−1) ⁿ c ₀ el término constante con signo del polinomio característico , determinado recursivamente a partir de

${\displaystyle c_{n}=1;~~~c_{n-m}=-{\frac {1}{m}}\sum _{k=1}^{m}c_{n-m+k}\operatorname {tr} \left(A^{k}\right)~~(1\leq m\leq n)~.}$

En el caso general, esto también se puede obtener de ^[20].

${\displaystyle \det(A)=\sum _{\begin{array}{c}k_{1},k_{2},\ldots ,k_{n}\geq 0\\k_{1}+2k_{2}+\cdots +nk_{n}=n\end{array}}\prod _{l=1}^{n}{\frac {(-1)^{k_{l}+1}}{l^{k_{l}}k_{l}!}}\operatorname {tr} \left(A^{l}\right)^{k_{l}},}$

donde la suma se toma sobre el conjunto de todos los números enteros k _l ≥ 0 que satisfacen la ecuación

${\displaystyle \sum _{l=1}^{n}lk_{l}=n.}$

La fórmula se puede expresar en términos del polinomio de Bell exponencial completo de n argumentos s _l = −( l – 1)! tr( A ^l ) como

${\displaystyle \det(A)={\frac {(-1)^{n}}{n!}}B_{n}(s_{1},s_{2},\ldots ,s_{n}).}$

Esta fórmula también se puede utilizar para hallar el determinante de una matriz A ^I _J con índices multidimensionales I = ( i ₁ , i ₂ , ..., i _r ) y J = ( j ₁ , j ₂ , ..., j _r ) . El producto y la traza de dichas matrices se definen de forma natural como

${\displaystyle (AB)_{J}^{I}=\sum _{K}A_{K}^{I}B_{J}^{K},\operatorname {tr} (A)=\sum _{I}A_{I}^{I}.}$

Se puede obtener una identidad n de dimensión arbitraria importante a partir de la expansión en serie de Mercator del logaritmo cuando la expansión converge. Si cada valor propio de A es menor que 1 en valor absoluto,

${\displaystyle \det(I+A)=\sum _{k=0}^{\infty }{\frac {1}{k!}}\left(-\sum _{j=1}^{\infty }{\frac {(-1)^{j}}{j}}\operatorname {tr} \left(A^{j}\right)\right)^{k}\,,}$

donde I es la matriz identidad. De manera más general, si

${\displaystyle \sum _{k=0}^{\infty }{\frac {1}{k!}}\left(-\sum _{j=1}^{\infty }{\frac {(-1)^{j}s^{j}}{j}}\operatorname {tr} \left(A^{j}\right)\right)^{k}\,,}$

se expande como una serie de potencia formal en s, entonces todos los coeficientes de s ^m para m > n son cero y el polinomio restante es det( I + sA ) .

Límites superior e inferior

Para una matriz definida positiva A , el operador de traza proporciona los siguientes límites inferior y superior estrictos en el determinante logarítmico

${\displaystyle \operatorname {tr} \left(I-A^{-1}\right)\leq \log \det(A)\leq \operatorname {tr} (A-I)}$

con igualdad si y sólo si A = I . Esta relación se puede derivar mediante la fórmula para la divergencia de Kullback-Leibler entre dos distribuciones normales multivariadas .

También,

${\displaystyle {\frac {n}{\operatorname {tr} \left(A^{-1}\right)}}\leq \det(A)^{\frac {1}{n}}\leq {\frac {1}{n}}\operatorname {tr} (A)\leq {\sqrt {{\frac {1}{n}}\operatorname {tr} \left(A^{2}\right)}}.}$

Estas desigualdades se pueden demostrar expresando las trazas y el determinante en términos de los valores propios. Como tales, representan el hecho bien conocido de que la media armónica es menor que la media geométrica , que es menor que la media aritmética , que es, a su vez, menor que la raíz cuadrada media .

Derivado

La fórmula de Leibniz muestra que el determinante de matrices cuadradas reales (o análogamente para matrices complejas) es una función polinómica de a . En particular, es diferenciable en todas partes . Su derivada puede expresarse utilizando la fórmula de Jacobi : ^[21] ${\displaystyle \mathbf {R} ^{n\times n}}$ ${\displaystyle \mathbf {R} }$

${\displaystyle {\frac {d\det(A)}{d\alpha }}=\operatorname {tr} \left(\operatorname {adj} (A){\frac {dA}{d\alpha }}\right).}$

donde denota el adjutor de . En particular, si es invertible, tenemos ${\displaystyle \operatorname {adj} (A)}$ ${\displaystyle A}$ ${\displaystyle A}$

${\displaystyle {\frac {d\det(A)}{d\alpha }}=\det(A)\operatorname {tr} \left(A^{-1}{\frac {dA}{d\alpha }}\right).}$

Expresados ​​en términos de las entradas de , estos son ${\displaystyle A}$

${\displaystyle {\frac {\partial \det(A)}{\partial A_{ij}}}=\operatorname {adj} (A)_{ji}=\det(A)\left(A^{-1}\right)_{ji}.}$

Otra formulación equivalente es

${\displaystyle \det(A+\epsilon X)-\det(A)=\operatorname {tr} (\operatorname {adj} (A)X)\epsilon +O\left(\epsilon ^{2}\right)=\det(A)\operatorname {tr} \left(A^{-1}X\right)\epsilon +O\left(\epsilon ^{2}\right)}$,

utilizando la notación O grande . El caso especial donde , la matriz identidad, produce ${\displaystyle A=I}$

${\displaystyle \det(I+\epsilon X)=1+\operatorname {tr} (X)\epsilon +O\left(\epsilon ^{2}\right).}$

Esta identidad se utiliza para describir álgebras de Lie asociadas a ciertos grupos de Lie de matrices . Por ejemplo, el grupo lineal especial se define mediante la ecuación . La fórmula anterior muestra que su álgebra de Lie es el álgebra de Lie lineal especial que consiste en aquellas matrices que tienen traza cero. ${\displaystyle \operatorname {SL} _{n}}$ ${\displaystyle \det A=1}$ ${\displaystyle {\mathfrak {sl}}_{n}}$

Al escribir una matriz como donde son vectores columna de longitud 3, entonces el gradiente sobre uno de los tres vectores puede escribirse como el producto vectorial de los otros dos: ${\displaystyle 3\times 3}$ ${\displaystyle A={\begin{bmatrix}a&b&c\end{bmatrix}}}$ ${\displaystyle a,b,c}$

${\displaystyle {\begin{aligned}\nabla _{\mathbf {a} }\det(A)&=\mathbf {b} \times \mathbf {c} \\\nabla _{\mathbf {b} }\det(A)&=\mathbf {c} \times \mathbf {a} \\\nabla _{\mathbf {c} }\det(A)&=\mathbf {a} \times \mathbf {b} .\end{aligned}}}$

Historia

Históricamente, los determinantes se utilizaron mucho antes que las matrices: un determinante se definió originalmente como una propiedad de un sistema de ecuaciones lineales . El determinante "determina" si el sistema tiene una solución única (lo que ocurre precisamente si el determinante no es cero). En este sentido, los determinantes se utilizaron por primera vez en el libro de texto de matemáticas chino Los nueve capítulos sobre el arte matemático (九章算術, eruditos chinos, alrededor del siglo III a. C.). En Europa, las soluciones de sistemas lineales de dos ecuaciones fueron expresadas por Cardano en 1545 mediante una entidad similar a un determinante. ^[22]

Los determinantes propiamente dichos se originaron por separado a partir del trabajo de Seki Takakazu en 1683 en Japón y paralelamente de Leibniz en 1693. ^{[23] [24] [25] [26]} Cramer (1750) enunció, sin prueba, la regla de Cramer. ^[27] Tanto Cramer como Bézout (1779) fueron llevados a los determinantes por la cuestión de las curvas planas que pasan por un conjunto dado de puntos. ^[28]

Vandermonde (1771) fue el primero en reconocer los determinantes como funciones independientes. ^[24] Laplace (1772) dio el método general para desarrollar un determinante en términos de sus menores complementarios : Vandermonde ya había dado un caso especial. ^[29] Inmediatamente después, Lagrange (1773) trató los determinantes de segundo y tercer orden y los aplicó a cuestiones de teoría de eliminación ; demostró muchos casos especiales de identidades generales.

Gauss (1801) realizó el siguiente avance. Al igual que Lagrange, hizo un gran uso de los determinantes en la teoría de números . Introdujo la palabra "determinante" (Laplace había usado "resultante"), aunque no en el significado actual, sino más bien como se aplica al discriminante de un cuanto . ^[30] Gauss también llegó a la noción de determinantes recíprocos (inversos) y se acercó mucho al teorema de la multiplicación. ^{[ aclaración necesaria ]}

El siguiente autor de importancia fue Binet (1811, 1812), quien enunció formalmente el teorema relativo al producto de dos matrices de m columnas y n filas, que para el caso especial de m = n se reduce al teorema de la multiplicación. El mismo día (30 de noviembre de 1812) en que Binet presentó su trabajo en la Academia, Cauchy también presentó uno sobre el tema (véase la fórmula de Cauchy-Binet ). En él utilizó la palabra "determinante" en su sentido actual, ^{[31] [32]} resumió y simplificó lo que se sabía entonces sobre el tema, mejoró la notación y presentó el teorema de la multiplicación con una prueba más satisfactoria que la de Binet. ^{[24] [33]} Con él comienza la teoría en su generalidad.

Jacobi (1841) utilizó el determinante funcional que Sylvester más tarde llamó jacobiano . ^[34] En sus memorias en el Crelle's Journal de 1841, trata especialmente este tema, así como la clase de funciones alternantes que Sylvester ha llamado alternantes . En la época de las últimas memorias de Jacobi, Sylvester (1839) y Cayley comenzaron su trabajo. Cayley en 1841 introdujo la notación moderna para el determinante utilizando barras verticales. ^{[35] [36]}

El estudio de las formas especiales de los determinantes ha sido el resultado natural de la finalización de la teoría general. Los determinantes axisimétricos han sido estudiados por Lebesgue , Hesse y Sylvester; los determinantes persimétricos por Sylvester y Hankel ; los circulantes por Catalan , Spottiswoode , Glaisher y Scott; los determinantes oblicuos y pfaffianos , en conexión con la teoría de la transformación ortogonal , por Cayley; los continuantes por Sylvester; los wronskianos (así llamados por Muir ) por Christoffel y Frobenius ; los determinantes compuestos por Sylvester, Reiss y Picquet; los jacobianos y hessianos por Sylvester; y los determinantes simétricos gauche por Trudi . De los libros de texto sobre el tema, el de Spottiswoode fue el primero. En Estados Unidos, Hanus (1886), Weld (1893) y Muir/Metzler (1933) publicaron tratados.

Aplicaciones

Regla de Cramer

Los determinantes se pueden utilizar para describir las soluciones de un sistema lineal de ecuaciones , escrito en forma matricial como . Esta ecuación tiene una solución única si y solo si es distinto de cero. En este caso, la solución viene dada por la regla de Cramer : ${\displaystyle Ax=b}$ ${\displaystyle x}$ ${\displaystyle \det(A)}$

${\displaystyle x_{i}={\frac {\det(A_{i})}{\det(A)}}\qquad i=1,2,3,\ldots ,n}$

donde es la matriz formada al reemplazar la -ésima columna de por el vector columna . Esto sigue inmediatamente por la expansión en columna del determinante, es decir ${\displaystyle A_{i}}$ ${\displaystyle i}$ ${\displaystyle A}$ ${\displaystyle b}$

${\displaystyle \det(A_{i})=\det {\begin{bmatrix}a_{1}&\ldots &b&\ldots &a_{n}\end{bmatrix}}=\sum _{j=1}^{n}x_{j}\det {\begin{bmatrix}a_{1}&\ldots &a_{i-1}&a_{j}&a_{i+1}&\ldots &a_{n}\end{bmatrix}}=x_{i}\det(A)}$

donde los vectores son las columnas de A . La regla también está implícita en la identidad ${\displaystyle a_{j}}$

${\displaystyle A\,\operatorname {adj} (A)=\operatorname {adj} (A)\,A=\det(A)\,I_{n}.}$

La regla de Cramer se puede implementar en el tiempo, lo que es comparable a los métodos más comunes de resolución de sistemas de ecuaciones lineales, como LU , QR o la descomposición en valores singulares . ^[37] ${\displaystyle \operatorname {O} (n^{3})}$

Independencia lineal

Los determinantes se pueden utilizar para caracterizar vectores linealmente dependientes : es cero si y solo si los vectores columna (o, equivalentemente, los vectores fila) de la matriz son linealmente dependientes. ^[38] Por ejemplo, dados dos vectores linealmente independientes , un tercer vector se encuentra en el plano generado por los dos vectores anteriores exactamente si el determinante de la matriz - que consiste en los tres vectores es cero. La misma idea también se utiliza en la teoría de ecuaciones diferenciales : dadas funciones (supuestamente diferenciables ), el wronskiano se define como ${\displaystyle \det A}$ ${\displaystyle A}$ ${\displaystyle v_{1},v_{2}\in \mathbf {R} ^{3}}$ ${\displaystyle v_{3}}$ ${\displaystyle 3\times 3}$ ${\displaystyle f_{1}(x),\dots ,f_{n}(x)}$ ${\displaystyle n-1}$

${\displaystyle W(f_{1},\ldots ,f_{n})(x)={\begin{vmatrix}f_{1}(x)&f_{2}(x)&\cdots &f_{n}(x)\\f_{1}'(x)&f_{2}'(x)&\cdots &f_{n}'(x)\\\vdots &\vdots &\ddots &\vdots \\f_{1}^{(n-1)}(x)&f_{2}^{(n-1)}(x)&\cdots &f_{n}^{(n-1)}(x)\end{vmatrix}}.}$

Es distinto de cero (para algún ) en un intervalo especificado si y solo si las funciones dadas y todas sus derivadas hasta el orden son linealmente independientes. Si se puede demostrar que el wronskiano es cero en todas partes en un intervalo, entonces, en el caso de funciones analíticas , esto implica que las funciones dadas son linealmente dependientes. Véase el wronskiano y la independencia lineal . Otro uso similar del determinante es la resultante , que da un criterio cuando dos polinomios tienen una raíz común . ^[39] ${\displaystyle x}$ ${\displaystyle n-1}$

Orientación de una base

El determinante puede considerarse como la asignación de un número a cada secuencia de n vectores en R ⁿ , utilizando la matriz cuadrada cuyas columnas son los vectores dados. El determinante será distinto de cero si y solo si la secuencia de vectores es una base para R ⁿ . En ese caso, el signo del determinante determina si la orientación de la base es consistente con o opuesta a la orientación de la base estándar . En el caso de una base ortogonal, la magnitud del determinante es igual al producto de las longitudes de los vectores de la base. Por ejemplo, una matriz ortogonal con entradas en R ⁿ representa una base ortonormal en el espacio euclidiano , y por lo tanto tiene un determinante de ±1 (ya que todos los vectores tienen una longitud de 1). El determinante es +1 si y solo si la base tiene la misma orientación. Es −1 si y solo si la base tiene la orientación opuesta.

De manera más general, si el determinante de A es positivo, A representa una transformación lineal que preserva la orientación (si A es una matriz ortogonal 2 × 2 o 3 × 3 , esto es una rotación ), mientras que si es negativo, A cambia la orientación de la base.

Volumen y determinante jacobiano

Como se señaló anteriormente, el valor absoluto del determinante de los vectores reales es igual al volumen del paralelepípedo abarcado por esos vectores. En consecuencia, si es la función lineal dada por la multiplicación con una matriz , y es cualquier subconjunto medible , entonces el volumen de está dado por multiplicado por el volumen de . ^[40] De manera más general, si la función lineal está representada por la matriz - , entonces el volumen - dimensional de está dado por: ${\displaystyle f:\mathbf {R} ^{n}\to \mathbf {R} ^{n}}$ ${\displaystyle A}$ ${\displaystyle S\subset \mathbf {R} ^{n}}$ ${\displaystyle f(S)}$ ${\displaystyle |\det(A)|}$ ${\displaystyle S}$ ${\displaystyle f:\mathbf {R} ^{n}\to \mathbf {R} ^{m}}$ ${\displaystyle m\times n}$ ${\displaystyle A}$ ${\displaystyle n}$ ${\displaystyle f(S)}$

${\displaystyle \operatorname {volume} (f(S))={\sqrt {\det \left(A^{\textsf {T}}A\right)}}\operatorname {volume} (S).}$

Calculando el volumen del tetraedro acotado por cuatro puntos, se pueden utilizar para identificar líneas oblicuas . El volumen de cualquier tetraedro, dados sus vértices , , o cualquier otra combinación de pares de vértices que formen un árbol de expansión sobre los vértices. ${\displaystyle a,b,c,d}$ ${\displaystyle {\frac {1}{6}}\cdot |\det(a-b,b-c,c-d)|}$

Una función no lineal envía un cuadrado pequeño (izquierda, en rojo) a un paralelogramo distorsionado (derecha, en rojo). El jacobiano en un punto proporciona la mejor aproximación lineal del paralelogramo distorsionado cerca de ese punto (derecha, en blanco translúcido), y el determinante jacobiano proporciona la relación entre el área del paralelogramo que se aproxima y la del cuadrado original. ${\displaystyle f\colon \mathbf {R} ^{2}\to \mathbf {R} ^{2}}$

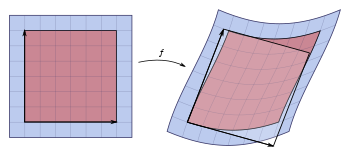
Para una función diferenciable general , gran parte de lo anterior se aplica considerando la matriz jacobiana de f .

${\displaystyle f:\mathbf {R} ^{n}\rightarrow \mathbf {R} ^{n},}$

La matriz jacobiana es la matriz n × n cuyas entradas están dadas por las derivadas parciales

${\displaystyle D(f)=\left({\frac {\partial f_{i}}{\partial x_{j}}}\right)_{1\leq i,j\leq n}.}$

Su determinante, el determinante jacobiano , aparece en la versión de dimensión superior de la integración por sustitución : para funciones adecuadas f y un subconjunto abierto U de R ⁿ (el dominio de f ), la integral sobre f ( U ) de alguna otra función φ  : R ⁿ → R ^m está dada por

${\displaystyle \int _{f(U)}\phi (\mathbf {v} )\,d\mathbf {v} =\int _{U}\phi (f(\mathbf {u} ))\left|\det(\operatorname {D} f)(\mathbf {u} )\right|\,d\mathbf {u} .}$

El jacobiano también aparece en el teorema de la función inversa .

Cuando se aplica al campo de la cartografía , el determinante se puede utilizar para medir la tasa de expansión de un mapa cerca de los polos. ^[41]

Aspectos algebraicos abstractos

Determinante de un endomorfismo

Las identidades anteriores relativas al determinante de productos e inversas de matrices implican que matrices similares tienen el mismo determinante: dos matrices A y B son similares, si existe una matriz invertible X tal que A = X ⁻¹ BX . De hecho, al aplicar repetidamente las identidades anteriores se obtiene

${\displaystyle \det(A)=\det(X)^{-1}\det(B)\det(X)=\det(B)\det(X)^{-1}\det(X)=\det(B).}$

Por lo tanto, el determinante también se denomina invariante de semejanza . El determinante de una transformación lineal

${\displaystyle T:V\to V}$

para un espacio vectorial de dimensión finita, V se define como el determinante de la matriz que lo describe, con respecto a una elección arbitraria de base en V. Por la invariancia de similitud, este determinante es independiente de la elección de la base para V y, por lo tanto , solo depende del endomorfismo T.

Matrices cuadradas sobre anillos conmutativos

La definición anterior del determinante utilizando la regla de Leibniz funciona de manera más general cuando las entradas de la matriz son elementos de un anillo conmutativo , como los números enteros , en oposición al cuerpo de números reales o complejos. Además, la caracterización del determinante como la única función multilineal alternada que satisface sigue siendo válida, al igual que todas las propiedades que resultan de esa caracterización. ^[42] ${\displaystyle R}$ ${\displaystyle \mathbf {Z} }$ ${\displaystyle \det(I)=1}$

Una matriz es invertible (en el sentido de que existe una matriz inversa cuyas entradas están en ) si y solo si su determinante es un elemento invertible en . ^[43] Para , esto significa que el determinante es +1 o −1. Una matriz de este tipo se denomina unimodular . ${\displaystyle A\in \operatorname {Mat} _{n\times n}(R)}$ ${\displaystyle R}$ ${\displaystyle R}$ ${\displaystyle R=\mathbf {Z} }$

El determinante es multiplicativo, por lo que define un homomorfismo de grupo.

${\displaystyle \operatorname {GL} _{n}(R)\rightarrow R^{\times },}$

entre el grupo lineal general (el grupo de matrices invertibles con entradas en ) y el grupo multiplicativo de unidades en . Dado que respeta la multiplicación en ambos grupos, esta función es un homomorfismo de grupo . ${\displaystyle n\times n}$ ${\displaystyle R}$ ${\displaystyle R}$

El determinante es una transformación natural.

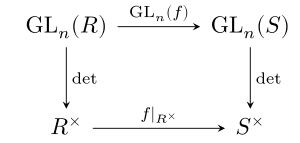
Dado un homomorfismo de anillo , existe una función dada al reemplazar todas las entradas en por sus imágenes bajo . El determinante respeta estas funciones, es decir, la identidad ${\displaystyle f:R\to S}$ ${\displaystyle \operatorname {GL} _{n}(f):\operatorname {GL} _{n}(R)\to \operatorname {GL} _{n}(S)}$ ${\displaystyle R}$ ${\displaystyle f}$

${\displaystyle f(\det((a_{i,j})))=\det((f(a_{i,j})))}$

se cumple. En otras palabras, el diagrama conmutativo mostrado conmuta.

Por ejemplo, el determinante del conjugado complejo de una matriz compleja (que también es el determinante de su transpuesta conjugada) es el conjugado complejo de su determinante, y para matrices enteras: el módulo de reducción del determinante de dicha matriz es igual al determinante de la matriz módulo reducido (el último determinante se calcula utilizando aritmética modular ). En el lenguaje de la teoría de categorías , el determinante es una transformación natural entre los dos funtores y . ^[44] Añadiendo otra capa de abstracción, esto se captura diciendo que el determinante es un morfismo de grupos algebraicos , desde el grupo lineal general hasta el grupo multiplicativo , ${\displaystyle m}$ ${\displaystyle m}$ ${\displaystyle \operatorname {GL} _{n}}$ ${\displaystyle (-)^{\times }}$

${\displaystyle \det :\operatorname {GL} _{n}\to \mathbb {G} _{m}.}$

Álgebra exterior

El determinante de una transformación lineal de un espacio vectorial de dimensión - o, más generalmente, un módulo libre de rango (finito) sobre un anillo conmutativo se puede formular de manera libre de coordenadas considerando la -ésima potencia exterior de . ^[45] La función induce una función lineal ${\displaystyle T:V\to V}$ ${\displaystyle n}$ ${\displaystyle V}$ ${\displaystyle n}$ ${\displaystyle R}$ ${\displaystyle n}$ ${\displaystyle \bigwedge ^{n}V}$ ${\displaystyle V}$ ${\displaystyle T}$

${\displaystyle {\begin{aligned}\bigwedge ^{n}T:\bigwedge ^{n}V&\rightarrow \bigwedge ^{n}V\\v_{1}\wedge v_{2}\wedge \dots \wedge v_{n}&\mapsto Tv_{1}\wedge Tv_{2}\wedge \dots \wedge Tv_{n}.\end{aligned}}}$

Como es unidimensional, la función se obtiene multiplicando por algún escalar, es decir, un elemento de . Algunos autores como (Bourbaki 1998) utilizan este hecho para definir el determinante como el elemento de que satisface la siguiente identidad (para todo ): ${\displaystyle \bigwedge ^{n}V}$ ${\displaystyle \bigwedge ^{n}T}$ ${\displaystyle R}$ ${\displaystyle R}$ ${\displaystyle v_{i}\in V}$

${\displaystyle \left(\bigwedge ^{n}T\right)\left(v_{1}\wedge \dots \wedge v_{n}\right)=\det(T)\cdot v_{1}\wedge \dots \wedge v_{n}.}$

Esta definición concuerda con la definición más concreta dependiente de coordenadas. Esto se puede demostrar utilizando la unicidad de una forma alternada multilineal en -tuplas de vectores en . Por esta razón, la potencia exterior no nula más alta (a diferencia del determinante asociado a un endomorfismo) a veces también se denomina determinante de y de manera similar para objetos más complejos como fibrados vectoriales o complejos en cadena de espacios vectoriales. Los menores de una matriz también se pueden convertir en este contexto, considerando formas alternadas inferiores con . ^[46] ${\displaystyle n}$ ${\displaystyle R^{n}}$ ${\displaystyle \bigwedge ^{n}V}$ ${\displaystyle V}$ ${\displaystyle \bigwedge ^{k}V}$ ${\displaystyle k<n}$

Generalizaciones y nociones relacionadas

Los determinantes tratados anteriormente admiten varias variantes: el permanente de una matriz se define como determinante, excepto que se omiten los factores que aparecen en la regla de Leibniz. El inmanente generaliza ambos introduciendo un carácter del grupo simétrico en la regla de Leibniz. ${\displaystyle \operatorname {sgn}(\sigma )}$ ${\displaystyle S_{n}}$

Determinantes para álgebras de dimensión finita

Para cualquier álgebra asociativa que sea de dimensión finita como un espacio vectorial sobre un cuerpo , existe un mapa determinante ^[47] ${\displaystyle A}$ ${\displaystyle F}$

${\displaystyle \det :A\to F.}$

Esta definición parte del establecimiento del polinomio característico independientemente del determinante y define el determinante como el término de menor orden de este polinomio. Esta definición general recupera el determinante para el álgebra matricial , pero también incluye varios casos más, entre ellos el determinante de un cuaternión . ${\displaystyle A=\operatorname {Mat} _{n\times n}(F)}$

${\displaystyle \det(a+ib+jc+kd)=a^{2}+b^{2}+c^{2}+d^{2}}$,

La norma de una extensión de campo , así como el Pfaffian de una matriz antisimétrica y la norma reducida de un álgebra central simple , también surgen como casos especiales de esta construcción. ${\displaystyle N_{L/F}:L\to F}$

Matrices infinitas

En el caso de matrices con un número infinito de filas y columnas, las definiciones anteriores del determinante no se aplican directamente. Por ejemplo, en la fórmula de Leibniz, se debería calcular una suma infinita (cuyos términos son todos productos infinitos). El análisis funcional proporciona distintas extensiones del determinante para este tipo de situaciones de dimensión infinita, que, sin embargo, solo funcionan para determinados tipos de operadores.

El determinante de Fredholm define el determinante para los operadores conocidos como operadores de clase traza mediante una generalización apropiada de la fórmula

${\displaystyle \det(I+A)=\exp(\operatorname {tr} (\log(I+A))).}$

Otra noción de determinante de dimensión infinita es el determinante funcional .

Operadores en álgebras de von Neumann

Para los operadores en un factor finito , se puede definir un determinante positivo de valor real llamado determinante de Fuglede−Kadison utilizando la traza canónica. De hecho, para cada estado de la traza en un álgebra de von Neumann existe una noción de determinante de Fuglede−Kadison.

Nociones relacionadas con anillos no conmutativos

Para matrices sobre anillos no conmutativos, la multilinealidad y las propiedades alternas son incompatibles para n ≥ 2 , ^[48] por lo que no existe una buena definición del determinante en este contexto.

Para matrices cuadradas con entradas en un anillo no conmutativo, existen varias dificultades para definir determinantes de manera análoga a la de los anillos conmutativos. Se puede dar un significado a la fórmula de Leibniz siempre que se especifique el orden del producto, y de manera similar para otras definiciones del determinante, pero la no conmutatividad conduce entonces a la pérdida de muchas propiedades fundamentales del determinante, como la propiedad multiplicativa o que el determinante no cambia bajo la transposición de la matriz. Sobre anillos no conmutativos, no hay una noción razonable de una forma multilineal (la existencia de una forma bilineal distinta de cero ^{[ aclarar ]} con un elemento regular de R como valor en algún par de argumentos implica que R es conmutativo). Sin embargo, se han formulado varias nociones de determinante no conmutativo que preservan algunas de las propiedades de los determinantes, en particular los cuasideterminantes y el determinante de Dieudonné . Para algunas clases de matrices con elementos no conmutativos, se puede definir el determinante y demostrar teoremas de álgebra lineal que son muy similares a sus análogos conmutativos. Los ejemplos incluyen el determinante q en grupos cuánticos, el determinante de Capelli en matrices de Capelli y el bereziniano en supermatrices (es decir, matrices cuyas entradas son elementos de anillos graduados ) . ^[49] Las matrices de Manin forman la clase más cercana a las matrices con elementos conmutativos. ${\displaystyle \mathbb {Z} _{2}}$

Cálculo

Los determinantes se utilizan principalmente como una herramienta teórica. Rara vez se calculan explícitamente en álgebra lineal numérica , donde para aplicaciones como la comprobación de la invertibilidad y la búsqueda de valores propios, el determinante ha sido reemplazado en gran medida por otras técnicas. ^{[50] Sin embargo,} la geometría computacional utiliza con frecuencia cálculos relacionados con los determinantes. ^[51]

Si bien el determinante se puede calcular directamente utilizando la regla de Leibniz, este enfoque es extremadamente ineficiente para matrices grandes, ya que esa fórmula requiere calcular productos ( factoriales ) para una matriz . Por lo tanto, el número de operaciones requeridas crece muy rápidamente: es del orden de . La expansión de Laplace es igualmente ineficiente. Por lo tanto, se han desarrollado técnicas más complejas para calcular determinantes. ${\displaystyle n!}$ ${\displaystyle n}$ ${\displaystyle n\times n}$ ${\displaystyle n!}$

Eliminación gaussiana

La eliminación gaussiana consiste en multiplicar por la izquierda una matriz por matrices elementales para obtener una matriz en forma escalonada . Se puede restringir el cálculo a matrices elementales de determinante 1. En este caso, el determinante de la forma escalonada resultante es igual al determinante de la matriz inicial. Como una forma escalonada es una matriz triangular , su determinante es el producto de los elementos de su diagonal.

Por lo tanto, el determinante se puede calcular casi gratis a partir del resultado de una eliminación gaussiana.

Métodos de descomposición

Algunos métodos calculan escribiendo la matriz como un producto de matrices cuyos determinantes se pueden calcular más fácilmente. Dichas técnicas se conocen como métodos de descomposición. Algunos ejemplos incluyen la descomposición LU , la descomposición QR o la descomposición de Cholesky (para matrices definidas positivas ). Estos métodos son del orden de , lo que supone una mejora significativa con respecto a . ^[52] ${\displaystyle \det(A)}$ ${\displaystyle \operatorname {O} (n^{3})}$ ${\displaystyle \operatorname {O} (n!)}$

Por ejemplo, la descomposición LU se expresa como un producto ${\displaystyle A}$

${\displaystyle A=PLU.}$

de una matriz de permutación (que tiene exactamente un solo en cada columna y ceros en el resto), una matriz triangular inferior y una matriz triangular superior . Los determinantes de las dos matrices triangulares y se pueden calcular rápidamente, ya que son los productos de las entradas diagonales respectivas. El determinante de es simplemente el signo de la permutación correspondiente (que es para un número par de permutaciones y es para un número impar de permutaciones). Una vez que se conoce dicha descomposición LU para , su determinante se calcula fácilmente como ${\displaystyle P}$ ${\displaystyle 1}$ ${\displaystyle L}$ ${\displaystyle U}$ ${\displaystyle L}$ ${\displaystyle U}$ ${\displaystyle P}$ ${\displaystyle \varepsilon }$ ${\displaystyle +1}$ ${\displaystyle -1}$ ${\displaystyle A}$

${\displaystyle \det(A)=\varepsilon \det(L)\cdot \det(U).}$

Otros métodos

El orden alcanzado por los métodos de descomposición se ha mejorado mediante diferentes métodos. Si dos matrices de orden se pueden multiplicar en tiempo , donde para algún , entonces existe un algoritmo que calcula el determinante en tiempo . ^[53] Esto significa, por ejemplo, que existe un algoritmo para calcular el determinante basado en el algoritmo Coppersmith–Winograd . Este exponente se ha reducido aún más, a partir de 2016, a 2,373. ^[54] ${\displaystyle \operatorname {O} (n^{3})}$ ${\displaystyle n}$ ${\displaystyle M(n)}$ ${\displaystyle M(n)\geq n^{a}}$ ${\displaystyle a>2}$ ${\displaystyle O(M(n))}$ ${\displaystyle \operatorname {O} (n^{2.376})}$

Además de la complejidad del algoritmo, se pueden utilizar otros criterios para comparar algoritmos. Especialmente para aplicaciones relacionadas con matrices sobre anillos, existen algoritmos que calculan el determinante sin ninguna división. (Por el contrario, la eliminación de Gauss requiere divisiones). Uno de estos algoritmos, que tiene complejidad, se basa en la siguiente idea: uno reemplaza permutaciones (como en la regla de Leibniz) por los llamados paseos ordenados cerrados, en los que se pueden repetir varios elementos. La suma resultante tiene más términos que en la regla de Leibniz, pero en el proceso se pueden reutilizar varios de estos productos, lo que lo hace más eficiente que el cálculo ingenuo con la regla de Leibniz. ^[55] Los algoritmos también se pueden evaluar de acuerdo con su complejidad de bits , es decir, cuántos bits de precisión se necesitan para almacenar valores intermedios que ocurren en el cálculo. Por ejemplo, el método de eliminación gaussiana (o descomposición LU) es de orden , pero la longitud de bits de los valores intermedios puede llegar a ser exponencialmente larga. ^[56] En comparación, el algoritmo de Bareiss , es un método de división exacta (por lo que utiliza división, pero solo en casos donde estas divisiones se pueden realizar sin resto) es del mismo orden, pero la complejidad de bits es aproximadamente el tamaño de bits de las entradas originales en la matriz multiplicada por . ^[57] ${\displaystyle \operatorname {O} (n^{4})}$ ${\displaystyle \operatorname {O} (n^{3})}$ ${\displaystyle n}$

Si ya se han calculado el determinante de A y la inversa de A , el lema del determinante matricial permite un cálculo rápido del determinante de A + uv ^T , donde u y v son vectores columna.

Charles Dodgson (es decir, Lewis Carroll, famoso por su libro Alicia en el país de las maravillas ) inventó un método para calcular determinantes llamado condensación de Dodgson . Lamentablemente, este interesante método no siempre funciona en su forma original. ^[58]

Véase también

• Portal de matemáticas

• Determinante de Cauchy
• Determinante de Cayley-Menger
• Determinante de Dieudonné
• Determinante de Slater
• Conjetura determinante

Notas

1. Lang 1985, §VII.1
2. Wildberger, Norman J. (2010). Episodio 4 (conferencia en video). WildLinAlg. Sídney, Australia: Universidad de Nueva Gales del Sur . Archivado desde el original el 11 de diciembre de 2021 – vía YouTube.
3. "Determinantes y volúmenes". textbooks.math.gatech.edu . Consultado el 16 de marzo de 2018 .
4. McConnell (1957). Aplicaciones del análisis tensorial . Publicaciones de Dover. Págs. 10-17.
5. Harris 2014, §4.7
6. Serge Lang , Álgebra lineal , 2.ª edición, Addison-Wesley, 1971, págs. 173, 191.
7. Lang 1987, §VI.7, Teorema 7.5
8. Alternativamente, Bourbaki 1998, §III.8, Proposición 1 prueba este resultado utilizando la funcionalidad del poder exterior.
9. Horn y Johnson 2018, §0.8.7
10. Kung, Rota y Yan 2009, pág. 306
11. Horn y Johnson 2018, §0.8.2.
12. Silvester, JR (2000). "Determinantes de matrices de bloques". Math. Gaz . 84 (501): 460–467. doi :10.2307/3620776. JSTOR  3620776. S2CID  41879675.
13. Sothanaphan, Nat (enero de 2017). "Determinantes de matrices de bloques con bloques no conmutativos". Álgebra lineal y sus aplicaciones . 512 : 202–218. arXiv : 1805.06027 . doi :10.1016/j.laa.2016.10.004. S2CID  119272194.
14. Las pruebas se pueden encontrar en http://www.ee.ic.ac.uk/hp/staff/dmb/matrix/proof003.html
15. Lin, Minghua; Sra, Suvrit (2014). "Superaditividad completamente fuerte de funciones matriciales generalizadas". arXiv : 1410.1958 [math.FA].
16. Paksoy; Turkmen; Zhang (2014). "Desigualdades de funciones matriciales generalizadas mediante productos tensoriales". Revista electrónica de álgebra lineal . 27 : 332–341. doi : 10.13001/1081-3810.1622 .
17. Serre, Denis (18 de octubre de 2010). "Concavidad de det1/n sobre HPDn". MathOverflow .
18. Lang 1985, §VIII.2, Horn y Johnson 2018, Def. 1.2.3
19. Horn & Johnson 2018, Observación 7.1.2, Teorema 7.2.5
20. Se puede encontrar una prueba en el Apéndice B de Kondratyuk, LA; Krivoruchenko, MI (1992). "Materia de quarks superconductores en el grupo de colores SU (2)". Zeitschrift für Physik A. 344 (1): 99-115. Código Bib : 1992ZPhyA.344...99K. doi :10.1007/BF01291027. S2CID  120467300.
21. Horn y Johnson 2018, § 0.8.10
22. Grattan-Guinness 2003, §6.6
23. Cajori, F. Una historia de las matemáticas p. 80
24. Campbell, H: "Álgebra lineal con aplicaciones", páginas 111-112. Appleton Century Crofts, 1971
25. Eves 1990, pág. 405
26. Breve historia del álgebra lineal y la teoría de matrices en: "Breve historia del álgebra lineal y la teoría de matrices". Archivado desde el original el 10 de septiembre de 2012 . Consultado el 24 de enero de 2012 .
27. Kleiner 2007, pág. 80
28. Bourbaki (1994, pág. 59)
29. Muir, Sir Thomas, La teoría de los determinantes en el orden histórico del desarrollo [Londres, Inglaterra: Macmillan and Co., Ltd., 1906]. JFM  37.0181.02
30. Kleiner 2007, §5.2
31. El primer uso de la palabra "determinante" en el sentido moderno apareció en: Cauchy, Augustin-Louis "Memoire sur les fonctions qui ne peuvent obtenir que deux valeurs égales et des signes contraires par suite des transpositions operées entre les variables qu'elles renferment", que fue leído por primera vez en el Instituto de Francia en París el 30 de noviembre de 1812, y que posteriormente fue publicado en el Journal de l'Ecole Polytechnique , Cahier 17, Tomo 10, páginas 29-112 (1815).
32. Orígenes de los términos matemáticos: http://jeff560.tripod.com/d.html
33. Historia de matrices y determinantes: http://www-history.mcs.st-and.ac.uk/history/HistTopics/Matrices_and_determinants.html
34. Eves 1990, pág. 494
35. Cajori 1993, vol. II, pág. 92, núm. 462
36. Historia de la notación matricial: http://jeff560.tripod.com/matrices.html
37. Habgood y Arel 2012
38. Lang 1985, §VII.3
39. Lang 2002, §IV.8
40. Lang 1985, §VII.6, Teorema 6.10
41. Lay, David (2021). Álgebra lineal y sus aplicaciones, sexta edición . Pearson. pág. 172.
42. Dummit y Foote 2004, §11.4
43. Dummit y Foote 2004, §11.4, Teorema 30
44. Mac Lane 1998, §I.4. Véase también Transformación natural § Determinante .
45. Bourbaki 1998, §III.8
46. Lombardi y Quitté 2015, §5.2, Bourbaki 1998, §III.5
47. Garibaldi 2004
48. En un contexto no conmutativo, la linealidad izquierda (compatibilidad con la multiplicación izquierda por escalares) debe distinguirse de la linealidad derecha. Suponiendo que la linealidad en las columnas se toma como linealidad izquierda, se tendría, para escalares no conmutativos a , b : una contradicción. No hay una noción útil de funciones multilineales sobre un anillo no conmutativo. $${\displaystyle {\begin{aligned}ab&=ab{\begin{vmatrix}1&0\\0&1\end{vmatrix}}=a{\begin{vmatrix}1&0\\0&b\end{vmatrix}}\\[5mu]&={\begin{vmatrix}a&0\\0&b\end{vmatrix}}=b{\begin{vmatrix}a&0\\0&1\end{vmatrix}}=ba{\begin{vmatrix}1&0\\0&1\end{vmatrix}}=ba,\end{aligned}}}$$
49. Varadarajan, V. S (2004), Supersimetría para matemáticos: una introducción, American Mathematical Soc., ISBN 978-0-8218-3574-6.
50. "... mencionamos que el determinante, aunque es una noción conveniente teóricamente, rara vez encuentra un papel útil en los algoritmos numéricos.", ver Trefethen & Bau III 1997, Conferencia 1.
51. Fisikopoulos y Peñaranda 2016, §1.1, §4.3
52. Camarero, Cristóbal (5 de diciembre de 2018). "Algoritmos simples, rápidos y practicables para la descomposición de Cholesky, LU y QR utilizando multiplicación rápida de matrices rectangulares". arXiv : 1812.02056 [cs.NA].
53. Bunch y Hopcroft 1974
54. Fisikopoulos y Peñaranda 2016, §1.1
55. Rote 2001
56. Fang, Xin Gui; Havas, George (1997). "Sobre la complejidad en el peor de los casos de la eliminación gaussiana de enteros" (PDF) . Actas del simposio internacional de 1997 sobre computación simbólica y algebraica . ISSAC '97. Kihei, Maui, Hawái, Estados Unidos: ACM. págs. 28–31. doi :10.1145/258726.258740. ISBN . 0-89791-875-4Archivado desde el original (PDF) el 7 de agosto de 2011. Consultado el 22 de enero de 2011 .
57. Fisikopoulos y Peñaranda 2016, §1.1, Bareiss 1968
58. Abeles, Francine F. (2008). "Condensación de Dodgson: El desarrollo histórico y matemático de un método experimental". Álgebra lineal y sus aplicaciones . 429 (2–3): 429–438. doi : 10.1016/j.laa.2007.11.022 .

Referencias

• Anton, Howard (2005), Álgebra lineal elemental (versión de aplicaciones) (novena edición), Wiley International
• Axler, Sheldon Jay (2015). Álgebra lineal bien hecha (3.ª ed.). Springer . ISBN 978-3-319-11079-0.
• Bareiss, Erwin (1968), "Identidad de Sylvester y eliminación gaussiana que preserva números enteros en varios pasos" (PDF) , Mathematics of Computation , 22 (102): 565–578, doi :10.2307/2004533, JSTOR  2004533, archivado (PDF) desde el original el 25 de octubre de 2012
• de Boor, Carl (1990), "Un ejercicio vacío" (PDF) , ACM SIGNUM Newsletter , 25 (2): 3–7, doi :10.1145/122272.122273, S2CID  62780452, archivado (PDF) desde el original el 2006-09-01
• Bourbaki, Nicolas (1998), Álgebra I, Capítulos 1-3 , Springer, ISBN 9783540642435
• Bunch, JR; Hopcroft, JE (1974). "Factorización triangular e inversión mediante multiplicación rápida de matrices". Matemáticas de la computación . 28 (125): 231–236. doi : 10.1090/S0025-5718-1974-0331751-8 . hdl : 1813/6003 .
• Dummit, David S.; Foote, Richard M. (2004), Álgebra abstracta (3.ª ed.), Hoboken, Nueva Jersey: Wiley, ISBN 9780471452348, OCLC  248917264
• Fisikopoulos, Vissarion; Peñaranda, Luis (2016), "Algoritmos geométricos más rápidos mediante el cálculo de determinantes dinámicos", Computational Geometry , 54 : 1–16, arXiv : 1206.7067 , doi : 10.1016/j.comgeo.2015.12.001
• Garibaldi, Skip (2004), "El polinomio característico y el determinante no son construcciones ad hoc", American Mathematical Monthly , 111 (9): 761–778, arXiv : math/0203276 , doi :10.2307/4145188, JSTOR  4145188, MR  2104048
• Habgood, Ken; Arel, Itamar (2012). "Una aplicación basada en condensación de la regla de Cramer para resolver sistemas lineales a gran escala" (PDF) . Journal of Discrete Algorithms . 10 : 98–109. doi : 10.1016/j.jda.2011.06.007 . Archivado (PDF) desde el original el 2019-05-05.
• Harris, Frank E. (2014), Matemáticas para la ciencia física y la ingeniería , Elsevier, ISBN 9780128010495
• Kleiner, Israel (2007), Kleiner, Israel (ed.), Una historia del álgebra abstracta , Birkhäuser, doi :10.1007/978-0-8176-4685-1, ISBN 978-0-8176-4684-4, Sr.  2347309
• Kung, Joseph PS; Rota, Gian-Carlo; Yan, Catherine (2009), Combinatoria: The Rota Way , Cambridge University Press, ISBN 9780521883894
• Lay, David C. (22 de agosto de 2005), Álgebra lineal y sus aplicaciones (3.ª ed.), Addison Wesley, ISBN 978-0-321-28713-7
• Lombardi, Enrique; Quitté, Claude (2015), Álgebra conmutativa: métodos constructivos , Springer, ISBN 9789401799447
• Mac Lane, Saunders (1998), Categorías para el matemático en activo , Textos de posgrado en matemáticas 5 (2.ª ed.), Springer-Verlag, ISBN 0-387-98403-8
• Meyer, Carl D. (15 de febrero de 2001), Análisis matricial y álgebra lineal aplicada, Sociedad de Matemáticas Industriales y Aplicadas (SIAM), ISBN 978-0-89871-454-8, archivado desde el original el 31 de octubre de 2009
• Muir, Thomas (1960) [1933], Un tratado sobre la teoría de los determinantes , revisado y ampliado por William H. Metzler, Nueva York, NY: Dover
• Poole, David (2006), Álgebra lineal: una introducción moderna (2.ª ed.), Brooks/Cole, ISBN 0-534-99845-3
• G. Baley Price (1947) "Algunas identidades en la teoría de determinantes", American Mathematical Monthly 54:75–90 MR 0019078
• Horn, Roger Alan ; Johnson, Charles Royal (2018) [1985]. Análisis de matrices (2.ª ed.). Cambridge University Press . ISBN 978-0-521-54823-6.
• Lang, Serge (1985), Introducción al álgebra lineal , Textos de pregrado en matemáticas (2.ª ed.), Springer, ISBN 9780387962054
• Lang, Serge (1987), Álgebra lineal , Textos de pregrado en matemáticas (3.ª ed.), Springer, ISBN 9780387964126
• Lang, Serge (2002). Álgebra . Textos de posgrado en matemáticas. Nueva York, NY: Springer. ISBN 978-0-387-95385-4.
• Leon, Steven J. (2006), Álgebra lineal con aplicaciones (7.ª ed.), Pearson Prentice Hall
• Rote, Günter (2001), "Algoritmos sin división para el determinante y el pfaffiano: enfoques algebraicos y combinatorios" (PDF) , Computational discrete mathematics , Lecture Notes in Comput. Sci., vol. 2122, Springer, pp. 119–135, doi : 10.1007/3-540-45506-X_9 , ISBN 978-3-540-42775-9, MR  1911585, archivado desde el original (PDF) el 2007-02-01 , consultado el 2020-06-04
• Trefethen, Lloyd; Bau III, David (1997), Álgebra lineal numérica (1.ª ed.), Filadelfia: SIAM, ISBN 978-0-89871-361-9

Referencias históricas

• Bourbaki, Nicolas (1994), Elementos de la historia de las matemáticas , traducido por Meldrum, John , Springer, doi :10.1007/978-3-642-61693-8, ISBN 3-540-19376-6
• Cajori, Florian (1993), Una historia de las notaciones matemáticas: Incluyendo el vol. I. Notaciones en matemáticas elementales; vol. II. Notaciones principalmente en matemáticas superiores, Reimpresión de los originales de 1928 y 1929 , Dover, ISBN 0-486-67766-4, Sr.  3363427
• Bézout, Étienne (1779), Théorie générale des ecuaciones algébriques, París
• Cayley, Arthur (1841), "Sobre un teorema en la geometría de la posición", Cambridge Mathematical Journal , 2 : 267–271
• Cramer, Gabriel (1750), Introducción al análisis de las líneas courbes algébriques , Ginebra: Frères Cramer & Cl. Philibert, doi :10.3931/e-rara-4048
• Eves, Howard (1990), Una introducción a la historia de las matemáticas (6.ª ed.), Saunders College Publishing, ISBN 0-03-029558-0, Sr.  1104435
• Grattan-Guinness, I., ed. (2003), Companion Encyclopedia of the History and Philosophy of the Mathematical Sciences , vol. 1, Johns Hopkins University Press , ISBN 9780801873966
• Jacobi, Carl Gustav Jakob (1841), "De Determinantibus funcionalibus", Journal für die reine und angewandte Mathematik , 1841 (22): 320–359, doi :10.1515/crll.1841.22.319, S2CID  123637858
• Laplace, Pierre-Simon, de (1772), "Recherches sur le calcul intégral et sur le systéme du monde", Histoire de l'Académie Royale des Sciences (segunda parte), París: 267–376{{citation}}: CS1 maint: multiple names: authors list (link)

Enlaces externos

• Suprunenko, DA (2001) [1994], "Determinante", Enciclopedia de Matemáticas , EMS Press
• Weisstein, Eric W. "Determinante". MundoMatemático .
• O'Connor, John J.; Robertson, Edmund F. , "Matrices y determinantes", Archivo de Historia de las Matemáticas de MacTutor , Universidad de St Andrews
• Programa interactivo y tutorial sobre determinantes
• Álgebra lineal: determinantes. Archivado el 4 de diciembre de 2008 en Wayback Machine. Calcule los determinantes de matrices de hasta orden 6 utilizando la expansión de Laplace que elija.
• Calculadora de determinantes Calculadora para determinantes matriciales, hasta el octavo orden.
• Matrices y álgebra lineal en los primeros usos Páginas
• Los determinantes se explican de manera sencilla en el capítulo 4 como parte de un curso de Álgebra lineal.