Problema del horizonte

Problema de ajuste fino cosmológico

Si observamos el CMB, se trata de una distancia de 46.000 millones de años luz . Sin embargo, cuando se emitió la luz, el universo era mucho más joven (300.000 años). En ese momento, la luz solo habría llegado hasta los círculos más pequeños. Los dos puntos indicados en el diagrama no habrían podido contactarse entre sí porque sus esferas de causalidad no se superponen.

El problema del horizonte (también conocido como problema de homogeneidad ) es un problema cosmológico de ajuste fino dentro del modelo del Big Bang del universo . Surge debido a la dificultad de explicar la homogeneidad observada de regiones causalmente desconectadas del espacio en ausencia de un mecanismo que establezca las mismas condiciones iniciales en todas partes. Fue señalado por primera vez por Wolfgang Rindler en 1956. ^[1]

La solución más aceptada es la inflación cósmica . Diferentes soluciones proponen un universo cíclico o una velocidad de la luz variable .

Fondo

Distancias astronómicas y horizontes de partículas

Las distancias de los objetos observables en el cielo nocturno corresponden a tiempos del pasado. Usamos el año luz (la distancia que la luz puede viajar en el tiempo de un año terrestre) para describir estas distancias cosmológicas. Una galaxia medida a diez mil millones de años luz nos parece como era hace diez mil millones de años, porque la luz ha tardado ese tiempo en viajar hasta el observador. Si uno mirara una galaxia a diez mil millones de años luz de distancia en una dirección y otra en la dirección opuesta, la distancia total entre ellas es de veinte mil millones de años luz. Esto significa que la luz de la primera aún no ha llegado a la segunda porque el universo tiene solo unos 13.800 millones de años. En un sentido más general, hay porciones del universo que son visibles para nosotros, pero invisibles entre sí, fuera de los respectivos horizontes de partículas de cada una .

Propagación de información causal

En las teorías físicas relativistas aceptadas, ninguna información puede viajar más rápido que la velocidad de la luz . En este contexto, "información" significa "cualquier tipo de interacción física". Por ejemplo, el calor fluirá naturalmente de una zona más caliente a una más fría y, en términos de física, este es un ejemplo de intercambio de información. Dado el ejemplo anterior, las dos galaxias en cuestión no pueden haber compartido ningún tipo de información; no están en contacto causal . En ausencia de condiciones iniciales comunes, cabría esperar, entonces, que sus propiedades físicas fueran diferentes y, de manera más general, que el universo en su conjunto tuviera propiedades variables en regiones causalmente desconectadas.

Problema del horizonte

Contrariamente a esta expectativa, las observaciones del fondo cósmico de microondas (CMB) y los estudios de galaxias muestran que el universo observable es casi isótropo , lo que, a través del principio copernicano , también implica homogeneidad . ^[2] Los estudios del cielo del CMB muestran que las temperaturas del CMB están coordinadas a un nivel de donde es la diferencia entre la temperatura observada en una región del cielo y la temperatura promedio del cielo . Esta coordinación implica que todo el cielo, y por lo tanto todo el universo observable , deben haber estado conectados causalmente el tiempo suficiente para que el universo llegue al equilibrio térmico. ${\displaystyle \Delta T/T\approx 10^{-5},}$ ${\displaystyle \Delta T}$ ${\displaystyle T}$

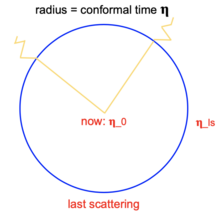
Según el modelo del Big Bang, a medida que la densidad del universo en expansión disminuía, finalmente alcanzó una temperatura en la que los fotones perdieron el equilibrio térmico con la materia; se desacoplaron del plasma de electrones y protones y comenzaron a fluir libremente a través del universo. Este momento en el tiempo se conoce como la época de la recombinación , cuando los electrones y los protones se unieron para formar hidrógeno eléctricamente neutro; sin electrones libres para dispersar los fotones, los fotones comenzaron a fluir libremente. Esta época se observa a través del CMB. Dado que observamos el CMB como un fondo para los objetos a un corrimiento al rojo menor, describimos esta época como la transición del universo de opaco a transparente. El CMB describe físicamente la "superficie de la última dispersión" tal como se nos aparece como una superficie o un fondo, como se muestra en la figura siguiente.

Tenga en cuenta que en los siguientes diagramas utilizamos el tiempo conforme . El tiempo conforme describe el tiempo que le tomaría a un fotón viajar desde la ubicación del observador hasta la distancia observable más lejana (si el universo dejara de expandirse ahora mismo).

El círculo azul es la superficie del CMB que observamos en el momento de la última dispersión. Las líneas amarillas describen cómo se dispersaron los fotones antes de la época de recombinación y cómo se dispersaron libremente después. El observador se encuentra en el centro en el momento actual. Como referencia.

Se cree que el desacoplamiento, o la última dispersión, ocurrió unos 300.000 años después del Big Bang, o con un corrimiento al rojo de aproximadamente . Podemos determinar tanto el diámetro angular aproximado del universo como el tamaño físico del horizonte de partículas que existía en ese momento. ${\displaystyle z_{rec}\approx 1100}$

La distancia del diámetro angular , en términos de corrimiento al rojo , se describe mediante . Si asumimos una cosmología plana , entonces, ${\displaystyle z}$ ${\displaystyle d_{A}(z)=r(z)/(1+z)}$

${\displaystyle r(z)=\int _{t_{em}}^{t_{0}}{\frac {dt}{a(t)}}=\int _{a_{em}}^{1}{\frac {da}{a^{2}H(a)}}=\int _{0}^{z}{\frac {dz}{H(z)}}.}$

La época de recombinación ocurrió durante una era del universo dominada por la materia, por lo que podemos aproximarnos como . Al unirlos, vemos que la distancia del diámetro angular, o el tamaño del universo observable para un corrimiento al rojo es ${\displaystyle H(z)}$ ${\displaystyle H^{2}(z)\approx \Omega _{m}H_{0}^{2}(1+z)^{3}}$ ${\displaystyle z_{rec}\approx 1100}$

${\displaystyle r(z)=\int _{0}^{z}{\frac {dz}{H(z)}}={\frac {1}{{\sqrt {\Omega _{m}}}H_{0}}}\int _{0}^{z}{\frac {dz}{(1+z)^{3/2}}}={\frac {2}{{\sqrt {\Omega _{m}}}H_{0}}}\left(1-{\frac {1}{\sqrt {1+z}}}\right).}$

Dado que , podemos aproximar la ecuación anterior como ${\displaystyle z\gg 1}$

${\displaystyle r(z)\approx {\frac {2}{{\sqrt {\Omega _{m}}}H_{0}}}.}$

Sustituyendo esto en nuestra definición de distancia de diámetro angular, obtenemos

${\displaystyle d_{A}(z)\approx {\frac {2}{{\sqrt {\Omega _{m}}}H_{0}}}{\frac {1}{1+z}}.}$

A partir de esta fórmula, obtenemos la distancia del diámetro angular del fondo cósmico de microondas como . ${\displaystyle d_{A}(1100)\approx 14\ \mathrm {Mpc} }$

El horizonte de partículas describe la distancia máxima que las partículas de luz podrían haber recorrido hasta el observador dada la edad del universo. Podemos determinar la distancia de co-movimiento para la edad del universo en el momento de la recombinación utilizando datos anteriores, ${\displaystyle r(z)}$

${\displaystyle d_{\text{hor,rec}}(z)=\int _{0}^{t(z)}{\frac {dt}{a(t)}}=\int _{z}^{\infty }{\frac {dz}{H(z)}}\approx {\frac {2}{{\sqrt {\Omega _{m}}}H_{0}}}\left[{\frac {1}{\sqrt {1+z}}}\right]_{z}^{\infty }\approx {\frac {2}{{\sqrt {\Omega _{m}}}H_{0}}}{\frac {1}{\sqrt {1+z}}}}$

Este diagrama de espacio-tiempo muestra cómo los conos de luz de dos partículas de luz separadas a cierta distancia en el momento de la última dispersión (ls) no se intersecan (es decir, están desconectados causalmente). El eje horizontal es la distancia comóvil, el eje vertical es el tiempo conforme y las unidades tienen la velocidad de la luz como 1. Para referencia.

Para obtener el tamaño físico del horizonte de partículas , ${\displaystyle D}$

${\displaystyle D(z)=a(z)d_{\text{hor,rec}}={\frac {d_{\text{hor,rec}}(z)}{1+z}}}$

${\displaystyle D(1100)\approx 0.03~{\text{radians}}\approx 2^{\circ }}$

Cabría esperar que cualquier región del CMB dentro de los 2 grados de separación angular hubiera estado en contacto causal, pero a cualquier escala mayor a 2° no debería haber habido intercambio de información.

Las regiones del CMB que están separadas por más de 2° se encuentran fuera de los horizontes de partículas de cada una y están desconectadas causalmente. El problema del horizonte describe el hecho de que vemos isotropía en la temperatura del CMB en todo el cielo, a pesar de que todo el cielo no está en contacto causal para establecer el equilibrio térmico. Consulte el diagrama de tiempo-espacio a la derecha para ver una visualización de este problema.

Si el universo comenzó con temperaturas levemente diferentes en distintos lugares, el CMB no debería ser isótropo a menos que exista un mecanismo que equilibre la temperatura en el momento del desacoplamiento. En realidad, el CMB tiene la misma temperatura en todo el cielo, 2,726 ± 0,001 K. [ ^3]

Modelo inflacionario

Este diagrama de espacio-tiempo muestra cómo la inflación cambia los conos de luz de dos partículas de luz que se encuentran a cierta distancia en el momento de la última dispersión (ls) para permitir que se crucen. En este escenario, están en contacto causal y pueden intercambiar información entre sí. El eje horizontal es la distancia comóvil, el eje vertical es el tiempo conforme y las unidades tienen la velocidad de la luz como 1. Para referencia.

La teoría de la inflación cósmica ha intentado abordar el problema postulando un período de 10 ⁻³² segundos de expansión exponencial en el primer segundo de la historia del universo debido a una interacción de campo escalar. ^[4] Según el modelo inflacionario, el universo aumentó de tamaño en un factor de más de 10 ²² , desde una región pequeña y causalmente conectada en casi equilibrio. ^[5] La inflación luego expandió el universo rápidamente, aislando regiones cercanas del espacio-tiempo al hacerlas crecer más allá de los límites del contacto causal, "bloqueando" efectivamente la uniformidad a grandes distancias. Esencialmente, el modelo inflacionario sugiere que el universo estaba completamente en contacto causal en el universo muy temprano. La inflación luego expande este universo en aproximadamente 60 e-plegados (el factor de escala aumenta en el factor ). Observamos el CMB después de que la inflación haya ocurrido a una escala muy grande. Mantuvo el equilibrio térmico a este gran tamaño debido a la rápida expansión de la inflación. ${\displaystyle e^{60}}$

Una consecuencia de la inflación cósmica es que las anisotropías en el Big Bang debidas a fluctuaciones cuánticas se reducen pero no se eliminan. Las diferencias en la temperatura del fondo cósmico se suavizan por la inflación cósmica, pero siguen existiendo. La teoría predice un espectro para las anisotropías en el fondo de microondas que es en gran parte consistente con las observaciones de WMAP y COBE . ^[6]

Sin embargo, la gravedad por sí sola puede ser suficiente para explicar esta homogeneidad. ^[7]

Teorías de velocidad variable de la luz

Se han propuesto modelos cosmológicos que emplean una velocidad variable de la luz para resolver el problema del horizonte de la inflación cósmica y proporcionar una alternativa a la misma . En los modelos VSL, la constante fundamental c , que denota la velocidad de la luz en el vacío, es mayor en el universo temprano que su valor actual, lo que aumenta efectivamente el horizonte de partículas en el momento del desacoplamiento lo suficiente como para explicar la isotropía observada del CMB.

Véase también

• Problema de planitud
• Monopolo magnético

Referencias

1. Carrigan, Richard A.; Trower, W. Peter (1983). Monopolos magnéticos . doi :10.1007/978-1-4615-7370-8. ISBN 978-1-4615-7372-2.
2. "Física Cosmológica".
3. Fixsen, DJ (2009). "La temperatura del fondo cósmico de microondas". The Astrophysical Journal . 707 (2): 916–920. arXiv : 0911.1955 . Código Bibliográfico :2009ApJ...707..916F. doi :10.1088/0004-637X/707/2/916. S2CID  119217397.
4. Una exposición sobre la cosmología inflacionaria, Gary Scott Watson, Departamento de Física, Universidad de Brown
5. Remmen, Grant N.; Carroll, Sean M. (2014). "¿Cuántos e-folds deberíamos esperar de la inflación a gran escala?". Physical Review D . 90 (6): 063517. arXiv : 1405.5538 . Bibcode :2014PhRvD..90f3517R. doi :10.1103/PhysRevD.90.063517. ISSN  1550-7998. S2CID  37669055.
6. Starkman, Glenn D. y Dominic J. Schwarz; Scientific American (se requiere suscripción)
7. Fajman, David (22 de septiembre de 2020). "La gravedad provoca la homogeneidad del universo".

Enlaces externos

• Diferentes horizontes en la cosmología