En matemáticas , el número de Strahler o número de Horton-Strahler de un árbol matemático es una medida numérica de su complejidad de ramificación.
Estos números fueron desarrollados por primera vez en hidrología , como una forma de medir la complejidad de los ríos y arroyos, por Robert E. Horton (1945) y Arthur Newell Strahler (1952, 1957). En esta aplicación, se los conoce como el orden de corrientes de Strahler y se utilizan para definir el tamaño de las corrientes en función de una jerarquía de afluentes . Los mismos números también surgen en el análisis de sistemas L y de estructuras biológicas jerárquicas como árboles (biológicos) y sistemas respiratorios y circulatorios animales, en la asignación de registros para la compilación de lenguajes de programación de alto nivel y en el análisis de redes sociales .
Todos los árboles en este contexto son grafos dirigidos , orientados desde la raíz hacia las hojas; en otras palabras, son arborescencias . El grado de un nodo en un árbol es simplemente su número de hijos. Se puede asignar un número de Strahler a todos los nodos de un árbol, en orden ascendente, de la siguiente manera:
El número de Strahler de un árbol es el número de su nodo raíz.
Algorítmicamente , estos números pueden asignarse realizando una búsqueda en profundidad y asignando el número de cada nodo en postorder . Los mismos números también pueden generarse mediante un proceso de poda en el que el árbol se simplifica en una secuencia de etapas, donde en cada etapa se eliminan todos los nodos de hoja y todos los caminos de los nodos de grado uno que conducen a las hojas: el número de Strahler de un nodo es la etapa en la que se eliminaría mediante este proceso, y el número de Strahler de un árbol es el número de etapas necesarias para eliminar todos sus nodos. Otra definición equivalente del número de Strahler de un árbol es que es la altura del árbol binario completo más grande que se puede incrustar homeomórficamente en el árbol dado; el número de Strahler de un nodo en un árbol es de manera similar la altura del árbol binario completo más grande que se puede incrustar debajo de ese nodo.
Cualquier nodo con número de Strahler i debe tener al menos dos descendientes con número de Strahler i − 1, al menos cuatro descendientes con número de Strahler i − 2, etc., y al menos 2 i − 1 descendientes de hojas. Por lo tanto, en un árbol con n nodos, el mayor número de Strahler posible es log 2 n + 1. [1] Sin embargo, a menos que el árbol forme un árbol binario completo, su número de Strahler será menor que este límite. En un árbol binario de n nodos , elegido de manera uniforme al azar entre todos los árboles binarios posibles , el índice esperado de la raíz es con alta probabilidad muy cercano a log 4 n . [2]
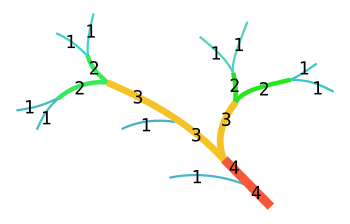
En la aplicación del orden de corrientes de Strahler a la hidrología, cada segmento de una corriente o río dentro de una red fluvial se trata como un nodo en un árbol, con el siguiente segmento aguas abajo como su padre. Cuando dos corrientes de primer orden se unen, forman una corriente de segundo orden . Cuando dos corrientes de segundo orden se unen, forman una corriente de tercer orden . Las corrientes de orden inferior que se unen a una corriente de orden superior no cambian el orden de la corriente superior. Por lo tanto, si una corriente de primer orden se une a una corriente de segundo orden, sigue siendo una corriente de segundo orden. No es hasta que una corriente de segundo orden se combina con otra corriente de segundo orden que se convierte en una corriente de tercer orden. Al igual que con los árboles matemáticos, un segmento con índice i debe ser alimentado por al menos 2 i − 1 afluentes diferentes de índice 1. Shreve señaló que las Leyes de Horton y Strahler deberían esperarse de cualquier distribución topológicamente aleatoria. Una revisión posterior de las relaciones confirmó este argumento, estableciendo que, a partir de las propiedades que describen las leyes, no se puede extraer ninguna conclusión para explicar la estructura o el origen de la red de corrientes. [3] [4]
Para que una característica hidrológica se considere corriente, debe ser recurrente o perenne . Las corrientes recurrentes (o "intermitentes") tienen agua en el cauce durante al menos una parte del año. El índice de una corriente o río puede variar de 1 (una corriente sin afluentes) a 12 (el río más caudaloso del mundo, el Amazonas , en su desembocadura). El río Ohio es de orden ocho y el río Misisipi de orden 10. Se estima que el 80% de las corrientes del planeta son corrientes de cabecera de primer a tercer orden . [5]
Si la relación de bifurcación de una red fluvial es alta, entonces hay una mayor probabilidad de inundaciones. También habría un menor tiempo de concentración. [6] La relación de bifurcación también puede mostrar qué partes de una cuenca de drenaje tienen más probabilidades de inundarse, comparativamente, al observar las relaciones por separado. La mayoría de los ríos británicos tienen una relación de bifurcación de entre 3 y 5. [7]
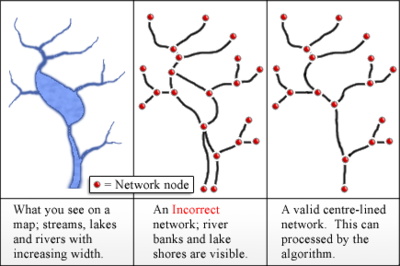
Gleyzer et al. (2004) describen cómo calcular los valores de ordenamiento de corrientes de Strahler en una aplicación SIG . Este algoritmo está implementado por RivEX, una herramienta ESRI ArcGIS Pro 3.3.x. La entrada de su algoritmo es una red de líneas centrales de los cuerpos de agua, representadas como arcos (o bordes) unidos en nodos. Los límites de lagos y las riberas de los ríos no deben usarse como arcos, ya que generalmente formarán una red no arbórea con una topología incorrecta.
Shreve [8] [9] y Hodgkinson et al. [3] han desarrollado sistemas alternativos de ordenación de corrientes. Smart [10] ofrece una comparación estadística de los sistemas de Strahler y Shreve, junto con un análisis de las longitudes de corrientes/enlaces.
La numeración de Strahler se puede aplicar en el análisis estadístico de cualquier sistema jerárquico, no sólo de ríos.
Al traducir un lenguaje de programación de alto nivel a lenguaje ensamblador, el número mínimo de registros necesarios para evaluar un árbol de expresiones es exactamente su número de Strahler. En este contexto, el número de Strahler también puede denominarse número de registro . [13]
Para los árboles de expresión que requieren más registros de los que están disponibles, se puede utilizar el algoritmo Sethi-Ullman para traducir un árbol de expresión en una secuencia de instrucciones de máquina que utiliza los registros de la manera más eficiente posible, minimizando la cantidad de veces que los valores intermedios se transfieren de los registros a la memoria principal y la cantidad total de instrucciones en el código compilado resultante.
Asociados con los números de Strahler de un árbol están los índices de bifurcación , números que describen qué tan cerca está un árbol del equilibrio. Para cada orden i en una jerarquía, el i- ésimo índice de bifurcación es
donde n i denota el número de nodos con orden i .
La razón de bifurcación de una jerarquía general se puede obtener promediando las razones de bifurcación en diferentes órdenes. En un árbol binario completo, la razón de bifurcación será 2, mientras que otros árboles tendrán razones de bifurcación mayores. Es un número adimensional.
El ancho de camino de un grafo arbitrario no dirigido G puede definirse como el número más pequeño w tal que existe un grafo de intervalo H que contiene a G como subgrafo, con la camarilla más grande en H que tiene w + 1 vértices. Para los árboles (vistos como grafos no dirigidos al olvidar su orientación y raíz) el ancho de camino difiere del número de Strahler, pero está estrechamente relacionado con él: en un árbol con ancho de camino w y número de Strahler s , estos dos números están relacionados por las desigualdades [14]
La capacidad de manejar gráficos con ciclos y no solo árboles le otorga a pathwidth una versatilidad adicional en comparación con el número de Strahler. Sin embargo, a diferencia del número de Strahler, el pathwidth se define solo para todo el gráfico y no por separado para cada nodo del gráfico.