La difracción de fibra es una subárea de la dispersión , un área en la que la estructura molecular se determina a partir de datos de dispersión (generalmente de rayos X, electrones o neutrones). En la difracción de fibra, el patrón de dispersión no cambia, ya que la muestra gira alrededor de un eje único (el eje de la fibra). Tal simetría uniaxial es frecuente con filamentos o fibras que consisten en macromoléculas biológicas o artificiales . En cristalografía , la simetría de fibra es una complicación con respecto a la determinación de la estructura cristalina, porque las reflexiones se difuminan y pueden superponerse en el patrón de difracción de fibra. La ciencia de los materiales considera la simetría de fibra como una simplificación, porque casi la información de estructura obtenible completa está en un solo patrón de difracción bidimensional (2D) expuesto en una película fotográfica o en un detector 2D. 2 en lugar de 3 direcciones de coordenadas son suficientes para describir la difracción de fibra.
El patrón ideal de fibra exhibe simetría de 4 cuadrantes . En el patrón ideal, el eje de la fibra se llama meridiano , la dirección perpendicular se llama ecuador . En caso de simetría de fibra, aparecen en el patrón 2D muchas más reflexiones que en la difracción de monocristal. En los patrones de fibra, estas reflexiones aparecen claramente dispuestas a lo largo de líneas ( líneas de capa ) que corren casi paralelas al ecuador. Por lo tanto, en la difracción de fibra, el concepto de línea de capa de la cristalografía se vuelve palpable. Las líneas de capa dobladas indican que el patrón debe enderezarse. Las reflexiones se etiquetan con el índice de Miller hkl, es decir, 3 dígitos. Las reflexiones en la i -ésima línea de capa comparten l = i . Las reflexiones en el meridiano son reflexiones 00l. En cristalografía, los patrones de difracción de fibra artificiales se generan rotando un monocristal alrededor de un eje ( método de cristal giratorio ).
En los experimentos se obtienen patrones de fibra no ideales. Sólo muestran simetría especular respecto del meridiano. La razón es que el eje de la fibra y el haz incidente (rayos X, electrones, neutrones) no pueden estar perfectamente orientados perpendicularmente entre sí. La distorsión geométrica correspondiente ha sido estudiada extensamente por Michael Polanyi introduciendo el concepto de esfera de Polanyi (en alemán: "Lagenkugel") que intersecta la esfera de Ewald . Más tarde, Rosalind Franklin y Raymond Gosling han llevado a cabo su propio razonamiento geométrico y han presentado una ecuación aproximada para el ángulo de inclinación de la fibra β. El análisis comienza mapeando el patrón 2D distorsionado en el plano representativo de la fibra. Este es el plano que contiene el eje del cilindro en el espacio recíproco . En cristalografía, primero se calcula una aproximación del mapeo en el espacio recíproco que se refina iterativamente. El método digital, frecuentemente llamado corrección de Fraser, comienza a partir de la aproximación de Franklin para el ángulo de inclinación β. Elimina la inclinación de la fibra, deforma la imagen del detector y corrige la intensidad de dispersión. Norbert Stribeck ha presentado la ecuación correcta para la determinación de β.
Los materiales fibrosos como la lana o el algodón forman fácilmente haces alineados y estuvieron entre las primeras macromoléculas biológicas estudiadas por difracción de rayos X, en particular por William Astbury a principios de la década de 1930. Los datos de difracción de fibras condujeron a varios avances importantes en el desarrollo de la biología estructural , por ejemplo, los modelos originales de la hélice α y el modelo Watson-Crick del ADN bicatenario .
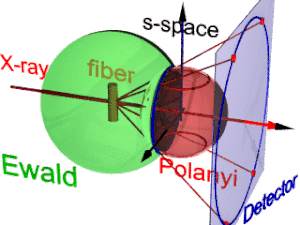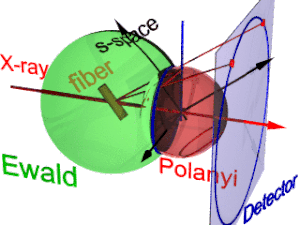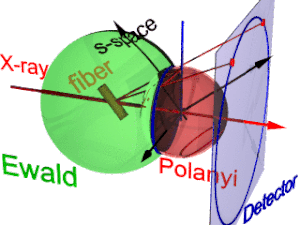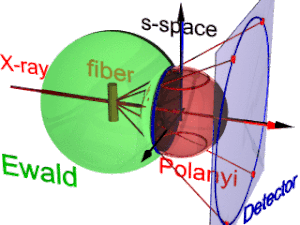
La animación muestra la geometría de la difracción de fibras. Se basa en las nociones propuestas por Michael Polanyi . La dirección de referencia es el haz primario (etiqueta: rayos X). Si la fibra se inclina con respecto a la dirección perpendicular en un ángulo β, también se inclina la información sobre su estructura molecular en el espacio recíproco (triedro etiquetado como espacio s ). En el espacio recíproco, la esfera de Ewald tiene su centro en la muestra. Su radio es 1/λ, donde λ es la longitud de onda de la radiación incidente. En la superficie de la esfera de Ewald se encuentran todos los puntos del espacio recíproco que ve el detector. Estos puntos se mapean en los píxeles del detector mediante proyección central.
En el espacio s, cada reflexión se encuentra en su esfera de Polanyi. Intrínsecamente, la reflexión ideal es un punto en el espacio s, pero la simetría de la fibra la convierte en un anillo que se extiende por la rotación alrededor de la dirección de la fibra. Dos anillos representan cada reflexión en la esfera de Polanyi, porque la dispersión es simétrica con respecto al origen del espacio s. En el detector se representan únicamente los puntos de la reflexión en el espacio s que están tanto en la esfera de Ewald como en la esfera de Polanyi. Estos puntos forman el círculo de reflexión (anillo azul). No cambia cuando se inclina la fibra. Al igual que con un proyector de diapositivas, el círculo de reflexión se proyecta (rayos rojos en movimiento) en el detector ( círculo del detector , anillo azul). Allí pueden aparecer hasta 4 imágenes (puntos rojos) de la reflexión monitoreada. La posición de las imágenes de reflexión es una función de la orientación de la fibra en el haz primario ( ecuación de Polanyi ). Invertida, a partir de las posiciones de las imágenes de reflexión se puede determinar la orientación de la fibra, si para el índice de Miller tanto y es válido. A partir de la representación de Polanyi de la geometría de difracción de la fibra se establecen las relaciones del mapeo de la fibra mediante geometría elemental y esférica.


La figura de la izquierda muestra un patrón típico de fibras de polipropileno antes de su representación en el espacio recíproco. El eje del espejo en el patrón está rotado en un ángulo con respecto a la dirección vertical. Esta deficiencia se compensa con una simple rotación de la imagen. 4 flechas rectas apuntan a 4 imágenes de reflexión de una reflexión de referencia elegida. Sus posiciones se utilizan para determinar el ángulo de inclinación de la fibra . La imagen se ha registrado en un detector CCD. Muestra la intensidad logarítmica en representación pseudocolor. Aquí los colores brillantes representan alta intensidad.
Después de calcular la distancia entre la muestra y el detector utilizando datos cristalográficos conocidos de la reflexión de referencia, se construye un mapa de cuadrícula uniforme para el plano de fibra representativo en el espacio recíproco y se introducen en este mapa los datos de difracción. La figura de la derecha muestra el resultado. En el proceso de desbarbado se ha tenido en cuenta el cambio de intensidad de dispersión. Debido a la curvatura de la superficie de la esfera de Ewald quedan puntos blancos en el meridiano en los que falta información de estructura. Solo en el centro de la imagen y en un valor s relacionado con el ángulo de dispersión hay información de estructura en el meridiano. Por supuesto, ahora hay simetría de 4 cuadrantes. Esto significa que en el patrón de ejemplo parte de la información faltante puede copiarse "de la mitad inferior a la mitad superior" en las áreas blancas. Por lo tanto, a menudo tiene sentido inclinar la fibra intencionadamente.
El esquema tridimensional demuestra que en el experimento de ejemplo la información recopilada sobre la estructura molecular de la fibra de polipropileno está casi completa. Al girar el patrón plano alrededor del meridiano, los datos de dispersión recopilados en 4 s llenan un volumen casi esférico del espacio s. En el ejemplo, todavía no se ha tenido en cuenta la simetría de 4 cuadrantes para rellenar parte de los puntos blancos. Para mayor claridad, se ha recortado un cuarto de la esfera, pero se ha conservado el plano ecuatorial.