
En astronomía , una curva de luz es un gráfico de la intensidad de la luz de un objeto o región celeste en función del tiempo, normalmente con la magnitud de la luz recibida en el eje y y con el tiempo en el eje x . La luz suele estar en un intervalo o banda de frecuencia particular .
Las curvas de luz pueden ser periódicas, como en el caso de las binarias eclipsantes , las variables cefeidas , otras variables periódicas y los planetas extrasolares en tránsito ; o aperiódicas , como la curva de luz de una nova , una estrella variable cataclísmica , una supernova , un fenómeno de microlente o una binaria como la observada durante fenómenos de ocultación . El estudio de la curva de luz, junto con otras observaciones, puede proporcionar información considerable sobre el proceso físico que la produce o limitar las teorías físicas al respecto.
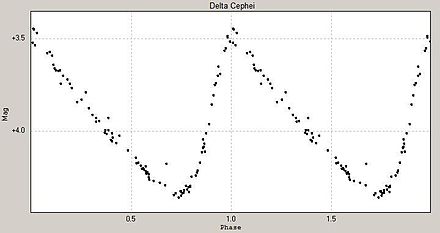
Los gráficos de la magnitud aparente de una estrella variable a lo largo del tiempo se utilizan habitualmente para visualizar y analizar su comportamiento. Aunque la categorización de los tipos de estrellas variables se realiza cada vez más a partir de sus propiedades espectrales, las amplitudes, los períodos y la regularidad de sus cambios de brillo siguen siendo factores importantes. Algunos tipos, como las cefeidas, tienen curvas de luz extremadamente regulares con exactamente el mismo período, amplitud y forma en cada ciclo. Otras, como las variables Mira, tienen curvas de luz algo menos regulares con grandes amplitudes de varias magnitudes, mientras que las variables semirregulares son aún menos regulares y tienen amplitudes más pequeñas. [1]
Las formas de las curvas de luz de las estrellas variables proporcionan información valiosa sobre los procesos físicos subyacentes que producen los cambios de brillo. En el caso de las estrellas variables eclipsantes, la forma de la curva de luz indica el grado de totalidad, los tamaños relativos de las estrellas y sus brillos superficiales relativos. [2] También puede mostrar la excentricidad de la órbita y las distorsiones en la forma de las dos estrellas. [3] En el caso de las estrellas pulsantes, la amplitud o el período de las pulsaciones se pueden relacionar con la luminosidad de la estrella, y la forma de la curva de luz puede ser un indicador del modo de pulsación. [4]

Las curvas de luz de las supernovas pueden ser indicativas del tipo de supernova. Aunque los tipos de supernova se definen en función de sus espectros, cada uno tiene formas de curva de luz típicas. Las supernovas de tipo I tienen curvas de luz con un máximo pronunciado y declinan gradualmente, mientras que las supernovas de tipo II tienen máximos menos pronunciados. Las curvas de luz son útiles para la clasificación de supernovas débiles y para la determinación de subtipos. Por ejemplo, el tipo II-P (para meseta) tiene espectros similares al tipo II-L (lineal) pero se distinguen por una curva de luz donde el declive se aplana durante varias semanas o meses antes de reanudar su declive. [5]
En la ciencia planetaria , una curva de luz se puede utilizar para derivar el período de rotación de un planeta menor , una luna o el núcleo de un cometa . Desde la Tierra a menudo no hay forma de resolver un objeto pequeño en el Sistema Solar , incluso en los telescopios más potentes , ya que el tamaño angular aparente del objeto es menor que un píxel en el detector. Por lo tanto, los astrónomos miden la cantidad de luz producida por un objeto en función del tiempo (la curva de luz). La separación temporal de los picos en la curva de luz proporciona una estimación del período de rotación del objeto. La diferencia entre los brillos máximo y mínimo (la amplitud de la curva de luz) puede deberse a la forma del objeto o a áreas brillantes y oscuras en su superficie. Por ejemplo, la curva de luz de un asteroide asimétrico generalmente tiene picos más pronunciados, mientras que la curva de luz de un objeto más esférico será más plana. [6] Esto permite a los astrónomos inferir información sobre la forma y el giro (pero no el tamaño) de los asteroides.
La base de datos de curvas de luz de asteroides (LCDB) del Collaborative Asteroid Lightcurve Link (CALL) utiliza un código numérico para evaluar la calidad de una solución de período para las curvas de luz de planetas menores (no evalúa necesariamente los datos subyacentes reales). Su parámetro de código de calidad U varía de 0 (incorrecto) a 3 (bien definido): [7]
También se utiliza un signo más (+) o un signo menos (−) al final para indicar una calidad ligeramente mejor o peor que el valor sin signo. [7]

La curva de luz de ocultación suele caracterizarse como binaria, donde la luz de la estrella se detiene instantáneamente, permanece constante durante el tiempo que dura y se restablece instantáneamente. La duración es equivalente a la longitud de una cuerda que atraviesa el cuerpo que oculta.
Las circunstancias en las que las transiciones no son instantáneas son:
Las observaciones generalmente se registran utilizando un equipo de video y la desaparición y reaparición se cronometran utilizando un insertador de tiempo de video (VTI) controlado por GPS .
Las curvas de luz de ocultación están archivadas en el servicio VizieR . [9]
Las caídas periódicas en la curva de luz de una estrella podrían deberse a que un exoplaneta pasa por delante de la estrella que orbita. Cuando un exoplaneta pasa por delante de su estrella, la luz de esa estrella se bloquea temporalmente, lo que da lugar a una caída en la curva de luz de la estrella. Estas caídas son periódicas, ya que los planetas orbitan periódicamente alrededor de una estrella. Se han descubierto muchos exoplanetas mediante este método, que se conoce como el método de tránsito astronómico .
La inversión de la curva de luz es una técnica matemática que se utiliza para modelar las superficies de objetos giratorios a partir de sus variaciones de brillo. Esto se puede utilizar para obtener imágenes efectivas de manchas estelares o albedos de la superficie de asteroides . [10] [11]
La microlente es un proceso en el que objetos astronómicos relativamente pequeños y de baja masa provocan un pequeño y breve aumento en el brillo de un objeto más distante. Esto es causado por el pequeño efecto relativista de las lentes gravitacionales más grandes , pero permite la detección y el análisis de objetos de masa estelar y planetaria que de otro modo serían invisibles. Las propiedades de estos objetos se pueden inferir a partir de la forma de la curva de luz de la lente. Por ejemplo, PA-99-N2 es un evento de microlente que puede haberse debido a una estrella en la galaxia de Andrómeda que tiene un exoplaneta . [12]