El código tórico es un código de corrección de errores cuánticos topológicos y un ejemplo de código estabilizador , definido en una red de espín bidimensional . [1] Es el más simple y mejor estudiado de los modelos cuánticos dobles. [2] También es el ejemplo más simple de orden topológico : orden topológico Z 2 (estudiado por primera vez en el contexto del líquido de espín Z 2 en 1991). [3] [4] El código tórico también puede considerarse una teoría de calibración de red Z 2 en un límite particular. [5] Fue introducido por Alexei Kitaev .
El código tórico recibe su nombre de sus condiciones de contorno periódicas, que le dan la forma de un toro . Estas condiciones le dan al modelo invariancia traslacional, lo que resulta útil para el estudio analítico. Sin embargo, algunas realizaciones experimentales requieren condiciones de contorno abiertas, lo que permite que el sistema se incruste en una superficie 2D. El código resultante se conoce normalmente como código planar. Este tiene un comportamiento idéntico al código tórico en la mayoría de los casos, pero no en todos.
El código tórico se define en una red bidimensional, generalmente elegida como red cuadrada , con un grado de libertad de espín ½ ubicado en cada borde. Se eligen para que sean periódicos. Los operadores estabilizadores se definen en los espines alrededor de cada vértice y plaqueta [ definición necesaria ] (o cara, es decir, un vértice de la red dual) [ aclaración necesaria ] de la red de la siguiente manera:
Donde aquí usamos para denotar los bordes que tocan el vértice y para denotar los bordes que rodean la plaqueta . El espacio estabilizador del código es aquel para el cual todos los estabilizadores actúan trivialmente, por lo tanto, para cualquier estado en este espacio se cumple que
Para el código tórico, este espacio es de cuatro dimensiones, por lo que se puede utilizar para almacenar dos cúbits de información cuántica . Esto se puede demostrar considerando el número de operadores estabilizadores independientes. La aparición de errores moverá el estado fuera del espacio estabilizador, lo que dará como resultado vértices y plaquetas para los que la condición anterior no se cumple. Las posiciones de estas violaciones son el síndrome del código, que se puede utilizar para la corrección de errores.
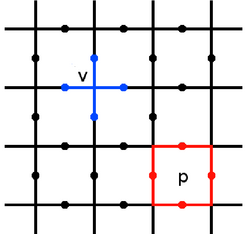
La naturaleza única de los códigos topológicos, como el código tórico, es que las violaciones de los estabilizadores pueden interpretarse como cuasipartículas . En concreto, si el código se encuentra en un estado tal que,
,
Se puede decir que en el vértice existe una cuasipartícula conocida como anión . De manera similar, las violaciones de la están asociadas con los llamados anión en las plaquetas. Por lo tanto, el espacio estabilizador corresponde al vacío aniónico. Los errores de espín individuales hacen que se creen pares de anión y se transporten por la red.
Cuando los errores crean un par de anyones y mueven los anyones, se puede imaginar una ruta que conecta los dos y que está compuesta por todos los enlaces sobre los que se actúa. Si los anyones se encuentran y se aniquilan, esta ruta describe un bucle. Si el bucle es topológicamente trivial, no tiene efecto sobre la información almacenada. La aniquilación de los anyones, en este caso, corrige todos los errores involucrados en su creación y transporte. Sin embargo, si el bucle es topológicamente no trivial, aunque la nueva aniquilación de los anyones devuelve el estado al espacio estabilizador, también implementa una operación lógica sobre la información almacenada. Por lo tanto, en este caso, los errores no se corrigen, sino que se consolidan.
Consideremos el modelo de ruido para el cual los errores de bit y fase ocurren independientemente en cada espín, ambos con probabilidad p . Cuando p es bajo, esto creará pares de anyones escasamente distribuidos que no se han movido mucho de su punto de creación. La corrección se puede lograr identificando los pares en los que se crearon los anyones (hasta una clase de equivalencia) y luego volviéndolos a aniquilar para eliminar los errores. Sin embargo, a medida que p aumenta, se vuelve más ambiguo en cuanto a cómo se pueden emparejar los anyones sin correr el riesgo de la formación de bucles topológicamente no triviales. Esto da una probabilidad umbral, bajo la cual la corrección de error tendrá éxito casi con certeza. A través de un mapeo al modelo de Ising de enlace aleatorio, se ha encontrado que esta probabilidad crítica es de alrededor del 11%. [6]
También se pueden considerar otros modelos de error y encontrar umbrales. En todos los casos estudiados hasta ahora, se ha encontrado que el código satura el límite de Hashing . Para algunos modelos de error, como errores sesgados donde los errores de bit ocurren con más frecuencia que los errores de fase o viceversa, se deben usar redes distintas a la red cuadrada para lograr los umbrales óptimos. [7] [8]
Estos umbrales son límites superiores e inútiles a menos que se encuentren algoritmos eficientes para alcanzarlos. El algoritmo más utilizado es el de coincidencia perfecta de peso mínimo . [9] Cuando se aplica al modelo de ruido con errores de bit y de volteo independientes, se logra un umbral de alrededor del 10,5%. Esto queda solo un poco por debajo del máximo del 11%. Sin embargo, la coincidencia no funciona tan bien cuando hay correlaciones entre los errores de bit y de fase, como con el ruido despolarizante.
Se han considerado los medios para realizar computación cuántica sobre la información lógica almacenada dentro del código tórico, con las propiedades del código proporcionando tolerancia a fallas. Se ha demostrado que extender el espacio estabilizador utilizando "agujeros", vértices o plaquetas en las que no se aplican estabilizadores, permite codificar muchos qubits en el código. Sin embargo, un conjunto universal de puertas unitarias no se puede implementar de manera tolerante a fallas mediante operaciones unitarias y, por lo tanto, se requieren técnicas adicionales para lograr la computación cuántica. Por ejemplo, la computación cuántica universal se puede lograr preparando estados mágicos a través de fragmentos cuánticos codificados llamados tidBits que se usan para teletransportar las puertas adicionales requeridas cuando se reemplazan como un qubit. Además, la preparación de estados mágicos debe ser tolerante a fallas, lo que se puede lograr mediante la destilación de estados mágicos en estados mágicos ruidosos. Se ha encontrado un esquema basado en mediciones para computación cuántica basado en este principio, cuyo umbral de error es el más alto conocido para una arquitectura bidimensional. [10] [11]
Dado que los operadores estabilizadores del código tórico son cuasilocales y actúan solo sobre espines ubicados cerca uno del otro en una red bidimensional, no es irreal definir el siguiente hamiltoniano,
El espacio de estados fundamentales de este hamiltoniano es el espacio estabilizador del código. Los estados excitados corresponden a los de los aniones, con una energía proporcional a su número. Por lo tanto, los errores locales son suprimidos energéticamente por el gap, que ha demostrado ser estable frente a perturbaciones locales. [12] Sin embargo, los efectos dinámicos de tales perturbaciones aún pueden causar problemas para el código. [13] [14]
La brecha también le da al código cierta resistencia a los errores térmicos, lo que le permite corregirlo casi con seguridad durante un tiempo crítico determinado. Este tiempo aumenta con , pero como los aumentos arbitrarios de este acoplamiento no son realistas, la protección que brinda el hamiltoniano aún tiene sus límites.
A menudo se considera la posibilidad de convertir el código tórico, o el código planar, en una memoria cuántica totalmente autocorrectora. La autocorrección significa que el hamiltoniano suprimirá naturalmente los errores de forma indefinida, lo que dará lugar a una vida útil que diverge en el límite termodinámico. Se ha descubierto que esto es posible en el código tórico solo si existen interacciones de largo alcance entre los aniones. [15] [16] Se han hecho propuestas para la realización de estas en el laboratorio. [17] Otro enfoque es la generalización del modelo a dimensiones superiores, con autocorrección posible en 4D con solo interacciones cuasi locales. [18]
Como se mencionó anteriormente, las llamadas y cuasipartículas están asociadas con los vértices y plaquetas del modelo, respectivamente. Estas cuasipartículas pueden describirse como anyones , debido al efecto no trivial de su trenzado. Específicamente, aunque ambas especies de anyones son bosónicos con respecto a sí mismos, el trenzado de dos 's o 's no tiene efecto, una monodromía completa de un y un producirá una fase de . Tal resultado no es consistente con las estadísticas bosónicas o fermiónicas y, por lo tanto, es anyónico.
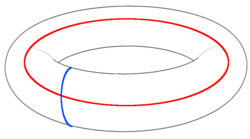
Las estadísticas mutuas anónicas de las cuasipartículas demuestran las operaciones lógicas realizadas por bucles topológicamente no triviales. Considere la creación de un par de aniones seguida del transporte de uno alrededor de un bucle topológicamente no trivial, como el que se muestra en el toro en azul en la figura anterior, antes de que el par se vuelva a anular. El estado se devuelve al espacio estabilizador, pero el bucle implementa una operación lógica en uno de los qubits almacenados. Si los aniones se mueven de manera similar a través del bucle rojo anterior, también se producirá una operación lógica. La fase de resultado al trenzar los aniones muestra que estas operaciones no conmutan, sino que más bien conmutan. Por lo tanto, pueden interpretarse como operadores lógicos y de Pauli en uno de los qubits almacenados. Los Pauli lógicos correspondientes en el otro qubit corresponden a un anion que sigue el bucle azul y a un anion que sigue el rojo. No se produce ningún trenzado cuando y pasan por caminos paralelos, la fase de por lo tanto no surge y las operaciones lógicas correspondientes conmutan. Esto es como se debería esperar, ya que estas operaciones de formación actúan sobre diferentes qubits.
Debido al hecho de que tanto los anyones como los anyones pueden crearse en pares, es claro ver que ambas cuasipartículas son sus propias antipartículas. Una partícula compuesta formada por dos anyones es, por lo tanto, equivalente al vacío, ya que el vacío puede producir un par de este tipo y dicho par se aniquilará en el vacío. En consecuencia, estos compuestos tienen estadísticas bosónicas, ya que su trenzado es siempre completamente trivial. Un compuesto de dos anyones es, de manera similar, equivalente al vacío. La creación de tales compuestos se conoce como la fusión de anyones, y los resultados pueden escribirse en términos de reglas de fusión. En este caso, estas toman la forma,
Donde denota el vacío. Un compuesto de an y an no es trivial. Por lo tanto, esto constituye otra cuasipartícula en el modelo, a veces denotada , con regla de fusión,
A partir de las estadísticas de trenzado de los aniones, vemos que, dado que cualquier intercambio de dos implicará una monodromía completa de un constituyente y , resultará una fase de . Esto implica autoestadística fermiónica para los .
No es necesario el uso de un toro para formar un código de corrección de errores. También se pueden utilizar otras superficies, cuyas propiedades topológicas determinan la degeneración del espacio estabilizador. En general, los códigos de corrección de errores cuánticos definidos en redes de espín bidimensionales según los principios anteriores se conocen como códigos de superficie. [19]
También es posible definir códigos similares utilizando espines de dimensiones superiores. Se trata de los modelos de dobles cuánticos [20] y los modelos de red de cuerdas [21] , que permiten una mayor riqueza en el comportamiento de los anyones, por lo que pueden utilizarse para propuestas de computación cuántica y corrección de errores más avanzadas [22] . Estos no sólo incluyen modelos con anyones abelianos, sino también aquellos con estadísticas no abelianas [23] [24] [25]
La demostración más explícita de las propiedades del código tórico se ha realizado mediante métodos basados en estados. En lugar de intentar realizar el hamiltoniano, estos métodos simplemente preparan el código en el espacio estabilizador. Mediante el uso de esta técnica, los experimentos han podido demostrar la creación, el transporte y las estadísticas de los aniones [26] [27] [28] y la medición de la entropía de entrelazamiento topológico . [28] Experimentos más recientes también han podido demostrar las propiedades de corrección de errores del código. [29] [28]
Se ha avanzado mucho en la realización del código tórico y su generalización con un hamiltoniano mediante uniones Josephson . Se ha desarrollado una teoría de cómo se pueden implementar los hamiltonianos para una amplia clase de códigos topológicos. [30] También se ha realizado un experimento para realizar el hamiltoniano de código tórico para una red pequeña y demostrar la memoria cuántica que proporciona su estado fundamental degenerado. [31]
Otros trabajos teóricos y experimentales para la realización de estos códigos se basan en átomos fríos. Se ha explorado un conjunto de métodos que pueden utilizarse para realizar códigos topológicos con redes ópticas, [32] al igual que experimentos relacionados con instancias mínimas de orden topológico. [33] Tales instancias mínimas del código tórico se han realizado experimentalmente dentro de plaquetas cuadradas aisladas. [34] También se están realizando avances en simulaciones del modelo tórico con átomos de Rydberg , en los que se pueden demostrar el hamiltoniano y los efectos del ruido disipativo. [35] [36] Los experimentos en matrices de átomos de Rydberg también han realizado con éxito el código tórico con condiciones de contorno periódicas en dos dimensiones mediante el transporte coherente de matrices de átomos enredados. [37]