Búsqueda en amplitud

Ejemplo animado de una búsqueda en amplitud. Negro: explorado, gris: en cola para explorar más adelante

Parte superior del árbol del juego del tres en raya

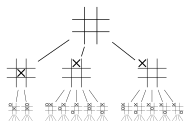
La búsqueda en amplitud ( BFS ) es un algoritmo para buscar en una estructura de datos de árbol un nodo que satisfaga una propiedad determinada. Comienza en la raíz del árbol y explora todos los nodos en la profundidad actual antes de pasar a los nodos del siguiente nivel de profundidad. Se necesita memoria adicional, normalmente una cola , para realizar un seguimiento de los nodos secundarios que se encontraron pero que aún no se exploraron.

Por ejemplo, en un final de ajedrez , un motor de ajedrez puede construir el árbol de juego a partir de la posición actual aplicando todos los movimientos posibles y usar una búsqueda en amplitud para encontrar una posición ganadora para las blancas. Los árboles implícitos (como los árboles de juego u otros árboles de resolución de problemas) pueden tener un tamaño infinito; se garantiza que la búsqueda en amplitud encontrará un nodo de solución ^[1] si existe uno.

Por el contrario, la búsqueda en profundidad (simple) (DFS), que explora la rama del nodo lo más lejos posible antes de retroceder y expandir otros nodos, ^[2] puede perderse en una rama infinita y nunca llegar al nodo de solución. La búsqueda en profundidad con profundización iterativa evita este último inconveniente al precio de explorar las partes superiores del árbol una y otra vez. Por otro lado, ambos algoritmos de búsqueda en profundidad suelen requerir mucha menos memoria adicional que la búsqueda en amplitud. ^[3]

La búsqueda en amplitud se puede generalizar tanto a gráficos no dirigidos como a gráficos dirigidos con un nodo de inicio determinado (a veces denominado "clave de búsqueda"). ^[4] En la búsqueda en el espacio de estados en inteligencia artificial , a menudo se permiten búsquedas repetidas de vértices, mientras que en el análisis teórico de algoritmos basados en la búsqueda en amplitud, normalmente se toman precauciones para evitar repeticiones.

BFS y su aplicación para encontrar componentes conectados de grafos fueron inventados en 1945 por Konrad Zuse , en su tesis doctoral (rechazada) sobre el lenguaje de programación Plankalkül , pero esta no se publicó hasta 1972. ^[5] Fue reinventado en 1959 por Edward F. Moore , quien lo utilizó para encontrar el camino más corto para salir de un laberinto, ^[6]^[7] y luego desarrollado por CY Lee en un algoritmo de enrutamiento de cables (publicado en 1961). ^[8]

Pseudocódigo

Entrada : Un gráfico $G$ y una $raíz de$ vértice inicial de $G$

Salida : Estado objetivo. Los enlaces principales trazan el camino más corto hasta $la raíz$ ^[9]

1 procedimiento BFS( G , raíz ) es 2 sea Q una cola 3 etiqueta raíz como se exploró 4 Q .enqueue( raíz ) 5 mientras  Q no esté vacío hacer 6 v  := Q .dequeue() 7 si  v es el objetivo , entonces 8 devuelve  v 9 para todos los bordes desde v hasta w  en  G .adjacentEdges( v ) hace
10 si  w no está etiquetado como explorado, entonces
11 etiqueta w como explorado12 w .parent := v
13 Q .enqueue( w )

Más detalles

Esta implementación no recursiva es similar a la implementación no recursiva de la búsqueda en profundidad , pero se diferencia de ella en dos formas:

utiliza una cola ( primero en entrar, primero en salir ) en lugar de una pila (último en entrar, primero en salir) y
Comprueba si se ha explorado un vértice antes de ponerlo en cola en lugar de retrasar esta comprobación hasta que el vértice se saque de la cola.

Si $G$ es un árbol , reemplazar la cola de este algoritmo de búsqueda en amplitud por una pila producirá un algoritmo de búsqueda en profundidad. Para los grafos generales, reemplazar la pila de la implementación iterativa de búsqueda en profundidad por una cola también produciría un algoritmo de búsqueda en amplitud, aunque uno un tanto no estándar. ^[10]

La cola Q contiene la frontera a lo largo de la cual el algoritmo está buscando actualmente.

Los nodos se pueden etiquetar como explorados almacenándolos en un conjunto o mediante un atributo en cada nodo, según la implementación.

Tenga en cuenta que la palabra nodo suele ser intercambiable con la palabra vértice .

El atributo padre de cada nodo es útil para acceder a los nodos en una ruta más corta, por ejemplo, retrocediendo desde el nodo de destino hasta el nodo de inicio, una vez que se ha ejecutado el BFS y se han configurado los nodos predecesores.

La búsqueda en amplitud produce un árbol en amplitud . En el siguiente ejemplo, puede ver cómo se ve un árbol en amplitud .

Ejemplo

El siguiente es un ejemplo del árbol en amplitud obtenido al ejecutar un BFS en ciudades alemanas comenzando desde Frankfurt :

El árbol en amplitud obtenido al ejecutar BFS en el mapa dado y comenzando en Frankfurt

Análisis

Complejidad temporal y espacial

La complejidad temporal se puede expresar como , ya que cada vértice y cada arista se explorarán en el peor de los casos. es el número de vértices y es el número de aristas en el gráfico. Tenga en cuenta que puede variar entre y , dependiendo de qué tan disperso sea el gráfico de entrada. ^[11] $O(|V|+|E|)$ ${\estilo de visualización |V|}$ ${\estilo de visualización |E|}$ $O(|E|)$ ${\estilo de visualización O(1)}$ $O(|V|^{2})$

Cuando se conoce de antemano la cantidad de vértices del gráfico y se utilizan estructuras de datos adicionales para determinar qué vértices ya se agregaron a la cola, la complejidad espacial se puede expresar como , donde es la cantidad de vértices. Esto se suma al espacio requerido para el gráfico en sí, que puede variar según la representación gráfica utilizada por una implementación del algoritmo. $O(|V|)$ $|V|$

Cuando se trabaja con gráficos que son demasiado grandes para almacenarse explícitamente (o infinitos), es más práctico describir la complejidad de la búsqueda en amplitud en términos diferentes: para encontrar los nodos que están a una distancia $d$ del nodo de inicio (medida en número de recorridos de aristas), BFS toma $O (b d + 1)$ tiempo y memoria, donde $b$ es el " factor de ramificación " del gráfico (el grado de salida promedio). ^[12]^{: 81}

Lo completo

En el análisis de algoritmos, se supone que la entrada a la búsqueda en amplitud es un gráfico finito, representado como una lista de adyacencia , una matriz de adyacencia o una representación similar. Sin embargo, en la aplicación de métodos de recorrido de gráficos en inteligencia artificial, la entrada puede ser una representación implícita de un gráfico infinito. En este contexto, un método de búsqueda se describe como completo si se garantiza que encontrará un estado objetivo si existe uno. La búsqueda en amplitud es completa, pero la búsqueda en profundidad no lo es. Cuando se aplica a gráficos infinitos representados implícitamente, la búsqueda en amplitud finalmente encontrará el estado objetivo, pero la búsqueda en profundidad puede perderse en partes del gráfico que no tienen un estado objetivo y nunca regresar. ^[13]

Pedidos BFS

Se dice que una enumeración de los vértices de un gráfico es un ordenamiento BFS si es la salida posible de la aplicación de BFS a este gráfico.

Sea un grafo con vértices. Recordemos que es el conjunto de vecinos de . Sea una lista de elementos distintos de , para , sea el menor tal que sea vecino de , si existe tal , y sea en caso contrario. $G=(V,E)$ $n$ $N(v)$ $v$ $\sigma =(v_{1},\dots ,v_{m})$ $V$ $v\in V\setminus \{v_{1},\dots ,v_{m}\}$ $\nu _{\sigma }(v)$ $i$ $v_{i}$ $v$ $i$ $\infty$

Sea una enumeración de los vértices de . Se dice que la enumeración es un ordenamiento BFS (con origen ) si, para todo , es el vértice tal que es mínimo. De manera equivalente, es un ordenamiento BFS si, para todo con , existe un vecino de tal que . $\sigma =(v_{1},\dots ,v_{n})$ $V$ $\sigma$ $v_{1}$ $1<i\leq n$ $v_{i}$ $w\in V\setminus \{v_{1},\dots ,v_{i-1}\}$ $\nu _{(v_{1},\dots ,v_{i-1})}(w)$ $\sigma$ $1\leq i<j<k\leq n$ $v_{i}\in N(v_{k})\setminus N(v_{j})$ $v_{m}$ $v_{j}$ $m<i$

Aplicaciones

La búsqueda en amplitud se puede utilizar para resolver muchos problemas en teoría de grafos, por ejemplo:

Copia de la recolección de basura , algoritmo de Cheney
Encontrar la ruta más corta entre dos nodos u y v , con la longitud de la ruta medida por el número de aristas (una ventaja sobre la búsqueda en profundidad ) ^[14]
(Reverso) Numeración de malla Cuthill–McKee
Método de Ford-Fulkerson para calcular el caudal máximo en una red de flujo
La serialización/deserialización de un árbol binario frente a la serialización en orden ordenado, permite reconstruir el árbol de manera eficiente.
Construcción de la función de fallo del comparador de patrones Aho-Corasick .
Prueba de bipartidismo de un gráfico .
Implementación de algoritmos paralelos para calcular el cierre transitivo de un gráfico. ^[15]

Véase también

Referencias

^ es decir, un nodo que satisface la propiedad especificada
^ Cormen Thomas H.; et al. (2009). "22.3". Introducción a los algoritmos . MIT Press.
^ Korf, Richard E. (1985). "Profundización iterativa en profundidad: una búsqueda de árbol admisible óptima". Inteligencia artificial (27): 99–100. doi :10.7916/D8HQ46X1.
^ "Especificación de referencia Graph500 (evaluación del rendimiento de supercomputadoras)". Graph500.org, 2010. Archivado desde el original el 26 de marzo de 2015. Consultado el 15 de marzo de 2015 .
^ Zuse, Konrad (1972), Der Plankalkül (en alemán), Konrad Zuse Internet Archive. Véanse las páginas 96-105 del archivo pdf vinculado (numeración interna 2.47-2.56).
^ Moore, Edward F. (1959). "El camino más corto a través de un laberinto". Actas del Simposio Internacional sobre la Teoría de la Conmutación . Harvard University Press. págs. 285–292.Según citan Cormen, Leiserson, Rivest y Stein.
^ Skiena, Steven (2008). "Ordenamiento y búsqueda". Manual de diseño de algoritmos . Springer. pág. 480. Bibcode :2008adm..book.....S. doi :10.1007/978-1-84800-070-4_4. ISBN 978-1-84800-069-8.
^ Lee, CY (1961). "Un algoritmo para conexiones de caminos y sus aplicaciones". IRE Transactions on Electronic Computers (3): 346–365. doi :10.1109/TEC.1961.5219222. S2CID 40700386.
^ Cormen, Thomas H. "22.2 Búsqueda en amplitud". Introducción a los algoritmos. ISBN 978-81-203-4007-7.OCLC 1006880283 .
^ "Recorrido de grafos basado en pila ≠ búsqueda en profundidad". 11011110.github.io . Consultado el 10 de junio de 2020 .
^ Cormen, Thomas H. ; Leiserson, Charles E. ; Rivest, Ronald L. ; Stein, Clifford (2001) [1990]. "22.2 Búsqueda en amplitud". Introducción a los algoritmos (2.ª ed.). MIT Press y McGraw-Hill. págs. 531–539. ISBN 0-262-03293-7.
^ Russell, Stuart ; Norvig, Peter (2003) [1995]. Inteligencia artificial: un enfoque moderno (2.ª ed.). Prentice Hall. ISBN 978-0137903955.
^ Coppin, B. (2004). Inteligencia artificial iluminada. Jones & Bartlett Learning. págs. 79–80.
^ Aziz, Adnan; Prakash, Amit (2010). "4. Algoritmos sobre grafos". Algoritmos para entrevistas . p. 144. ISBN 978-1453792995.
^ Dhulipala, Laxman; Blelloch, Guy E.; Shun, Julian (21 de agosto de 2019). Los algoritmos de gráficos paralelos teóricamente eficientes pueden ser rápidos y escalables . pág. 17. arXiv : 1805.05208 . doi :10.1145/3210377.3210414. ISBN . 9781450357999. Número de identificación del sujeto 44126609.

Knuth, Donald E. (1997), El arte de la programación informática, vol. 1, 3.ª ed., Boston: Addison-Wesley, ISBN 978-0-201-89683-1, archivado desde el original el 4 de septiembre de 2008 , consultado el 9 de febrero de 2008

Enlaces externos

Estructuras de datos abiertas - Sección 12.3.1 - Búsqueda en amplitud, Pat Morin