La acústica del piano es el conjunto de propiedades físicas del piano que afectan a su sonido . Es un área de estudio dentro de la acústica musical .

Las cuerdas de un piano varían en diámetro y, por lo tanto, en masa por longitud, siendo las cuerdas más graves más gruesas que las superiores. Un rango típico va desde 0,240 pulgadas (6,1 mm) para las cuerdas graves más graves [1] hasta 0,031 pulgadas (0,79 mm), tamaño de cuerda 13, para las cuerdas agudas más agudas. Estas diferencias en el grosor de las cuerdas se derivan de las propiedades acústicas bien entendidas de las cuerdas.
Si se tienen dos cuerdas igualmente tensas y pesadas, una de ellas el doble de larga que la otra, la más larga vibrará con un tono una octava más bajo que la más corta. Sin embargo, si se utilizara este principio para diseñar un piano, es decir, si se empezara con las notas más altas y luego se duplicara la longitud de las cuerdas una y otra vez para cada octava más baja, sería imposible colocar las cuerdas graves en un marco de un tamaño razonable. Además, cuando las cuerdas vibran, la amplitud de las vibraciones está relacionada con la longitud de las cuerdas; en un hipotético piano ultralargo, las cuerdas más graves chocarían entre sí al tocarlas. En cambio, los fabricantes de pianos aprovechan el hecho de que una cuerda pesada vibra más lentamente que una cuerda ligera de longitud y tensión idénticas; por lo tanto, las cuerdas graves del piano son más cortas de lo que predeciría la regla de "duplicar con cada octava", y son mucho más gruesas que las demás.
El otro factor que afecta el tono, además de la longitud, la densidad y la masa, es la tensión. La tensión de cada cuerda de un piano de cola de concierto puede ser de un promedio de 200 libras (91 kg) y tener una tensión acumulada que supere las 20 toneladas (20 000 kg) cada una.
Cualquier cosa que vibre produce vibraciones en un número de frecuencias por encima del tono fundamental. Estas se llaman sobretonos . Cuando los sobretonos son múltiplos enteros (por ejemplo, 2×, 3× ... 6× ... ) de la frecuencia fundamental (llamados armónicos ), entonces, despreciando la amortiguación , la oscilación es periódica, es decir, vibra exactamente de la misma manera una y otra vez. A muchos les gusta el sonido de las oscilaciones periódicas; por esta razón, muchos instrumentos musicales, incluidos los pianos, están diseñados para producir oscilaciones casi periódicas, es decir, para tener sobretonos lo más cercanos posible a los armónicos del tono fundamental.
En una cuerda vibrante ideal, cuando la longitud de onda de una onda en una cuerda estirada es mucho mayor que el grosor de la cuerda (el ideal teórico es una cuerda de grosor cero y resistencia a la flexión cero), la velocidad de la onda en la cuerda es constante y los sobretonos están en los armónicos. Por eso muchos instrumentos están construidos con cuerdas delgadas o delgadas columnas de aire.
Sin embargo, para los armónicos altos con longitudes de onda cortas que se acercan al diámetro de la cuerda, la cuerda se comporta más como una barra de metal gruesa: su resistencia mecánica a la flexión se convierte en una fuerza adicional a la tensión, que "eleva el tono" de los armónicos. Solo cuando la fuerza de flexión es mucho menor que la tensión de la cuerda, su velocidad de onda (y los armónicos afinados como armónicos) no cambian. Los armónicos de frecuencia elevada (por encima de los armónicos), llamados "parciales", pueden producir un efecto desagradable llamado inarmonicidad . Las estrategias básicas para reducir la inarmonicidad incluyen disminuir el grosor de la cuerda o aumentar su longitud, elegir un material flexible con una fuerza de flexión baja y aumentar la fuerza de tensión para que permanezca mucho mayor que la fuerza de flexión.
El enrollado de una cuerda permite reducir eficazmente el grosor de la misma. En una cuerda entorchada, solo el núcleo interno resiste la flexión, mientras que el enrollado funciona únicamente para aumentar la densidad lineal de la cuerda. El grosor del núcleo interno está limitado por su resistencia y por su tensión; los materiales más resistentes permiten utilizar núcleos más delgados a tensiones más altas, lo que reduce la inarmonicidad. Por ello, los diseñadores de pianos eligen acero de alta calidad para sus cuerdas, ya que su resistencia y durabilidad les ayudan a minimizar los diámetros de las cuerdas.
Si el diámetro de las cuerdas, la tensión, la masa, la uniformidad y la longitud fueran los únicos factores a considerar, todos los pianos podrían ser instrumentos pequeños, del tamaño de una espineta. Sin embargo, los constructores de pianos han descubierto que las cuerdas más largas aumentan la potencia, la armonicidad y la reverberación del instrumento, y ayudan a producir una escala de afinación temperada correctamente.
Con cuerdas más largas, los pianos más grandes logran las longitudes de onda y las características tonales deseadas. Los diseñadores de pianos se esfuerzan por colocar las cuerdas más largas posibles dentro del estuche; además, en igualdad de condiciones, el comprador de pianos sensato intenta obtener el instrumento más grande compatible con el presupuesto y el espacio.
La inarmonicidad aumenta continuamente a medida que las notas se alejan del centro del piano y es uno de los límites prácticos del rango total del instrumento. Las cuerdas más graves, que son necesariamente las más largas, son las más limitadas por el tamaño del piano. El diseñador de un piano corto se ve obligado a utilizar cuerdas gruesas para aumentar la densidad de masa y, por lo tanto, se ve obligado a aceptar una mayor inarmonicidad.
Las cuerdas más agudas deben estar sometidas a la mayor tensión, pero también deben ser lo suficientemente delgadas para permitir una baja densidad de masa. La resistencia limitada del acero (es decir, una cuerda demasiado delgada se romperá bajo la tensión) obliga al diseñador de pianos a utilizar cuerdas muy cortas y ligeramente más gruesas, cuyas longitudes de onda cortas generan inarmonía.
El afinador aprovecha la inarmonicidad natural de un piano para realizar pequeños ajustes en la afinación. El afinador estira las notas, agudizando ligeramente las notas altas y bemolizando las notas bajas para que los armónicos de las notas más bajas tengan la misma frecuencia que los tonos fundamentales de las notas más altas.
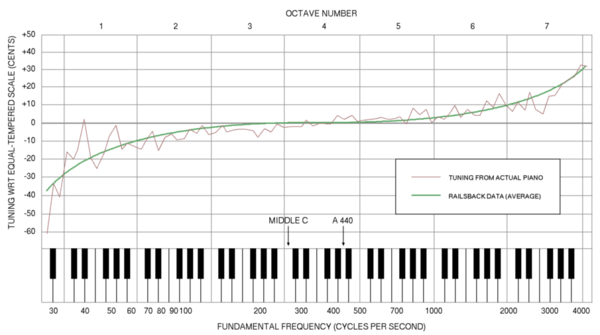
La curva de Railsback , medida por primera vez en la década de 1930 por OL Railsback, un profesor de física de una universidad estadounidense, expresa la diferencia entre una afinación de piano estirada que tiene en cuenta la inarmonicidad y una afinación de temperamento igual teóricamente correcta en la que las frecuencias de notas sucesivas están relacionadas por una relación constante, igual a la raíz duodécima de dos . Para cualquier nota dada en el piano , la desviación entre el tono real de esa nota y su tono de temperamento igual teórico se da en centésimas (centésimas de semitono ). La curva se deriva empíricamente de pianos reales afinados para que sean agradables al oído, no de una ecuación matemática exacta. [2]
Como muestra la curva de Railsback, las octavas normalmente se estiran en un piano bien afinado. Es decir, las notas altas se afinan más alto y las notas bajas más bajo que en una escala de temperamento igual idealizada matemáticamente. Railsback descubrió que los pianos se afinaban típicamente de esta manera no por falta de precisión, sino por la inarmonicidad de las cuerdas. Para una cuerda que vibra como un oscilador armónico ideal , la serie de armónicos de una sola nota tocada incluye muchas frecuencias más altas adicionales, cada una de las cuales es un múltiplo entero de la frecuencia fundamental . Pero, de hecho, la inarmonicidad causada por las cuerdas del piano que son ligeramente inflexibles hace que los armónicos producidos en realidad sean sucesivamente más altos de lo que serían si la cuerda fuera perfectamente armónica .
La falta de armonía en una cuerda se debe principalmente a la rigidez. Esa rigidez es el resultado de la dureza y ductilidad inherentes del alambre de piano, junto con la tensión, el grosor y la longitud de la cuerda. Cuando los afinadores ajustan la tensión del alambre durante la afinación, establecen tonos relativos a las notas que ya se han afinado. Esas notas afinadas previamente tienen armónicos que se agudizan por la falta de armonía, lo que hace que el tono recién establecido se ajuste al armónico agudizado. A medida que la afinación avanza hacia arriba y hacia abajo en la escala, la falta de armonía, y por lo tanto el estiramiento, se acumula.
Es un error muy común pensar que la curva de Railsback demuestra que la parte media del piano es menos inarmónica que las regiones superior e inferior. Esto sólo parece así porque es ahí donde comienza la afinación. "Estiramiento" es un término comparativo: por definición, no importa con qué tono comience la afinación, no puede haber estiramiento. Además, a menudo se interpreta que las notas superiores del piano son especialmente inarmónicas, porque parecen estar estiradas de forma espectacular. De hecho, su estiramiento es un reflejo de la inarmonicidad de las cuerdas en la parte media del piano. Además, la inarmonicidad de las notas superiores no puede tener ninguna relación con la afinación, porque sus parciales superiores están fuera del alcance del oído humano. [3]
Como era de esperar, el gráfico de la afinación real no es una curva suave, sino una línea irregular con picos y valles. Esto podría ser el resultado de una afinación imprecisa, una medición inexacta o la variabilidad innata del piano en la escala de las cuerdas. También se ha sugerido con la simulación de Montecarlo que dicha forma proviene de la forma en que los humanos ajustan los intervalos de tono. [4]
Todas las notas de un piano, excepto las más graves, tienen varias cuerdas afinadas a la misma frecuencia. Las notas con dos cuerdas se denominan bicordios y las de tres cuerdas, tricordios. Estos permiten que el piano tenga un ataque fuerte con una caída rápida pero un sostenido largo en el sistema de ataque-caída-sostenido-liberación (ADSR).
Los tricordios crean un oscilador acoplado con tres modos normales (con dos polarizaciones cada uno). Como las cuerdas están acopladas débilmente, los modos normales tienen frecuencias imperceptiblemente diferentes, pero transfieren su energía vibratoria a la caja de resonancia a velocidades significativamente diferentes.
El modo normal, en el que las tres cuerdas oscilan juntas, es el más eficiente para transferir energía, ya que las tres cuerdas tiran en la misma dirección al mismo tiempo. Suena fuerte, pero decae rápidamente. Este modo normal es responsable de la parte de "ataque" rápido y entrecortado de la nota.
En los otros dos modos normales, las cuerdas no tiran todas juntas, es decir, una tira hacia arriba mientras las otras dos tiran hacia abajo. Hay una transferencia lenta de energía a la caja de resonancia, lo que genera un sustain suave pero casi constante. [5]
...a medida que las frecuencias fundamentales aumentan de tono, también lo hacen sus parciales y en algún punto los parciales de los tonos más altos se vuelven apenas audibles, por lo que su efecto en la afinación sería insignificante.