En estadística y gráficos causales , una variable es un colisionador cuando está influenciada causalmente por dos o más variables. El nombre "colisionador" refleja el hecho de que en los modelos gráficos , las puntas de flecha de las variables que conducen al colisionador parecen "colisionar" en el nodo que es el colisionador. [1] A veces también se las conoce como horquillas invertidas . [2]
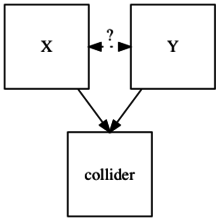
Las variables causales que influyen en el colisionador no están necesariamente asociadas. Si no son adyacentes, el colisionador no está protegido . De lo contrario, el colisionador está protegido y forma parte de un triángulo. [3]
El resultado de tener un colisionador en la trayectoria es que el colisionador bloquea la asociación entre las variables que lo influyen. [4] [5] [6] Por lo tanto, el colisionador no genera una asociación incondicional entre las variables que lo determinan.
El condicionamiento del colisionador mediante análisis de regresión , estratificación, diseño experimental o selección de muestra basada en valores del colisionador crea una asociación no causal entre X e Y ( paradoja de Berkson ). En la terminología de los gráficos causales, el condicionamiento del colisionador abre el camino entre X e Y. Esto introducirá sesgo al estimar la asociación causal entre X e Y , lo que podría introducir asociaciones donde no las hay. Por lo tanto, los colisionadores pueden socavar los intentos de probar teorías causales. [ cita requerida ]
A veces se confunden los colisionadores con las variables de confusión . A diferencia de los colisionadores, las variables de confusión deben controlarse al estimar las asociaciones causales. [ cita requerida ]
Para detectar y gestionar el sesgo del colisionador, los investigadores han utilizado gráficos acíclicos dirigidos . [7]
Los diseños de investigación aleatorizados y cuasiexperimentales no son útiles para superar el sesgo del colisionador. [7]