Reactor continuo de tanque agitado

Diagrama que muestra la configuración de un reactor de tanque agitado continuo

El reactor de tanque agitado continuo ( CSTR ), también conocido como reactor de cuba o de retromezcla , reactor de flujo mixto ( MFR ) o reactor de tanque agitado de flujo continuo ( CFSTR ), es un modelo común para un reactor químico en ingeniería química e ingeniería ambiental . Un CSTR a menudo se refiere a un modelo utilizado para estimar las variables clave de operación unitaria cuando se utiliza un reactor de tanque agitado continuo para alcanzar una salida específica. El modelo matemático funciona para todos los fluidos: líquidos, gases y lodos .

El comportamiento de un CSTR suele aproximarse o modelarse a partir del de un CSTR ideal, que supone una mezcla perfecta . En un reactor perfectamente mezclado, el reactivo se mezcla de manera instantánea y uniforme en todo el reactor al entrar. En consecuencia, la composición de salida es idéntica a la composición del material dentro del reactor, que es una función del tiempo de residencia y la velocidad de reacción. El CSTR es el límite ideal de mezcla completa en el diseño de reactores, que es completamente opuesto a un reactor de flujo pistón (PFR). En la práctica, ningún reactor se comporta de manera ideal, sino que se encuentra en algún punto entre los límites de mezcla de un CSTR ideal y un PFR.

CSTR ideal

Modelado

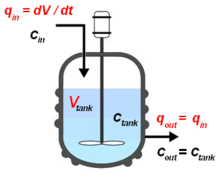
Un flujo de fluido continuo que contiene un reactivo químico no conservativo A ingresa a un CSTR ideal de volumen V.

Supuestos:

mezcla perfecta o ideal
estado estacionario , donde N _A es el número de moles de la especie A ${\Bigl (}{\frac {dN_{A}}{dt}}=0{\Bigr )}$
fronteras cerradas
densidad de fluido constante (válida para la mayoría de los líquidos; válida para gases solo si no hay un cambio neto en el número de moles o un cambio drástico de temperatura)
Reacción de orden ⁿ ( r = kC A _n⁾ , donde k es la constante de velocidad de reacción, C _A es la concentración de la especie A y n es el orden de la reacción.
condiciones isotérmicas o temperatura constante ( k es constante)
reacción única e irreversible ( ν _A = −1)
Todo reactivo A se convierte en productos mediante una reacción química.
NA = CAV

Balance de masa integral sobre el número de moles N _A de la especie A en un reactor de volumen V : $1.[{\text{Acumulación neta de}}~A]=[A~{\text{entrada}}]-[A~{\text{salida}}]+[{\text{Generación neta de}}~A]$

$2.{\frac {dN_{A}}{dt}}=F_{Ao}-F_{A}+V\nu _{A}r_{A}$ ^[1]

dónde

F _Ao es el caudal molar de entrada de la especie A
F _A es el caudal molar de salida de la especie A
v _A es el coeficiente estequiométrico
r _A es la velocidad de reacción

Aplicando los supuestos de estado estacionario y ν _A = −1, la ecuación 2 se simplifica a:

$3.\ 0=F_{Ao}-F_{A}-Vr_{A}$

Los caudales molares de la especie A pueden entonces reescribirse en términos de la concentración de A y el caudal del fluido ( Q ):

$4.\ 0=QC_{Ao}-QC_{A}-Vr_{A}$ ^[2]

La ecuación 4 puede entonces reorganizarse para aislar r _A y simplificarse:

$5.\r_{A}={\frac {Q}{V}}(C_{Ao}-C_{A})$ ^[2]

$6.\r_{A}={\frac {1}{\tau}}(C_{Ao}-C_{A})$

dónde

${\estilo de visualización \tau}$ es el tiempo de residencia teórico ( ) $\tau ={\tfrac {V}{Q}}$
C _Ao es la concentración de entrada de la especie A
C _A es la concentración de la especie A en el reactor/salida

El tiempo de residencia es la cantidad total de tiempo que una cantidad discreta de reactivo pasa dentro del reactor. Para un reactor ideal, el tiempo de residencia teórico, , es siempre igual al volumen del reactor dividido por el caudal del fluido. ^[2] Consulte la siguiente sección para obtener una discusión más detallada sobre la distribución del tiempo de residencia de un CSTR. ${\estilo de visualización \tau}$

Dependiendo del orden de la reacción , la velocidad de reacción, r _A , generalmente depende de la concentración de la especie A en el reactor y de la constante de velocidad. Un supuesto clave al modelar un CSTR es que cualquier reactivo en el fluido está perfectamente (es decir, uniformemente) mezclado en el reactor, lo que implica que la concentración dentro del reactor es la misma en la corriente de salida. ^[3] La constante de velocidad se puede determinar utilizando una velocidad de reacción empírica conocida que se ajusta a la temperatura utilizando la dependencia de la temperatura de Arrhenius . ^[2] Generalmente, a medida que aumenta la temperatura, también lo hace la velocidad a la que ocurre la reacción.

La ecuación 6 se puede resolver por integración después de sustituir la expresión de velocidad adecuada. La siguiente tabla resume la concentración de salida de la especie A para un CSTR ideal. Los valores de la concentración de salida y el tiempo de residencia son criterios de diseño importantes en el diseño de CSTR para aplicaciones industriales.

Distribución del tiempo de residencia

Funciones de distribución de edad de salida E(t) y distribución de edad acumulada F(t) para un CSTR ideal

Un CSTR ideal exhibirá un comportamiento de flujo bien definido que puede caracterizarse por la distribución del tiempo de residencia del reactor o la distribución de la edad de salida. ^[4] No todas las partículas de fluido pasarán la misma cantidad de tiempo dentro del reactor. La distribución de la edad de salida (E(t)) define la probabilidad de que una partícula de fluido dada pase el tiempo t en el reactor. De manera similar, la distribución de la edad acumulada (F(t)) da la probabilidad de que una partícula de fluido dada tenga una edad de salida menor que el tiempo t. ^[3] Una de las conclusiones clave de la distribución de la edad de salida es que una cantidad muy pequeña de partículas de fluido nunca saldrán del CSTR. ^[5] Dependiendo de la aplicación del reactor, esto puede ser una ventaja o una desventaja.

CSTR no ideal

Si bien el modelo CSTR ideal es útil para predecir el destino de los componentes durante un proceso químico o biológico, los CSTR rara vez exhiben un comportamiento ideal en la realidad. ^[2] Lo más común es que la hidráulica del reactor no se comporte de manera ideal o que las condiciones del sistema no obedezcan las suposiciones iniciales. La mezcla perfecta es un concepto teórico que no se puede lograr en la práctica. ^[6] Sin embargo, para fines de ingeniería, si el tiempo de residencia es de 5 a 10 veces el tiempo de mezcla, el supuesto de mezcla perfecta generalmente es válido.

El comportamiento hidráulico no ideal se clasifica comúnmente como espacio muerto o cortocircuito. Estos fenómenos ocurren cuando algún fluido pasa menos tiempo en el reactor que el tiempo de residencia teórico, . La presencia de esquinas o deflectores en un reactor a menudo da como resultado un espacio muerto donde el fluido está mal mezclado. ^[6] De manera similar, un chorro de fluido en el reactor puede causar cortocircuito, en el que una parte del flujo sale del reactor mucho más rápido que el fluido a granel. Si hay espacio muerto o cortocircuito en un CSTR, las reacciones químicas o biológicas relevantes pueden no terminar antes de que el fluido salga del reactor. ^[2] Cualquier desviación del flujo ideal dará como resultado una distribución del tiempo de residencia diferente de la distribución ideal, como se ve a la derecha. ~~${\estilo de visualización \tau}$~~

Modelado de flujo no ideal

Aunque los reactores de flujo ideal rara vez se encuentran en la práctica, son herramientas útiles para modelar reactores de flujo no ideal. Cualquier régimen de flujo se puede lograr modelando un reactor como una combinación de CSTR ideales y reactores de flujo pistón (PFR) ya sea en serie o en paralelo. ^[6] Por ejemplo, una serie infinita de CSTR ideales es hidráulicamente equivalente a un PFR ideal. ^[2] Los modelos de reactor que combinan varios CSTR en serie a menudo se denominan modelos de tanques en serie (TIS). ^[7]

Para modelar sistemas que no obedecen a los supuestos de temperatura constante y una única reacción, se deben considerar variables dependientes adicionales. Si se considera que el sistema está en estado no estacionario, se debe resolver una ecuación diferencial o un sistema de ecuaciones diferenciales acopladas. Las desviaciones del comportamiento de los CSTR se pueden considerar mediante el modelo de dispersión. Se sabe que los CSTR son uno de los sistemas que presentan un comportamiento complejo, como multiplicidad en estado estacionario, ciclos límite y caos.

Cascadas de CSTR

Las cascadas de CSTR, también conocidas como series de CSTR, se utilizan para disminuir el volumen de un sistema. ^[8]

Minimizar el volumen

Como se ve en el gráfico con un CSTR, donde la tasa inversa se representa como una función de la conversión fraccionaria , el área en el cuadro es igual a donde V es el volumen total del reactor y es el caudal molar de la alimentación. Cuando se aplica el mismo proceso a una cascada de CSTR como se ve en el gráfico con tres CSTR, el volumen de cada reactor se calcula a partir de cada conversión fraccionaria de entrada y salida, lo que da como resultado una disminución en el volumen total del reactor. El tamaño óptimo se logra cuando se maximiza el área sobre los rectángulos de los CSTR en serie que anteriormente estaba cubierta por un solo CSTR. Para una reacción de primer orden con dos CSTR, se deben usar volúmenes iguales. A medida que el número de CSTR ideales (n) se acerca al infinito, el volumen total del reactor se acerca al de un PFR ideal para la misma reacción y conversión fraccionaria. ${\frac {V}{F_{Ao}}}$ $Estilo de visualización F_{Ao}}$

Cascada ideal de CSTR

A partir de la ecuación de diseño de un único CSTR donde , podemos determinar que para un único CSTR en serie que , donde es el tiempo espacial del reactor, es la concentración de alimentación de A, es la concentración de salida de A y es la velocidad de reacción de A. $\tau ={\frac {C_{Ao}-C_{A}}{-r_{A}}}$ $\tau _{i}={\frac {C_{A(i-1)}-C_{Ai}}{-r_{Ai}}}$ ${\estilo de visualización \tau}$ $Estilo de visualización C_{Ao}}$ $Estilo de visualización C_{A}}$ $estilo de visualización -r_{A}}$

Primer orden

Para una reacción isotérmica de primer orden y densidad constante en una cascada de CSTR idénticos que operan en estado estacionario

Para un CSTR: , donde k es la constante de velocidad y es la concentración de salida de A del primer CSTR $C_{A1}={\frac {C_{Ao}}{1+k\tau }}$ $Estilo de visualización C_{A1}}$

Dos CSTR: y $C_{A1}={\frac {C_{Ao}}{1+k\tau }}$ $C_{A2}={\frac {C_{A1}}{1+k\tau }}$

Conectando la primera ecuación CSTR a la segunda: $C_{A2}={\frac {C_{Ao}}{(1+k\tau )^{2}}}$

Por lo tanto, para m CSTR idénticos en serie: $C_{Am}={\frac {C_{Ao}}{(1+k\tau )^{m}}}$

Cuando los volúmenes de los CSTR individuales en serie varían, el orden de los CSTR no cambia la conversión general para una reacción de primer orden siempre que los CSTR funcionen a la misma temperatura.

Orden cero

En estado estacionario, la ecuación general para una reacción isotérmica de orden cero en una cascada de CSTR está dada por $C_{Am}=C_{Ao}-\sum _{i=1}^{m}k_{i}\tau _{i}$

Cuando la cascada de CSTR es isotérmica con reactores idénticos, la concentración viene dada por $C_{Am}=C_{Ao}-mk_{i}\tau _{i}$

Segundo orden

Para una reacción isotérmica de segundo orden en estado estacionario en una cascada de CSTR, la ecuación de diseño general es $C_{Ai}={\frac {-1+{\sqrt {1+4k_{i}\tau _{i}C_{A(i-1)}}}}{2k_{i}\tau _{i}}}$

Cascada no ideal de CSTR

Con reactores no ideales, se pueden calcular distribuciones de tiempo de residencia . La concentración en el reactor j en serie viene dada por

${\frac {C_{j}}{C_{o}}}=1-e^{-{\frac {nt}{\bar {t}}}}[1+{\frac {nt}{\bar {t}}}+{\frac {1}{2!}}({\frac {nt}{\bar {t}}})^{2}+...+{\frac {1}{(j-1)!}}({\frac {nt}{\bar {t}}})^{j-1}]$

donde n es el número total de CSTR en serie, y es el tiempo de residencia promedio de la cascada dado por donde Q es el caudal volumétrico . ${\bar {t}}$ ${\bar {t}}={\frac {V}{Q}}$

A partir de esto, la distribución del tiempo de residencia acumulativo (F(t)) se puede calcular como

$F(t)={\frac {C_{n}}{C_{o}}}=1-e^{-{\frac {nt}{\bar {t}}}}[1+{\frac {nt}{\bar {t}}}+{\frac {1}{2!}}({\frac {nt}{\bar {t}}})^{2}+...+{\frac {1}{(n-1)!}}({\frac {nt}{\bar {t}}})^{n-1}]$

A medida que n → ∞, F(t) se acerca a la respuesta PFR ideal. La varianza asociada con F(t) para un estímulo de pulso en una cascada de CSTR es . $\sigma _{t}^{2}={\frac {{\bar {t}}^{2}}{n}}$

Costo

Al determinar el costo de una serie de CSTR, se deben tener en cuenta los costos de capital y de operación . Como se vio anteriormente, un aumento en el número de CSTR en serie disminuirá el volumen total del reactor. Dado que el costo aumenta con el volumen, los costos de capital se reducen al aumentar el número de CSTR. La mayor disminución en el costo, y por lo tanto en el volumen, ocurre entre un solo CSTR y tener dos CSTR en serie. Al considerar el costo de operación, el costo de operación aumenta con el número de bombas y controles, construcción, instalación y mantenimiento que acompañan a las cascadas más grandes. Por lo tanto, a medida que aumenta el número de CSTR, aumenta el costo de operación. Por lo tanto, existe un costo mínimo asociado con una cascada de CSTR.

Reacciones de orden cero

A partir de una reorganización de la ecuación dada para CSTR isotérmicos idénticos que ejecutan una reacción de orden cero: , el volumen de cada CSTR individual se escalará en . Por lo tanto, el volumen total del reactor es independiente del número de CSTR para una reacción de orden cero. Por lo tanto, el costo no es una función del número de reactores para una reacción de orden cero y no disminuye a medida que aumenta el número de CSTR. $\tau ={\frac {C_{Ao}-C_{Am}}{mk}}$ ${\frac {1}{m}}$

Selectividad de reacciones paralelas

Al considerar reacciones paralelas , la utilización de una cascada de CSTR puede lograr una mayor selectividad para un producto deseado.

Para una reacción paralela dada y con constantes y y ecuaciones de velocidad y , respectivamente, podemos obtener una relación entre las dos dividiendo por . Por lo tanto . En el caso donde y B es el producto deseado, la cascada de CSTR se ve favorecida con una alimentación secundaria fresca de para maximizar la concentración de . ${\ce {A -> B}}$ ${\ce {A -> C}}$ $k_{1}$ $k_{2}$ ${\frac {d[{\ce {B}}]}{dt}}=k_{1}[{\ce {A}}]^{n_{1}}$ ${\frac {d[{\ce {C}}]}{dt}}=k_{2}[{\ce {A}}]^{n_{2}}$ ${\frac {d[{\ce {B}}]}{dt}}$ ${\frac {d[{\ce {C}}]}{dt}}$ ${\frac {d[{\ce {B}}]}{d[{\ce {C}}]}}={\frac {k_{1}}{k_{2}}}[{\ce {A}}]^{n_{1}-n_{2}}$ $n_{1}>n_{2}$ ${\ce {A}}$ ${\ce {A}}$

Para una reacción paralela con dos o más reactivos como y con constantes y y ecuaciones de velocidad y , respectivamente, podemos obtener una relación entre los dos dividiendo por . Por lo tanto . En el caso donde y y B es el producto deseado, se favorece una cascada de CSTR con una corriente de entrada de alta y . En el caso donde y y B es el producto deseado, se favorece una cascada de CSTR con una alta concentración de en la alimentación y pequeñas corrientes secundarias de . ^[9] ${\ce {A + D -> B}}$ ${\ce {A + D -> C}}$ $k_{1}$ $k_{2}$ ${\frac {d[{\ce {B}}]}{dt}}=k_{1}[{\ce {A}}]^{n_{1}}[{\ce {D}}]^{m_{1}}$ ${\frac {d[{\ce {C}}]}{dt}}=k_{2}[{\ce {A}}]^{n_{2}}[{\ce {D}}]^{m_{1}2}$ ${\frac {d[{\ce {B}}]}{dt}}$ ${\frac {d[{\ce {C}}]}{dt}}$ ${\frac {d[{\ce {B}}]}{d[{\ce {C}}]}}={\frac {k_{1}}{k_{2}}}[{\ce {A}}]^{n_{1}-n_{2}}[{\ce {D}}]^{m_{1}-m_{2}}$ $n_{1}>n_{2}$ $m_{1}>m_{2}$ ${\ce {[A]}}$ ${\ce {[D]}}$ $n_{1}>n_{2}$ $m_{1}<m_{2}$ ${\ce {A}}$ ${\ce {D}}$

Las reacciones en serie, como también tienen selectividad entre y pero, en general, los CSTR no suelen elegirse cuando el producto deseado es, ya que la retromezcla del CSTR favorece . Normalmente, se elige un reactor discontinuo o PFR para estas reacciones. ${\ce {A -> B -> C}}$ ${\ce {B}}$ ${\ce {C}}$ ${\ce {B}}$ ${\ce {C}}$

Aplicaciones

Los CSTR facilitan la dilución rápida de reactivos a través de la mezcla. Por lo tanto, para reacciones de orden distinto de cero, la baja concentración de reactivo en el reactor significa que un CSTR será menos eficiente en la eliminación del reactivo en comparación con un PFR con el mismo tiempo de residencia. ^[3] Por lo tanto, los CSTR suelen ser más grandes que los PFR, lo que puede ser un desafío en aplicaciones donde el espacio es limitado. Sin embargo, uno de los beneficios adicionales de la dilución en los CSTR es la capacidad de neutralizar los choques en el sistema. A diferencia de los PFR, el rendimiento de los CSTR es menos susceptible a los cambios en la composición del influente, lo que lo hace ideal para una variedad de aplicaciones industriales:

Ingeniería ambiental

Proceso de lodos activados para el tratamiento de aguas residuales ^[2]
Sistemas de tratamiento de lagunas para el tratamiento natural de aguas residuales ^[2]
Digestores anaeróbicos para la estabilización de biosólidos de aguas residuales ^[10]
Humedales de tratamiento de aguas residuales y de escorrentía pluvial ^[11]

Ingeniería química

Reactor de bucle para la producción de productos farmacéuticos ^[12]

Fermentación ^[12]
Producción de biogás

Véase también

Notas

Referencias

^ ab Schmidt, Lanny D. (1998). La ingeniería de las reacciones químicas . Nueva York: Oxford University Press. ISBN 0-19-510588-5.
^ abcdefghi Metcalf & Eddy (3 de septiembre de 2013). Ingeniería de aguas residuales: tratamiento y recuperación de recursos . Tchobanoglous, George, Stensel, H. David, Tsuchihashi, Ryujiro, Burton, Franklin L. (Franklin Louis), 1927-, Abu-Orf, Mohammad, Bowden, Gregory (quinta edición). Nueva York, NY. ISBN 978-0-07-340118-8.OCLC 858915999 .{{cite book}}: CS1 maint: location missing publisher (link)
^ abc Benjamin, Mark M. (13 de junio de 2013). Ingeniería de la calidad del agua: procesos de tratamiento físico-químico . Lawler, Desmond F. Hoboken, Nueva Jersey. ISBN 978-1-118-63227-7.OCLC 856567226 .{{cite book}}: CS1 maint: location missing publisher (link)
^ Bolin, Bert; Rodhe, Henning (enero de 1973). "Una nota sobre los conceptos de distribución de edades y tiempo de tránsito en embalses naturales". Tellus . 25 (1): 58–62. Bibcode : 1973 Dile...25...58B. doi : 10.3402/tellusa.v25i1.9644 . ISSN 0040-2826.
^ Monsen, Nancy E.; Cloern, James E.; Lucas, Lisa V.; Monismith, Stephen G. (septiembre de 2002). "Un comentario sobre el uso del tiempo de descarga, el tiempo de residencia y la edad como escalas de tiempo de transporte". Limnología y Oceanografía . 47 (5): 1545–1553. Bibcode :2002LimOc..47.1545M. doi : 10.4319/lo.2002.47.5.1545 . S2CID 11505988.
^ abc Davis, Mark E. (2003). Fundamentos de la ingeniería de reacciones químicas . Davis, Robert J. (ed. internacional). Boston: McGraw-Hill. ISBN 978-1-62870-437-2.OCLC 880604539 .
^ Stokes, RL; Nauman, E. Bruce (1970). "Funciones de distribución del tiempo de residencia para tanques agitados en serie". Revista canadiense de ingeniería química . 48 (6): 723–725.
^ Hill, Charles G.; Root, Thatcher W. (2014). Introducción a la cinética de la ingeniería química y diseño de reactores, segunda edición . Hoboken, Nueva Jersey: Wiley. págs. 241–253, 349–358. ISBN 9781118368251.
^ Levenspiel, Octave (1998). Ingeniería de reacciones químicas, 3.ª edición . Wiley. ISBN 978-0-471-25424-9.
^ Hurtado, FJ; Kaiser, AS; Zamora, B. (marzo de 2015). "Análisis fluidodinámico de un reactor de tanque agitado continuo para la optimización técnica de la digestión de aguas residuales". Water Research . 71 : 282–293. Bibcode :2015WatRe..71..282H. doi :10.1016/j.watres.2014.11.053. ISSN 0043-1354. PMID 25635665.
^ Kadlec, Robert H.; Wallace, Scott D. (2009). Tratamiento de humedales (segunda ed.). Boca Ratón, FL, Estados Unidos: CRC Press. pag. 181.ISBN 978-1-56670-526-4.
^ ab "Enciclopedia visual de ingeniería química". encyclopedia.che.engin.umich.edu . Archivado desde el original el 14 de diciembre de 2013 . Consultado el 30 de abril de 2020 .