
En informática y matemáticas, la confluencia es una propiedad de la reescritura de sistemas, que describe qué términos de dicho sistema se pueden reescribir de más de una forma para producir el mismo resultado. Este artículo describe las propiedades en la configuración más abstracta de un sistema de reescritura abstracta .
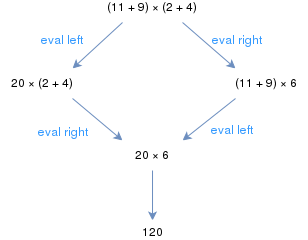
Las reglas habituales de la aritmética elemental forman un sistema de reescritura abstracto. Por ejemplo, la expresión (11 + 9) × (2 + 4) se puede evaluar comenzando por el paréntesis izquierdo o derecho; sin embargo, en ambos casos finalmente se obtiene el mismo resultado. Si cada expresión aritmética da el mismo resultado independientemente de la estrategia de reducción, se dice que el sistema de reescritura aritmética es confluente. Los sistemas de reescritura aritmética pueden ser confluentes o sólo confluentes en tierra dependiendo de los detalles del sistema de reescritura. [1]
Un segundo ejemplo, más abstracto, se obtiene de la siguiente prueba de que cada elemento de grupo es igual al inverso de su inverso: [2]
Esta prueba parte de los axiomas del grupo dado A1-A3 y establece cinco proposiciones R4, R6, R10, R11 y R12, cada una de las cuales utiliza algunas anteriores, siendo R12 el teorema principal. Algunas de las demostraciones requieren pasos no obvios, o incluso creativos, como aplicar el axioma A2 a la inversa, reescribiendo así "1" como " a −1 ⋅ a" en el primer paso de la demostración de R6. Una de las motivaciones históricas para desarrollar la teoría de la reescritura de términos fue evitar la necesidad de tales pasos, que son difíciles de encontrar para un ser humano sin experiencia, y mucho menos para un programa de computadora [ cita requerida ] .
Si un sistema de reescritura de términos es confluente y termina , existe un método sencillo para demostrar la igualdad entre dos expresiones (también conocidas como términos ) s y t : comenzando con s , aplique igualdades [nota 1] de izquierda a derecha tanto como sea posible, eventualmente obteniendo un término s′ . Obtenga de t un término t′ de manera similar. Si ambos términos s′ y t′ concuerdan literalmente, entonces se demuestra que s y t son iguales. Más importante aún, si no están de acuerdo, entonces s y t no pueden ser iguales. Es decir, dos términos cualesquiera s y t que puedan demostrarse iguales pueden hacerlo mediante ese método.
El éxito de ese método no depende de un cierto orden sofisticado en el cual aplicar reglas de reescritura, ya que la confluencia asegura que cualquier secuencia de aplicaciones de reglas eventualmente conducirá al mismo resultado (mientras que la propiedad de terminación asegura que cualquier secuencia eventualmente llegará a un final). en absoluto). Por lo tanto, si se puede proporcionar un sistema de reescritura de términos confluente y terminal para alguna teoría ecuacional , [nota 2] no se requiere ni un ápice de creatividad para realizar pruebas de igualdad de términos; por lo tanto, esa tarea se vuelve susceptible de ser ejecutada por programas de computadora. Los enfoques modernos manejan sistemas de reescritura abstracta más generales en lugar de sistemas de reescritura de términos ; estos últimos son un caso especial de los primeros.

Un sistema de reescritura se puede expresar como un gráfico dirigido en el que los nodos representan expresiones y los bordes representan reescrituras. Entonces, por ejemplo, si la expresión a se puede reescribir en b , entonces decimos que b es una reducción de a (alternativamente, a se reduce a b , o a es una expansión de b ). Esto se representa mediante notación de flechas; a → b indica que a se reduce a b . Intuitivamente, esto significa que el gráfico correspondiente tiene un borde dirigido de a a b .
Si hay un camino entre dos nodos del gráfico cyd , entonces se forma una secuencia de reducción . Entonces, por ejemplo, si c → c′ → c′′ → ... → d′ → d , entonces podemos escribir c d , indicando la existencia de una secuencia de reducción de c a d . Formalmente,es la clausura reflexivo-transitiva de →. Usando el ejemplo del párrafo anterior, tenemos (11+9)×(2+4) → 20×(2+4) y 20×(2+4) → 20×6, entonces (11+9)×( 2+4)20×6.
Una vez establecido esto, la confluencia se puede definir de la siguiente manera. a ∈ S se considera confluente si para todos los pares b , c ∈ S tales que a b y a c , existe a d ∈ S con b d y c d (denotado ). Si todo a ∈ S es confluente, decimos que → es confluente. Esta propiedad a veces también se denomina propiedad del diamante , por la forma del diagrama que se muestra a la derecha. Algunos autores reservan el término propiedad del diamante para una variante del diagrama con reducciones únicas en todas partes; es decir, siempre que a → b y a → c , debe existir un d tal que b → d y c → d . La variante de reducción única es estrictamente más fuerte que la de reducción múltiple.
Un sistema de reescritura de términos es confluente si todos los términos básicos son confluentes, es decir, todos los términos sin variables. [3]


Se dice que un elemento a ∈ S es localmente confluente (o débilmente confluente [5] ) si para todo b , c ∈ S con a → b y a → c existe d ∈ S con b d y c d . Si cada a ∈ S es localmente confluente, entonces → se llama localmente confluente o tiene la propiedad débil de Church-Rosser . Esto se diferencia de la confluencia en que b y c deben reducirse de a en un solo paso. En analogía con esto, a la confluencia a veces se la denomina confluencia global .
La relación, introducido como una notación para secuencias de reducción, puede verse como un sistema de reescritura por derecho propio, cuya relación es el cierre reflexivo-transitivo de → . Dado que una secuencia de secuencias reductoras es nuevamente una secuencia reductora (o, de manera equivalente, dado que formar la clausura reflexivo-transitiva es idempotente ),=. De ello se deduce que → es confluente si y sólo sies localmente confluente.
Un sistema de reescritura puede ser confluente localmente sin serlo (globalmente). Se muestran ejemplos en las imágenes 3 y 4. Sin embargo, el lema de Newman establece que si un sistema de reescritura con confluencia local no tiene secuencias de reducción infinitas (en cuyo caso se dice que es terminante o fuertemente normalizante ), entonces es confluente global.
Se dice que un sistema de reescritura posee la propiedad de Church-Rosser si y sólo si implica para todos los objetos x , y . Alonzo Church y J. Barkley Rosser demostraron en 1936 que el cálculo lambda tiene esta propiedad; [6] de ahí el nombre de la propiedad. [7] (El hecho de que el cálculo lambda tenga esta propiedad también se conoce como teorema de Church-Rosser ). En un sistema de reescritura con la propiedad de Church-Rosser, el problema verbal puede reducirse a la búsqueda de un sucesor común. En un sistema Church-Rosser, un objeto tiene como máximo una forma normal ; es decir, la forma normal de un objeto es única si existe, pero es posible que no exista. En el cálculo lambda, por ejemplo, la expresión (λx.xx)(λx.xx) no tiene una forma normal porque existe una secuencia infinita de β-reducciones (λx.xx)(λx.xx) → (λx.xx) (λx.xx) → ... [8]
Un sistema de reescritura posee la propiedad Church-Rosser si y sólo si es confluente. [9] Debido a esta equivalencia, en la literatura se encuentra bastante variación en las definiciones. Por ejemplo, en "Terese", la propiedad Church-Rosser y la confluencia se definen como sinónimas e idénticas a la definición de confluencia presentada aquí; Church-Rosser, tal como se define aquí, permanece sin nombre, pero se proporciona como una propiedad equivalente; esta desviación de otros textos es deliberada. [10]
La definición de confluencia local difiere de la de confluencia global en que solo se consideran los elementos alcanzados a partir de un elemento determinado en un único paso de reescritura. Considerando un elemento alcanzado en un solo paso y otro elemento alcanzado mediante una secuencia arbitraria, llegamos al concepto intermedio de semiconfluencia: se dice que a ∈ S es semiconfluente si para todo b , c ∈ S con a → b y a c existe d ∈ S con b d y c d ; si todo a ∈ S es semiconfluente, decimos que → es semiconfluente.
Un elemento semiconfluente no tiene por qué ser confluente, pero un sistema de reescritura semiconfluente es necesariamente confluente, y un sistema confluente es trivialmente semiconfluente.
La confluencia fuerte es otra variación de la confluencia local que nos permite concluir que un sistema de reescritura es confluente globalmente. Se dice que un elemento a ∈ S es fuertemente confluente si para todo b , c ∈ S con a → b y a → c existe d ∈ S con b d y c → d o c = d ; si cada a ∈ S es fuertemente confluente, decimos que → es fuertemente confluente.
Un elemento confluente no tiene por qué ser fuertemente confluente, pero un sistema de reescritura fuertemente confluente es necesariamente confluente.