En la música que utiliza la técnica de doce tonos , la combinatoria es una cualidad compartida por las filas de tonos de doce tonos por las cuales cada sección de una fila y un número proporcional de sus transformaciones se combinan para formar agregados (los doce tonos). [1] Así como los tonos de un agregado creado por una fila de tonos no necesitan ocurrir simultáneamente, los tonos de un agregado creado combinatoriamente no necesitan ocurrir simultáneamente. Arnold Schoenberg , creador de la técnica de doce tonos, a menudo combinaba P-0/I-5 para crear "dos agregados, entre los primeros hexacordos de cada uno y los segundos hexacordos de cada uno, respectivamente". [1]
La combinatoria es un efecto secundario de las filas derivadas , donde el segmento o conjunto inicial puede combinarse con sus transformaciones (T, R, I, RI) para crear una fila entera. "La derivación se refiere a un proceso mediante el cual, por ejemplo, el tricordio inicial de una fila puede usarse para llegar a una nueva fila 'derivada' empleando las operaciones estándar de doce tonos de transposición , inversión , retrógrada e inversión retrógrada ". [2]
Las propiedades combinatorias no dependen del orden de las notas dentro de un conjunto, sino solo del contenido del conjunto, y la combinatoria puede existir entre tres conjuntos tetracordales y entre cuatro conjuntos tricordales , así como entre pares de hexacordios, [3] y seis díadas . [4] Un complemento en este contexto es la mitad de un conjunto de clases de tonos combinatorios y, en general, es la "otra mitad" de cualquier par, incluidos los conjuntos de clases de tonos, las texturas o el rango de tonos.
En términos más generales, la complementación es la separación de conjuntos de clases de tono en dos conjuntos complementarios, uno de los cuales contiene las clases de tono que no están en el otro. [1] De manera más restrictiva, la complementación es "el proceso de emparejar entidades a ambos lados de un centro de simetría". [5]
El término "combinatorio" parece haber sido aplicado por primera vez a la música dodecafónica por Milton Babbitt en 1950, [7] cuando publicó una reseña de los libros de René Leibowitz Schoenberg et son école y Qu'est-ce que la musique de douze sons? [8] Babbitt también introdujo el término " fila derivada" . [2]

Una fila de 12 tonos tiene combinatoria hexacordal con otra fila de 12 tonos si sus respectivos primeros hexacordios (así como sus segundos, porque una fila de 12 tonos en sí misma forma un agregado por definición) forman un agregado.
Existen cuatro tipos principales de combinatoria. Un hexacordio puede ser:
y por lo tanto:
La combinatoria primaria (transposicional) de un hexacordo se refiere a la propiedad de un hexacordo por la cual forma un agregado con una o más de sus transposiciones. Alternativamente, la combinatoria transposicional es la falta de clases de tonos compartidas entre un hexacordo y una o más de sus transposiciones. Por ejemplo, 0 2 4 6 8 t, y su transposición un semitono hacia arriba (+1): 1 3 5 7 9 e, no tienen notas en común.
La combinatoria hexacordal retrógrada se considera trivial, ya que cualquier fila tiene combinatoria hexacordal retrógrada consigo misma ( todas las filas de tonos tienen combinatoria retrógrada).
La combinatoria inversional es una relación entre dos filas, una fila principal y su inversión. La primera mitad de la fila principal, o seis notas, son las últimas seis notas de la inversión, aunque no necesariamente en el mismo orden. Por lo tanto, la primera mitad de cada fila es el complemento de la otra . La misma conclusión se aplica también a la segunda mitad de cada fila. Cuando se combinan, estas filas aún mantienen una sensación completamente cromática y no tienden a reforzar ciertas notas como centros tonales como podría suceder con filas combinadas libremente. Por ejemplo, la fila de Moisés y Aron de Schoenberg , arriba, contiene: 0 1 4 5 6 7, esto se invierte a: 0 e 8 7 6 5, agregue tres = 2 3 8 9 t e.
01 4567 : 1er hexacordo P0/2do hexacordo I3 23 89te : 2do hexacordo P0/1er hexacordo I3escala cromática completa
La combinatoria retrógrada-inversional es una falta de tonos compartidos entre los hexacordios de una fila y su inversión retrógrada.
Babbitt también describió la fila semicombinatoria y la fila totalmente combinatoria, siendo esta última una fila que es combinatoria con cualquiera de sus derivaciones y sus transposiciones.Los conjuntos semicombinatorios son conjuntos cuyos hexacordos son capaces de formar un agregado con una de sus transformaciones básicas (R, I, RI) transpuesta. Existen trece hexacordos que son semicombinatorios solo por inversión.
(0) 0 1 2 3 4 6 // y 9 8 7 5(1) 0 1 2 3 5 7 // y 9 8 6 4(2) 0 1 2 3 6 7 // y 9 8 5 4(3) 0 1 2 4 5 8 // y 9 7 6 3(4) 0 1 2 4 6 8 // y 9 7 5 3(5) 0 1 2 5 7 8 // y 9 6 4 3(6) 0 1 3 4 6 9 // y 8 7 5 2(7) 0 1 3 5 7 9 // y 8 6 4 2(8) 0 1 3 5 8 9 // 7 6 4 2 y(9) 0 1 3 6 7 9 // y 8 5 4 2(10) 0 1 4 5 6 8 // 3 2 y 9 7(11) 0 2 3 4 6 8 // 1 y 9 7 5(12) 0 2 3 5 7 9 // 1 y 8 6 4
Todo hexacordo que contenga un cero en su vector de intervalo posee combinatoria transposicional (en otras palabras: para lograr la combinatoria, un hexacordo no puede ser transpuesto por un intervalo que sea igual a una nota que contiene). Por ejemplo, hay un hexacordo que es combinatorio por transposición (T6):
(0) 0 1 3 4 5 8 // 6 7 9 2
Ningún hexacordio contiene tritonos.


Los conjuntos combinatorios son conjuntos cuyos hexacordios son capaces de formar un agregado con cualquiera de sus transformaciones básicas transpuestas. Hay seis conjuntos fuente, o conjuntos combinatorios hexacordialmente básicos, cada uno de los cuales puede reordenarse dentro de sí mismo:
(A) 0 1 2 3 4 5 // 6 7 8 9 te(B) 0 2 3 4 5 7 // 6 8 9 y 1(C) 0 2 4 5 7 9 // 6 8 y 1 3(D) 0 1 2 6 7 8 // 3 4 5 9 te(E) 0 1 4 5 8 9 // 2 3 6 7 te(F) 0 2 4 6 8 t // 1 3 5 7 9 e
Nota: t = 10, e = 11.
Como los tres primeros conjuntos ( A , B y C ) satisfacen cada uno los cuatro criterios para un solo valor transposicional, el conjunto D los satisface para dos valores transposicionales, E para tres valores y F para seis transposiciones, Babbitt designa estos cuatro grupos como hexacordios combinatorios de "primer orden", "segundo orden", "tercer orden" y "sexto orden", respectivamente. [13] Nótese que el primer conjunto, el conjunto "A", son las primeras seis notas de una escala cromática ascendente, y que el último conjunto, el conjunto "F", es una escala de tonos enteros. [14]
La combinatoria puede utilizarse para crear un agregado de los doce tonos, aunque el término a menudo se refiere simplemente a filas combinatorias expresadas juntas.
La combinatoria hexacordal es un concepto de la teoría postonal que describe la combinación de hexacordios, que se utiliza a menudo en referencia a la música de la segunda escuela vienesa . En la música que utiliza de forma constante los doce tonos cromáticos (en particular, la música dodecafónica y serial ), el agregado (conjunto de las 12 clases de tonos) puede dividirse en dos hexacordios (conjuntos de 6 tonos). Esto divide el agregado en dos partes más pequeñas, lo que facilita la secuenciación de notas, el progreso entre filas o agregados y la combinación de notas y agregados.
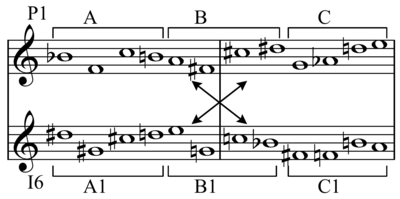
Ocasionalmente, un hexacordio puede combinarse con una versión invertida o transpuesta de sí mismo en un caso especial, lo que dará como resultado el agregado (conjunto completo de 12 tonos cromáticos).
Una fila (B ♭ =0: 0 6 8 5 7 e 4 3 9 t 1 2) utilizada por Schoenberg se puede dividir en dos hexacordios:
B ♭ EF ♯ E ♭ FA // DC ♯ GG ♯ BC
Al invertir el primer hexacordo y transponerlo, resulta el siguiente hexacordo, un reordenamiento del segundo hexacordo:
GC ♯ BDCG ♯ = DC ♯ GG ♯ BC
De esta manera, cuando se superpone el hexacordo original 1 (P0) sobre la inversión transpuesta del hexacordo 1 (I9 en este caso), se obtiene el conjunto completo de 12 tonos. Si se continúa con el resto de la fila transpuesta e invertida (I9) y se superpone el hexacordo original 2, se obtiene nuevamente el complemento completo de 12 tonos cromáticos.

La combinatoria hexacordal está estrechamente relacionada con la teoría de los 44 tropos creada por Josef Matthias Hauer en 1921, aunque parece que Hauer no tuvo ninguna influencia en Babbitt. Además, hay pocas pruebas que sugieran que Hauer tuviera un conocimiento extenso sobre las propiedades inversionales de los tropos antes de 1942 al menos. [17] Sin embargo, los primeros registros sobre las relaciones combinatorias de los hexacordios se pueden encontrar entre los escritos teóricos del compositor y teórico musical austríaco Othmar Steinbauer . [a] Realizó estudios elaborados sobre el sistema de tropos a principios de la década de 1930 que están documentados en un manuscrito inédito Klang- und Meloslehre (1932). Los materiales de Steinbauer fechados entre 1932 y 1934 contienen datos completos sobre tricords, tetracords y hexacords combinatorios, incluidos conjuntos semicombinatorios y totalmente combinatorios. Por lo tanto, pueden ser los registros más antiguos de la historia de la música. [18] Una compilación del material morfológico de Steinbauer se hizo pública en partes en 1960 con su guión Lehrbuch der Klangreihenkomposition (edición del autor) y se reimprimió en 2001. [19]
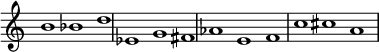
La combinatoria tricordal es la capacidad de una fila de formar agregados mediante la combinación de tricornos. "La combinatoria tricordal implica la presentación simultánea de cuatro filas en parcelas de tres piezas". [20] La existencia de combinatoria tricordal, o cualquier otra forma, en una fila no excluye la existencia de otras formas de combinatoria (al menos existe una combinatoria hexacordal trivial entre cada forma de fila y su retrógrada). Todas las filas derivadas tricordalmente poseen combinatoria tricordal.