Código convolucional

Tipo de código de corrección de errores que utiliza convolución

En telecomunicaciones , un código convolucional es un tipo de código de corrección de errores que genera símbolos de paridad mediante la aplicación deslizante de una función polinómica booleana a un flujo de datos. La aplicación deslizante representa la "convolución" del codificador sobre los datos, lo que da lugar al término "codificación convolucional". La naturaleza deslizante de los códigos convolucionales facilita la decodificación de enrejado mediante un enrejado invariante en el tiempo. La decodificación de enrejado invariante en el tiempo permite que los códigos convolucionales se decodifiquen mediante decisión suave de máxima verosimilitud con una complejidad razonable.

La capacidad de realizar una decodificación económica de decisión suave de máxima verosimilitud es uno de los principales beneficios de los códigos convolucionales. Esto contrasta con los códigos de bloque clásicos, que generalmente se representan mediante un enrejado variable en el tiempo y, por lo tanto, se decodifican típicamente mediante decisión dura. Los códigos convolucionales a menudo se caracterizan por la tasa de código base y la profundidad (o memoria) del codificador . La tasa de código base generalmente se da como , donde n es la tasa de datos de entrada sin procesar y k es la tasa de datos del flujo codificado del canal de salida. n es menor que k porque la codificación del canal inserta redundancia en los bits de entrada. La memoria a menudo se denomina "longitud de restricción" K , donde la salida es una función de la entrada actual y de las entradas anteriores. La profundidad también se puede dar como el número de elementos de memoria v en el polinomio o el número máximo posible de estados del codificador (normalmente: ). ${\displaystyle [n,k,K]}$ ${\displaystyle n/k}$ ${\displaystyle K-1}$ ${\displaystyle 2^{v}}$

Los códigos convolucionales suelen describirse como continuos. Sin embargo, también se puede decir que los códigos convolucionales tienen una longitud de bloque arbitraria, en lugar de ser continuos, ya que la mayor parte de la codificación convolucional del mundo real se realiza en bloques de datos. Los códigos de bloque codificados convolucionalmente suelen emplear terminación. La longitud de bloque arbitraria de los códigos convolucionales también se puede contrastar con los códigos de bloque clásicos , que generalmente tienen longitudes de bloque fijas que están determinadas por propiedades algebraicas.

La tasa de código de un código convolucional se modifica comúnmente mediante la perforación de símbolos . Por ejemplo, un código convolucional con una tasa de código "madre" se puede perforar a una tasa más alta, por ejemplo, simplemente al no transmitir una parte de los símbolos de código. El rendimiento de un código convolucional perforado generalmente se escala bien con la cantidad de paridad transmitida. La capacidad de realizar una decodificación de decisión suave económica en códigos convolucionales, así como la longitud de bloque y la flexibilidad de la tasa de código de los códigos convolucionales, los hace muy populares para las comunicaciones digitales. ${\displaystyle n/k=1/2}$ ${\displaystyle 7/8}$

Historia

Los códigos convolucionales fueron introducidos en 1955 por Peter Elias . Se pensaba que los códigos convolucionales podían ser decodificados con una calidad arbitraria a expensas del cálculo y el retraso. En 1967, Andrew Viterbi determinó que los códigos convolucionales podían ser decodificados con máxima verosimilitud con una complejidad razonable utilizando decodificadores basados ​​en enrejados invariantes en el tiempo: el algoritmo de Viterbi . Más tarde se desarrollaron otros algoritmos de decodificación basados ​​en enrejados, incluido el algoritmo de decodificación BCJR .

Los códigos convolucionales sistemáticos recursivos fueron inventados por Claude Berrou alrededor de 1991. Estos códigos resultaron especialmente útiles para el procesamiento iterativo, incluido el procesamiento de códigos concatenados como los códigos turbo . ^[1]

Usando la terminología "convolucional", un código convolucional clásico podría considerarse un filtro de respuesta de impulso finito (FIR), mientras que un código convolucional recursivo podría considerarse un filtro de respuesta de impulso infinito (IIR).

Dónde se utilizan códigos convolucionales

Etapas de codificación de canal en GSM. ^[2] Codificador de bloque y comprobación de paridad: parte de detección de errores. Codificador convolucional y decodificador de Viterbi: parte de corrección de errores. Entrelazado y desentrelazado: separación de palabras de código que aumenta en el dominio del tiempo y para evitar distorsiones por ráfagas.

Los códigos convolucionales se utilizan ampliamente para lograr una transferencia de datos confiable en numerosas aplicaciones, como video digital , radio, comunicaciones móviles (por ejemplo, en redes GSM, GPRS, EDGE y 3G (hasta 3GPP Release 7) ^{[3] [4]} ) y comunicaciones satelitales . ^[5] Estos códigos a menudo se implementan en concatenación con un código de decisión difícil, particularmente Reed–Solomon . Antes de los códigos turbo, tales construcciones eran las más eficientes y se acercaban más al límite de Shannon .

Codificación convolucional

Para codificar datos de forma convolucional, comience con k registros de memoria , cada uno con un bit de entrada. A menos que se especifique lo contrario, todos los registros de memoria comienzan con un valor de 0. El codificador tiene n sumadores módulo 2 (un sumador módulo 2 se puede implementar con una única compuerta XOR booleana , donde la lógica es: 0+0 = 0 , 0+1 = 1 , 1+0 = 1 , 1+1 = 0 ) y n polinomios generadores , uno para cada sumador (consulte la figura siguiente). Un bit de entrada m ₁ se alimenta al registro más a la izquierda. Usando los polinomios generadores y los valores existentes en los registros restantes, el codificador genera n símbolos. Estos símbolos se pueden transmitir o perforar según la tasa de código deseada. Ahora desplace bits todos los valores de registro hacia la derecha ( m ₁ se mueve a m ₀ , m ₀ se mueve a m ₋₁ ) y espere el siguiente bit de entrada. Si no quedan bits de entrada restantes, el codificador continúa desplazándose hasta que todos los registros hayan regresado al estado cero (terminación de bit de descarga).

Imagen 1. Codificador convolucional no recursivo y no sistemático de tasa 1/3 con longitud de restricción 3

La figura siguiente es un codificador de tasa 1 ⁄ 3 ( m ⁄ n ) con una longitud de restricción ( k ) de 3. Los polinomios generadores son G ₁ = (1,1,1), G ₂ = (0,1,1) , y G ₃ = (1,0,1) . Por lo tanto, los bits de salida se calculan (módulo 2) de la siguiente manera:

n1 = m1 + m0 ₊ m ₋ 1_​​

n2 = m0 ₊ m ₋ 1_​

n ₃ = m ₁ + m ₋₁ .

Los códigos convolucionales pueden ser sistemáticos y no sistemáticos:

• La repetición sistemática de la estructura del mensaje antes de codificarlo
• cambios no sistemáticos de la estructura inicial

Los códigos convolucionales no sistemáticos son más populares debido a su mejor inmunidad al ruido. Esto se relaciona con la distancia libre del código convolucional. ^[6]

• 
  Una breve ilustración de código convolucional no sistemático.
• 
  Una breve ilustración del código convolucional sistemático.

Códigos recursivos y no recursivos

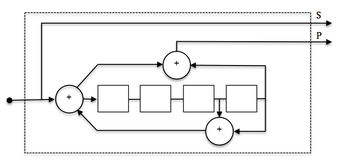
El codificador de la imagen de arriba es un codificador no recursivo . A continuación se muestra un ejemplo de uno recursivo y, como tal, admite una estructura de retroalimentación:

Img.2. Codificador convolucional sistemático recursivo de 8 estados con tasa 1/2. Se utiliza como código constituyente en el código Turbo 3GPP 25.212.

El codificador de ejemplo es sistemático porque los datos de entrada también se utilizan en los símbolos de salida (Salida 2). Los códigos con símbolos de salida que no incluyen los datos de entrada se denominan no sistemáticos.

Los códigos recursivos suelen ser sistemáticos y, a la inversa, los códigos no recursivos suelen ser no sistemáticos. No es un requisito estricto, pero sí una práctica habitual.

El codificador de ejemplo de la imagen 2 es un codificador de 8 estados porque los 3 registros crearán 8 estados posibles del codificador (2 ³ ). Un enrejado de decodificador correspondiente normalmente también utilizará 8 estados.

Los códigos convolucionales sistemáticos recursivos (RSC) se han vuelto más populares debido a su uso en códigos Turbo. Los códigos sistemáticos recursivos también se conocen como códigos pseudosistemáticos.

Otros códigos RSC y aplicaciones de ejemplo incluyen:

Img. 3. Código convolucional sistemático recursivo de dos estados (RSC). También llamado "acumulador".

Útil para la implementación de código LDPC y como código constituyente interno para códigos convolucionales concatenados en serie (SCCC).

Img. 4. Código convolucional sistemático recursivo (RSC) de cuatro estados.

Útil para SCCC y códigos turbo multidimensionales.

Img. 5. Código convolucional sistemático recursivo (RSC) de dieciséis estados.

Útil como código constituyente en códigos turbo con baja tasa de error para aplicaciones como enlaces satelitales. También es adecuado como código externo SCCC.

Respuesta al impulso, función de transferencia y longitud de restricción

Un codificador convolucional se llama así porque realiza una convolución del flujo de entrada con las respuestas de impulso del codificador :

${\displaystyle y_{i}^{j}=\sum _{k=0}^{\infty }h_{k}^{j}x_{i-k}=(x*h^{j})[i],}$

donde x es una secuencia de entrada, y ^j es una secuencia de la salida j , h ^j es una respuesta al impulso para la salida j y denota convolución. ${\displaystyle {*}}$

Un codificador convolucional es un sistema lineal discreto e invariante en el tiempo . Cada salida de un codificador se puede describir mediante su propia función de transferencia , que está estrechamente relacionada con el polinomio generador . Una respuesta al impulso está conectada con una función de transferencia a través de la transformada Z.

Las funciones de transferencia para el primer codificador (no recursivo) son:

• ${\displaystyle H_{1}(z)=1+z^{-1}+z^{-2},\,}$
• ${\displaystyle H_{2}(z)=z^{-1}+z^{-2},\,}$
• ${\displaystyle H_{3}(z)=1+z^{-2}.\,}$

Las funciones de transferencia para el segundo codificador (recursivo) son:

• ${\displaystyle H_{1}(z)={\frac {1+z^{-1}+z^{-3}}{1-z^{-2}-z^{-3}}},\,}$
• ${\displaystyle H_{2}(z)=1.\,}$

Definir m por

${\displaystyle m=\max _{i}\operatorname {polydeg} (H_{i}(1/z))\,}$

donde, para cualquier función racional , ${\displaystyle f(z)=P(z)/Q(z)\,}$

${\displaystyle \operatorname {polydeg} (f)=\max(\deg(P),\deg(Q))\,}$.

Entonces m es el máximo de los grados del polinomio

${\displaystyle H_{i}(1/z)\,}$, y la longitud de la restricción se define como . Por ejemplo, en el primer ejemplo la longitud de la restricción es 3 y en el segundo es 4. ${\displaystyle K=m+1\,}$

Diagrama de enrejado

Un codificador convolucional es una máquina de estados finitos . Un codificador con n celdas binarias tendrá 2 ⁿ estados.

Imaginemos que el codificador (que se muestra en la imagen 1, arriba) tiene '1' en la celda de memoria izquierda ( m ₀ ), y '0' en la derecha ( m ₋₁ ). ( m ₁ no es realmente una celda de memoria porque representa un valor actual). Designaremos dicho estado como "10". Según un bit de entrada, el codificador en el siguiente giro puede convertirse al estado "01" o al estado "11". Se puede ver que no todas las transiciones son posibles (por ejemplo, un decodificador no puede convertirse del estado "10" al "00" o incluso permanecer en el estado "10").

Todas las transiciones posibles se pueden mostrar a continuación:

Img.6. Diagrama de enrejado para el codificador de la Img.1. La ruta a través del enrejado se muestra como una línea roja. Las líneas continuas indican transiciones donde se ingresa un "0" y las líneas discontinuas donde se ingresa un "1".

En este gráfico, se puede representar una secuencia codificada real como una ruta. Se muestra una ruta válida en rojo como ejemplo.

Este diagrama nos da una idea sobre la decodificación : si una secuencia recibida no se ajusta a este gráfico, entonces se recibió con errores y debemos elegir la secuencia correcta más cercana (que se ajuste al gráfico). Los algoritmos de decodificación reales explotan esta idea.

Distancia libre y distribución de errores

Curvas de tasa de error de bits teóricas de QPSK codificado (decisión suave recursiva y no recursiva), canal de ruido blanco gaussiano aditivo. Las curvas son pequeñas y se distinguen debido a que las distancias libres y los pesos son aproximadamente los mismos.

La distancia libre ^[7] ( d ) es la distancia mínima de Hamming entre diferentes secuencias codificadas. La capacidad de corrección ( t ) de un código convolucional es el número de errores que puede corregir el código. Puede calcularse como

${\displaystyle t=\left\lfloor {\frac {d-1}{2}}\right\rfloor .}$

Dado que un código convolucional no utiliza bloques, sino que procesa un flujo de bits continuo, el valor de t se aplica a una cantidad de errores ubicados relativamente cerca unos de otros. Es decir, normalmente se pueden corregir varios grupos de t errores cuando están relativamente alejados entre sí.

La distancia libre puede interpretarse como la longitud mínima de una "ráfaga" errónea en la salida de un decodificador convolucional. El hecho de que los errores aparezcan como "ráfagas" debe tenerse en cuenta al diseñar un código concatenado con un código convolucional interno. La solución popular para este problema es intercalar los datos antes de la codificación convolucional, de modo que el código del bloque externo (generalmente Reed–Solomon ) pueda corregir la mayoría de los errores.

Descifrando códigos convolucionales

Curvas de tasa de errores de bits para códigos convolucionales con diferentes opciones de modulaciones digitales ( QPSK, 8-PSK , 16-QAM, 64-QAM ) y algoritmos LLR . ^{[8] [9]} (Exacta ^[10] y Aproximada ^[11] ) sobre canal de ruido blanco gaussiano aditivo.

Existen varios algoritmos para decodificar códigos convolucionales. Para valores relativamente pequeños de k , el algoritmo de Viterbi se utiliza universalmente, ya que proporciona un rendimiento de máxima verosimilitud y es altamente paralelizable. Por lo tanto, los decodificadores de Viterbi son fáciles de implementar en hardware VLSI y en software en CPU con conjuntos de instrucciones SIMD .

Los códigos de longitud de restricción más larga se decodifican de manera más práctica con cualquiera de los diversos algoritmos de decodificación secuencial , de los cuales el algoritmo Fano es el más conocido. A diferencia de la decodificación de Viterbi, la decodificación secuencial no es de máxima verosimilitud, pero su complejidad aumenta solo ligeramente con la longitud de restricción, lo que permite el uso de códigos fuertes de longitud de restricción larga. Dichos códigos se utilizaron en el programa Pioneer de principios de la década de 1970 para Júpiter y Saturno, pero dieron paso a códigos decodificados por Viterbi más cortos, generalmente concatenados con grandes códigos de corrección de errores Reed-Solomon que hacen más pronunciada la curva de tasa de error de bits general y producen tasas de error residual no detectado extremadamente bajas.

Tanto los algoritmos de decodificación secuencial como los de Viterbi devuelven decisiones difíciles: los bits que forman la palabra clave más probable. Se puede añadir una medida de confianza aproximada a cada bit mediante el uso del algoritmo de Viterbi de salida suave . Se pueden obtener decisiones suaves a posteriori máximas (MAP) para cada bit mediante el uso del algoritmo BCJR .

Códigos convolucionales populares

Registro de desplazamiento para el polinomio de código convolucional (7, [171, 133]). Ramas: , . Todas las operaciones matemáticas deben realizarse en módulo 2. ${\displaystyle h^{1}=171_{o}=[1111001]_{b}}$ ${\displaystyle h^{2}=133_{o}=[1011011]_{b}}$

Curvas de tasa de error de bits teóricas de QPSK codificado (decisión suave), canal de ruido blanco gaussiano aditivo. Las longitudes de restricción más largas producen códigos más potentes, pero la complejidad del algoritmo de Viterbi aumenta exponencialmente con las longitudes de restricción, lo que limita estos códigos más potentes a misiones en el espacio profundo donde el rendimiento adicional compensa fácilmente la mayor complejidad del decodificador.

De hecho, en la industria se utilizan estructuras de códigos convolucionales predefinidas obtenidas durante investigaciones científicas. Esto se relaciona con la posibilidad de seleccionar códigos convolucionales catastróficos (que provocan un mayor número de errores).

Un código convolucional decodificado por Viterbi especialmente popular, utilizado al menos desde el programa Voyager , tiene una longitud de restricción K de 7 y una tasa r de 1/2. ^[12]

Mars Pathfinder , Mars Exploration Rover y la sonda Cassini a Saturno utilizan un K de 15 y una tasa de 1/6; este código funciona aproximadamente 2 dB mejor que el código más simple a un costo de 256× en complejidad de decodificación (en comparación con los códigos de la misión Voyager). ${\displaystyle K=7}$

El código convolucional con una longitud de restricción de 2 y una tasa de 1/2 se utiliza en GSM como técnica de corrección de errores. ^[13]

Códigos convolucionales perforados

Códigos convolucionales con tasas de código de 1/2 y 3/4 (y longitud de restricción 7, decisión suave, 4-QAM / QPSK / OQPSK). ^[14]

Se puede diseñar un código convolucional con cualquier tasa de código basándose en la selección polinómica; ^[15] sin embargo, en la práctica, a menudo se utiliza un procedimiento de perforación para lograr la tasa de código requerida. La perforación es una técnica utilizada para crear un código de tasa m / n a partir de un código de tasa baja "básica" (por ejemplo, 1/ n ). Se logra eliminando algunos bits en la salida del codificador. Los bits se eliminan de acuerdo con una matriz de perforación . Las siguientes matrices de perforación son las más utilizadas:

Por ejemplo, si queremos generar un código con una tasa de 2/3 utilizando la matriz adecuada de la tabla anterior, debemos tomar la salida de un codificador básico y transmitir cada bit inicial de la primera rama y cada bit de la segunda. El orden específico de transmisión está definido por el estándar de comunicación respectivo.

Los códigos convolucionales perforados se utilizan ampliamente en las comunicaciones por satélite , por ejemplo, en los sistemas Intelsat y en la radiodifusión de vídeo digital .

Los códigos convolucionales perforados también se denominan "perforados".

Códigos turbo: reemplazando códigos convolucionales

Un código turbo con los códigos de componentes 13, 15. ^[16] Los códigos turbo reciben su nombre porque el decodificador utiliza retroalimentación, como un motor turbo. La permutación significa lo mismo que el entrelazado. C1 y C2 son códigos convolucionales recursivos. Los códigos convolucionales recursivos y no recursivos no son tan diferentes en el rendimiento de BER, sin embargo, el tipo recursivo se implementa en los códigos convolucionales Turbo debido a mejores propiedades de entrelazado. ^[17]

Los códigos convolucionales simples decodificados por Viterbi están dando paso a los códigos turbo , una nueva clase de códigos convolucionales cortos iterados que se acercan mucho a los límites teóricos impuestos por el teorema de Shannon con mucha menos complejidad de decodificación que el algoritmo de Viterbi en los códigos convolucionales largos que serían necesarios para el mismo rendimiento. La concatenación con un código algebraico externo (por ejemplo, Reed–Solomon ) aborda el problema de los niveles de error inherentes a los diseños de códigos turbo.

Véase también

• Código convolucional cuántico

Referencias

•  Este artículo incorpora material de dominio público de la Norma Federal 1037C. Administración de Servicios Generales . Archivado desde el original el 22 de enero de 2022.

1. Benedetto, Sergio y Guido Montorsi. "El papel de los códigos convolucionales recursivos en los códigos turbo". Electronics Letters 31.11 (1995): 858-859.
2. Eberspächer J. et al. Arquitectura, protocolos y servicios GSM. John Wiley & Sons, 2008. p. 97
3. Proyecto de asociación de tercera generación (septiembre de 2012). "3GGP TS45.001: Grupo de especificaciones técnicas de la red de acceso por radio GSM/EDGE; Capa física en la ruta de radio; Descripción general". Consultado el 20 de julio de 2013.
4. Halonen, Timo, Javier Romero y Juan Melero, eds. Rendimiento de GSM, GPRS y EDGE: evolución hacia 3G/UMTS. John Wiley & Sons, 2004. p. 430
5. Butman, SA, LJ Deutsch y RL Miller. "Rendimiento de códigos concatenados para misiones en el espacio profundo". The Telecommunications and Data Acquisition Progress Report 42-63, marzo-abril de 1981 (1981): 33-39.
6. Moon, Todd K. "Codificación de corrección de errores". Métodos matemáticos y algoritmos. Jhon Wiley and Son (2005). pág. 508
7. Moon, Todd K. "Codificación de corrección de errores". Métodos matemáticos y algoritmos. Jhon Wiley and Son (2005).- p.508
8. LLR frente a demodulación por decisión estricta (MathWorks)
9. Estimación de la BER para la decodificación de Viterbi de decisiones duras y blandas (MathWorks)
10. Modulación digital: Algoritmo LLR exacto (MathWorks)
11. Modulación digital: Algoritmo LLR aproximado (MathWorks)
12. Butman, SA, LJ Deutsch y RL Miller. "Rendimiento de códigos concatenados para misiones en el espacio profundo". The Telecommunications and Data Acquisition Progress Report 42-63, marzo-abril de 1981 (1981): 33-39.
13. Sistema global de comunicaciones móviles (GSM)
14. Codificación convolucional perforada (MathWorks)
15. "Convertir polinomios de código convolucional en descripción de celosía – MATLAB poly2trellis".
16. Código turbo
17. Benedetto, Sergio y Guido Montorsi. "El papel de los códigos convolucionales recursivos en los códigos turbo". Electronics Letters 31.11 (1995): 858-859.

Enlaces externos

• El libro de texto en línea: Teoría de la información, inferencia y algoritmos de aprendizaje, de David JC MacKay , analiza los códigos convolucionales en el Capítulo 48.
• Página de códigos de corrección de errores (ECC)
• Explicaciones de Matlab
• Fundamentos de los decodificadores convolucionales para mejorar las comunicaciones digitales
• Códigos convolucionales (MIT)
• Teoría de la información y codificación (TU Ilmenau) Archivado el 30 de agosto de 2017 en Wayback Machine , analiza los códigos convolucionales en la página 48.

Lectura adicional

Publicaciones

• Francis, Michael. "Decodificación de bloques del decodificador Viterbi: terminación enrejada y mordedura de cola". Xilinx XAPP551 v2. 0, DD (2005): 1-21.
• Chen, Qingchun, Wai Ho Mow y Pingzhi Fan. "Algunos resultados nuevos sobre códigos convolucionales recursivos y sus aplicaciones". Taller sobre teoría de la información, 2006. ITW'06 Chengdu. IEEE. IEEE, 2006.
• Fiebig, UC., y Patrick Robertson. "Decodificación por decisión suave y borrado en sistemas de saltos de frecuencia rápidos con códigos convolucionales, turbo y Reed-Solomon". IEEE Transactions on Communications 47.11 (1999): 1646-1654.
• Bhaskar, Vidhyacharan y Laurie L. Joiner. "Rendimiento de códigos convolucionales perforados en comunicaciones CDMA asíncronas en condiciones perfectas de seguimiento de fase". Computers & Electrical Engineering 30.8 (2004): 573-592.
• Modestino, J., y Shou Mui. "Rendimiento del código convolucional en el canal de desvanecimiento de Rician". IEEE Transactions on Communications 24.6 (1976): 592-606.
• Chen, Yuh-Long y Che-Ho Wei. "Evaluación del rendimiento de códigos convolucionales con MPSK en canales de desvanecimiento de Rician". Actas del IEE F-Communications, Radar and Signal Processing. Vol. 134. No. 2. IET, 1987.