¡Hola Mundo!
Mi interés en editar Wikipedia es la ilustración, así que déjame saber si deseas que se ilustre algún artículo sobre ciencia , tecnología , arquitectura o matemáticas . A continuación, se muestran algunos de mis trabajos hasta la fecha...
Después de un paseo en bote, les pregunté a mis invitados el clásico acertijo sobre los botes del Trinity College:
¿Qué concepto tienen todos los nombres en común?
(La respuesta está en Trinity College, Cambridge#Punt_names .)
De vuelta a casa, me sorprendió saber que no se mencionaba en el artículo , así que escribí una sección (por suerte, su nuevo barco, Charles , apareció en las noticias) y salí a hacer una sesión de fotos. Debí de tener un aspecto extraño al fotografiar solo los nombres a propósito.
Acertijo adicional: ¿Puedes decir cómo se relaciona cada nombre en la imagen con el concepto?
Como las imágenes híbridas me han cautivado durante años, me encantó encontrar una herramienta de inteligencia artificial que genera imágenes híbridas con una imagen inicial para la versión distante y un mensaje de texto para la versión cercana:
http://huggingface.co/spaces/AP123/IllusionDiffusion
Funciona mejor con caras reconocibles en alto contraste sobre un fondo simple.
Primero experimenté con imágenes famosas de Abraham Lincoln y el Che Guevara en escenas apropiadas antes de decidir que la Mona Lisa era la más relevante y reconocible a nivel internacional. También fue una suerte que la consigna "fotografía en color de una ciudad italiana en el Renacimiento" diera como resultado un paisaje ficticio estéticamente agradable. Para que el rostro se viera mejor, superpuse una copia tenue de la imagen de la semilla y retoqué manualmente los defectos.
Mi próximo paso podría ser encontrar un texto de Leonardo da Vinci , eliminar los espacios en blanco, reducir su tamaño y superponerlo en la imagen para crear tres niveles híbridos. ¿Alguna sugerencia sobre cómo crear cuatro niveles?
ACTUALIZACIÓN 24-09-2024: Hice una imagen híbrida con La joven de la perla de Vermeer .
Recientemente aprendí acerca de dos plantillas de tabla muy útiles:
Una limitación importante es que las tablas con varias filas de encabezado también deben tener activada la ordenación. Es una pena que no se puedan alinear los puntos decimales.
A modo de ejemplo, intente desplazarse por la página mientras observa la tabla de http://nssdc.gsfc.nasa.gov/planetary/factsheet a continuación.
Miserly-me quería introducir nuevos juegos a mi grupo de juegos de mesa, pero los juegos actuales son muy costosos.
Un amigo me contó sobre los juegos de imprimir y jugar (PnP) y se me ocurrió imprimirlos e insertarlos con naipes viejos en fundas para cartas de póquer de 64 mm × 89 mm.
Aunque Sprawlopolis y Air, Land and Sea fueron divertidos, Palm Island fue mi favorito. Como no había mucho texto en las tarjetas, pensé que podía hacer un PDF A4 de una versión isomórfica con fondos de dominio público (para evitar problemas de derechos de autor) para ilustrar Wikipedia. Lo llamé Balmy Isle .
En lugar de utilizar software de diseño como LibreOffice Draw , decidí codificar cada página en SVG para poder instanciar programáticamente partes repetidas para lograr coherencia.
Como tenía pensado imprimir cada página en papel normal e insertar una tarjeta entre la parte delantera y la trasera, hice que las dos filas superiores se doblaran. Es una pena que el diseño de 3x3 impidiera este tratamiento en las filas inferiores. Una versión A2 con tarjetas de 6x6 lo permitiría.
Aunque librsvg no reconoció algunos de los emojis utilizados, siempre que aparecieran en mi navegador, pude imprimir cada página en formato PDF. Como no pude encontrar una forma de crear varias páginas al imprimir, incorporé un interruptor para seleccionar qué página mostrar. Al fusionar y optimizar las copias digitales, obtuve el archivo cargado.
commons:user:Emreszer se puso en contacto conmigo para traducir mi mapa delta-v al turco y aproveché la oportunidad para agregar mapas de bits al diagrama.
Las fotografías de los objetos celestes que encontré tenían fondos negros, lo que me pareció desagradable a la vista contra el fondo blanco del gráfico, así que modifiqué la animación de rotación de los planetas para que no giraran, pero tuvieran el efecto esférico. También agregué otros objetos, restauré el aplanamiento que no se ve bien en la animación SVG, lo cargué en Firefox, tomé una captura de pantalla, la modifiqué hasta obtener un tamaño adecuado y la incrusté en el archivo SVG, que recorta cada objeto y lo coloca en el lugar apropiado.
Creo que esto hace que sea más fácil localizar los objetos y hace que el cartel sea atractivo, ¿no crees? 😊

En 2011, encontré artículos sobre puntos estacionarios , puntos de inflexión , etc. que carecían de diagramas que mostraran cómo se relacionaban entre sí los gráficos de las derivadas subsiguientes de una función cúbica. Para mi ilustración, quería una función cuyos puntos especiales tuvieran coordenadas enteras distintas y cuyos valores especiales no fueran cero.
Con la ayuda de Álvaro Lozano-Robledo, encontré una familia de funciones con la gráfica más "pequeña". Aun así, los valores de y son mucho mayores que los de x . Para conseguir una visualización razonable, tuve que hacer la escala vertical 50 veces mayor que la horizontal.
Fue un tema de discordia durante 12 años hasta que me di cuenta este año de que podía relajar una condición y también mostrar el efecto de una raíz repetida. Usando un script de Python , encontré una función "pequeña" que satisfacía mis objetivos: (también es interesante que las distintas raíces sean 1, 2, 3 y 4).
Para solucionar el error T97233 de rsvg, decidí utilizar caracteres Unicode prediseñados para las variables (en cursiva) y los superíndices. Al proporcionar la factorización de cada función, también se muestra cómo se derivan sus raíces.
Gracias también a GalacticShoe por un algoritmo para dibujar exactamente un segmento polinomial cúbico con una curva Bézier cúbica :
Si y los puntos finales son , , los puntos de control son
¿Alguien puede mejorar la función o presentación?

Me encontré con las magníficas fotografías de Penang tomadas con drones por HundenvonPenang y le pedí una foto del abandonado Penang Mutiara Beach Resort y de la recientemente inaugurada Gurney Bay . Me atendió y también me sugirió que nos reuniéramos porque estaba de visita en Penang.
*angys* se unió a la conversación y decidimos encontrarnos en Chap Goh Meh . Caminamos por George Town en un recorrido fotográfico de la procesión de Tua Pek Kong y el lanzamiento de naranjas en la Explanada. Fue maravilloso conocer a estos dos amables y diligentes wikipedistas.
También me pusieron en contacto con un grupo local encabezado por Ultron90 y ayudé a organizar su evento WikiGap hoy. Como el tema es sobre las mujeres en Malasia, decidí empezar un artículo sobre la eminente geógrafa y activista medioambiental Dra. Kam Suan Pheng . ¡Echa un vistazo a su artículo !

Me encontré con una idea ingeniosa de TilmannR para generar un SVG estático a partir de uno con JavaScript, lo que permite a los ilustradores crear diseños o gráficos demasiado complejos para crearlos manualmente. Si bien anteriormente había generado SVG con Python y Perl, una gran ventaja del método de TilmannR es que los editores solo necesitan un editor de texto y un navegador web para regenerar el SVG para subirlo a Commons, lo que no permite la ejecución de ningún script.
Le sugerí a TilmannR que incrustara el script como comentario en el SVG mismo, de modo que la fuente nunca se separara del archivo. Finalmente, se nos ocurrió reemplazar
que produce un SVG válido, pasa el filtro de Commons y, sin embargo, permite restaurar fácilmente el script eliminando "!--" y "--". Una desventaja es que el script no puede contener --(por suerte, esto se puede solucionar a menudo -= 1en JavaScript). El script vuelca en un grupo SVG con id GENERATED_CONTENTel contenido generado y en uno con id GENERATOR_SCRIPTel script comentado.
Mi primer intento, File:Gabriel_horn_2d.svg, fue un éxito. TilmannR lo revisó amablemente y recomendó las mejores prácticas de JavaScript.
Luego intenté rehacer el archivo File:Template_map_of_U.S._states_and_District_of_Columbia.svg , que depende de mi cuenta de Google para ejecutar una hoja de cálculo de Google Sheets. Después de consultar Timeshifter , trasladé sus funciones al archivo File:Template_map_of_US_states_and_District_of_Columbia.svg mencionado anteriormente. Si bien puede llevar un tiempo documentar su uso, espero haber comentado el código con suficiente claridad para que terceros generen su propio mapa coroplético de los estados de EE. UU. y Washington DC.
En las últimas horas de 2023, decidí implementar una idea que había visto en http://jsfiddle.net/elin/7m3bL hace años. Descubrí que su autor, Eddie Lin, había usado mucho las sombras de caja CSS y me pregunté si podía hacer algo similar con las rutas en SVG.
Hay dos series de fuegos artificiales funcionando simultáneamente, y se genera uno nuevo tan pronto como termina el anterior. Tener dos ofrece el mejor equilibrio entre rendimiento y hacer que la escena sea más animada.
Cada conjunto de fuegos artificiales tiene dos animaciones:
Para cada explosión, la escala simula las partículas en expansión mientras que la traducción simula la gravedad, haciendo que la facilidad se acelere a través de su ciclo. El color comienza con blanco puro para simular altas temperaturas, transformándose en el color deseado. stroke_width comienza en 9999, combinado con la escala creciente y el color blanco que simula el destello de cada explosión, y disminuye a cero para simular partículas en descomposición.
La posición salta a uno de los diez puntos (el centro más un cuadrado mágico de 3x3) al comienzo de cada explosión. dasharray determina el espaciado de las partículas a lo largo de las trayectorias dadas, simulando cierta aleatoriedad en el movimiento de las partículas. Para la última explosión de una secuencia, aumentar rápidamente el espaciado simula un efecto de "pez volador".
Cada camino constaba inicialmente de tres elipses que se entrecruzaban. En la última subida, me di cuenta de que podía preescalar los caminos para variar el tamaño de las partículas. Para variar, también reemplacé uno de los caminos con dos estrellas que se entrecruzaban a diferentes escalas.
¡Las subidas de Pity Commons no pueden tener sonido, por lo que tendrás que disfrutar del espectáculo en silencio!
Hasta el próximo post... Feliz año nuevo!
Pensé en probar suerte con la pintura digital y me compré una tableta gráfica XP-PEN en una oferta del Prime Day .
Mientras visitábamos un castillo, un amigo y yo observamos que la escalera helicoidal (de caracol) que conducía al sótano giraba de una manera poco convencional. Un "dato curioso" me recordó que este tipo de escaleras suelen girar de manera que el poste dificulta que los invasores, que suelen ser diestros, puedan blandir un arma. Me pregunté si esta escalera en particular era diferente porque la entrada estaba por encima de la habitación y, por lo tanto, los invasores tendrían que bajar.
Sin embargo, decidí dibujar la disposición típica después de descubrir que en Wikipedia no había una imagen de ese tipo. Lamentablemente, más tarde me enteré de que ese "dato" era un mito. Aun así, aprender a pintar en Krita fue una buena experiencia.

Hace muchos años, unos amigos y yo compartimos un huevo escocés en un picnic. Uno de nosotros se acordó del problema del sándwich de jamón y reflexionó sobre cómo cortarlo de modo que cada mitad tuviera la misma cantidad de clara, yema y masa. Pensamos equivocadamente que podíamos encontrar el plano que contenía el centro de gravedad de cada componente antes de darnos cuenta de que el centro de gravedad nos daría la media en lugar de la mediana, ya que la media pondera cada partícula según la distancia desde el centro de gravedad.
En casa, escribí un script en Python para ver cómo las líneas en diferentes ángulos dividían una forma bidimensional arbitraria en dos áreas iguales. Con OpenCV, leyó las imágenes como mapas de bits de 1 bit y contó la cantidad de píxeles negros.
Para cada ángulo, llené completamente de blanco un lado de la línea y conté los píxeles negros restantes. Al mover progresivamente la línea con la búsqueda binaria hasta que quedaran aproximadamente la mitad de los píxeles negros, obtuve la bisectriz de ese ángulo.
Al repetir esto cada 5 grados en distintas formas se obtuvieron lugares interesantes con un número impar de cúspides, incluso para formas con partes no contiguas.
Mucho más recientemente, pensé que el artículo sobre el teorema del sándwich de jamón podría funcionar con una ilustración en 2D, así que adapté el guión para que funcionara con dos colores. Elegí un mapa de las Islas Británicas porque estaba dividido convenientemente en dos países (principales), uno de los cuales tenía dos partes significativas.
La salida de Irlanda y el Reino Unido se colocó en los canales rojo, azul y verde, respectivamente, de modo que Irlanda apareciera en verde y el Reino Unido en rosa. La bisectriz común se destacó en negro.

Aunque conocía el conjunto de Cantor desde hacía muchos años, me intrigó su representación radial en http://gist.github.com/curran/74cb4d255acf072633a2df0d9b9be7c3 y traté de recrearla.
La primera fila de la versión lineal habitual se convierte en un círculo, en realidad un anillo con un radio interior cero, ya que abarca los 360°. Las filas siguientes se convierten en anillos rotos que crecen hacia afuera. Diferentes tonos de gris distinguen los anillos. El hecho de que cada anillo comience y termine en la parte inferior de la figura hace que parezca un pájaro estilizado.
El SVG fue generado por un script de Python que genera el conjunto de Cantor como una lista anidada y dibuja los anillos (excepto el más interno) usando stroke-dasharray, sus valores finales incrementados para evitar espacios debido al redondeo.
¿Crees que la figura sería un buen logotipo para una sociedad de matemáticas?
Chris25689 me recordó amablemente que actualizara mi diagrama de la Pirámide del Tiempo , ya que hoy ocurrió un evento que ocurre una vez cada década.
Hace diez años, ya había colocado el bloque 2023 en el SVG, pero lo comenté, por lo que creí que era una cuestión sencilla de descomentarlo. Desafortunadamente, el texto se desbordó, por lo que tuve que ajustar el viewBox . Bueno, valió la pena intentarlo...

Imaginemos que tenemos 4 frutas de cada tipo. Las vamos a colocar en un cuadrado de 4x4 de manera que cada fila y columna tenga exactamente una de cada una. Este tipo de cuadrado se denomina cuadrado latino . Podemos añadir el requisito de que las diagonales también tengan una de cada una. Para lograrlo, se debe reflejar un patrón diferente en ambas direcciones. Esto se denomina cuadrado latino con diagonales completas.
Podríamos sustituir cada fruta por un número. Como cada fila, columna y diagonal tiene un número de cada uno, la suma de cada uno es obviamente la misma.
Los cuadrados mágicos normalmente tienen números diferentes, pero hay una forma ingeniosa de convertir nuestro cuadrado latino en uno. Primero, sustituyamos la fruta por los números del 0 al 3. Podemos copiar el cuadrado con los números multiplicados por 4. Refleje el cuadrado en una diagonal y añádalo al primero. Al sumar uno, los números comienzan desde uno.

Podemos utilizar este método para hacer cuadrados mágicos similares a uno del famoso matemático Srinivasa Ramanujan , que tenía su cumpleaños, el 22 de diciembre de 1887, en la fila superior.
Al dividir una fecha, como lo hizo él, en día, mes, siglo y año, podemos sustituir el día menos uno, etc. Estos se eligen de modo que cuando se suman los cuadrados, la fila superior es simplemente el día, mes, siglo y año.
Ahora tenemos un método para generar un cuadrado mágico para cualquier fecha. Por supuesto, si, por ejemplo, el mes es enero o febrero, obtenemos valores negativos. Algunos números también pueden repetirse, pero, en caso contrario, el cuadrado tiene otras propiedades de cuadrado mágico.
Desafortunadamente, no podemos hacer cuadrados mágicos de fechas de 3 por 3 de esta manera, ya que solo hay un cuadrado latino de 3 por 3, ignorando la rotación y la reflexión, y una de sus diagonales tiene el mismo número repetido.
Hace diez años le planteé a @Timwi un problema práctico :
Lo resolvió en poco tiempo, hice el gráfico y pasamos a otras cosas.
Hace unos meses, @Pruthviraya afirmó que él o ella y sus hijas lograron que cada color tuviera exactamente 22 constelaciones, siendo 88 casualmente un múltiplo de cuatro. Sin embargo, descubrí que su sugerencia hace que dos regiones adyacentes tengan el mismo color, ya que la trama se envuelve alrededor de los lados.
Busqué a Timwi nuevamente con la nueva restricción y esta vez la resolvió con un programa en C♯ (detalles en commons:File_talk:constellations,_equirectangular_plot.svg). Después de actualizar el script de Perl, volví a generar el SVG anterior con este intérprete de Perl en línea que permite la entrada y salida de archivos.
Es maravilloso reencontrarse con viejos amigos y volver a tratar viejos y divertidos problemas. ¡Gracias, Timwi !

Dejando atrás POV-Ray , comencé a renderizar animaciones usando Blender 3.3.1 .
Su simulación física resultó muy útil para esta animación GIF de esférico rodante . De lo contrario, habría sido una tarea ardua configurar fotogramas clave para modelar el curioso movimiento rodante. Sin embargo, me decepcionó que la animación comience lentamente y se acelere con el tiempo. Tal vez debería haberla dejado funcionar hasta que alcanzara un estado estable antes de "grabar" la acción.
Para la animación de la paradoja de rotación de la moneda , intenté usar un mapeo normal para hacer que la iluminación fuera más realista, pero como el mapa de textura ya tenía una iluminación fuerte aplicada, el efecto no fue el esperado.
Un problema con el uso de Blender es que la fuente no es texto y .blendlos archivos no están permitidos en Commons. Por lo tanto, no pude cargar la fuente para que los editores futuros trabajaran en ella. Como solución alternativa, codifiqué el .blendarchivo con Base64 y lo cargué en una página de discusión. ¿Conoce una mejor solución?
Me cautivó un truco en Britain's Got Talent (temporada 14): el actor lo llamó "péndulo armónico" y lo encontré por su nombre habitual: "onda de péndulo". Me sorprendió encontrar la Wikipedia en inglés sin un artículo, así que me propuse crear uno.
La animación SVG con CSS es un medio ideal para ilustrar el movimiento, por lo que hice algunas versiones, incluida una con frecuencias en proporciones de números primos sugeridas por @Jpgordon : aunque demuestra una agrupación inesperada, el patrón no es tan sorprendente como el original .
Utilicé la idea de la línea de tiempo para visualizar espacialmente la agrupación en el original. Es fascinante cómo el orden surge del caos en determinados momentos:
Luego pensé en el truco que utilicé en Archivo:Comparison_satellite_navigation_orbits.svg para agregar un reloj a la animación para mostrar en qué parte del ciclo ocurre la agrupación.
En cuanto al código, la animación utiliza la misma técnica de transformación de fotogramas clave que suelo emplear en SVG animados, pero con movimientos suaves de entrada y salida y alternancia para imitar el movimiento. Aunque no se trata exactamente de un movimiento armónico simple , los movimientos suaves de entrada y salida modelan los péndulos lo suficientemente bien.
El siguiente paso es construir aparatos físicos con pateadores electromagnéticos para que los péndulos oscilen indefinidamente. Aunque no creo que haga el mío con balas de cañón en llamas 😅
Me encontré con este archivo de 15 MB en commons:Category:Large_SVG_files y pensé que podría optimizarse mucho más en tamaño, así que me comuniqué con Sarang , un experto en minimizar SVG que me enseñó a hackear stroke-dasharray .
Mrmw lo redujo a unos 22 KB mucho más razonables. Pensé que se podía reducir aún más, ya que eran solo una colección de 61 elipses. Al comprender su construcción, hice exactamente eso y lo reduje a 7 KB.
Luego decidí usar un truco que uso para aproximar elipses a cualquier precisión requerida usando el comando de ruta de arco , por ejemplo
<ruta d= "M 0,3 a 4,3 0 1 0 0.1,0" /> es casi equivalente a
<elipse cx= "0" cy= "0" rx= "4" ry= "3" /> 0,1 se puede reducir arbitrariamente para aumentar la precisión, pero debe ser distinto de cero.
Sin embargo, para este diagrama, la mayoría de las elipse están rotadas, por lo que tuve que usar el parámetro de rotación y calcular uno de los puntos extremos en dirección x o y (para lo cual una tangente a la elipse es vertical u horizontal).
Como había escrito el código Python para hacer todo eso, decidí iterar a través de diferentes desplazamientos x e y para el centroide y ajustar el viewBox en consecuencia para minimizar el tamaño del archivo SVG. Aunque podría haber usado el descenso de gradiente, el espacio de búsqueda era lo suficientemente pequeño como para forzar la solución.
Me complació reducir el tamaño del archivo a 1901 bytes, el 0,01% del original, en general un desafío divertido en Code Golf ⛳
El miniproyecto de este mes comenzó con el llamado de Timeshifter al Laboratorio de Gráficos (posteriormente trasladado ) para encontrar una forma sencilla de generar un mapa coroplético de los estados de EE. UU. y DC.
Shyamal y yo propusimos varios enfoques. Me decidí por crear un SVG editable por humanos, complementado con una hoja de cálculo de Google Docs.
El método aprovecha el manejo de la opacidad de los elementos de SVG para realizar una interpolación lineal del color de cada elemento:
Supongamos que se desea tener un color que se encuentre en un 40 % del camino entre el naranja (que indica el valor mínimo) y el cian (que indica el valor máximo). Se puede dibujar el elemento en naranja con una opacidad del 100 % y, luego, el elemento nuevamente en cian con una opacidad del 40 %. En caso de que falten datos para algunos estados, primero se puede dibujar todo el mapa en gris y omitir los dos elementos anteriores para los estados en los que falten datos.
Para que la edición sea lo más sencilla posible, agregué una hoja de estilos para cambiar fácilmente los colores y los elementos de texto de diversas etiquetas que se usarán en la lógica comercial, y estructuré las partes editables por el usuario de la siguiente manera:
<style type= "text/css" > <!-- Los colores mínimos, máximos y los datos no disponibles se detallan a continuación -->
.min { fill:#ff6600; } .max { relleno:#99ffff; }.n_a { fill:#cccccc; } </style> <g id= "overlay" > <!-- Valor relativo de 0,00 (mín.) a 1,00 (máx.) y las cadenas de texto se dan a continuación; reemplace el valor href con "#XXX" si los datos no están disponibles --> <use xlink:href= "#AL2" fill-opacity= "0,185" /><text id= "AL" > 7,25 </text> <use xlink:href= "#AK2" fill-opacity= "0,502" /><text id= "AK" > 10,85 </text> ... <use xlink:href= "#WY2" fill-opacity= "0.000" /><text id= "WY" > 5,15 </text> <text id= "legend_min" > 5,15 </text> <text id= "legend_max" > 16,50 </text> <text id= "title" > Salarios mínimos estatales , en dólares. 1 de enero de 2023 </text> Todo esto fue empaquetado como Archivo:Plantilla de mapa de los estados de EE. UU. y el Distrito de Columbia.svg con estadísticas de urbanización como ejemplo de caso de uso.
Lo que quedaba era generar las opacidades adecuadas. Para ello, decidí utilizar Google Docs, ya que las hojas de cálculo son más conocidas para los profanos que Python y se pueden compartir fácilmente en línea. Timesplitter podía pegar los datos en https://docs.google.com/spreadsheets/d/1qBwH0oA5IklYobs-igbVc0k-WsoxWPSbG0cgmGEZeys/edit y copiar y pegar el código generado en el archivo SVG en Notepad++.
Después de mucho ir y venir, el producto final es el que se muestra arriba. Es hora de pasar a otra cosa...
Conseguí una placa base clonada de Lego y muchas placas 1×1 del mismo color, y pensé en hacer un mosaico de Lego. Como el tamaño estaba limitado a 50×50 piezas (en realidad 48×48, para dejar un borde de 1 píxel), la resolución es extremadamente limitada. Peor aún, tener un solo color significaba solo un bit de color.
Partiendo de una resolución de 16×16 e inspirado por el usuario de DeviantArt Erminest-DA , logré hacer una representación decente del personaje de anime de la izquierda. Para agregar una historia a la obra de arte, agregué la cita inspiradora compuesta por palabras de solo 2 letras: "Si tiene que ser, depende de mí (hacerlo)". Decidí que la cursiva lo haría más dinámico. Pensar en una fuente con esta resolución fue un buen desafío. Por último, la adición de una espada y un dragón ilustró visualmente la cita.
ACTUALIZACIÓN 8 DE MARZO DE 2023: En este hilo, TilmannR presentó una forma de usar la interpolación del vecino más cercano: envolver una imagen (con tamaño en píxeles en lugar de thumb) de la siguiente manera:
<div style= "image-rendering:pixelated;" > [[Archivo:50x50x1b.png|100px]] </div> Hace tiempo que siento curiosidad por los rompecabezas de desaparición . Como Wikipedia no tiene ningún artículo al respecto, después de reunir suficiente material, decidí convertirlo en un miniproyecto para la semana de Navidad.
La naturaleza de estos rompecabezas me permitió usar el truco del mouse over que descubrí para hacer SVG interactivos , como en el ejemplo de El ciclista que desaparece.
Aunque sé cómo funciona, todavía no he encontrado una fuente fiable que lo explique. Si alguien tiene alguna referencia, por favor háganmelo saber .

PD: Algo relacionado, también encontré una manera de explicar de manera más sencilla el rompecabezas del cuadrado faltante :
¡Simplemente utilice proporciones de Fibonacci más pequeñas: 1:2 y 2:3 !
Me llevé una grata sorpresa al recibir un mensaje en el que me solicitaban una versión imprimible de mi infame tabla periódica de la nucleosíntesis.svg. El lector, que se hacía llamar Henk, aparentemente enseñaba física y quería un póster para colgar en su aula.
Honrado, decidí actualizar la descripción en commons:file:Nucleosynthesis_periodic_table.svg y formatearla bien debajo de la tabla periódica, también para hacer que la relación de aspecto sea más común para adaptarse a los tamaños de papel internacionales ISO 216 .
Para hacerlo, modifiqué el código SVG, lo abrí en Firefox, usé Imprimir > Microsoft Print to PDF y lo reduje con http://ilovepdf.com/compress_pdf usando "compresión extrema".
(Esto lo convierte en el segundo PDF que he subido a Commons, después de commons:file:Wikimania_2016_Dynamic_SVG_for_Wikimedia_projects.pdf – ¡en realidad una copia de seguridad de mi presentación de Wikimania 2016, en caso de que mi computadora portátil se estropee ! )

El mes pasado ocurrió algo curioso. Los aficionados a Among Us se enteraron de repente del diagrama con temática de parodia de Among Us que hice para ilustrar el teorema de Bayes , lo que dio lugar a una guerra de ediciones y una larga discusión .
De hecho, creo que el ejemplo de la probabilidad de que el personaje de un jugador sea un asesino dada su desconfianza es un uso magnífico y accesible del teorema, en comparación con las pruebas médicas.
El otro problema que se planteó fue que los íconos violaban los derechos de autor. No soy un experto en derechos de autor, pero al examinarlos en detalle con un miembro de la tripulación en el juego se observan diferencias intencionales. También evité cualquier terminología específica del juego.
Afortunadamente, el furor se calmó después de que la comunidad votó para mantener la imagen.

Hace muchos años, disfruté de un juego de simulación comercial llamado Taipan!. En un largo viaje en autobús desde Oxford, comencé a dibujar un mapa de estilo retro de sus puertos comerciales para su artículo.
Quería, en particular, bandas de tinte formadas por líneas paralelas y supuse que dibujando repetidamente las líneas de costa con un ancho de trazo decreciente en colores alternados lograría este efecto.
Luego se utilizaron efectos de filtro SVG para rellenar los mares con trazos horizontales cortos. Mientras jugaba con efectos de iluminación, encontré por casualidad una forma de simular líneas de contorno y relieve sombreado en la tierra.
Fue una lucha trabajar con las diferencias entre la representación de mi navegador y la de rsvg , pero el resultado general no se ve tan mal, ¿verdad ?
Encantado de que Cambridge tenga (aunque sea temporalmente) su propio modelo del Sistema Solar a escala 1:591 000 000 , actualicé mi sistema con SVG dinámicos incrustados.
Calculadora de modelos a escala del sistema solar
También subí posiblemente la escala más manejable, 1:10 000 000 000 como SVG independiente a Commons.
¡Esperamos que aparezcan más sistemas solares a gran escala en todo el mundo !

Después de dibujar con éxito el tablero de juego Risk como un gráfico con aristas rectilíneas y de 45°, decidí marcar el fin de la pandemia de COVID-19 con un nuevo dibujo del tablero de juego Pandemic .
Esta vez encontré draw.io, una aplicación web gratuita de dibujo vectorial que permite mover los vértices del gráfico mientras las aristas se mueven para adaptarse. No solo hizo que encontrar una disposición adecuada fuera mucho más eficiente, sino que el diagrama se podía exportar fácilmente, aunque lo redibujé con mi estilo preferido.
Desde que la vi por primera vez, la ilusión de Hollow-Face me fascinó. Primero hice un archivo STL que mostraba la ilusión, un buen ejercicio para aprender Blender . Conseguí encontrar un modelo CC-BY en Sketchfab y fue bastante fácil preparar las normales y reubicar el origen en Blender.
Luego, pensé que podía mejorar la animación GIF del artículo, así que continué con la creación de mi primera animación en Blender. En lugar de un archivo de video, decidí crear otro GIF, ya que tenía el problema de repetición con el reproductor de video en la sección siguiente.
Estoy muy satisfecho con el resultado. También hice uno que se mueve de izquierda a derecha para poder dedicarle más tiempo a la cara hueca. ¿Cuál prefieres?
¡Presentando mi primera contribución en video a Wiki[mp]edia !
Me sorprendió no encontrar ningún video del teorema de la raqueta de tenis en Wikimedia, así que decidí filmar tres demostraciones en mi patio trasero y hacer un video compuesto. Antes de filmar, cubrí con cinta la mitad de la raqueta para distinguir sus lados.
Después de extraer los fotogramas relevantes con FFmpeg , los recorté y los compuse con Python y OpenCV . Como la rotación ê 1 era mucho más rápida, repetí cada fotograma excepto el primero y el último. Invertí el orden de los fotogramas al final de la secuencia para que pudiera repetirse sin problemas. Finalmente, los exporté como video Ogg Theora con FFmpeg .
El vídeo se ve bien, aunque un poco borroso porque el enfoque automático de la cámara no logró enfocar la raqueta. También es un poco corto. Es una lástima que no haya podido encontrar una manera de hacer que el reproductor de vídeo reproduzca el clip en bucle. ¿Alguien tiene alguna idea?
ACTUALIZACIÓN 2022-05-04: Hice una animación GIF, Archivo:tennis_racket_theorem.gif que se ejecuta para siempre.
En cuanto a la hormiga sobre una cuerda de goma , se me ocurrió que las soluciones a los acertijos de cruce de ríos se pueden representar con líneas de tiempo . Son más útiles cuando se involucran unidades de tiempo, como el problema del puente y la antorcha y el acertijo de la cuerda quemada , pero también son beneficiosos cuando se muestran secuencias como en el problema de los misioneros y los caníbales y el problema del lobo, la cabra y el repollo .
El grupo Cambridge Wikimedian organizó una reunión en persona junto con Wikimania 2021. Pensé que sería apropiado realizar un recorrido fotográfico a pie por los monumentos catalogados cercanos después.
WikiShootMe identificó varias tumbas catalogadas en el cementerio de Mill Road . Aunque estaban cubiertas de vegetación, logré capturar la mayoría de ellas para Wikidata. También fue genial encontrarme con viejos compañeros de Wikidata después de un largo confinamiento por la pandemia.
Las listas de los países, islas y lagos más grandes a veces se ilustran con siluetas de cada objeto a escala. Si bien son útiles, se pierde el contexto porque faltan sus relaciones espaciales.
Me di cuenta de que la proyección Fuller o los mapas Dymaxion preservan sus posiciones relativas mientras mantienen aproximadamente la forma (conforme) y la escala (área igual), lo que permite comparar fácilmente las formas, tamaños y posiciones de estos objetos.
Después de encontrar mapas Dymaxion en blanco, creé estas tres visualizaciones. Lamentablemente, tuve que detener los diagramas de la isla y el país en el 30 para evitar que se llenaran demasiado, y el del lago en el 15, ya que el SVG original no tenía el lago Bangweulu.
En cuanto a SVG, no hay muchas novedades. Tuve que dividir algunas formas para obtener la parte relevante. El resto consiste simplemente en resaltar las formas adecuadas con CSS.
ACTUALIZACIÓN 2024-10-20: Estoy muy orgulloso de saber que el astronauta Chris Hadfield , mi héroe espacial, publicó sobre mi imagen 🥹
Después de crear el archivo File:Cambridge_University_colleges_timeline.svg , intenté crear uno para Oxford, pero no encontré suficiente información para llegar a ese punto. Me sorprendió gratamente que TSventon se pusiera en contacto conmigo y, a través de esta conversación , él o ella y Jonathan A Jones lograron descubrir suficientes datos para que el proyecto tuviera un nivel satisfactorio.


Me encontré con la magnífica habilidad de Sarang para reducir el tamaño de un archivo SVG a tan solo unos pocos cientos de bytes e intenté aplicar sus técnicas a algunos archivos SVG. El truco más impresionante es usar stroke-dasharray para dibujar líneas o formas repetidas, como esta figura, cuya fuente se encuentra a continuación:
<?xml version="1.0"?> <svg xmlns= "http://www.w3.org/2000/svg" viewBox= "0 0 8.05 8.05" fill= "ninguno" stroke= "#000" > <circle r= "99" fill= "#582" /> <path d= "M0,.5h7.5v1h-7v1h7v1h-7v1h7v1h-7v1h7v1h-7" stroke= "#feb" stroke-dasharray= "1" /> <path d= "M4,0v9M0,4h9" stroke-width= "9" stroke-dasharray= ".05,.95" /> <g stroke-width= ".5" stroke-dasharray= "0,2" stroke-linecap= "redondo" > <path d= "M1.5,.5h6v1h-7v1h8v3h-8m1,1h6v1h-7" ancho de trazo= ".6" /> <ruta d= "M1.5,.48h6v1h-7v1h7" trazo= "#c00" /> <ruta d= "M.5,5.48h7v1h-7v1h7" trazo= "#fff" /> </g> </svg> ¡Otro uso brillante de guiones SVG, además del tartán , las cadenas y los engranajes !

Alguien me preguntó en Template_talk:Generations_sidebar si podía simplificar mi imagen para que apareciera en Template:Generations_sidebar en tamaños pequeños. El SVG ya tenía internacionalización en catalán. En lugar de crear otra imagen, pensé en agregar otro "idioma" para ocultar detalles y hacer el texto más grande. lang=simple me pareció el "idioma" perfecto para este propósito. Para ocultar objetos, encontré que usar una etiqueta g en blanco era lo más sencillo:
< switch > < g systemLanguage = "simple" /> < use xlink : href = "#common_legend" /> </ switch > El cambio de tamaño de fuente se puede realizar mediante una clase CSS:
< switch > < text id = "gy-ca" transform = "translate(19720,-660)" dy = "0.7ex" systemLanguage = "ca" >< tspan class = "big" id = "trsvg27-ca" > Millennials ⧸ Generación Y </ tspan >< tspan x = "0" dy = "40" id = "trsvg28-ca" > ∗ 1981 – 96 </ tspan >/ text > < text id = "gy-simple" transform = "translate(19700,-660)" dy = "0.7ex" class = "simple" systemLanguage = "simple" >< tspan class = "big" id = "trsvg27" > Millennials </ tspan >< tspan x = "0" dy = "45" id = "trsvg28" > ∗ 1981 – 96 </ tspan ></ text > < text id = "gy" transform = "translate(19720,-660)" dy = "0.7ex" >< tspan class = "big" id = "trsvg27" > Millennials ⧸ Generación Y </ tspan >< tspan x = "0" dy = "40" id = "trsvg28" > ∗ 1981 – 96 </ tspan ></ text > </ switch > Una interacción reciente con David Eppstein me hizo interesarme en el daltonismo. La clasificación del daltonismo me enseñó que admitir la deuteranomalía, la protanomalía, la protanopía y la deuteranopía hace que mis diagramas sean accesibles para el 99,97 % de las personas con visión. Usando simulaciones de http://color-blindness.com/coblis-color-blindness-simulator, escribí un script de Python para crear una paleta de cuatro tonos (más gris) segura para la web que maximiza las diferencias para estos grupos y las personas con visión normal, y encontré el mejor compromiso
ACTUALIZACIÓN 19 DE SEPTIEMBRE DE 2021: Las pautas WCAG establecen 4,5 como la relación de contraste mínima para la clasificación AA para texto normal (o AAA para texto grande). Curiosamente, un color con una relación de alrededor de 4,6 con respecto al blanco también es de alrededor de 4,6 con respecto al negro. Por lo tanto, he encontrado 5 de esos colores que, en su mayoría, pueden distinguir las personas daltónicas y que se pueden representar con 3 dígitos hexadecimales:

Mientras depuraba un error de librsvg, aprendí sobre el uso de currentColor (sin distinción entre mayúsculas y minúsculas) para heredar colores en CSS.
Supongamos que tenemos algunos objetos de diferentes colores, pero el color de relleno de cada uno es el mismo que el color de su trazo , como en el caso de los puntos y las órbitas en este diagrama.
< style type = "text/css" > . toward { fill : #0000ff ; stroke : #0000ff ; } . forward { fill : #999999 ; stroke : #999999 ; } . orbit { fill : none ; } . object { stroke : none ; } </ style > < g class = "toward" > < use class = "orbit" xlink : href = "#orbit" /> < use class = "object" xlink : href = "#object" /> </ g > funciona pero repite los códigos de color, lo que posiblemente haga que se actualice una instancia pero no la otra. currentColor lo evita:
. hacia { color : #0000ff ; } . adelante { color : #999999 ; } . órbita { relleno : ninguno ; trazo : color actual ; } . objeto { relleno : color actual ; trazo : ninguno ; } En la parte superior del diagrama, un satélite en una órbita circular en el sentido de las agujas del reloj (punto amarillo) lanza objetos de masa insignificante:
Las elipses discontinuas son órbitas relativas a la Tierra. Las curvas continuas son perturbaciones relativas al satélite: en una órbita, (1) y (2) regresan al satélite después de haber realizado un bucle en el sentido de las agujas del reloj a cada lado del satélite. De manera poco intuitiva, (3) se aleja cada vez más en espiral hacia atrás, mientras que (4) se aleja en espiral hacia adelante.
SVG proporciona un útil filtro de mapa de desplazamiento que permite que una imagen sea "refractada" por otra. La escena submarina animada de la izquierda emplea la idea de [1] y [2], pero cambia el tono del mapa para evitar artefactos de ida y vuelta.
En lugar de animar un filtro, experimenté con la animación del objeto sobre el que se aplica un filtro que "convierte un cuadrado en un círculo", simulando una proyección ortográfica. Elegí nueve objetos astronómicos con texturas de commons:category:Solar_System_Scope. Cada textura se repitió y se desplazó horizontalmente a la velocidad correcta. Después de aplicar el filtro, calculado utilizando fórmulas de orthographic_map_projection#Mathematics , el resultado se recortó y se sombreó con una máscara, y se rotó a la inclinación axial correcta. Es una lástima que no pudiera imitar el aplanamiento, ya que Firefox generaba artefactos al intentar escalar imágenes filtradas.
Por último, con la ayuda de Wikipedia:SVG_help#Thumbnail_completely_black , agregué una textura sin distorsión que se oculta inmediatamente cuando comienza la animación, ya que el renderizador de miniaturas no reconoce feDisplacementMap.
La animación muestra que los gigantes gaseosos giran más rápido que los planetas terrestres, tanto que están sustancialmente aplanados. Venus, en el otro extremo, gira tan lentamente que tuve que conformarme con un compromiso de 10 000× de velocidad (y poner un marcador) para mostrar visiblemente el movimiento sin hacer que Júpiter y la Tierra giren demasiado rápido. También me parece interesante que Mercurio casi no tenga inclinación ni aplanamiento, pero su órbita está inclinada 7° respecto del plano de la eclíptica.
ACTUALIZACIÓN 20 DE JUNIO DE 2021: Al agregar la traducción al turco como lo solicitó Harald el Bardo , actualicé la clase dict2class en mi script generador de Python para trabajar de forma recursiva con diccionarios anidados :
clase dict2class ( dict ): def __getattr__ ( self , k ): devuelve dict2class ( self [ k ]) si esinstancia ( self [ k ], dict ) de lo contrario self [ k ]
La serendipia me llevó a este atractivo mapa 3D y me complació ver que su autor, Tom Patterson, lo había compartido generosamente junto con otros magníficos mapas de dominio público.
Subí sus tres versiones a Commons y nominé la versión en inglés como imagen destacada . Me alegra que varios otros editores y administradores hayan estado de acuerdo, y ahora es el mapa destacado más reciente .
Le envié un correo electrónico para felicitar al Sr. Patterson y le pregunté si podría estar interesado en hacer una en Challenger Deep o en la región de Tharsis . ¡Cruzo los dedos !

En los primeros días de la Web, a los desarrolladores web les encantaba usar imágenes de orbes vidriosos como viñetas en listas desordenadas. Un estilo que me gustaba era el efecto de orbe translúcido brillante de Apple , que se podía recrear usando dos degradados y un filtro (sin los cuales el "reflejo" es más nítido):
<filter id= "filter_blur" ><feGaussianBlur stdDeviation= "4" /></filter> <radialGradient id= "grad_sphere" cx= "50%" cy= "50%" r= "50%" fx= "50%" fy= "90%" > <stop offset= "0%" stop-color= "#000000" stop-opacity= "0" /> <stop offset= "99%" stop-color= "#000000" stop-opacity= "0.3" /> </radialGradient> <linearGradient id= "grad_highlight" x1= "0%" y1= "0%" x2= "0%" y2= "100%" > <stop offset= "10%" stop-color= "#ffffff" stop-opacity= "0.9" /> <stop offset= "99%" stop-color= "#ffffff" stop-opacity= "0" /> </linearGradient> <g id= "orbe" stroke= "ninguno" > <circle cx= "0" cy= "0" r= "100" /> <circle cx= "0" cy= "0" r= "100" fill= "url(#grad_sphere)" /> <ellipse cx= "0" cy= "-45" rx= "70" ry= "50" fill= "url(#grad_highlight)" filter= "url(#filter_blur)" /> </g> Como desde entonces he hecho varios diagramas con este efecto, decidí ponerlos en el orbe commons:category:SVG, análogo a commons:category:4-3-2_trimetric_projection.
El post de este mes trata sobre chistes y coincidencias matemáticas .
Curiosamente, 40.000 km (25.000 mi) aparece repetidamente en las estadísticas sobre la Tierra :
El radio de la órbita geoestacionaria , 42.164 kilómetros (26.199 millas), se encuentra dentro del 0,02% de la variación de la distancia de la Luna en un mes (la diferencia entre su apogeo y perigeo), 42.171 kilómetros (26.204 millas), y el 5% de error de la longitud del ecuador , 40.075 kilómetros (24.901 millas). De manera similar, la velocidad de escape de la Tierra es 40.270 km/h (25.020 mph).
Por otra parte, encuentro divertidos algunos razonamientos falaces, como la cancelación anómala antes mencionada que triunfa .
También resulta divertida esta verdadera observación:

Tuve la tentación de hacer que la densidad sea η – ordenando eta , la masa se convierte en comer pizza . Además, su peso es pizzagate – ¡aunque esta referencia podría quedar obsoleta muy pronto !
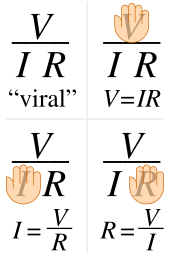
Me acordé de los "triángulos de fórmulas" que ideé para recordar fórmulas simples en la escuela y descubrí que en Wikipedia no había un diagrama que mostrara su uso, así que dibujé esto. Aunque es más conocido por la ley de Ohm, se puede aplicar a cualquier fórmula en la forma a = b · c · d · … (cada parámetro puede ser una función, pero se debe tomar la inversa del resto). Por lo tanto, dibujé un diagrama para estudiantes de física de secundaria a continuación. La selección exacta depende del programa de estudios, pero creo que he cubierto los más comunes.
En cuanto a los mnemónicos, hace poco descubrí uno para recordar el orden de los colores (ya sé que es Roy G Biv , pero ¿ en qué dirección?) en los espectros de refracción y difracción: R efracción reducida . Me costó encontrar un equivalente para difracción hasta que me di cuenta de lo siguiente: ¡ La difracción es diferente !
Parece que en el caso de los arcoíris ocurre lo contrario: se podría esperar que el rojo estuviera en el interior, pero hay un reflejo en las gotas de lluvia para los arcoíris primarios y dos para los secundarios . Un mnemónico adecuado es ¡R i m e r o d e arcoíris rojo !
Acabo de encontrar una forma de mejorar aún más los SVG como ayudas didácticas resaltando dos partes diferentes de un diagrama para compararlas usando solo CSS (SMIL permite resaltar cualquier cantidad de partes, pero el código es más difícil de manejar y había planes para desaprobar SMIL). En este gráfico de ejemplo, supongamos que un tutor desea señalar que la función vercosina es simplemente la función coseno más uno. En un dispositivo habilitado para mouse, puede hacer clic en el gráfico cos para resaltarlo (los demás gráficos se desvanecen) y luego pasar el mouse sobre el gráfico vercosina para que desaparezca y se coloque un brillo amarillo a su alrededor.
Mi método hackea los hipervínculos al vincularlos al mismo archivo mediante un ancla en blanco ( # ). Cuando se hace clic en un vínculo, su estado pasa a ser foco (en lugar de pasar el mouse sobre él cuando se pasa el mouse sobre él). A continuación se muestra la hoja de estilo: outline:none; oculta el contorno de un vínculo enfocado. Como antes, el brillo se logra con un filtro:
<style type= "text/css" >
.main:hover { opacidad de relleno: 0,2; opacidad de trazo: 0,2; } .active:hover { opacidad de relleno:1; opacidad de trazo:1; filtro:url(#filter_glow); }.active:focus { opacidad de relleno:1; opacidad de trazo:1; contorno:ninguno; }.nofade { opacidad de relleno: 1; opacidad de trazo: 1; } </style> <filter id= "filter_glow" > <feGaussianBlur en= "SourceAlpha" stdDeviation= "2" /> <feColorMatrix en= "blur" tipo= "matrix" valores= "0,0,0,0,1 0,0,0,0,1 0,0,0,0,0 0,0,0,2,0" /> <feBlend en= "SourceGraphic" /> </filter> Finalmente cada parte interactiva se define de la siguiente manera:
<a class="activo" xlink:href="#"> ... </a> Otro uso podría ser la revelación de información en varias etapas. Por ejemplo, un rompecabezas puede mostrar una pista al pasar el cursor sobre él y una respuesta al hacer clic. Me pregunto qué otros usos existen para este mecanismo...
Anteriormente había creado una serie de animaciones GIF visualizando series de Fourier y quería convertirlas en animaciones SVG, pero no sabía cómo hacer objetos animados anidados suaves; mi archivo:Rolling_circle_optical_illusion.svg era bastante desigual.
Cuando me encontré con la paradoja de la rotación de la moneda , le di otra oportunidad. Contiene dos animaciones: un círculo que rueda a lo largo de una línea y otra alrededor de otro círculo. Descubrí que anidar transformaciones sin ninguna otra transformación entre ellas funcionaba bien:
<g clase= "movimiento2" > <uso clase= "rot1" xlink:href= "#r" /> </g> ...<g clase= "rot2" > <g transformación= "traducir(0,-944)" > <uso clase= "rot1" xlink:href= "#r" /> </g> </g> donde move2 , rot1 y rot2 son animaciones CSS y r es el círculo a animar.
Tras el éxito, decidí abordar el problema de la transformada de Fourier. La parte más difícil fue sincronizar las animaciones. A diferencia de la animación en, por ejemplo, JavaScript, en la que se pueden especificar las rotaciones y traslaciones de cada fotograma, la animación CSS requiere especificar el período de cada animación. Los errores de redondeo se acumulan, por ejemplo, si el círculo A tiene un período de 1 s y el B de 0,33 s, mientras que inicialmente A parece girar 3 veces más rápido que B, después de 300 rotaciones, B se retrasará una rotación. Una solución que encontré fue hacer que todos los períodos sean fracciones de su mínimo común múltiplo . Los multiplicadores θ son 1, 3, 5 y 7. Además, para la figura combinada, necesitaba otro período para restar la rotación del círculo verde del círculo amarillo, etc., por lo tanto, un multiplicador efectivo de 2. Al ser coprimos, su MCM es 2 × 1 × 3 × 5 × 7 = 210. Por lo tanto, elegí 21 s para el círculo amarillo, lo que da 7 s, 4,2 s y 3 s para los otros círculos, y 10,5 s para la diferencia. (Sé que los quintos, por ejemplo, 4,2, no se pueden definir exactamente en binario (como 1/3 no puede estar en decimal), pero creo que el error es insignificante). ¡Después de mucho ensayo y error, funcionó !
ACTUALIZACIÓN 1 JUL 2020: Hice esta animación de engranajes planetarios...
ACTUALIZACIÓN 26 JUL 2020: ...y esta animación de funciones trigonométricas en un círculo unitario.

En 2012, dibujé el diagrama de la izquierda para ilustrar la interpolación lineal. Creo que hace que la fórmula quede mucho más clara. Durante ocho años, he buscado un equivalente para la interpolación cúbica. Después de consultar en la mesa de referencia de matemáticas y leer sobre el polinomio de Lagrange y el spline cúbico de Hermite , creo que finalmente lo encontré.
Aprendí que la interpolación cúbica no es única, ya que existe un grado de libertad sin restricciones: la interpolación polinómica analiza varios enfoques. Uno que me pareció adecuado para visualizar es el Catmull-Rom, que pasa por los cuatro puntos de control y, por lo tanto, se puede expresar utilizando polinomios de base de Lagrange. ¡Ese es un algoritmo que usaré en mi trabajo diario !

Una discusión sobre impresión 3D reavivó mi interés de siempre por los recorridos de Euler : cómo dibujar una trayectoria con un trazo continuo sin doblez. Muchos saben que la clave es tener dos o menos vértices con aristas impares.
En 2015, descubrí que los artículos sobre el camino euleriano , los siete puentes de Königsberg y el rompecabezas de las cinco habitaciones carecían de diagramas que mostraran realmente el recuento de aristas, así que dibujé este diagrama. Después de dibujar File:Eulerian_path_puzzles.svg , lo revisé y pensé que las aristas del vértice "9" estaban desordenadas. En ese momento, no podía decir qué era objetable. Me acabo de dar cuenta de que probablemente se trataba de los espacios entre las rutas que no aumentaban o disminuían monótonamente. Los volví a dibujar como a la derecha, haciendo que comenzaran casi paralelos y luego divergieran.
Un beneficio adicional es que parece un pequeño mamífero como un gato o un zorro, con orejas y bigotes 🐱

Me uní a una discusión en Commons_talk:SVG_Translate_tool sobre la herramienta SVG Translate. Ayudé a User:Ikonact a depurar por qué la herramienta no mostraba ninguna cadena para traducir en File:Corsica-geographic_map-en.svg y descubrí que tener una hoja de estilo con un selector de ID style (aquellos que comienzan con #) hace que la herramienta falle. Lo reporté como un error grave, ya que muchos SVG los usan. Para solucionar el problema, decidí cambiar id="main"a class="main"en mis nuevos.
Otro problema con la herramienta es que no actualiza la memoria caché de archivos, por lo que si se carga una nueva versión de un archivo, no la ve hasta varias horas después, lo que hace que sea muy difícil hacer algo . Recurrí a numerar secuencialmente las cargas, colocándolas bajo una categoría y solicitando que se eliminen y pidiendo a un administrador que las elimine.
Una de las cosas que más me resultó útil de la actividad fue aprender sobre el verificador SVG de Commons. Es muy útil poder ver la miniatura renderizada y descubrir errores SVG antes de subirla. Un truco es usarlo para renderizar un archivo PNG a partir de un SVG sin subirlo. Sé que puedo descargar herramientas para hacerlo, pero esto funciona desde cualquier computadora sin instalar nada .
Tuve una breve colaboración con @Juandamec: y @ Kirill Borisenko : sobre mi infografía de la línea de tiempo de las Siete Maravillas del Mundo Antiguo después de que amablemente la tradujeron al español y al ruso, respectivamente.
Al decidir convertirlo en un SVG multilingüe, no encontré una forma sencilla de ver los idiomas no predeterminados en un navegador antes de cargarlos. Una forma de hacerlo es instalar y cambiar el idioma del navegador y reiniciarlo, pero eso es un fastidio y afecta a toda la interfaz del navegador.
Por lo tanto, escribí un script en Python3 para extraer y escribir un archivo SVG monolingüe a partir de un archivo SVG multilingüe. Como no podía cargar un archivo Python, copié su código fuente en user:cmglee/extract_lang.py para que cualquiera pudiera copiarlo y pegarlo.
Mi primer uso fue para hackear la función multilingüe para crear un SVG que muestre los pasos para hacer un gráfico ternario , como el anterior. Lo bueno de esta técnica es que los editores pueden actualizar elementos comunes, por ejemplo, la cuadrícula y los ejes en un archivo en lugar de varios. Lamentablemente, la elección de códigos de idioma es limitada, por lo que elegí aa , ba , ca y da para hacer una secuencia razonable.
Acabo de descubrir (creo) una nueva aplicación para SVG interactivo sin JavaScript: un cuestionario que permite a los estudiantes aprender la ubicación de características geográficas, componentes de un sistema, etc. (básicamente, cualquier mapeo 1 a 1). Mi primer ejemplo se refiere a los estados de los EE. UU.
Me pregunto si alguien aquí conoce una forma elegante de implementar contadores sin JavaScript . En mi ejemplo, un estudiante podría comenzar con, digamos, tres vidas. Cada respuesta incorrecta (activada por el elemento "reset") descuenta una vida. Cuando se pierden todas las vidas, el juego termina. Una solución alternativa es tener tantos elementos de reinicio como vidas y eliminar los elementos a medida que se agotan las vidas. Sin embargo, eso generaría mucho código redundante :-(
Una versión menos estricta sólo cuenta el número de respuestas incorrectas y lo muestra al final cuando se han identificado todos los estados.
Como alternativa, podría implementar un temporizador que cuente la cantidad de segundos (como en mi demostración de transformación) pero que lo pause cuando se hayan identificado todos los estados, para mostrar cuánto tiempo le tomó al estudiante. Una solución alternativa es agregar onmousemove="document.getElementsByTagName('svg')[0].pauseAnimations();"la pantalla de victoria, pero:
on*atributos(Puedo hacer una versión en la que un cronómetro cuenta regresivamente hasta cero y el juego termina si el estudiante no logra identificar todos los estados a tiempo, como en mi juego de misiles, aunque un límite de tiempo puede frustrar a los estudiantes).
¿Podrías ayudarme?
Una de las ventajas de los vuelos es ver y fotografiar vistas aéreas. Un consejo que he encontrado es disparar lo más perpendicularmente posible a la ventana y evitar el turbulento escape. Para eliminar la neblina, utiliza la máscara rápida de GIMP para crear una selección de degradado de cerca a lejos y utiliza la herramienta Curvas para fijar los canales de color, especialmente el azul, y ajustar el brillo y el contraste. Reducir la saturación del color disminuye el tono amarillento de las nubes. Sin embargo, cuando el aire está despejado, los resultados son espectaculares.
El usuario:Drégigori me informó que el objeto transneptuniano Ultima Thule había sido renombrado Arrokoth. Mientras revisaba la actualización del usuario:Mrmw a file:interstellar_probes_trajectory.svg , pensé que al pasar el cursor sobre una sonda interestelar se deberían resaltar todos los objetos astronómicos con los que interactuaba, y viceversa. Al clasificar el objeto sobre el que se pasaba el cursor como activo y sus objetos asociados como asociados , me di cuenta de que cada grupo activo podría contener copias de los objetos asociados con pointer-events:none establecido, por ejemplo
<style type= "text/css" > #main:hover { opacidad de trazo: 0,05; opacidad de relleno: 0,05; } .nofade, .active:hover { opacidad de trazo: 1; opacidad de relleno: 1; } .nofade, .associated { eventos de puntero: ninguno; } ... </style> ...<g class= "activo" > <g class= "asociado" > <use xlink:href= "#p1" /> <!-- Pioneer 11 --> <use xlink:href= "#v1" /> <!-- Voyager 1 --> <use xlink:href= "#v2" /> <!-- Voyager 2 --> </g> <use xlink:href= "#s" /> <!-- Saturno --> </g> ...Hice este ejemplo de juguete para que los editores puedan reutilizar esta técnica y actualicé el archivo:interstellar_probes_trajectory.svg en consecuencia.

Este año, las autoridades del Scrabble inglés agregaron tres palabras de dos letras a la lista de palabras válidas :¡Qué extraño!,DE ACUERDOyZE– lo cual leí como "EL EWOK!" Para marcar la ocasión, hice esta tabla que muestra todas las palabras válidas de dos letras que comienzan y terminan con cada letra, anotando años de cambios (es una maravillaFilipinasentró).
Lamentablemente, todavía no hay ninguno conV☹ – Si alguno de ustedes alguna vez se vuelve famoso e inventa alguna tecnología o concepto que involucre visión, por favor, por favor, por favor, llámenlo unaVI☺
Commons:User:Cwtyler me envió un mensaje sobre una ilusión óptica de deriva periférica que hice hace cinco años; descubrió que los colores se desvanecen después de mirarla.
Curiosamente, la miniatura de Wikimedia no muestra lo que yo había pensado originalmente: debería haber parecido a la versión corregida que aparece a continuación. Cuando tuve problemas con un degradado lineal SVG que se transformaba incorrectamente para mi diagrama de sistemas de aterrizaje que aparece a continuación, User:Glrx me enseñó a agregarlo gradientUnits="userSpaceOnUse"para que librsvg coincida con los navegadores web modernos. El inconveniente es que los valores x e y no se pueden especificar en porcentajes.
Después de arreglar la miniatura, decidí generar una ilusión de desplazamiento periférico muy fuerte. Descubrí que el color es irrelevante: solo lo es la luminancia. Sorprendentemente, descubrí que si lo giro (por ejemplo, en mi teléfono) 45° en cualquier dirección, ¡el desplazamiento se detiene ! ¿Alguien puede explicar por qué?
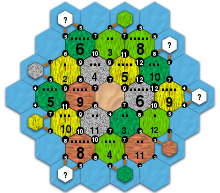

Continuando mi experimentación con filtros SVG, disfruté haciendo texturas para los tipos de terreno de Catan con feTurbulence :
Lamentablemente, la intensidad de la textura en Firefox y Chrome no coincide con la de la miniatura de Wikimedia (librsvg), las texturas con efectos de iluminación se atenúan y viceversa. Sin embargo, el gráfico muestra el mapa inicial de Catan Universe , siendo el punto principal la probabilidad relativa de que cada ubicación de asentamiento produzca productos. Parece un poco desequilibrado, la esquina noreste tiene varios 12 y el único puerto genérico está bordeado por dos hexágonos de terreno.
ACTUALIZACIÓN 17 NOV 2019: Un uso más real de las texturas SVG se encuentra en el archivo:Brooklyn_bridge_section.svg .

¡Saludos desde Estocolmo Wikimania 2019 !
Anteriormente me había esforzado por recordar a qué rotaciones se referían los lanzamientos de balanceo, cabeceo y guiñada , y me encontré con una regla mnemotécnica de un lanzador de béisbol haciendo un lanzamiento por encima de la cabeza . Como los lanzamientos de costado son más bien de guiñada, pensé en un lanzador de agua: ¡solo una rotación sensata evita derramar agua por todas partes ! A continuación, el balanceo es inequívoco cuando se aplica a un perro o un gato.
Por último, está yaw. Lamentablemente, un bostezo, o asentir con la cabeza para indicar que "sí", es más parecido a un tono. Entonces busqué palabras que rimaran con "yaw". "Draw" describe el movimiento del antebrazo de un artista. Pero la más clara es "door" (que rima en inglés británico, sin la "r" pronunciada: /dɔː/) –no la variedad garage, por supuesto. De ahí el dibujo...
No hay nada especial en el lado SVG, excepto tal vez el uso de transformaciones de escala y rotación , y el apilamiento de formas para hacer la flecha pseudo-3D.

Al actualizar este gráfico, pensé en sombrear los espacios entre los gráficos de los equipos que compiten para mostrar quién va en cabeza en cada momento, pero no se me ocurrió una forma elegante en SVG. Este año, se me ocurrió usar dos rutas de recorte : Al aplicar una ruta de recorte que selecciona la región por encima del gráfico A a la región por debajo del gráfico B, solo quedan las regiones por encima de A pero por debajo de B, y viceversa. La figura de la derecha explica los pasos visualmente. Para evitar superponer regiones, decidí hacerlo solo para los Blue Boats.
Para complementar las fechas que se muestran al pasar el cursor sobre un gráfico o la leyenda, hice que al pasar el cursor sobre una región en blanco se muestren los resultados del año más cercano. Me pregunto cómo puedo llamar la atención sobre el empate técnico en 1877...
Ian Furst me contactó para pedirme ayuda con un video en el que está trabajando . Quería una plantilla que mostrara el contorno de un cuerpo humano con varios síntomas superpuestos en las partes relevantes. Los editores pueden especificar fácilmente la combinación de síntomas que se muestran mediante Wikitext.
Después de pensarlo un poco, decidí crear una plantilla que envolviera template:Location mark+ . También aprendí sobre el uso de
{{#invoke:String|find|haystack|needle}}
Para comprobar si una cadena contiene otra. Se puede especificar cualquier combinación de los síntomas admitidos de la siguiente manera:
{{User:Cmglee/T symptoms man|Bieberitis|nausea,shortness_of_breath,tingling,muscle_weakness}}
Hubiera sido mucho mejor si SVG admitiera la capacidad de habilitar y deshabilitar sus partes sin JavaScript. Anteriormente, descubrí la capacidad de hackear la funcionalidad systemLanguage, pero con solo 443 idiomas admitidos, la libertad total para admitir las 2 n combinaciones permite solo n = 8 síntomas, a pesar de la asignación extremadamente poco intuitiva entre los códigos de idioma y las combinaciones. Debe haber una mejor manera...
Tuve una visita inesperada a la nueva mezquita de Cambridge. Me había fascinado su moderna arquitectura de madera desde que se inauguró y estaba dando un paseo al atardecer cuando decidí aventurarme a cruzar las puertas. Un caballero nos invitó a mi acompañante y a mí a entrar para unirnos a la ruptura del ayuno.
Fue una experiencia muy agradable conocer a la gente amable del lugar y hacer un breve recorrido por él. Ojalá la gente fuera civilizada entre sí como lo fue conmigo durante mi visita...
No hace falta decir que la arquitectura era realmente asombrosa, en particular los árboles abstractos y el árabe pixelado en los ladrillos. ¡Hay que volver de día !

Las bibliotecas públicas de Cambridge tienen horarios de apertura muy complicados, por lo que hice este gráfico para mostrar tanto cuándo abre cada biblioteca (columna de la izquierda) como para un día y hora determinados, qué bibliotecas están abiertas (columna de la derecha). Esto último es útil especialmente cuando de repente recuerdo que tengo un libro atrasado y necesito correr a una biblioteca abierta para devolverlo lo antes posible ∗ejem∗
Al hacerlo, actualicé mi función de Python 2 para leer y almacenar en caché páginas web, imágenes, etc.:
# do_refresh_cache = True import os , urllib2 , time def read_url ( url , headers = {}, path_cache = None , is_verbose = True ): if ( path_cache es None ): file_cache = os . path . basename ( url ) path_cache = os . path . join ( ' %s .cache' % ( os . path . splitext ( __file__ )[ 0 ]), file_cache if ( len ( file_cache ) > 0 ) else ' %s . htm' % ( os . path . basename ( url . rstrip ( '/' )))) if (( 'do_refresh_cache' en globals () y do_refresh_cache ) o ( no os . path . isfile ( path_cache ))): request = urllib2 . Request ( url , headers = headers ) try : html = urllib2 . urlopen ( request ) . read () except urllib2 . HTTPError as e : html = '' ; print ( e ) try : os . makedirs ( os.path.dirname ( path_cache ) ) excepto OSError : pasar con open ( path_cache , ' wb ' ) como f_html : f_html.write ( html ) if ( is_verbose ): print ( ' %s > %s ' % ( url , path_cache )) time . sleep ( 1 ) ## evitar error de límite de velocidad excedido else : with open ( path_cache ) as f_html : html = f_html . read () if ( is_verbose ): print ( '< %s ' % ( path_cache )) try : html = html . decode ( 'utf-8' ) except UnicodeDecodeError : pass return htmlEl recurso se almacena en caché en una ruta determinada [si no se especifica, el nombre base de la URL (si está en blanco, el nombre de la última carpeta en la URL seguido de .htm ) en una carpeta llamada el nombre del script de Python con la extensión reemplazada por cache ] de modo que las ejecuciones posteriores no necesiten recuperarlo nuevamente. Si la variable global do_refresh_cache es True , siempre se recupera. Se agrega un retraso de un segundo para evitar saturar el servidor web. Luego, el recurso se devuelve como una cadena Unicode.
El siguiente ejemplo obtiene la página de horarios de apertura de la biblioteca del Consejo del Condado de Cambridgeshire usando un encabezado falso simple. Descubrí que el servidor web rechaza las solicitudes sin un agente de usuario sensato . html_all se puede analizar según sea necesario con xml.etree.ElementTree o expresiones regulares .
url = 'http://cambridgeshire.gov.uk/residents/libraries-leisure-%26-culture/libraries/library-opening-hours/' headers = { 'User-Agent' : 'Mozilla' } html_all = read_url ( url , headers = headers )Espero hablar sobre esta y otras técnicas para generar SVG automáticamente usando Python en Wikimania 2019. ¡Cruzo los dedos !
Parece que hay cierta fascinación con mi antiguo archivo gráfico: Voyager_2_velocity_vs_distance_from_sun.svg ; aparece regularmente en lugares aleatorios de la Web. Pensé que sería genial tener también un mapa de las cinco sondas interestelares actuales , pero es sorprendentemente difícil de encontrar. Incluso la NASA solo tenía uno hasta principios de los años 90, antes del lanzamiento de New Horizons . Así que, con cierta dificultad, logré encontrar dos sitios que proporcionaban las coordenadas heliocéntricas de estas naves espaciales y los planetas para cada día durante un período de varias décadas: COHOWeb y Horizons On-Line Ephemeris System.
En un tránsito largo, escribí un script en Python para cotejar los datos en una tabla, para el primer día de cada mes. Luego actualicé mi script habitual, casi políglota, para trazar vistas ortográficas, con suerte mostrando claramente cada trayectoria, especialmente las ayudas gravitacionales .
¡Me pregunto si es el primer mapa que muestra las cinco sondas hasta la fecha !
ACTUALIZACIÓN DEL 22 DE ENERO DE 2019: Agregué Ultima Thule al gráfico. Supongo que eso es una ventaja de renderizar el SVG en Python: es fácil agregar nuevos cuerpos que New Horizons encuentre en el futuro.
Hacía tiempo que sabía que la relación entre los volúmenes de un cono, una esfera y un cilindro del mismo radio y altura era 1:2:3; Arquímedes consideró su descubrimiento de la relación 2:3 su obra maestra .
Por eso me quedé asombrado al descubrir por mi cuenta que la proporción de sus áreas superficiales totales, incluidas las tapas, era ϕ :2:3 (vale, Arquímedes descubrió el bit 2:3).* Es una aparición completamente inesperada de la proporción áurea , así que tuve que actualizar mi antiguo dibujo con mi hallazgo. Una ecuación con ϕ y π : ¿qué tan genial es eso?
* La superficie curva del cono se puede aplanar en un sector de radio r √5 (usando el teorema de Pitágoras) y longitud de arco 2 π r (la circunferencia del casquete). Como un círculo completo de radio r √5 tiene una circunferencia de 2 π r √5, nuestro sector subtiende 1/√5 de una revolución, dando un área de 1/√5 · π ( r √5)² = π r ²√5. Agrega la tapa y el área total es π r ²√5 + π r ² = √5 + 1/2 · 2 π r ² = ϕ · 2 π r ² .
PS Otra coincidencia es que las proporciones de los volúmenes y las áreas de superficie de la esfera y los cilindros son de 2:3. Como en el gráfico de la derecha, la proporción entre el área de superficie y el volumen de un objeto disminuye al aumentar la redondez y el volumen. Es curioso que, al pasar de la esfera al cilindro, la redondez disminuye mientras que el volumen aumenta exactamente al mismo ritmo, de modo que la proporción se mantiene .
Charles Matthews me convenció para que hablara sobre las imágenes en Wikidata en el taller de ayer. Después de una noche de estudio, me encontré con esta presentación improvisada que trata sobre
Magnus Manske amablemente participó, respondió preguntas y señaló errores en mi comprensión.
También mostré algunos de mis SVG SMIL: la animación del Reloj Corpus fue especialmente popular.
En definitiva, ¡un magnífico día de intercambio de conocimientos !

Los filtros SVG permiten efectos divertidos, como en la luz animada en la animación de nieve que aparece a continuación, pero también les encontré algunos usos prácticos. Los más simples pueden ser las sombras paralelas para hacer que las escenas pseudo-3D sean más realistas, como las sombras paralelas suaves en el gráfico del número de Platón. Para mantener el filtro lo más simple posible, se pueden hacer dos copias de los objetos; al aplicar el filtro a la copia inferior, las áreas opacas se vuelven negras y se difuminan:
<filtro id= "filter_blur" > <feGaussianBlur en= "OrigenAlfa" stdDeviation= "2" > </filtro> Por el contrario, se pueden difuminar y convertir en blancas las áreas opacas para crear un brillo alrededor de los objetos, como el texto, para que sea más fácil de leer. La etiqueta feColorMatrix colorea las áreas difuminadas de blanco y las hace menos transparentes, de modo que el contorno sea más nítido. La combinación con SourceGraphic evita la necesidad de tener dos copias del objeto:
<filter id= "filter_glow" > <feGaussianBlur en= "SourceAlpha" stdDeviation= "1" resultado= "desenfoque" /> <feColorMatrix en= "desenfoque" tipo= "matriz" valores= "0,0,0,0,1 0,0,0,0,1 0,0,0,0,1 0,0,0,8,0" resultado= "blanco" /> <feBlend en= "SourceGraphic" en2= "blanco" /> </filter> El último ejemplo es algo que quería hacer desde que publiqué esta pregunta sobre la aplicación de un contorno graduado a una forma, en particular el segundo caso. Un filtro lo resuelve de manera elegante; después de difuminar, el contorno se erosiona para poner en negrita el límite y luego se compone utilizando el operador out :
<filter id= "filter_outline" > <feGaussianBlur stdDeviation= "4" result= "blur" /> <feMorfología in= "blur" operator= "erose" radius= "4" result= "erose" /> < feOperador compuesto= "out" in= "SourceGraphic" in2= "erose" /> </filter> Esta imagen de una cancha de tenis libre muestra mi primer uso de las dos últimas técnicas, en las etiquetas de texto y los límites de los pabellones. ¡Diviértete con los filtros !

Esta pregunta me hizo reflexionar sobre la probabilidad de que aparezcan blasfemias en las cadenas Base64 que utilizo para incrustar mapas de bits en mis SVG. Como estimación de orden de magnitud, supongamos que la cadena consta solo de letras y no importa si se usan mayúsculas o minúsculas, una cadena aleatoria de cuatro letras tiene 1/26 4 ≈ 1/456 976 probabilidad de que coincida con una palabra de cuatro letras dada. Una cadena de 1 MB tiene alrededor de 1 millón de estas cadenas, por lo que espero alrededor de dos coincidencias. Hice una búsqueda sin distinción entre mayúsculas y minúsculas de la palabra F en mi archivo de 1,9 MB:Leonardo_da_Vinci_monument_in_Milan.svg (que tenía cadenas separadas, pero eso es lo suficientemente cercano) y de hecho obtuve tres instancias. ¡Espero que nadie se ofenda por mi SVG !
Me recordó a la locura de desacreditar el código bíblico en Cambridge alrededor de 2010. Al buscar el artículo, encontré que el PNG de la derecha era difícil de leer porque el texto estaba en mayúsculas y los "códigos" iban de abajo a la derecha a arriba a la izquierda. Pensé que podía hacerlo más legible y vectorizarlo al mismo tiempo: puse las palabras alternativas en negrita. Casualmente, en el caso correcto, solo la B inicial estaba en mayúscula. Pero el mejor cambio fue usar 21 columnas en lugar de 33; con el desplazamiento correcto, esto hizo que el "código" fuera de izquierda a derecha y no cruzado.
Como había escrito Python que realmente buscaba en el texto, decidí hacer una versión con marca local con "wiki" y "pedia" (no pude encontrar "wikipedia"). Genesis tenía muchas coincidencias, así que elegí una en la que estaban muy juntas. No pude evitar el cruce sin distorsionar demasiado los "códigos" o hacerlos de derecha a izquierda. Ver más abajo...
Acabo de enterarme del calendario juliano revisado, que mejora el calendario gregoriano . Su fórmula para decidir si un año centenario (número de año terminado en "00") es bisiesto no era obvia, así que decidí dibujar esta tabla, que deja claro que hay 2 años bisiestos cada 9 años centenarios, en comparación con 2 cada 8 en el gregoriano. Su diseñador dispuso inteligentemente los dos en el lapso actual de 900 años para que coincidieran con 2000 y 2400, lo que significa que los calendarios coincidirán perfectamente para los años 1601 a 2799, a pesar de la reforma del calendario gregoriano . ¡Eso debería ser suficiente por un tiempo !
El Wikitext en sí no es demasiado interesante, simplemente envuelve la tabla en un div que flota hacia la derecha para simular un cuadro de información. No pude usar la clase infobox porque las celdas de la tabla dejaron de estar alineadas al centro. También aprendí el uso de template:navbar para permitir que los editores editen plantillas más fácilmente y me divirtió la gran cantidad de plantillas de marcas de verificación y de cruces .
Me alegra mucho que Vincent Mia Edie Verheyen me haya contactado recientemente para pedirme ayuda con SVG interactivos y animados. ¡Finalmente encontré a alguien que comparte mi interés en los SVG dinámicos !
Descubrió que muchas técnicas CSS o SMIL aún no funcionan con Internet Explorer/Edge. La única interactividad fiable parece ser el desplazamiento del cursor, las sugerencias de herramientas, los hipervínculos y el cambio del puntero (cursor). Aparentemente, el selector :active también permite hacer clic, pero el usuario debe presionar el botón continuamente. Parece que la industria se ha pasado a JavaScript (no es una sorpresa en realidad) – ¿hay alguna esperanza de que Wikimedia permita al menos algo de Javascript en las cargas de archivos? :-(
De todos modos, me alegró aprender de Vincent sobre la etiqueta de símbolo , tal como se usa en este SVG animado. Puede hacer más que los objetos nombrados en defs que he estado usando, como escalar el objeto para que se ajuste a un ancho y alto determinados (conservando opcionalmente la relación de aspecto). También admite el atributo viewBox como la etiqueta svg . http://sarasoueidan.com/blog/structuring-grouping-referencing-in-svg/ tiene un tutorial.
Una limitación es que las partes del símbolo con coordenadas negativas se recortan. Una solución es agregar overflow="visible" , por ejemplo
<símbolo id= "cosas" desbordamiento= "visible" > <rect x= "-10" y= "-20" ancho= "30" alto= "40" /> </símbolo> <use xlink:href= "#cosas" x= "50" y= "60" /> Además, se puede mover el símbolo especificando los atributos x e y en la etiqueta de uso , donde antes podría haber usado transform=translate(50,60) . ¡Tres hurras por el intercambio de conocimiento bidireccional en Wikimedia !

He estado experimentando con STL durante el último mes. User:Romanski me recordó que la mayor parte de lo que he hecho, incluidos los fractales, ya se puede hacer con otras herramientas. Sin embargo, un área a la que creo que puedo contribuir son los modelos de elevación planetaria, como este. Para mí, un modelo 3D, particularmente uno físico, hace que la forma sea mucho más clara que un mapa topográfico, especialmente las características de las regiones polares. (Quizás una cosa que se pierde es que el hemisferio norte está significativamente más bajo que el sur). Es una pena que la mayoría de los visores STL, incluido el de Mediawiki, no admitan colores; eso definitivamente abriría un mundo completamente nuevo de posibilidades.
De todos modos, mirando el historial del archivo , se puede ver cómo evolucionó mi técnica:
Hice otros dos modelos con el método final:
El siguiente paso puede ser utilizar una red irregular triangulada , pero eso tendrá que esperar a otro día...
Como en la entrada del mes pasado que aparece a continuación, Wikipedia permite colecciones de imágenes que se ajustan al ancho del navegador mediante la etiqueta <gallery> . Sin embargo, mi lado asperger se enoja cuando solo hay una imagen solitaria en la última fila ☹
Me di cuenta de que, aunque no puedo controlar cuántas columnas habrá, sí puedo controlar cuántas imágenes hay en la galería, así que hice un pequeño script en Python para generar una tabla que resalte los números "buenos". Obviamente, es inevitable que quede uno cuando p = kc + 1 para cualquier entero k, pero ¿qué pasa con los demás números?
Además de los números altamente compuestos como 6, 12 y 60, existen números sorprendentemente "buenos" como 14, 38 y 44. Por otro lado, 10 y 36 son "malos" ya que dejan 1 resto con 3 y 5, respectivamente. Y los números posteriores a los altamente compuestos, como 13 y 25, son especialmente "malos"...
Como nota al pie, aprendí que en tipografía, una sola palabra en una línea al final de un párrafo se llama huérfana . ¡Parece que no soy el único al que le molesta !
Me encantó saber de Charles Matthews que Wikimedia Commons ahora permite cargar archivos 3D en formato STL , siempre y cuando admitiera color, transparencia, animación, etc.
Como en una vida pasada disfruté del modelado 3D, me dispuse a crear los modelos que se muestran a continuación utilizando scripts de Python. Como los archivos STL no permiten incrustar los scripts como comentarios, los agregué a las páginas de descripción de archivo. Lamentablemente, encontré artefactos en el visor de Wikimedia y, ocasionalmente, en la miniatura . He comprobado que la dirección de los vértices de las facetas es en sentido antihorario, las normales son sensatas y los polígonos no están duplicados. Parece que sucede más donde el poliedro es delgado. Todos estos poliedros se representan correctamente en http://viewstl.com. Veamos si se pueden arreglar...

I had the good fortune to visit the Griffith Observatory and had a personalised explanation of its Foucault pendulum. Seeing the marks from 0 to 41 around the rim, I asked how long it takes to rotate 360° for a given place and was told it's the sine of the latitude.
Checking Wikipedia, the angle a Foucault pendulum precesses is indeed linearly proportional to sin(latitude), but there was no illustration showing the precession period. I thus drew this graph showing both the precession per day and its period. Curiously, at the axes' scales, 24 hours coincides with −360° and 4 days with 360°, letting me share the gridlines.
Footnote: I found out that the "day" is a sidereal day; the earth itself orbits the sun, so the direction of noon changes from day to day. Instead of 24 hours, it's ~23.93447 hours, but that's indistinguishable on the graph. Griffith Observatory's 34.11856°N yields a precession period of 42.67 hours, a bit more than the markings!
When uploading a derived image, I previously found specifying the file(s) from which it wad derived a bit clumsy; I could use, for instance,
none of which simultaneously lets
I thus decided to create a template on Commons:
<table style="display:inline;border-collapse:collapse;"><tr><td>[[File:{{{1}}}|thumb|none|[[:File:{{{1}}}|{{String replace|{{{1}}}|_| }}]]]]</td></tr></table>This automatically generates a thumbnail with the filename as a caption linking to the file description page (I'd have preferred it to link directly to the actual file, but couldn't find a way to derive its URL from just the filename):
The uploader can now simply transclude the template with the filename (without "File:") as the first parameter:
{{source thumb|FILENAME}}To make the caption more readable, I replaced underscores with non-breaking spaces. I also enclosed the thumbnail with an inline table, so that multiple thumbnails can flow side by side instead of being stacked one above another.
If there's demand, I'll add more parameters to fine-tune the thumbnail.
UPDATE 14 MARCH 2018: {{filepath:FILENAME}} gives the file URL, hence
<table style="display:inline;border-collapse:collapse;"><tr><td>[[File:{{{1}}}|thumb|none|link={{filepath:{{{1}}} }}|[[:File:{{{1}}}#filelinks|{{String replace|{{{1}}}|_| }}]]]]</td></tr></table>UPDATE 21 OCTOBER 2018: I added the option of specifying the language for internationalised SVG using a second parameter, as in these thumbnails:
{{source thumb|FILENAME|LANG}}I've finally found out how to have "inline" tooltips in an SVG which appear when hovered, yet allow fill and stroke opacity to be fully controlled on hover: set the unhovered font-size to a tiny value, say, 0.1 px, and the hovered one to the normal size. In this world map of confirmed impact craters, this allows both stroke and fill of a circle to fade when the user hovers over the map, but not the circle. The advantage of "inline" text is that it appears immediately on hover, unlike a regular tooltip, and allows limited styling, such as 2-columns or left and right-aligned text.
I also found that using the link paramter of the thumbnail directly loads the SVG on clicking the thumbnail, instead of the file description page. The file description page can still be accessed by clicking the icon at the right of the caption.


It's great that Cambridge has an annual event where private establishments open their doors, normally a weekend before London Open House.
This year's Open Cambridge saw the public opening of Eddington, the centre of the North West Cambridge Development.
Being the resident village busybody, I couldn't help visiting, joining some tours and capturing the sights. My favourite was Fata Morgana, a "tea house" made almost entirely from steel mesh. The semi-transparent surfaces made the experience surreal. I got to chat with its artists, too, and learn about its creation.
Not realising that someone had just created an article on Eddington itself, I created North West Cambridge Development and nominated it for Did You Know. (Well, at least I didn't know how many hoops one had to jump through to get an article into Did You Know.)
And when I have more time and inclination, I'll try merging both articles...


I noticed that a full HD screen has just over 2 million pixels (1920 × 1080 = 2 073 600) and had the idea of a two-dimensional visualisation of the size of one million to complement my three-dimensional one to the left.
By using a checkerboard pattern, I could show one dot for every two dots. The naive approach would result in a big blob of a million dots without any grouping, so I wondered if there might be a way to separate them into 1000 tiles of a thousand each. Having 10 rows of 100 columns would "use up" 9 rows and 99 columns of pixels to separate the tiles, resulting in 1821 × 1071 = 1 950 291 pixels, just shy of the 2 million pixels needed. However, 10 rows of 10 columns gives 1911 × 1071 = 2 046 681 pixels, so I'm on the right track...
I could use the background of the dots to separate tiles of 1000 dots. I settled on white and very light grey to make the difference just visible yet not too distracting. Interestingly, 19 × 106 = 2014, i.e. 1007 dots, so each group of 10000 dots can be 190 pixels wide and 106 pixels tall. A 10×10 matrix of these would leave a neat 20 rows and 20 columns of pixels to separate the groups. To make the groups easier to count, I divided them as follows: 2_1_2_1_2_4_2_1_2_1_2, where _ represents a group, in both dimensions. As 7 dots had to be removed from each tile, I removed 3 from one corner and 4 from another, conveniently resulting in ticks appearing in each group.
Hacking up the Python script (which uses the png.py module) on file:one_million_dots_1080p.png, a bit of tweaking to make the graphic symmetrical, and ta-da – 1 million black dots in full HD!

magine a 138-page book chronicling the history of time. Each page has exactly 100 lines, and each line, exactly 100 letters. The first letters on the first page describe the most recent events; the last letters on the last page, the beginning of the Universe as we know it. If the amount of text is linearly proportional to time, how much of this tome narrates written human history?
Well, with 13.8 billion years denoted by 138 pages of 10000 letters, each letter represents 10000 years. Thus, written history is worth about half a letter!
This graphic shows where some other notable events lie. Note that everything involving humans lies on the first line, representing the most recent 1 million years.
Going down two-thirds of a page, we come to the big die-off of the dinosaurs 66 million years ago. At the end of the first page, 100 million years ago, we're firmly in dinosaur and reptilian territory. Just five pages later (500 million years earlier), complex animals hadn't evolved. After the tenth page (1 billion) years, the most complex lifeforms were green algae.
A third of the book in, the 45th page marks the formation of the Earth, the Sun and much of the rest of the Solar System. Most is unknown about the Universe until perhaps the last 8 or so pages when the first galaxies formed.
The final page, likely the 138th, is once again a hive of activity, where much of the early Universe takes place. Exactly how many lines and letters it has, noone knows...
I hope this analogy gives another perspective on the timeline of the Universe. Though one might bemoan our insignificance in the big picture, I find it amazing that scientists were able to discover these milestones in just the first half-letter.
P.S. At the same scale, how long is the Diary of the Universe to people who think it started in 4004 BC? Six-tenths of a letter! ୯ ͡° ͜১͡° ੭


The graph on the left employs a clever technique to have gridlines in different units, such as metric and imperial, on the same graph: by having them straddle the line!
I wondered if it might work for any odd number of graphs, and drew this month's graphic. Getting the gridlines to alternate between the curves was tricky, but creating clip-paths by alternating the directions of the paths worked. Each set of gridlines could then be made up of rects textured with their corresponding patterns. I even managed to reasonably smoothly transition from feet to miles for imperial altitude. And of course, multiplicative factors between units appear simply as translations on a logarithmic scale.
It was fun picking reference altitudes, though I couldn't find a good one between ISS and GPS orbits. It's also rather surprising how good the approximation is, and how similar the straight-line and along-Earth's-surface distances are, all the way to the official boundary of outer space.

User:Ethanmayersweet suggested that I update my unexpectedly popular graphic and I thought it would be the perfect opportunity to update the map to an azimuthal equidistant projection – I'd found it mildly annoying that the radii of the rings weren't to scale, and much of the globe (especially mainland USA, whose readers would most likely be interested in) was hidden.
User:Jason Davies had usefully uploaded File:North-korean-missile-ranges.svg, but I preferred a coloured globe without coastline shading. The other thing I wasn't so keen about was the 5 MB file size. So I wrote this Python script to
The script could have combined multiple "h" and "v", and handle commands other than "M", "L" and "Z", but that will have to wait until another day. That reduced the total file size (even after "beautification" and updating the ranges) to 162 KB, a reduction of 97%!
By the way, I found it curious that UK and mainland USA (and Africa) are just beyond 8 000 km – coincidence?


After hearing about the Menger sponge at a talk about fractals in this year's Cambridge Science Festival, I challenged my companion to guess what a cross-section along a space diagonal and passing through its centroid looks like.
Back home, it occurred to me that I could use the constructive solid geometry feature of POV-Ray to automatically generate cross-sections, and decided to make an animation of the cross-sections along the space diagonal similar to http://youtube.com/watch?v=fWsmq9E4YC0 but viewed perpendicular to the section so that each section is a true view.
The biggest challenge was coming up with an efficient way to create the sponge. The method I used to render the level-4 tetrix on the left would result in 204 = 160 000 cubes – far too strenuous for my measly computer!
I eventually decided to subtract three orthogonal sets of long holes from a simple cube. My initial arrangement resulted in artifacts due to holes from different levels overlapping, but I managed to find a set without overlap – see my POV-Ray source code below if you're interested.
Additionally, I wanted to use a perspective projection for a more realistic look, but still wanted to keep every section at the same scale, so I had to translate the cube at exactly the rate which keeps the cross-section plane in place. To confirm that I got it right, I replaced the sponge with a simple cylinder with its axis perpendicular to the plane.
After a day rendering the 55 frames (27 × 2 + 1 – chosen so that every vertex has a plane passing through it), I thought the colour was a bit bland, so modified the palette after converting them into GIF in XnView's batch mode. Good thing I decided to turn off anti-aliasing to increase rendering speed.
I also decided to add pauses at the level-0 vertices, and of course, a longer one at the cross-section through the centroid.
Lastly, I came up with a tidier presentation of my POV-Ray source on the file description page, so that anyone can continue my work:
Now I'm tempted to make more animated cross-sections, and one that comes to mind is a rotating double cone to generate conic sections!

Three years on from its first publication, I've updated my periodic table of the origin of the chemical elements, made infamous by NASA choosing it as Astronomy Picture of the Day. I was surprised by its selection (it wasn't me who submitted it for consideration – I wasn't even particularly proud of it, as I'd quickly hacked it together after attending a talk showing the figure from which it was derived) and the subsequent criticism of its veracity.
Since then, astronomer Jennifer Johnson created a more well-researched version and I decided to combine with her data with some "improvements":

I became interested in the Seven Wonders of the Ancient World after watching a documentary and read the Wikipedia article. Seeing room for improvement of their timeline, I set about drawing one.
It felt a little clumsy as the massive range of the Great Pyramid of Giza compared to the others caused huge gaps to appear.
I wondered, "Why not fill them with useful information?" and thus added a map and silhouettes to scale, with dimensions obtained as far as possible from their respective Wikipedia articles.
The outlines show how amazing an achievement the building of not one, but two pyramids of comparable size was, 2000 years before the other wonders.
Lastly, from the scale of the timeline, it seems a shame that we just missed living in a time when three wonders existed. If only they hung on for 600 more years!

I learnt that SVG filters can be animated using SMIL and added an ambigram that reads Merry/Happy and Christmas/New Year to my CSS snow animation. Happy 2017!


I had just realised that the block-stacking problem article lacked an illustration despite my interest in harmonic series. This presented a good opportunity to experiment with an idea to use affine transformation matrices (which I explored last month) to transform bitmaps to make more realistic pseudo-3D graphics.
In the SVG, the upper-right 3×3 swatches in the image on the left were split into individual textures, each assigned to a pattern. Appropriate affine transformations were applied to the faces of each block, some overlaid with semi-transparent black to simulate shading, and defined as a group. The fill parameter of each group was assigned a texture pattern, and the block moved into position.
It's a shame that SVG doesn't do perspective transforms (even though CSS does), so I'm limited to parallel projection. Still, that suits technical illustrations where conceptual clarity takes precedence over geometric fidelity.
Expect to see more textured SVGs!

UPDATE 24 FEB 2020: This example simulates wood textures with SVG filters – uniting blur-filter shadows, turbulence-filter textures, affine transforms and my 4-3-2 projection ideas.

Back in 2012, I discovered an aesthetically pleasing 3D trimetric projection that lets one construct semi-realistic-looking scenes using vectors with components comprising small integers, namely
assuming the image y-axis is positive downwards. An added advantage over dimetric or isometric projections is that the rear edges and vertex of a cube does not overlap with a front one, so that they can be clearly shown. Curiously, a 2 × n × 1 block has the same width and height.
I also found some useful affine transformation matrices to automagically apply rectangular textures onto the three faces of a cuboid:
As can be seen from the "F" pattern, I had to mirror the left face horizontally and the top face vertically so that they could all start at the nearest vertex. This has negligible effect on symmetrical patterns such as gridlines, but asymmetrical ones have to be either pre-flipped or the matrices must be changed.
With this useful shape, I drew a variety of illustrations including these:
27 SEP 2019 UPDATE: commons:category:4-3-2 trimetric projection created.


A few days ago, I found that Wikipedia lacked an illustration showing the key values of the general univariate quadratic function y = ax² + bx + c and so drew the graphic on the left. Just as I thought my work was done, I found out about a method to graphically find the complex roots of such a function without real roots – eons since I left high school!
Back to the drawing board, I modified my earlier graphic to visualise the method and created the template on the right for easy inclusion in Wikipedia articles.
The trickiest bit was creating the text objects containing mathematical expressions. I employed a neat device in which a fraction is constructed from
For example, −b/2a is created with the following SVG code (note the wrapping of the line before the ">" character to avoid introducing meaningful whitespace):
<text transform="translate( 130, 40)" x="0" y="0" ><tspan>−</tspan><tspan font-style="italic">b</tspan><tspan x="0">__</tspan ><tspan x="-10" dy="1em">2</tspan><tspan x="10" font-style="italic">a</tspan></text>I would have preferred the minus sign outside the fraction: −b/2a , but that would have required the extra hack below...
For the coordinates (−b/2a, −(b²−4ac)/4a) , I had to manually create a separate "( , )" text object in larger font (with some stretching in the y direction to avoid the brackets looking too thick) to wrap around the two functions. Is there a better way? Let me know!
I thought I'd do a little part of documenting Wikimania 2016 and the village of Esino Lario by shooting 360° spherical panoramas of notable places using the Photo Sphere feature of the native Android camera app of my Nexus 7:
http://wikimania2016.wikimedia.org/wiki/User:Cmglee/panoramas
The page also features Dschwen's Pano360 panoramic viewer and "Tiny Planets" generated by the same app.
For optimum results, one should really use a tripod or a specialised camera, as doing it by hand results in many stitching errors – nevertheless, the poor man's method doesn't require much beyond an Android phone or tablet with gyroscopes, and lots of patience!
As I discussed with user:Pigsonthewing on my Commons talk page, in case anyone wants to shoot some, here are some techniques for better results:
Shame I discovered them only as I went along, but I suppose one gets better with practice...
I noticed editors adding translations into File:Phase_diagram_of_water.svg and learnt that, using the switch tag and systemLanguage parameter, an SVG file can contain multiple languages. While visiting Milan's Pinacoteca di Brera after Wikimania, I realised that I could hack this mechanism to highlight different parts of an illustration in different articles. Back home, I successfully tested it on File:comparison_of_pyramids.svg as on the left. I'll use another example as I'd written on the pyramids SVG below.
In its SVG, each highlighted version is amended as follows:<switch><use xlink:href="#id" systemLanguage="CODE"/></switch>where CODE is one of these codes. As codes must be valid, I picked ones which look similar, yet are relatively rare to not conflict with real use: from left to right, ts, ca, cu, os, or, ml and kl.
To use the SVG, add lang=CODE in the image's Wikitext and it appears as on the right:[[File:Tallest_towers_in_the_world.svg|thumb|lang=cu|Comparison of the CN Tower with the world's seven tallest towers]].
I create the template:Tallest towers in the world.svg to make it easier to use. The first parameter is the code (set to blank for no highlighting) and the second is a custom caption snippet (set to blank to use the name of the page it appears on, a trick described below):{{tallest towers in the world.svg|CODE|CAPTION SNIPPET}}.
I had the privilege to share accommodation with user:Shangkuanlc at Wikimania. While chatting about my adventures in dynamic SVG, he was fascinated with this silly little game I made to showcase what could be done with SMIL, and very kindly translated it to Chinese. We talked about other ideas for SVG games – including an Angry Birds parody I named "Anti-Birds", a skeet shooting game where the player tries to snipe, in mid-air, birds about to crash into the usual porcine architecture!
I realised, however, was that games often have random elements but SMIL and SVGs without JavaScript are normally deterministic. After discussion with user:Niedzielski, I thought of a way to simulate random events by rapidly rotating an invisible pinwheel of triggers in front of a button. Due to its rapid rotation and invisibility, the trigger that is clicked is practically random. I created this "wheel of fortune" prototype to demonstrate the concept ("Show triggers" toggles the visibility of the triggers).
The translation effort also revived the idea to rewrite an updated SVG translation tool. I had previously used Jarry1250's SVG Translate but it no longer works, and also requires the user to manually fill in all the fields. I learnt that Pywikibot is a good platform to use, and attended a training session and spoke with user:Yuvipanda. Let's see what I can come up with one of these weekends...
... so I'm giving a talk and training at Wikimania 2016. Come join us on Saturday 25 June 2016 if you're in town. For a preview, below is my slide deck...

An advantage I thought Perl had over Python was the ability to interpolate or embed variables directly into a string, such as
print "Hello $name";where Python uses format or % :
print "Hello %s" % (name)print "Hello {0}".format(name)which gets clumsy for long strings or a large number of variables.
That was until I learnt that I could do this (as long as name is a local variable):
print "Hello %(name)s" % locals()print "Hello {name}".format(**locals())print "Hello {name:s}".format(**locals())print "Hello {name!s}".format(**locals())I wondered if it would be even better if name could be an arbitrary expression and not just a variable e.g. name.upper() to capitalise the whole string or len(name) for its number of characters (zero-padded to eight hexadecimal characters). And so I wrote the following:
import redef fmt(string): ## string.format(**vars()) using tags {expression!format} by CMG Lee def f(tag): i_sep = tag.rfind('!'); return (re.sub('\.0+$', '', str(eval(tag[1:-1]))) if (i_sep < 0) else ('{:%s}' % tag[i_sep + 1:-1]).format(eval(tag[1:i_sep]))) return (re.sub(r'(?<!{){[^{}]+}', lambda m:f(m.group()), string) .replace('{{', '{').replace('}}', '}'))which lets me do this:
print fmt("Hello {name.upper()}")print fmt("characters:{len(name)!08x}")If there is no format string, 's' is assumed, but if the expression contains !, such as {'differ' if 1 != 2 else 'equal'!s}, the format string must be specified. To escape braces, repeat it: fmt("{{this is not a tag}} {'but this is'}")
It's far from perfect: if the expression contains }, such as {{'a':1,'b':2}['a']!d}, it can't tell which } the closing brace of the interpolation is, as regular expressions cannot count nested brackets, and error messages are quite ugly.
The example graphic illustrates the German tank problem dating back to WW2. As paraphrased for a sporting mate:
Earlier this year, Cambridge hosted an e-Luminate festival. Among artistic displays of light were talks highlighting the inaccessibility or unaffordability of home lighting in some developing countries.
I thought it would be useful to show the disparity of light usage on a world map, and decided to encode different dimensions of data in different channels of a colour image, as I had done in this heightmap. I found assorted bitmaps in equirectangular projection at NASA, and rescaled and copied them into different channels in The GIMP:
Elevation was derived from topography and bathymetry maps. After some experimentation, I found that each could be independently normalised, with low elevation being dark and vice versa, and added together. This resulted in a sharp boundary between land and sea, and also darkness in lowlands where there is more population and lights. Coastlines and country borders were rendered from a modified blank Commons map after setting the fill and stroke of each SVG path to contrasting colours.
To avoid the Chukchi Peninsula in east Russia from being chopped in half, the map was shifted by 10° west so that it wraps around at the 170th meridian west — I later found that the peninsula is still broken up and could have chosen 168.98°W, passing between the Diomede Islands.
The finished piece shows the stark contrast between developed and developing countries: USA and Europe mostly swathed in green, and India, China, Indonesia and Nigeria in red – as others have pointed out, there is a large shift just across the border between the two Koreas. Large cities, especially in Europe and Japan, glow yellow from both high population density and light output.
As expected, most habitation is in the lowlands, but there are lights in the Rockies and Andes (cyan) and dense population around the lofty shores of Lake Victoria and Ethiopia (purple).
And that's my new wallpaper!
I had tried using a CSS background image of a diagonal line, but this doesn't scale well with arbitrary text.
Then one day, I suddenly thought of using a background gradient, as I had done for the table in Electromagnetic spectrum. The gradient runs from the bottom-left to the top-right of the cell, and is the default header-cell grey everywhere except from 49% to 51% of the way where it transitions to a darker grey:
background:linear-gradient(to top right,#f2f2f2 49%,#aaa,#f2f2f2 51%)The darker colour and transition width were chosen so that, for typical cell sizes, it looks like a diagonal line running across the cell, similar in appearance to regular cell borders. The cell is really still one entity, so the spacing of the text labels has to be adjusted to straddle the line. Though it works on Chrome, Internet Explorer and Firefox, two limitations are that the labels easily overrun the "line" if the user is not careful, and that the background of the header cell cannot be easily changed. An alternative I tried is to have a div completely fill the cell and overlay a transparent-dark grey-transparent gradient, but my tests resulted in small gaps between the diagonal line and the cell borders, ruining the effect.
To use the template, create a header cell using ! followed by {{diagonal split header|HEADER-OF-ROW-HEADERS|HEADER-OF-COLUMN-HEADERS}}. Pad the header text with to straddle the line. Adding rowspan or colspan attributes allows it to span multiple rows or columns, as in this example for Chinese New Year:
So I've submitted an application for a scholarship and talk at Wikimania 2016 to present my ideas for interactive and animated SVG, and meet potential collaborators who might be interested to further develop them. I wrote up the article
See what you think!


A year ago, my computer died on me and I thought I had lost a useful little tool which shows coordinates of any point in an SVG file under development to allow the user to quickly trace a shape from a bitmap, even when zoomed in. I discovered that I had saved a copy as a comment in File:Descriptive_geometry_lines.svg and took the opportunity to update it with new things I've learnt about JavaScript:
<script type="text/ecmascript"> /// SVG coordinate picker by CMG Lee (Dec 2015) /// based on http://stackoverflow.com/questions/2930625 and 610406 function _r(p, c) { return p.replace(/~/, c); } function pickCoords(evt, doSave) { var pos = document.getElementsByTagName('svg')[0].createSVGPoint(); pos.x = evt.pageX; pos.y = evt.pageY; var ctm = evt.target.getScreenCTM().inverse(), ROUND_TO = 10; if (ctm) { pos = pos.matrixTransform(ctm); } var x = Math.floor(pos.x / ROUND_TO + 0.5) * ROUND_TO, y = Math.floor(pos.y / ROUND_TO + 0.5) * ROUND_TO, log = [x,y, x,y].reduce(_r, '#~,~ x="~" y="~"'); if (doSave) { location.href += log; } else { history.replaceState(null, '', location.href.substring(0, location.href.lastIndexOf("#")) + log); } document.getElementById('cursor' ).setAttribute('transform', [pos.x,pos.y, ROUND_TO].reduce(_r,'translate(~,~) scale(~)')); document.getElementById('crosshair').setAttribute('transform', [ x, y, ROUND_TO].reduce(_r,'translate(~,~) scale(~)')); pos = null; } </script> <path id="crosshair" d="M9999,0H-9999V9999H0V-9999H9999 M0.5,0.5H-0.5V-0.5H0.5 M1,1H-1V-1H1" fill-rule="evenodd" fill-opacity="0.5" fill="#99cc00"/> <circle id="cursor" cx="0" cy="0" r="0.1" fill-opacity="0.5" fill="#669900"/> <circle cx="0" cy="0" r="99999" fill-opacity="0" style="cursor:none" onmousemove="pickCoords(evt)" onmouseup="pickCoords(evt, true)"/>Now it not only shows the cursor's coordinates in the address bar in Firefox (sadly I couldn't update the window title by setting window.document.title ) but saves points clicked (actually when the mouse button is released). By changing the ROUND_TO value, one can change the granularity of the values, which is reflected by an overlay — leaving the inner 4 squares moves to a different value, of which centre point is the corner of the larger square of the quadrant that will be moved into.
Eager to try it out, I found a relatively simple logo on commons:Top_200_images_that_should_use_vector_graphics and managed to fix the non-uniformity in the rings in no time. As another test, I vectorised a graph from commons:Top_200_graph_images_that_should_use_vector_graphics to avoid the user having to look up the legend.
Not a bad diversion on Christmas week ୯ ͡° ͜১͡° ੭

On a visit to an astronomy observatory, I learnt about the use of a Bahtinov mask to focus a telescope. Invented only 7 years ago by an amateur astronomer, it ingeniously exploits what is normally considered an undesirable artifact: diffraction spikes. As I couldn't find a diagram on the Internet which explains its operation, I decided to draw one while awaiting the airport bus back to Cambridge.
The next time I had some time to kill waiting for another flight to board, I drew the graphic below, which describes the effect of the struts holding up a reflector's secondary mirror on the spikes.
Perhaps I've found a new way to make better use of down time at the airport!



I was delighted to see a model of a Menger sponge made of interlocking folded business card at this year's Cambridge Science Festival, so had to take this interesting perspective through its middle. Learning more about the fractal, I added several tidbits to its article, including an image of its curious cross-section through its middle.
Since the festival had been lacking its own article for many years, I also decided to write it up and include some of my more representatitve shots: Cambridge Science Festival
Inspired by a slide in one of the talks, I drew up this graphic of stellar evolution based on an unannotated rendering from NASA.
Wikipedia, Wikibooks and Wikiversity are excellent in describing things textually and graphically. However, some concepts are better explained interactively, for example, comparing members of a set or investigating the components of a system, but we are currently limited to video clips and GIF animations.
Now that Scalable Vector Graphics (SVG) is becoming well-supported in web browsers, I believe that we should explore ways to enhance articles with dynamic SVG. JavaScript or ECMAScript allows almost limitless ability for interaction and animation.
A major obstacle is that uploads with JavaScript are barred, understandably for security reasons — on a popular site like Wikipedia, cross-site scripting issues are a concern. Fortunately, SVG provides two other techniques for interactivity and animation: SMIL and CSS.
My project explores them, and aims to create demonstrations and tutorials to allow users to create dynamic content. Here are some demonstrators developed so far:
At the 24th Cambridge meetup, Charles showed us the use of templates to create navigation boxes, so I decided to create one which I would have found really useful when I studied mechanics:
The left table has translational properties, common symbols and units, while the right table has rotational ones. They are classified according to the SI base units from which they are derived, according to the scheme on the right. My only gripes about the template are what to title it (it's really more a linear-angular analogy) and the wasted whitespace especially on wide browser windows.
Pete (the wub) also showed me File:London_Underground_Overground_DLR_Crossrail_map.svg which highlights London Underground lines on mouse-click, and I've been experimenting with SVG interactivity lately, but that will have to wait for my next update...
I attended an educational Cambridge Festival of Ideas talk yesterday and was intrigued by the complexity of the territorial disputes in East and Southeast Asia.
Back home, I found that though Wikipedia's Territorial disputes in the South China Sea article describes the ongoing ones, it was difficult to see which countries were involved in which disputes. I thus decided to add a table to summarise them.
I recycled an idea I'd used on this page on the Greek Islands in Wikivoyage (the table on the right): some column headers are rotated 90° so that the table isn't too wide. I've tested it on Chrome, Firefox, Opera and Internet Explorer. Credit goes to Timwi who was instrumental in helping me developed it.
It's a shame that this technique requires manual tweaking, such as adjusting the width and height of table cells' CSS to avoid the sideways text overflowing its cell. Pity, too, that the 'BLACK FLAG' U+2691 (⚑) and 'CROSSED SWORDS' U+2694 (⚔) Unicode characters don't display correctly on my browsers — either would have made a much more appropriate icon than the tick!

Once in a while, I hear or read a comment on the exceptional hearing range (in terms of frequency) of bats, dogs and other animals. Inspired by this interesting BBC article, I decided to compare the ranges of animals for which I could find sources, including humans. For comparison, I added C (musical note) of octaves in the range, calculated from A440 (pitch standard). It seems that while bats can hear very high frequencies, their overall range (in terms of octaves) is poorer than ours. Humans aren't actually too bad, but the overall leaders are porpoises and cats, as well as, surprisingly, ferrets and cows — who would've expected that?!
This was also my first attempt at (almost) polyglot code combining SVG and Python (programming language). I had previously appended the generator Perl and Python scripts in my SVG contributions as a comment. I think that including generator code in the SVG avoids its loss and keeps it up-to-date (storing it on, say, its Commons file description page is liable to cause it to become unsynchronised, as I found with file descriptions).
However, where the static SVG contained embedded images such as File:Volcanic eruption map.svg, this increased the file size horribly. To minimise file size, I divided the SVG into two parts:
Unfortunately, I couldn't make the SVG completely valid Python code as it must start with <?xml which is invalid in Python. My poor-man's solution was to instruct the user to delete the first line. The following is an outline of the SVG file.
The first line ends with an SVG comment to comment out the start of the Python comment plus the note to the user on the second line. When the first line is deleted, the Python script immediately starts with a block comment to comment out all the SVG code:
<?xml version="1.0" encoding="utf-8"?><!--""" To recover the Python script to generate this SVG, delete the line above --><svg version="1.1" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" width="100%" height="100%" viewBox="[x] [y] [width] [height]"> <title>...</title> <desc>...</desc> <defs> ...<!-- BEGIN_DYNAMIC_SVG -->...<!-- END_DYNAMIC_SVG --> </defs> <use xlink:href="#main"/></svg><!-- Please retain this and other comments, which contain Python code to generate this SVG. """The BEGIN_DYNAMIC_SVG and END_DYNAMIC_SVG sentinel values tell the Python script where to insert the SVG generated dynamically. The top-level group with id="main" is "used", and the SVG is wrapped up with the Python code proper as an SVG comment.
Anything which the Python script wishes to dynamically output is stored in a string list called outs, which is later "joined" into a string. The final line closes the SVG comment to make it a valid SVG file. Note that the Python script must not have two consecutive dashes, as it appears like the comment is closing; the variable double_dash is a workaround.
# Store output as a group with id="main" in string array "outs"import re...# Code to compile everything into a .svg file follows...double_dash = '-' + '-' # because SVG comments cannot have 2 consecutive '-'smyself = open(__file__, 'r').read() # the contents of this very filefile_out = open(re.sub(r'\..*?$', '', __file__) + '.svg', 'w') # *.* -> *.svgtry: # use try/finally so that file is closed even if write fails file_out.write('''<?xml version="1.0" encoding="utf-8"?><!%s%s''' % (double_dash, re.sub(r'(BEGIN[_]DYNAMIC_SVG.*\n?)[\s\S]*(\n.*END[_]DYNAMIC_SVG)', r'\1%s\2' % (''.join(outs).strip('\n')), myself))) # replace dynamic SVG block with contents of "outs"finally: file_out.close()# SVG-Python near-polyglot framework by CMG Lee (Oct 2014) -->All this seems unnecessarily convoluted; if you can think of a better way, do let me know!

I had the honour of meeting 1973 Nobel physics prize winner Emeritus Professor Brian Josephson on Saturday at a walking tour in northeast Cambridge led by Charles Matthews, one of the pioneers of Wikipedia. In conjunction with Wiki Loves Monuments, Charles decided to hold a tour of lesser-known listed buildings in Cambridge, viz. the Cambridge Museum of Technology and Chesterton Tower, before the regular Cambridge meetup.
We also saw the Riverside Bridge, swift tower, Logan Meadow nature reserve and Elizabeth Way Bridge, before returning to CB2 cafe for hot chocolate. Perhaps due to the rain, only 3 people turned up. I suggest that we have more walks, but after meetups, so that attendees may be persuaded to join in!


User:Wdcf had contributed an insightful graphic giving an overview of the complicated history of Malaysia. Over three years ago, I coloured the background stripes and added a map to show the locations of these political entities.
After learning SVG, I thought that it could be redrawn as in vector graphics and finally set about the task this weekend. I took the opportunity to add recent developments viz. the formation of the Federal Territories. I also enlarged the text so that smaller thumbnails are legible. Balancing font size, letter spacing and fitting everything in its respective column was quite a challenge! Sadly, MediaWiki has trouble rendering centre-aligned tspan elements on the same line, as can be seen in the Fourier series square wave circles animation.gif animations below, so I had to use uppercase for the place names instead of red text (at least they don't look like links to be clicked).


Greetings from Wikimania 2014!
These plots were inspired by a question User:Alex_Great asked me on my talk page: how to automatically generate random colours for graphs etc. After referring him to http://martin.ankerl.com/2009/12/09/how-to-create-random-colors-programmatically/ , I became curious about low-discrepancy sequences, and learnt about the van der Corput sequence and the equidistribution theorem.
As I was curious about what the sequences look like on a number line, using a visualisation technique User:Timwi had used on the irregularity of distributions article, I wrote a Python script to render the graphs. It's my first attempt at using Python to output SVG (I had previously used Perl). The unexpected result was that of π, which had distinct bands, because milü, the rational number 355/113 is very close to its value.
I also discovered a 2-dimensional version named the Halton sequence, but instead of plotting a graph, which User:Jheald had already done, I decided to show the evolution of the sequence:


I had been reading about the Very Large Telescope, European Extremely Large Telescope and Overwhelmingly Large Telescope (when will they run out of adverbs?!) but couldn't picture how much larger each progressively gets, so I drew this graphic comparing the nominal sizes of the primary mirrors of some large existing and future optical telescopes with various objects like tennis and basketball courts, and the Arecibo radio telescope.
The telescopes are colour-coded by country in which they are located, and whether they currently exist. Their dimensions are as found on the Web, though holes in most mirrors are not shown due to insufficient data. Dotted circles show mirrors with equivalent light-gathering ability.
I'm amazed how enormous the cancelled Overwhelmingly Large Telescope would have been, and conversely, how relatively small the space telescopes (even the JWST). Also note that the hole in the E-ELT is as big as the entire mirror of the largest current telescopes!
SVG-wise, this is my first time using CSS in an original SVG. Quite a neat idea — I must do it more often...
UPDATE 23 SEP 2014: User:71.41.210.146 brought to my attention this very graphic appearing in Gizmodo/Sploid. Cheers!


I recently decided to explore a sometimes-derided type of statistical chart: Pictograms.
Often considered eye-candy, particularly when used where a bar chart is more appropriate, pictograms are usually relegated to infographics in mass media.
I wondered in which use cases pictograms were superior. One example I could think of was where the reader might want to count the number of icons, instead of looking up a scale. This fits well with small discrete numbers, especially where each icon naturally represents a single unit.
To that end, I drew these pictograms, which I think gives a better picture (mind the pun!) of the subject than any other type of chart. Any thoughts?
This video has an excellent visualisation of the effect of taking progressively more terms in a Fourier series. I wish I had seen it when I was learning about Fourier transforms etc, and so, to help future students, I decided to compare four functions using the same technique:
The animations were made by first creating SVGs of their 60 frames and uploading them to Wikimedia Commons to render them into PNGs, which unfortunately centre-aligned the first tspan (instead of the entire row) of each denominator. They were then downloaded, and sliced and combined into GIF animations with these ImageMagick commands:
convert.exe Fourier_series_square_wave_circle_animation.svg.png -crop 1x60@ +repage +adjoin Fourier_series_square_wave_circle_animation_%%03d.pngconvert.exe -delay 10 -loop 0 -page +0+0 ^ Fourier_series_square_wave_circle_animation_000.png ^ Fourier_series_square_wave_circle_animation_001.png ^ Fourier_series_square_wave_circle_animation_002.png ^ Fourier_series_square_wave_circle_animation_003.png ^ Fourier_series_square_wave_circle_animation_004.png ^ Fourier_series_square_wave_circle_animation_005.png ^ Fourier_series_square_wave_circle_animation_006.png ^ Fourier_series_square_wave_circle_animation_007.png ^ Fourier_series_square_wave_circle_animation_008.png ^ Fourier_series_square_wave_circle_animation_009.png ^ Fourier_series_square_wave_circle_animation_010.png ^ Fourier_series_square_wave_circle_animation_011.png ^ Fourier_series_square_wave_circle_animation_012.png ^ Fourier_series_square_wave_circle_animation_013.png ^ Fourier_series_square_wave_circle_animation_014.png ^ Fourier_series_square_wave_circle_animation_015.png ^ Fourier_series_square_wave_circle_animation_016.png ^ Fourier_series_square_wave_circle_animation_017.png ^ Fourier_series_square_wave_circle_animation_018.png ^ Fourier_series_square_wave_circle_animation_019.png ^ Fourier_series_square_wave_circle_animation_020.png ^ Fourier_series_square_wave_circle_animation_021.png ^ Fourier_series_square_wave_circle_animation_022.png ^ Fourier_series_square_wave_circle_animation_023.png ^ Fourier_series_square_wave_circle_animation_024.png ^ Fourier_series_square_wave_circle_animation_025.png ^ Fourier_series_square_wave_circle_animation_026.png ^ Fourier_series_square_wave_circle_animation_027.png ^ Fourier_series_square_wave_circle_animation_028.png ^ Fourier_series_square_wave_circle_animation_029.png ^ Fourier_series_square_wave_circle_animation_030.png ^ Fourier_series_square_wave_circle_animation_031.png ^ Fourier_series_square_wave_circle_animation_032.png ^ Fourier_series_square_wave_circle_animation_033.png ^ Fourier_series_square_wave_circle_animation_034.png ^ Fourier_series_square_wave_circle_animation_035.png ^ Fourier_series_square_wave_circle_animation_036.png ^ Fourier_series_square_wave_circle_animation_037.png ^ Fourier_series_square_wave_circle_animation_038.png ^ Fourier_series_square_wave_circle_animation_039.png ^ Fourier_series_square_wave_circle_animation_040.png ^ Fourier_series_square_wave_circle_animation_041.png ^ Fourier_series_square_wave_circle_animation_042.png ^ Fourier_series_square_wave_circle_animation_043.png ^ Fourier_series_square_wave_circle_animation_044.png ^ Fourier_series_square_wave_circle_animation_045.png ^ Fourier_series_square_wave_circle_animation_046.png ^ Fourier_series_square_wave_circle_animation_047.png ^ Fourier_series_square_wave_circle_animation_048.png ^ Fourier_series_square_wave_circle_animation_049.png ^ Fourier_series_square_wave_circle_animation_050.png ^ Fourier_series_square_wave_circle_animation_051.png ^ Fourier_series_square_wave_circle_animation_052.png ^ Fourier_series_square_wave_circle_animation_053.png ^ Fourier_series_square_wave_circle_animation_054.png ^ Fourier_series_square_wave_circle_animation_055.png ^ Fourier_series_square_wave_circle_animation_056.png ^ Fourier_series_square_wave_circle_animation_057.png ^ Fourier_series_square_wave_circle_animation_058.png ^ Fourier_series_square_wave_circle_animation_059.png ^ -coalesce -depth 3 -colors 32 -dither FloydSteinberg Fourier_series_square_wave_circle_animation.gif
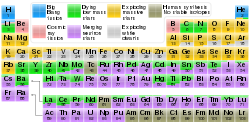
As Neil deGrasse Tyson movingly put it [3], an astounding fact is that we are star dust — most of the elements in our bodies (barring some recent radioactive-decay products) were created in stars, by cosmic rays or during the Big Bang itself.
At a talk at the Cambridge Institute of Astronomy, the speaker presented a slide similar to this periodic table showing the origins of the elements. I was surprised to find Wikipedia without an equivalent graphic, so decided to make one!

The SVG itself is straightforward, the only interesting bit being the Appley skeuomorphic gradient shading I "invented" when making the Git chart on the left:
Applying this to a shape makes its top 10% half-transparent white, and its bottom 10% black but fully transparent. The middle region has a curious gradient which, in my opinion, looks quite attractive when overlaid on a copy of the shape filled with the intended solid colour.

I caught Gravity on a flight and marvelled at the amazing special effects and way-above-average accuracy of its portrayal of space travel, particularly how the alarm sounds came back when the hallucination turned up the air pressure and how the Soyuz righted itself during reentry.
Nevertheless, one of the popular gripes is how easy it was to travel between the Hubble, ISS and Tiangong. Of course, one could imagine an alternate universe where they are put into almost identical orbits. When the film first came out, I drew this graphic to show how different the real ISS and Hubble's orbits are. Even if they were at the same height and almost the same longitude/latitude, their orbital inclinations would require huge change in delta-v which I doubt a backpack could provide.
As for the creation of the image, I faced the classic problem of "drawing Saturn with its rings": How to draw a circle with an ellipse both behind and in front of it?
The solution I used was to erase half the ellipse using an SVG clip-mask, and draw it over the globe which already has the full ellipse drawn under it. Because of anti-aliasing, the twice-drawn half is slightly thicker than the other half, but it's not noticeable at normal resolutions. I could have made the ellipse below also a half-ellipse but thought that any gap in the joint would look even worse...
This dimetric projection of the tallest building in the world is my first SVG animated using CSS3. I had previously used JavaScript/ECMAScript to animate SVG but the Wikimedia uploader rejected it as JavaScript was considered a security risk. Using CSS3 is more limited, allowing noninteractive animation of various attributes, the transform attribute in this case.
Using the technique to simulate 3D rotation below, I rotated each different floor plan, replicated it in the appropriate colour as many times as needed, and scaled the whole group vertically by half. The illusion was reinforced by the sheer number of floors. The only niggles were...

I was so satisfied that I retroactively applied it to the Absolute World Tower model and was even more impressed with the quality of the rendering. As there were fewer elements and the floors were more rounded, both the animation and the silhouette were much smoother. That the Mediawiki renderer ignores CSS3 was used to show the rightmost text label only in a static thumbnail.
Sadly, browser support for CSS3 is still patchy: the test animation of falling snowflakes works in Chrome, but not in Firefox 26.0. At time of writing, noone has suggested a fix or workaround for this bug :-(
Incidentally, it's now been 2 years since I started this behind-the-scene look at my work with Wikipedia/Wikimedia. Does anyone actually look at this? If so, I'd love to hear from you — cheers!
UPDATE 26 JAN 2016: user:RaphaelRBarbosa reminded me that the snowflakes animation now works in Firefox — thanks, Raphael!

I play a game which has characters making various sculptures, each attempt generating 1 of 12 possible sculptures at random. Every time I complete a "collection" of 12, I get a bonus and get to start a new collection.
I wondered how many tries I need, on average, to complete a collection from scratch. A search introduced me to the Coupon collector's problem. Paraphrasing the article,
The answer uses a series which I had read about but never known an application for: the Harmonic series, in the form
Mathematical induction gives E (T ) = n Hn , which I've plotted for n from 1 to 60 (to cover the case of 52 playing cards — I'd have preferred 100, but that makes the smaller bars too hard to see).
I added dotted lines to show the number of tries needed for each coupon. Though this value increases, it increases rather slowly, as E (T ) being linearly proportional to n logn implies.
Back to my game, my 12 sculptures would thus require 38 attempts, on average. In practice, I found that it takes fewer tries, perhaps because it wasn't as random as I'd thought.
By the way, I love the elegant proof that the harmonic series diverges (goes to infinity as n approaches infinity), unlike a geometric series with a ratio between -1 and 1 (not inclusive). I'll consider drawing a proof without words of it one day...


I used to be baffled by photographs like the one of the helicopter on the left, wondering what on Earth could have caused such distortion on the blades! I recently learnt that it is an effect of the rolling shutter on many digital cameras, especially those on mobile phones.
Unlike film cameras which expose the entire frame at the same time (actually they have rolling blinds too, but the effect is only apparent at very fast shutter speeds), cameras without a mechanical shutter expose and read off a line at a time. This means that by the time the last row is captured, a fast-moving subject will have moved significantly from where it was when the first row was captured.
To illustrate the warping more precisely, I came up with a sequence of 24 frames of a rotating disc and simulated a rolling shutter scanning a row at a time. In each frame, the left half shows the state of the disc and the position of the captured row, while the right half shows the image captured until that point. Sadly, there is a bug in Mediawiki (not in Firefox or Chrome) that renders some artifacts in the top rows; I guess it didn't like my 24 levels of nesting to generate the captured image sequence, the most I've used to date.
Nevertheless, it's now clear to me that the part of the disc moving in the direction of the scan (the right side) is smeared out into large shapes while those moving the other way (the left side) is compressed. The small number of rows cause the jagged appearance; more rows in a real camera lead to smoother curves.
To complete the simulation, I sliced the image into 24 layers in Gimp and stitched them into GIF animation.
I later found this video which explains it even better. I might make a similar animation in the future...
UPDATE 31 MAR 2014: Really proud to see my animation not only used on Vsauce, but host Michael Stevens even built on it to explain that our view of the Andromeda Galaxy suffers from a rolling-shutter effect.
File:Hipparcos_Catalogue_equirectangular_plot.svg marked the completion of my trio of charts of objects in the night sky, all of right ascension against declination in an equirectangular grid:

Another year, another Open House London!
This time, I managed to win the ballot for a place on the Arriva Heritage Bus Tour, which used the last classic Routemaster, RM2217 to take us to 5 landmarks:
I also visited the Foreign and Commonwealth Office (FCO), and the Brunel Museum and its recently-reopened entrance shaft of the Thames Tunnel.
Of course, my trusty camera came along, so here's another batch of photos for your viewing pleasure...

Today, I got my first Wikimedia request for a logo design (a very old hobby) for the so-called Million Award, which I think is a good idea — much as I enjoy drawing pretty pictures of my interests, I've long thought that my efforts benefit society most when spent on popular topics which are somehow lacking.
The requester, User:Khazar2 had adapted my visualization of 1 million graphic (see below), so I continued in that direction. Befitting the theme of "million", the middle cube has 1 millionth the virtual volume of the large cube, while the CMYK colours evoke the idea of "articles" in the traditional printing sense. "1M" is hopefully language-independent and the star is a common motif for awards such as the Barnstar.
The skewed text is also my first use of SVG matrix affine transformation, and I was delighted that the bottom-right edge of the star (simply Unicode character U+272A) lined up with the bottom-right side of the cube. It was also my first attempt to specify a particular font, in this case, one with tapering (not slab) serifs so that the "1" and "M" look more elegant and reminiscent of printed text.
All in all, it was a fun little project for the day!
I revisited the Horniman Museum, one of my favourite museums in London because of their approach to education by comparing artifacts from different cultures. I also love their skeleton-skin preparations, which show just the skeleton in half of a stuffed animal, as it shows how the bones (and consequently, muscles and internal organs) fit in the body. These are some examples:
I also reshot the London skyline from Forest Hill to show a completed Shard. Sadly, the summer air was quite hazy, but some image-processing helped. In the style of Horniman, see how the city has changed in 1½ years!
More photos are at Commons

The Laboratory of Molecular Biology opened its doors to the public on Sat, 22 June, so my friends and I attended some talks, exhibitions and a tour of their new home. (I also used the opportunity to take some photos!)
One of the speakers talked about a mutation causing possibly the greatest cancer risk in the world: ALDH2*2
With China rapidly adopting a drinking culture, about 25% of the East Asians (perhaps 300 million people) face increased risk of esophageal cancer. If I understood correctly, the risk of an affected person drinking, compared to an unaffected one, is greater than that of lung cancer from smoking (of course, the quantity matters...)
I couldn't find a graphic of the breakdown of alcohol in the alcohol flush reaction page, so tried to create one. I could have done it in SVG, but thought it was an interesting experiment to do it in the LATEX-like maths "equation editor". I had to tweak the spacing quite a bit and couldn't draw diagonal double bonds, but managed the following:
Whatjsay? :-)

Timwi's image at http://imgur.com/gallery/eUMMCtb got me interested in calendars again — I must be getting old!
His most amazing find was that the 400-year cycle of the Gregorian calendar (the one in everyday use today) has a multiple of 7 days, meaning that the cycle repeats exactly every 400 years. But interesting and colourful as his graphic was, it didn't help with my understanding of how the 14 possible calendars actually change, so I decided to draw my own...
While on holiday, I wrote a quick program to output into a simple text file as one line separated by spaces:
Changing the width of my text editor window let me see in how many years the pattern more-or-less repeated.
The answer was 28, not surprisingly the lowest common multiple of 7 (days in a week) and 4 (almost every 4th year is leap), the pattern disrupted only by the non-leap years 2100, 2200 and 2300. 28 columns would, however, be too wide, so I decided to go down then across, instead of across then down.
The pattern appeared more regular now, but the non-leap century years still played havoc, until I got the idea of skipping the necessary number of cells until the pattern resumed. There are actually 2 possible places each non-leap century year can go. I chose the later one so that 2300 doesn't end up at the top of its column.
This resulted in the graphic on the right. It's now much clearer to me how the calendars cycle — one day forward each non-leap year, and two days forward each leap year, except for the non-leap century years which leave large gaps.
P.S. I redrew the graphic in Wikitext below, if anyone wants an HTML copy.

Once again, I'm honoured to see this cartogram of the parliamentary constituency results of the Malaysian general election, 2013 appearing on the main page of the Chinese Wikipedia.
To be honest, most of the credit should go to User:Hytar who made the cartogram for the Malaysian general election, 2008. I just fixed a few minor cosmetic issues, tidied up the SVG code and updated the data to reflect the 2013 results. Due to his or her judicious use of CSS, the task was pretty straightforward.
I must give kudos to Hytar, too, for being so supportive and polite — a model Wikipedian if there was one!
The next job is to update File:Dewan_Undangan_Negeri_2008_Equal_Area.svg with this year's results. Hytar referred to some spreadsheets going around. Obtaining one would make updating the 505 hexagons much easier.
{{Blakey_65moll.jpg_K/T_impact_site}}Today, I discovered a new technique to annotate images, using the Annotated image template. I had previously converted bitmaps to Base64 and embedded them in SVG files. With the template, I could add labels to any image directly in the Wiki markup.
For example, the code below produces the graphic on the right. The template also let me crop the sides of the Mollweide projection, to make the graphic fit inside text and yet allow detail on the map to be clearly seen. To isolate the label from the bitmap, I repeated it twice in black with slight offsets to simulate an outline — an alternative was to use a CSS shadow but CSS support for it is dicey.
I was surprised to find plenty of maps of the Chicxulub crater, the location of the Cretaceous–Paleogene_extinction_event, but no world maps showing this location on Wikimedia. Of course, the world looked a bit different 65 million years ago!
{{ Annotated image | image = | caption = K/T impact site on a contemporary world map (65 mya)<ref>[http://www.scotese.com/K/t.htm K/T extinction]</ref> | width = 300 | height = 190 | image-width = 400 | image-left = -45 | image-top = -3 | annotations = {{Annotation|74|64|* Impact site|font-weight=bold|color=black}} {{Annotation|76|66|* Impact site|font-weight=bold|color=black}} {{Annotation|75|65|* Impact site|font-weight=bold|color=white}}}}UPDATE 26 JAN 2016: It seems the maps have been removed due to copyright violation; I'll see if I can redraw them in the future.

Ever since I learnt about the differential pulley, I have been intrigued by the mechanism. Although it superficially resembles a block and tackle, at least two of its pulleys are sprockets, which engage with a chain, hence its other name, "chain hoist". Additionally, these two pulleys are joined together, and the ratio of their diameters (or radii) determines its mechanical advantage.
Drawing a graphic of it was an interesting exercise in SVG-hacking:
First, the teeth of the sprockets were simply the dotted stroke (outline) of the circle representing the pulley, set to the same colour as its fill, and with the duty cycle, phase and width adjusted to fit.
Next, I needed a path that looked like a chain, and found a way to do it with three dashed lines of different duty cycles, phases, widths and colours, one of them in the background colour to "erase" the hole in the links. This looked fine until I overlaid the chain on the pulleys, making the background colour incorrectly appear over the pulleys. If only clip paths had an inverse function which let one ignore pixels inside the path, rather than outside!
I left the problem for over a year before discovering masks. I could now draw the chain without the holes and overlay the whole thing on any background. The experiment on the left, a world map with borders replaced with chains, proved that this technique was feasible as long as turns were not too sharp. The hack was successfully applied to the differential pulley graphic (right), though I later found that Google Chrome had trouble with my mask. Oh well...
UPDATE 20 AUG 2019: While showing it to Deryck Chan on the NYO airport bus to Wikimania ’19, I remembered two bugs:
and fixed them en route back to Cambridge.


I met User:Charles Matthews, User:Deryck Chan and User:Magnus Manske at the Cambridge Wikimedia Meetup Number 17 again yesterday and they convinced me that artwork from 1850 and before is globally considered public domain. I've therefore completed upload of 50 historical paintings and drawings of Penang housed in the Penang Museum and Art Gallery. The works show a much quieter island compared to the bustling city of today, but likely presents a European colonist's romanticised perspective. Nevertheless, it serves as a good historical record of the island.
There are 11 other pieces dating from after 1850, and 2 with dates unstated. Perhaps someone can upload them as they come out of copyright in the coming years...

UPDATE 9 SEP 2018: After reading through commons:Commons:Village_pump/Copyright/Archive/2017/03#Cut-off_date_for_the_PD-old_template, I decided it safe to upload all but the last three paintings (1876 is 142 years ago – longer than the most conservative 140 years proposed – but 1924 is only 94)


As several Asian cultures celebrate the lunar new year tomorrow, I made a couple of somewhat related illustrations.
I have sometimes wondered how the Chinese decide that a particular year is the Year of the Water Snake (for example). I knew that the 12 animals of the Chinese zodiac go in sequence but the element was a mystery. The Sexagenary cycle article makes it clear: The element cycles in the order wood, fire, earth, metal and water, changing every two years (the first year being yang and the second, yin). With that in mind, I drew the graphic on the right, adding in the numeric years. As it wasn't immediately obvious, I also added a tortuous line to show the progression — hope it's not too messy... I initially laid the years out in a table before realising that they wrap around in both X and Y axes: The surface of a toroid! Alas, drawing a toroidal surface isn't that easy, so the best I could manage was to make an annulus (mathematics) and wrapping the element radially.
The graphic on the left is based on a clever optical illusion which tricks the brain into seeing movement where there is none. The original, named Rotating Snakes, by psychologist Kitaoka Akiyoshi is an example of peripheral drift illusion which works on the viewer's peripheral vision. For best effect, one should use as large an image as possible, such as this one. An even more stunning illusion is found on the cover of the indie album Merriweather Post Pavilion.
Happy lunar new year to all who celebrate it!
I've just updated my comparison of some pyramidal buildings, adding the collapsed pyramid at Meidum to replace the Bosnian "Pyramid of the Sun" which was forcefully removed due to the misconception that I had tried to promote the Bosnian hill as a building. That was never my intention — I thought that including it in the graphic only served to highlight how ridiculously enormous it was compared to other pyramids. Nevertheless, an editor removed it, leaving an unsightly gap in the labels.
Meanwhile, I had been thinking about including the Meidum pyramid but felt that my SVG skills were inadequate at the time. Now that I had more experience with Bézier curves and a gap to fill, I traced this illustration and added it to the graphic, renumbering the pyramids in the process (I had checked that no pages that used it referred to the numbers).
Guess you can't win every battle, but you can make the most of the outcome!
UPDATE 16 NOV 2014: I've hyperlinked the label and profile of each "pyramid" so that hovering highlights them and clicking opens its Wikipedia article.
Today marks the Perihelion of the Earth, the moment in a year that the Earth is closest to the Sun, paradoxically near the coldest time of year in the Northern Hemisphere!
A while back, I discovered the ability to render graphics in an article by just writing some code, instead of uploading an image (such as SVG) and transcluding it: EasyTimeline.
Originally designed to create timelines, it can be repurposed to draw bar charts in general. My first use of it is the chart below graphically illustrating the range of distances some bodies of the solar system can be from the Sun. It can be seen that the inner planets have almost circular orbits whereas the outer dwarf planets and Halley's Comet have very eccentric orbits.


I'm pleasantly suprised at the lack of media coverage of the 2012 phenomenon, considering the frenzy when the 2012 movie was released — it's certainly nothing like what accompanied the Y2K scare.
Nevertheless, I was curious to find out the relevance of today's date in the Mayan calendar and read about their units of time. 21st December 2012 marks the end of the 13th (written 12 in their dates as they start counting at zero), and the start of the 14th b'ak'tun, a unit of time 144000 days long (around 400 years).
Using the idea I developed to visualise largish numbers at the same scale (one million in the illustration on the right, and one billion in this one for high-resolution screens), I drew similar blocks representing the Mesoamerican time units up to a piktun (around 8000 years), in principle representing almost 3 million small cubes in the largest block! I added colours and a scale showing equivalent dates on the Western calendar. To reduce the width of the image, I flipped my trimetric projection horizontally.
From this image, I can see that while the date is interesting, it's not exceptional as it occurs once every 394 years. Moreover, nothing major happened at the last few changeovers: 1618, 1224 and 830.
On that note, I'll just wish everyone, "Happy new b'ak'tun!"
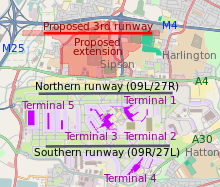

The map on the left is my first attempt to combine an SVG export of OpenStreetMap data with annotation to show the terminals of London Heathrow Airport and its proposed extension, although I had previously embedded bitmaps of OpenStreetMap maps in the illustration of the Fukushima Daiichi nuclear disaster (right).
Though I have used Heathrow Airport for many years, I had no idea about its layout, other than the Central Bus Station and Underground station serving Terminals 1 and 3 (and formerly Terminal 2) while Terminal 4 had its own stations. The map now makes it clear how the buildings are laid out with respect to the runways and one another. I took the opportunity to illustrate the controversial third runway and extension, which has garnered plenty of press coverage in the UK.
Technical-wise, I found adding annotations straightforward but modifying existing SVG objects (even just changing their colours) quite difficult, particularly since there were so many objects that I had to hunt down the target object by colour, which was specified as, for instance, rgb(80%,60%,100%) instead of the more common #cc99ff format. I also thought the SVG was extremely inefficient in terms of file size. I would have, for example, grouped all objects of the same style and applied the styling to the group, rather than style each object individually. If I ever need to annotate an exported OpenStreetMap SVG again, I'll consider using an editor like Inkscape.
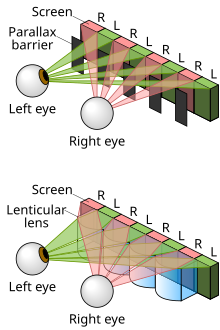
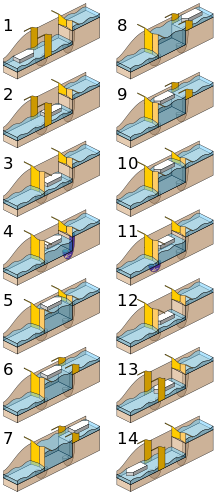
Another thing that we talked about at the CUWPS gathering was three-dimensional (3D) displays, such as those in the Nintendo 3DS. I showed the group the drawing on the left to illustrate the principle, and the subject changed to drawing SVG.
We looked at the source code and discussed use of groups, transforms and defined blocks to reduce the effort of producing one, while also saving on file size.
This drawing is one of my forays into simulating a 3D scene in a 2D medium, ironic considering the subject of the drawing is technology to simulate 3D with 2D!
The projection used is the approximate isometric projection used in isometric graphics in video games and pixel art, actually a dimetric projection. It simplifies mapping between 3D and 2D coordinates in this case, so I could work out the coordinates by hand, but traditionally, it allowed pixels to fall neatly into the raster graphics matrix without needing antialiasing. It looks slightly more aesthetic than true isometric to me, too, as more of the sides is visible than the top, just like how I would sketch a 3D object.
Another drawing done with the same projection is the sequence on the right is showing how some canal locks work.


I have always been interested in the small island of Penang and was over the moon when I found this scan (left) of an ancient map dating from 1799. Though it was only 13 years since Penang's founding, the map had landmarks such as Fort Cornwallis, Penang Road and the grid of streets near Beach Street. It was fascinating that while land to the southeast had been reclaimed to build Weld Quay, land to the north had been lost to the sea, which may explain why the Esplanade was built.
It then occurred to me that Penang being a British colony meant that there must be extensive historical records of early Penang within a stone's throw at the Cambridge University Library. I found that very book from which the 1799 map came, and also a more recent map in the Map Room (right) — how Penang had grown in 85 years!
I spoke of my experience with the Cambridge University Wikipedia Society at their gathering yesterday and discussed with President Deryck about expanding GLAM to include the University Library archives. I know I'd certainly be interested in their ancient maps ୯ ͡° ͜১͡° ੭

I attended the 16th Cambridge Wikimedia meetup and inaugural Cambridge University Wikipedia Society meeting yesterday and had the pleasure of meeting several enthusiastic Wikimedians/Wikipedians and learning about the projects and ideas of User:Charles Matthews and User:Magnus Manske. I'm looking forward to the planned collaboration with the University of Cambridge and local museums.
Speaking of Cambridge University, on the right is a chart I made a while ago to illustrate the complex history of the colleges of the University of Cambridge. It shows the years of formation of the colleges, when they changed their names, and most importantly, when they started admitting women (or men, in the case of Girton College and Hughes Hall). Obtaining all this data from disparate sources was quite a challenge, and I'm still missing one crucial date:
When St Edmund's College became mixed.
Repeated emails to various parties in the college were unanswered, so I've shaded the transition to the range of years this could have happened. Anyone got any idea?
UPDATE 28 NOV 2012: User:Deryck Chan managed to get a statement from St Edmund's Emeritus Fellow Dr Michael A Hoskin that he remembered it as 1969. Pending confirmation of historical records, I've tentatively indicated 1969 as the year St Edmund's became mixed.
UPDATE 17 DEC 2012: Thanks to the tireless effort by the St Edmund's College Combination Room Women’s Officer, Miss Maryam Farooq, the year women could be admitted to St Edmund's College, as postgrads, has been established to be 1965.



Last weekend, hundreds of establishments in London welcomed visitors for Open House London, and so I took the opportunity to visit a pioneering work of shipping container architecture at Trinity Buoy Wharf: Container City.
The structure consists of two buildings named Container City I and Container City II, made out of 52 old 40-foot shipping containers. Even the lift shaft and stairwell are containers standing on end. I really like the balconies made from the containers' open doors, and the bright colours.
Unlike the exterior, its interior looks pretty much like ordinary flats except for the portholes and occasional glimpses of the exterior, and tall people may find the low ceiling claustrophobic! Being an open house, a studio was open to the public, though I cynically think it's just a ploy to get people to rent it :-)
To better understand its structure, I reused my patented (not!) trimetric projection to depict the containers, one layer at a time. The SVG code was wholly done in Notepad++, believe it or not, though the hardest part was finding out what colour each container was painted!

Continuing the theme of clock faces, I recently found out about a method scouts and similar groups learn to locate north and south using the sun and an analogue clock or watch:
As the sun appears to complete one rotation around the sky in 24 hours while the hour hand of a 12-hour clock takes 12 hours, bisecting the angle lets one identify the cardinal directions.
Unfortunately, modern timekeeping complicates matters with time zones and daylight saving. Most countries (except perhaps China and Kiribati) have time zones roughly corresponding to the local time. Daylight saving normally move clocks forward by an hour.
Using this information, the more detailed description at Cardinal_direction#Watch_face and the infamous marketing time, I illustrated these four scenarios:
The SVG itself is rather straightforward, the only difficulty being calculating the rotational transforms. What I'm a little proud of, though, is the sun rendered with 8 quadratic Bezier curves and a radial gradient!


I had read about the Abraj Al-Bait Towers (left) and was curious to know how large its new-world-record clock actually was. The statistics, such as its 46-metre-diameter clock faces don't really do it justice, so I decided to create a photomontage of notable four-face clocks and clock towers, all at the same scale.
I chose the Allan-Bradley (the previous record-holder), Big Ben clock tower and Met Life Tower clocks, and later added the Kremlin one, as I felt that they gave a fair representation of famous large four-face clocks.

Next was sourcing photographs of these clocks. I used the crop tool in Photoshop to orthorectify them, so that they appear like they were taken head-on. This process was simplified by the fact that the faces were nearly two-dimensional and I could assume that they were circular. I had had recent practice orthorectifying images, such as one of The Great Picture on the left.
I then had to find a way to get all the images to the same scale. Using the more common "diameter of dial" was troublesome, as the extent of the dial varied from clock to clock. Instead, I used the published lengths of their minute hands as it is easy to measure and one of the longest measurements specified, to reduce uncertainties.
Composite the montage, write a caption, create a template to present it uniformly, and that was basically it...
Now one can see how enormous the new clock is; the entire Big Ben clock tower (to be named the Elizabeth Tower for the British Queen's 60th year at the throne) could fit in the Abraj Al-Bait spire, and if the new clock had numbers on the dial (it has ticks), each number would be almost as big as one Big Ben clock!

I met an architect who is a fan of Santiago Calatrava and we started talking about his Turning Torso. I found it difficult to visualise its shape, especially because most photograph show only the view taken from the ground (far left).
A little Googling later uncovered plans at http://www.calatrava.info/imageViewer/turningtorso/stor_plan.gif and http://blogfiles7.naver.net/data19/2006/10/27/22/Turning_Torso_Plans-43rd_Floor_1-jinsub0707.jpg .
With a trick I learnt from Adobe Flash to simulate 3D shapes with 2D ones (rotate then scale horizonatally and vertically by different amounts, and rotate again if needed), I drew this illustration (near left). I can now see the building's shape much more clearly! By the way, guess what influenced the choice of colours...
UPDATE 10 MARCH 2013: The idea was reused for the illustration of Absolute World on the right.

I had wondered how to draw the intersection of two SVG shapes, such as the purple areas in the image on the right. One simple method is to set the opacity of the upper (drawn later) shape between 0 and 1, to make it semitransparent. However, this also causes the non-overlapping area to be semi-transparent.
It occurred to me that I could draw that shape twice. Calling the shapes A and B, we can draw A and then B fully opaque, and finally draw a semitransparent version of A on top. The opaque A ensures that the non-overlapping areas remain opaque. In theory, this is slightly different from a single opaque A due to anti-aliasing at its edges, but I haven't found any problems in practice.
The same idea was used in the graphic comparing convolution and correlation functions on two signals. This image additionally uses a more advanced technique with clip paths to shade the common areas under the graphs, but a description of it will have to wait until another day...

I've just discovered a way to embed the name of the current page in a transcluded template, using the {{PAGENAME}} system variable.
For example, the caption of the image on the right should read, "Location of Cmglee in the Indus Valley and extent of Indus Valley Civilization (green)." (unless someone has changed the template!)
Of course, that doesn't make much sense! That's because the name of this page is Cmglee (its full name being User:Cmglee).
When the CiviltàValleIndoMappa-en template is used in the articles for the cities labelled, such as Mohenjo-daro and Harappa, it does its magic. For instance, in the Mohenjo-daro article, the caption reads, "Location of Mohenjo-daro in the Indus Valley and extent of Indus Valley Civilization (green)."
This allows the same image with an appropriate caption to be placed in multiple articles without having to copy and paste the same wikitext and then amend the city name in all of these pages. Moreover, updating the template instantly updates all pages using it. Nice!


One of the frustrating limitations of SVG is the lack of a feature to automatically draw a smooth curve through a set of points. Sure, one can draw Bézier curves and elliptical arcs between pairs of points, but the coordinates of control points or arc radii must be specified.
Based on an algorithm at Stack Overflow, I developed a Perl function to automatically calculate the control points of cubic Bezier splines to smooth a polyline.
Each point (except the end points) can take up to two curviness values which determine how curvy or straight the curve on each side of the point is. Zero curviness results in a simple polyline. Applied to individual points, this can be used to create sharp corners. Negative curviness is used to create loops. The test curves on the left illustrate its use.
One of the first applications of this function (adapted to gradually change the colour of the curve along its length) is the creation of the simplified torch relay route map to the right. The actual route is far more tortuous than this. To make it easy to trace at this scale, I just wanted the curve to smoothly pass through all the marked places. To make crossings clearer, the curviness of certain points were tweaked until visually acceptable.
Another application, which I shall use more often as the need arises, is the drawing of the smooth curve of many mathematical functions. Currently, I have to generate hundreds of points to get a reasonably smooth curve. With this function, far fewer points will be required.

I was pleasantly surprised and honoured to see my photograph of ArcelorMittal Orbit appearing on the Wikipedia main page on 17 May.
It was almost an accident that I shot this photo. On that fateful day, I had taken a coach from Cambridge to London to catch a London Prepares test event at the Olympic Park. I had expected to alight at Stratford, as I had done several times before. I was aghast that National Express had changed the 010 coach schedule to bypass Stratford, forcing me to get off at Bow and walk back to Stratford.
I remembered a great view of the Olympic Stadium and Orbit visible from the flyover above the A118 roundabout — I had uploaded a much lower-quality version of the same scene from a coach to London a few months before, as can be seen from the file's history. So, I decided to climb it.
Though there were no signs forbidding pedestrian entry, the overpass was mighty hairy, with nary a footpath to avoid the fast-moving traffic. Nevertheless, I was rewarded with this magnificent view — if you could call the Orbit "magnificent" ;-)
And that's the story behind the picture... Keep tuning in for more behind-the-scenes!


This BBC News article reminded me of the graphic on the right, which I made to compare the life expectancies (at birth) of males and females in different countries. As is widely known, women generally outlive men, particularly in the Eastern European countries labelled. The BBC article discusses possible reasons for this. There is, however, a reversal of this trend in sub-Saharan Africa. It is even more extreme in Montserrat, where (if the figures are to be believed), men live a whole 3¾ years longer than women, on average.
I initially found it a challenge to depict the size of the countries' populations, ranging from about 5000 to almost 7 billion. I could have used a logarithmic scale, but decided to imagine the markers as 3-dimensional "bubbles" with volumes proportional to their population. That let me cover the 6 orders of magnitude with radii covering 2 orders of magnitude, so that if, for example, the smallest bubble were 1 pixel wide, the largest would be a manageable 100 pixels wide.
Additionally, the transparent bubbles let multiple bubbles overlap and still be visible. A small dot at their centres allow the reader to read off the life expectancies in years.
The same idea was reused for the graphic on the left, showing fatalities in earthquakes of magnitude 8 and greater since 1900.

A recent exchange I had with RacerX11 reminded me of the benefits of constructive cooperative editing.
I (and presumably some others) have wondered how the famous tall mountains around the world, such as Aconcagua and Kilimanjaro compare with the giants of the Himalayas. Of course, I could look up their heights to the metre in various tables, but there's nothing like a scale image to provide instant understanding, as in the comparison of skyscrapers on the left.
So I decided the compare the Eight-thousanders, Seven Summits and Seven Second Summits in the top-right graphic. Sadly, I had to use triangles as I did not have the actual elevation profiles of the mountains.
Neither RacerX11 nor I were satisfied with my use of symbols to show which list each mountain belonged to. There were actually 5 lists:
After throwing ideas at each other, I realised that I could group their labels as in the bottom-right graphic. RacerX11's finishing touch was to use symbols to distinguish just the 4 mountains in the Bass and Messner lists.
It would have been superb to add the Volcanic Seven Summits and Volcanic Seven Second Summits, too, but the image was already a bit cluttered, and there is controversy on the membership of the list itself.
UPDATE 31 JAN 2013: I just found out that Thomas Laussermair has written on http://visualign.wordpress.com/2012/06/04/graphic-comparing-highest-mountains/ very kind words about the image and a mod I made for him — thanks, tlausser/visualign!
I borrowed a Fujifilm FinePix Real 3D W3 and went around taking photos of Cambridge in the summer of 2011.
I then developed the stereoscopic image template to let the reader view the pictures in various arrangements — though cross-eye viewing lets one view much larger images, some people find parallel viewing more comfortable. The template supports side-by-side sterescopic images in both parallel and cross-eye formats.
The first stereoscopic photograph I've uploaded to Wikimedia shows a Stagecoach Citi 1 bus in King's Hedges, a residential suburb to the north of Cambridge city centre.

Being a markup language, SVG code can be easily generated using a program or script, as contrasted with, say, a Microsoft PowerPoint or Adobe Illustrator drawing.
As I'm already familiar with Perl (the less-abstruse constructs, at least!) I wrote scripts to automatically generate SVG code which would otherwise need lots of calculator work, such as drawing graphs. Labels and other decoration can then be manually added to complete the illustration. So that a future editor can easily tweak the code, the Perl code appends itself to the SVG as a comment.
An example is this diagram which shows how a projectile behaves when launched at different angles of elevation, in the absence of air resistance.
As is often taught in high school, a 45° angle indeed gives the greatest range. What is less known is that the time of flight increases with the angle. Since there are two complementary angles giving the same range (other than the maximum), it is possible for artillery to fire a shell at the larger angle, then another at the smaller one after an appropriate delay, so that both shells hit the target at the same time — a basic form of Multiple Rounds Simultaneous Impact.
One of the features of SVG which initially attracted me was the ability to embed a bitmap, such as a JPEG or PNG image.
This allows labels to be relatively easily updated or translated into different languages, by simply replacing the English terms in its SVG file with a text editor, as Timwi has done with the lower image on the right.

Before I learnt this, I had to tediously edit the image on the left to correct "sea of storms" to "sea of crises" (unable to find a matching font, I manually cut and pasted individual letters from other labels).
Even after doing so, saving the file slightly reduced the image quality, due to the lossy compression JPEG uses.
UPDATE 31 JAN 2013: http://www.motobit.com/util/base64-decoder-encoder.asp provides a useful facility to convert an image to Base64 which can then be embedded in an SVG as follows (replace png with jpeg, gif etc as needed):
I had once toyed with the POV-Ray raytracer. Similar to SVG, one writes code to render an image, but in this case in 3D!
As I thought that the tensegrity article could benefit from an animation to better show the spatial relationship of structural parts, I decided to create a GIF animation of a rotating structure, as on the left.
Alas, a reader found the animation distracting, so we settled on a static image with a link to the animation. It then occurred to me to use the stereoscopic image template I had once written to display the static image, as on the right...

Following the success of Derby Backstage Pass, the UK chapter of the Wikimedia Foundation and Herbert Art Gallery and Museum, Coventry organised Herbert Backstage Pass on 1 October 2011. The first major Wikipedia-related event I've attended, it seemed a perfect collaboration: The museum giving Wikimedia members access to parts not normally accessible to the public as well as time and attention of curators and other staff, while the members contribute to Wikipedia articles relevant to the collection.
This photograph (right) was taken at the end of the day, sadly after several attendees had left. More photos of the event can be viewed here.

UPDATE 15 OCTOBER 2013: My visit to the Coventry Transport Museum to see ThrustSSC on that Coventry trip has just resulted in my third (as far as I can tell) image to appear on the Wikipedia main page (today's). ☻✌

This image marked the start of my regular contribution of SVG drawings to Wikipedia. I found using SVG to mark up images (especially by hand or with a script) rather fascinating, albeit at times frustrating due to
Making this image taught me various SVG basics, such as setting the viewport, creating and transforming primitives, and using defined blocks. A trick I found is how to properly outline overlapping shapes with semi-transparent fills (the naive method causes strokes (outlines) to be overlaid, giving outlines of inconsistent colour):
El diagrama de Venn en sí mismo es una solución estética al problema de cómo representar, con sólo elipses, todas las combinaciones posibles de cinco conjuntos, apareciendo cada combinación exactamente una vez. [3]
¿Aún tienes el código que usaste para generar el diagrama de Venn de 5 vías? Me gustaría saber el centro de la elipsis, por eso pregunto. Gracias. Carstensen ( discusión ) 10:00 16 abr 2013 (UTC)
Felicitaciones por esto, capturando las 31 posibilidades (2^5-1). @Carstensen el código está más cerca de lo que crees. Ve al archivo svg y usa tu navegador para Ver | Fuente. La mayor parte son los marcadores de texto. La esencia son seis líneas: una <ellipse> y tres <use>. El centro de rotación parece estar desplazado un 17,5 % del radio mayor y un 22,5 % del radio menor. Código SVG muy inteligentemente elaborado. Bob Stein - VisiBone ( discusión ) 19:23 28 oct 2014 (UTC)
¡Dulce! ¡Gracias! Carstensen ( discusión ) 11:09, 10 de diciembre de 2014 (UTC)
ACTUALIZACIÓN 18 DE ABRIL DE 2016: ¡Apareció en The Guardian [4] en el 180 cumpleaños de John Venn !