Las mediciones de datación por radiocarbono producen edades en "años de radiocarbono", que deben convertirse en edades de calendario mediante un proceso llamado calibración . La calibración es necesaria porque la atmósfera14
C :12
La relación C , que es un elemento clave para calcular las edades del radiocarbono, no ha sido constante históricamente. [1]
Willard Libby , el inventor de la datación por radiocarbono, señaló ya en 1955 la posibilidad de que la relación pudiera haber variado con el tiempo. Empezaron a notarse discrepancias entre las edades medidas y las fechas históricas conocidas de los artefactos, y quedó claro que sería necesario aplicar una corrección a las edades de radiocarbono para obtener fechas de calendario. [2] Las fechas no calibradas pueden indicarse como "años de radiocarbono atrás", abreviado como "14
Adiós ". [3]
El término Before Present (BP) se estableció para informar las fechas derivadas del análisis de radiocarbono, donde "presente" es 1950. Las fechas no calibradas se indican como "uncal BP", [4] y las fechas calibradas (corregidas) como "cal BP". Utilizado solo, el término BP es ambiguo.
De manera similar, AC o AEC significa 'Antes de Cristo' o 'Antes de la era actual', y cal AC se utiliza en consecuencia.
Para producir una curva que pueda usarse para relacionar los años del calendario con los años de radiocarbono, se necesita una secuencia de muestras datadas de forma segura, que puedan analizarse para determinar su edad de radiocarbono. La dendrocronología , o el estudio de los anillos de los árboles, condujo a la primera secuencia de este tipo: los anillos de los árboles de piezas individuales de madera muestran secuencias características de anillos que varían en grosor debido a factores ambientales como la cantidad de lluvia en un año determinado. Esos factores afectan a todos los árboles de una zona, por lo que examinar las secuencias de anillos de los árboles de madera antigua permite la identificación de secuencias superpuestas. De esa manera, una secuencia ininterrumpida de anillos de los árboles puede extenderse mucho en el pasado. La primera secuencia publicada de este tipo, basada en los anillos de los árboles del pino longevo, fue creada en la década de 1960 por Wesley Ferguson . [7] Hans Suess utilizó los datos para publicar la primera curva de calibración para la datación por radiocarbono en 1967. [2] [8] [9] La curva mostró dos tipos de variación con respecto a la línea recta: una fluctuación a largo plazo con un período de aproximadamente 9.000 años y una variación a corto plazo, a menudo denominada "ondulaciones", con un período de décadas. Suess dijo que trazó la línea que muestra las ondulaciones mediante " schwung cósmico ", o a mano alzada. Durante algún tiempo no estuvo claro si las ondulaciones eran reales o no, pero ahora están bien establecidas. [8] [9]
El método de calibración también supone que la variación temporal en14
El nivel C es global, de modo que un pequeño número de muestras de un año específico son suficientes para la calibración, lo que se verificó experimentalmente en la década de 1980. [2]
Durante los siguientes 30 años, se publicaron muchas curvas de calibración utilizando una variedad de métodos y enfoques estadísticos. [10] Fueron reemplazadas por la serie de curvas INTCAL, comenzando con INTCAL98, publicada en 1998 y actualizada en 2004, 2009, 2013 y 2020. [11] Las mejoras de estas curvas se basan en nuevos datos recopilados de anillos de árboles, varvas , corales y otros estudios. Las adiciones significativas a los conjuntos de datos utilizados para INTCAL13 incluyen datos de foraminíferos marinos no varvados y espeleotemas datados por U-Th . Los datos de INTCAL13 incluyen curvas separadas para los hemisferios norte y sur, ya que difieren sistemáticamente debido al efecto del hemisferio; también hay una curva de calibración marina separada. [12] La curva de calibración para el hemisferio sur se conoce como SHCal en oposición a la IntCal para el hemisferio norte. La versión más reciente se publicó en 2020. También hay una curva diferente para el período posterior a 1955 debido a que las pruebas de bombas atómicas crearon niveles más altos de radiocarbono que varían según la latitud, conocidos como calibración de bomba.

Los métodos modernos de calibración toman la distribución normal original de los rangos de edad del radiocarbono y la utilizan para generar un histograma que muestra las probabilidades relativas de las edades del calendario. Esto se debe hacer mediante métodos numéricos en lugar de una fórmula porque la curva de calibración no se puede describir como una fórmula. [10] Los programas para realizar estos cálculos incluyen OxCal y CALIB. Se puede acceder a ellos en línea; permiten al usuario ingresar un rango de fechas con una desviación estándar de confianza para las edades del radiocarbono, seleccionar una curva de calibración y producir un resultado probabilístico tanto como datos tabulares como en forma gráfica. [13] [14]
En el ejemplo de salida de CALIB que se muestra a la izquierda, los datos de entrada son 1270 BP, con una desviación estándar de 10 años de radiocarbono. La curva seleccionada es la curva INTCAL13 del hemisferio norte, parte de la cual se muestra en la salida; el ancho vertical de la curva corresponde al ancho del error estándar en la curva de calibración en ese punto. Se muestra una distribución normal a la izquierda; estos son los datos de entrada, en años de radiocarbono. La parte central más oscura de la curva normal es el rango dentro de una desviación estándar de la media; el área gris más clara muestra el rango dentro de dos desviaciones estándar de la media. La salida está a lo largo del eje inferior; es un gráfico trimodal, con picos alrededor de 710 d. C., 740 d. C. y 760 d. C. Nuevamente, los rangos de confianza de 1σ están en gris oscuro y los rangos de confianza de 2σ están en gris claro. [14]
Antes de que la amplia disponibilidad de computadoras personales hiciera práctica la calibración probabilística, se utilizaba un método de "intercepción" más simple.
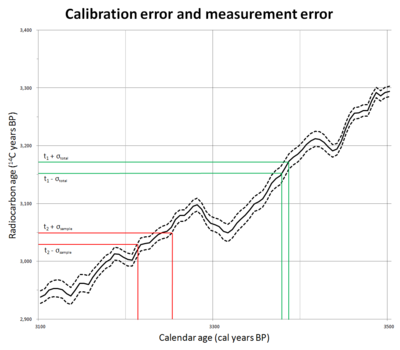
Una vez que las pruebas han producido una edad de muestra en años de radiocarbono con un rango de error asociado de más o menos una desviación estándar (generalmente escrito como ±σ), la curva de calibración se puede utilizar para derivar un rango de edades de calendario para la muestra. La curva de calibración en sí tiene un término de error asociado, que se puede ver en el gráfico denominado "Error de calibración y error de medición". Este gráfico muestra datos INTCAL13 para los años calendario 3100 a 3500 AP. La línea continua es la curva de calibración INTCAL13 y las líneas de puntos muestran el rango de error estándar, al igual que con el error de muestra, que es una desviación estándar. Simplemente leyendo el rango de años de radiocarbono contra las líneas de puntos, como se muestra para la muestra t 2 , en rojo, se obtiene un rango demasiado grande de años calendario. El término de error debe ser la raíz de la suma de los cuadrados de los dos errores: [15]
El ejemplo t 1 , en verde en el gráfico, muestra este procedimiento: el término de error resultante, σ total , se utiliza para el rango, y este rango se utiliza para leer el resultado directamente del gráfico mismo sin referencia a las líneas que muestran el error de calibración. [15]

Las variaciones en la curva de calibración pueden dar lugar a rangos de años calendario resultantes muy diferentes para muestras con diferentes edades de radiocarbono. El gráfico de la derecha muestra la parte de la curva de calibración INTCAL13 de 1000 BP a 1400 BP, un rango en el que hay desviaciones significativas de una relación lineal entre la edad de radiocarbono y la edad de calendario. En lugares donde la curva de calibración es pronunciada y no cambia de dirección, como en el ejemplo t 1 en azul en el gráfico de la derecha, el rango de años calendario resultante es bastante estrecho. Cuando la curva varía significativamente tanto hacia arriba como hacia abajo, un solo rango de fechas de radiocarbono puede producir dos o más rangos de años calendario separados. El ejemplo t 2 , en rojo en el gráfico, muestra esta situación: un rango de edad de radiocarbono de aproximadamente 1260 BP a 1280 BP se convierte en tres rangos separados entre aproximadamente 1190 BP y 1260 BP. Una tercera posibilidad es que la curva sea plana para algún rango de fechas de calendario; En este caso, ilustrado por t 3 , en verde en el gráfico, un rango de aproximadamente 30 años de radiocarbono, desde 1180 AP hasta 1210 AP, resulta en un rango de año calendario de aproximadamente un siglo, desde 1080 AP hasta 1180 AP. [10]
El método de intersección se basa únicamente en la posición de las intersecciones en el gráfico. Se considera que estas son los límites del rango de confianza del 68%, o una desviación estándar. Sin embargo, este método no hace uso del supuesto de que el rango de edad del radiocarbono original es una variable distribuida normalmente: no todas las fechas en el rango de edad del radiocarbono son igualmente probables, y por lo tanto no todas las fechas en la edad del año calendario resultante son igualmente probables. La derivación de un rango de años calendario por medio de intersecciones no tiene esto en cuenta. [10]
En el caso de un conjunto de muestras con una secuencia y una separación en el tiempo conocidas, como una secuencia de anillos de árboles, las edades de radiocarbono de las muestras forman un pequeño subconjunto de la curva de calibración. La curva resultante puede entonces coincidir con la curva de calibración real identificando dónde, en el rango sugerido por las fechas de radiocarbono, las ondulaciones en la curva de calibración coinciden mejor con las ondulaciones en la curva de fechas de la muestra. Esta técnica de "coincidencia de ondulaciones" puede conducir a una datación más precisa que la que es posible con las fechas de radiocarbono individuales. [16] Dado que los puntos de datos en la curva de calibración están separados por cinco años o más, y dado que se requieren al menos cinco puntos para una coincidencia, debe haber al menos un lapso de 25 años de datos de anillos de árboles (o similares) para que esta coincidencia sea posible. La coincidencia de ondulaciones se puede utilizar en lugares donde hay una meseta en la curva de calibración y, por lo tanto, puede proporcionar una fecha mucho más precisa que la que pueden producir los métodos de intersección o probabilidad. [17] La técnica no se limita a los anillos de los árboles; Por ejemplo, una secuencia de tefra estratificada en Nueva Zelanda, conocida por ser anterior a la colonización humana de las islas, ha sido datada en 1314 d. C. ± 12 años mediante el método de comparación de ondulación. [18]
Cuando se obtienen varias fechas de radiocarbono para muestras que se sabe o se sospecha que provienen del mismo objeto, puede ser posible combinar las mediciones para obtener una fecha más precisa. A menos que las muestras sean definitivamente de la misma edad (por ejemplo, si ambas fueron tomadas físicamente de un solo elemento), se debe aplicar una prueba estadística para determinar si las fechas se derivan del mismo objeto. Esto se hace calculando un término de error combinado para las fechas de radiocarbono para las muestras en cuestión y luego calculando una edad media agrupada. Luego es posible aplicar una prueba T para determinar si las muestras tienen la misma media verdadera. Una vez hecho esto, se puede calcular el error para la edad media agrupada, dando una respuesta final de una fecha y un rango únicos, con una distribución de probabilidad más estrecha (es decir, mayor precisión) como resultado de las mediciones combinadas. [19]
Las técnicas estadísticas bayesianas se pueden aplicar cuando hay varias fechas de radiocarbono que deben calibrarse. Por ejemplo, si se toma una serie de fechas de radiocarbono de diferentes niveles en una secuencia estratigráfica dada, el análisis bayesiano puede ayudar a determinar si algunas de las fechas deben descartarse como anomalías y puede utilizar la información para mejorar las distribuciones de probabilidad de salida. [16]
![]() Medios relacionados con Calibración de fechas de radiocarbono en Wikimedia Commons
Medios relacionados con Calibración de fechas de radiocarbono en Wikimedia Commons