
En teoría de grafos , un cografo , o gráfico reducible por complemento , o gráfico libre de P 4 , es un gráfico que puede generarse a partir del gráfico de un solo vértice K 1 mediante complementación y unión disjunta . Es decir, la familia de cografos es la clase más pequeña de grafos que incluye K 1 y está cerrada bajo complementación y unión disjunta.
Varios autores han descubierto las cografías de forma independiente desde la década de 1970; Las primeras referencias incluyen a Jung (1978), Lerchs (1971), Seinsche (1974) y Sumner (1974). También se les ha llamado gráficos D* , [1] gráficos hereditarios de Dacey (después del trabajo relacionado de James C. Dacey Jr. sobre redes ortomodulares ), [2] y gráficos de 2 paridades . [3] Tienen una descomposición estructural simple que involucra operaciones de unión disjunta y gráfico de complemento que pueden representarse de manera concisa mediante un árbol etiquetado y usarse algorítmicamente para resolver eficientemente muchos problemas, como encontrar la camarilla máxima , que son difíciles en clases de gráficos más generales.
Los casos especiales de los cografos incluyen los gráficos completos , los gráficos bipartitos completos , los gráficos de conglomerados y los gráficos de umbral . Las cografías son, a su vez, casos especiales de las gráficas hereditarias de distancia , las gráficas de permutación , las gráficas de comparabilidad y las gráficas perfectas .
Cualquier cografo se puede construir utilizando las siguientes reglas:
Los cografos se pueden definir como los gráficos que se pueden construir utilizando estas operaciones, a partir de los gráficos de un solo vértice. [4] Alternativamente, en lugar de usar la operación de complemento, se puede usar la operación de unión, que consiste en formar la unión disjunta y luego agregar una arista entre cada par de un vértice de y un vértice de .
Se pueden dar varias caracterizaciones alternativas de cografos. Entre ellos:
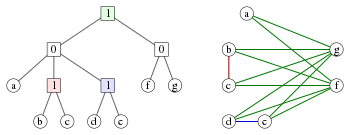
Un coárbol es un árbol en el que los nodos internos están etiquetados con los números 0 y 1. Cada coárbol T define un cografo G que tiene las hojas de T como vértices, y en el que el subárbol enraizado en cada nodo de T corresponde al subgrafo inducido. en G definido por el conjunto de hojas que descienden de ese nodo:
Una forma equivalente de describir el cografo formado a partir de un coárbol es que dos vértices están conectados por una arista si y sólo si el ancestro común más bajo de las hojas correspondientes está etiquetado con 1. A la inversa, cada cografo se puede representar de esta manera mediante un coárbol. . Si requerimos que las etiquetas en cualquier ruta de hoja raíz de este árbol alternen entre 0 y 1, esta representación es única. [4]
Los cografos pueden reconocerse en tiempo lineal y construirse una representación de coárbol mediante descomposición modular , [9] refinamiento de partición , [10] LexBFS , [11] o descomposición dividida . [12] Una vez que se ha construido una representación de coárbol, muchos problemas gráficos familiares se pueden resolver mediante simples cálculos ascendentes en los coárboles.
Por ejemplo, para encontrar la camarilla máxima en un cografo, calcule en orden de abajo hacia arriba la camarilla máxima en cada subgrafo representado por un subárbol del coárbol. Para un nodo etiquetado como 0, la camarilla máxima es la máxima entre las camarillas calculadas para los hijos de ese nodo. Para un nodo etiquetado como 1, la camarilla máxima es la unión de las camarillas calculadas para los hijos de ese nodo y tiene un tamaño igual a la suma de los tamaños de las camarillas de los hijos. Por lo tanto, maximizando y sumando alternativamente los valores almacenados en cada nodo del coárbol, podemos calcular el tamaño máximo de la camarilla, y maximizando y tomando uniones alternativamente, podemos construir la camarilla máxima misma. Cálculos de árbol ascendente similares permiten calcular el conjunto independiente máximo , el número de coloración de vértice , la cobertura de camarilla máxima y la hamiltonicidad (es decir, la existencia de un ciclo hamiltoniano ) en tiempo lineal a partir de una representación de coárbol de un cografo. [4] Debido a que los cografos tienen un ancho de camarilla acotado, el teorema de Courcelle puede usarse para probar cualquier propiedad en la lógica monádica de segundo orden de los grafos (MSO 1 ) en cografos en tiempo lineal. [13]
El problema de probar si un gráfico dado está a k vértices de distancia y/o t bordes de un cografo es manejable con parámetros fijos . [14] Decidir si un gráfico se puede eliminar k -borde a un cografo se puede resolver en O * (2.415 k ) tiempo, [15] y k -edge-editado a un cografo en O * (4.612 k ). [16] Si el subgrafo cografo inducido más grande de un gráfico se puede encontrar eliminando k vértices del gráfico, se puede encontrar en tiempo O * (3,30 k ). [15]
Dos cografos son isomorfos si y sólo si sus coárboles (en la forma canónica sin dos vértices adyacentes con la misma etiqueta) son isomorfos. Debido a esta equivalencia, se puede determinar en tiempo lineal si dos cografos son isomórficos, construyendo sus coárboles y aplicando una prueba de isomorfismo de tiempo lineal para árboles etiquetados. [4]
Si H es un subgrafo inducido de un cografo G , entonces H es en sí mismo un cografo; El coárbol de H se puede formar eliminando algunas de las hojas del coárbol de G y luego suprimiendo los nodos que tienen un solo hijo. Del teorema del árbol de Kruskal se deduce que la relación de ser un subgrafo inducido es un cuasi-ordenamiento en los cografos. [17] Por lo tanto, si una subfamilia de cografos (como los cografos planos ) se cierra bajo operaciones de subgrafos inducidos, entonces tiene un número finito de subgrafos inducidos prohibidos . Computacionalmente, esto significa que la prueba de pertenencia a dicha subfamilia se puede realizar en tiempo lineal, utilizando un cálculo ascendente en el coárbol de un gráfico determinado para probar si contiene alguno de estos subgrafos prohibidos. Sin embargo, cuando los tamaños de dos cografos son variables, probar si uno de ellos es un subgrafo inducido del otro es NP-completo . [18]
Los cografos juegan un papel clave en los algoritmos para reconocer funciones de lectura única . [19]
Algunos problemas de conteo también se vuelven manejables cuando la entrada se restringe a ser un cografo. Por ejemplo, existen algoritmos de tiempo polinomial para contar el número de camarillas o el número de camarillas máximas en un cografo. [4]
El número de cografos conectados con n vértices, para n = 1, 2, 3, ..., es:
Para n > 1 hay el mismo número de cografos desconectados, porque para cada cografo exactamente uno de él o su grafo complementario es conexo.
Todo gráfico completo K n es un cografo, con un coárbol que consta de un solo 1 nodo y n hojas. De manera similar, todo gráfico bipartito completo K a , b es un cografo. Su coárbol tiene sus raíces en un nodo 1 que tiene dos hijos de nodo 0, uno con hijos de hoja y otro con hijos de hoja b . Un grafo de Turán puede formarse mediante la unión de una familia de conjuntos independientes de igual tamaño; por lo tanto, también es un cografo, con un coárbol con raíz en un nodo 1 que tiene un nodo 0 secundario para cada conjunto independiente.
Cada gráfico de umbral es también un cografo. Se puede formar un gráfico de umbral agregando repetidamente un vértice, ya sea conectado a todos los vértices anteriores o a ninguno de ellos; cada una de estas operaciones es una de las operaciones de unión o unión disjuntas mediante las cuales se puede formar un coárbol. [20]
La caracterización de los cografos por la propiedad de que cada camarilla y conjunto independiente máximo tienen una intersección no vacía es una versión más fuerte de la propiedad definitoria de los grafos fuertemente perfectos , en los que cada subgrafo inducido contiene un conjunto independiente que intersecta a todos los camarillas máximas. En un cografo, cada conjunto máximo independiente intersecta a todos los camarillas máximas. Por tanto, todo cografo es fuertemente perfecto. [21]
El hecho de que los cografos estén libres de P4 implica que son perfectamente ordenables . De hecho, cada orden de vértice de un cografo es un orden perfecto, lo que implica además que la búsqueda de camarilla máxima y la coloración mínima se pueden encontrar en tiempo lineal con cualquier coloración voraz y sin la necesidad de una descomposición de coárbol.
Cada cografo es un gráfico hereditario de distancia , lo que significa que cada camino inducido en un cografo es el camino más corto . Los cografos se pueden caracterizar entre los gráficos hereditarios de distancia por tener un diámetro de como máximo dos en cada componente conectado. Cada cografo es también un gráfico de comparabilidad de un orden parcial en serie-paralelo , obtenido reemplazando las operaciones de unión y unión disjuntas mediante las cuales se construyó el cografo por operaciones de unión disjunta y suma ordinal en órdenes parciales. Debido a que los gráficos fuertemente perfectos, los gráficos perfectamente ordenables, los gráficos hereditarios de distancia y los gráficos de comparabilidad son todos gráficos perfectos , los cografos también son perfectos. [20]