En teoría de la información , un código de verificación de paridad de baja densidad ( LDPC ) es un código de corrección de errores lineal , un método para transmitir un mensaje a través de un canal de transmisión ruidoso . [1] [2] Un código LDPC se construye utilizando un gráfico de Tanner disperso (subclase del gráfico bipartito ). [3] Los códigos LDPC son códigos de aproximación a la capacidad , lo que significa que existen construcciones prácticas que permiten establecer el umbral de ruido muy cerca del máximo teórico (el límite de Shannon ) para un canal simétrico sin memoria. El umbral de ruido define un límite superior para el ruido del canal, hasta el cual la probabilidad de pérdida de información puede hacerse tan pequeña como se desee. Utilizando técnicas de propagación de creencias iterativas , los códigos LDPC se pueden decodificar en el tiempo de forma lineal en su longitud de bloque.
Los códigos LDPC también se conocen como códigos Gallager , en honor a Robert G. Gallager , quien desarrolló el concepto LDPC en su tesis doctoral en el Instituto Tecnológico de Massachusetts en 1960. [4] [5] Sin embargo, los códigos LDPC requieren una decodificación iterativa computacionalmente costosa, por lo que no se utilizaron durante décadas. En 1993, los códigos turbo recién inventados demostraron que los códigos con decodificación iterativa podían superar con creces a otros códigos utilizados en ese momento, pero los códigos turbo estaban patentados y requerían una tarifa para su uso. Esto generó un renovado interés en los códigos LDPC, que demostraron tener un rendimiento similar, pero eran mucho más antiguos y libres de patentes. [6] Ahora que la patente fundamental para los códigos turbo ha expirado (el 29 de agosto de 2013), [7] [8] los códigos LDPC todavía se utilizan por sus méritos técnicos.
Se ha demostrado que los códigos LDPC tienen propiedades combinatorias ideales. En su tesis, Gallager demostró que los códigos LDPC alcanzan el límite de Gilbert-Varshamov para códigos lineales sobre campos binarios con alta probabilidad. En 2020 se demostró que los códigos LDPC de Gallager logran la capacidad de decodificación de listas y también alcanzan el límite de Gilbert-Varshamov para códigos lineales sobre campos generales. [9]
Los códigos LDPC , que eran poco prácticos de implementar cuando Gallager los desarrolló por primera vez en 1963, [10] fueron olvidados hasta que su trabajo fue redescubierto en 1996. [11] Los códigos turbo , otra clase de códigos que se aproximaban a la capacidad descubiertos en 1993, se convirtieron en el esquema de codificación de elección a fines de la década de 1990, utilizados para aplicaciones como la Red de Espacio Profundo y las comunicaciones por satélite . Luego, los códigos LDPC recibieron un renovado interés como una alternativa libre de patentes de rendimiento similar. [6] Desde entonces, los avances en los códigos de verificación de paridad de baja densidad los han visto superar a los códigos turbo en términos de piso de error y rendimiento en el rango de tasa de código más alto , dejando a los códigos turbo más adecuados solo para las tasas de código más bajas. [12]
En 2003, un código LDPC de estilo de acumulación de repetición irregular (IRA) superó a seis códigos turbo y se convirtió en el código de corrección de errores en el nuevo estándar DVB-S2 para televisión digital . [13] El comité de selección de DVB-S2 realizó estimaciones de complejidad del decodificador para las propuestas de código turbo utilizando una arquitectura de decodificador en serie mucho menos eficiente en lugar de una arquitectura de decodificador en paralelo. Esto obligó a las propuestas de código turbo a utilizar tamaños de trama del orden de la mitad del tamaño de trama de las propuestas LDPC. [ cita requerida ]
En 2008, LDPC superó a los códigos turbo convolucionales como el sistema de corrección de errores hacia adelante (FEC) para el estándar ITU-T G.hn. [14] G.hn eligió los códigos LDPC en lugar de los códigos turbo debido a su menor complejidad de decodificación (especialmente cuando funcionan a velocidades de datos cercanas a 1,0 Gbit/s) y porque los códigos turbo propuestos exhibieron un piso de error significativo en el rango de operación deseado. [15]
Los códigos LDPC también se utilizan para Ethernet 10GBASE-T , que envía datos a 10 gigabits por segundo a través de cables de par trenzado. A partir de 2009, los códigos LDPC también forman parte del estándar Wi-Fi 802.11 como parte opcional de 802.11n y 802.11ac , en la especificación PHY de alto rendimiento (HT). [16] LDPC es una parte obligatoria de 802.11ax (Wi-Fi 6). [17]
Algunos sistemas OFDM agregan una corrección de error externa adicional que corrige los errores ocasionales (el "piso de error") que pasan el código interno de corrección LDPC incluso con tasas de error de bits bajas .
Por ejemplo: el código Reed-Solomon con modulación codificada LDPC (RS-LCM) utiliza un código externo Reed-Solomon. [18] Los estándares DVB-S2, DVB-T2 y DVB-C2 utilizan un código externo BCH para eliminar los errores residuales después de la decodificación LDPC. [19]
5G NR utiliza código polar para los canales de control y LDPC para los canales de datos. [20] [21]
Aunque el código LDPC ha tenido éxito en las unidades de disco duro comerciales, para explotar al máximo su capacidad de corrección de errores en las unidades SSD se requiere una detección de memoria flash de grano fino no convencional, lo que lleva a una mayor latencia de lectura de la memoria. LDPC en SSD [22] es un enfoque eficaz para implementar LDPC en SSD con un aumento de latencia muy pequeño, lo que convierte a LDPC en SSD en una realidad. Desde entonces, LDPC ha sido ampliamente adoptado en SSD comerciales tanto en los niveles de cliente como en los niveles empresariales por los principales proveedores de almacenamiento. Muchos SSD TLC (y posteriores) están utilizando códigos LDPC. Primero se intenta una decodificación dura rápida (borrado binario), que puede volver a la decodificación suave más lenta pero más poderosa. [23]
Los códigos LDPC se definen funcionalmente mediante una matriz de verificación de paridad dispersa . Esta matriz dispersa suele generarse aleatoriamente, sujeta a las restricciones de dispersión (la construcción de códigos LDPC se analiza más adelante). Estos códigos fueron diseñados por primera vez por Robert Gallager en 1960. [5]
A continuación se muestra un fragmento de gráfico de un código LDPC de ejemplo que utiliza la notación de gráfico factorial de Forney . En este gráfico, n nodos variables en la parte superior del gráfico están conectados a ( n − k ) nodos de restricción en la parte inferior del gráfico.
Esta es una forma popular de representar gráficamente un código LDPC ( n , k ). Los bits de un mensaje válido, cuando se colocan en las T en la parte superior del gráfico, satisfacen las restricciones gráficas. Específicamente, todas las líneas que se conectan a un nodo variable (casilla con un signo "=") tienen el mismo valor, y todos los valores que se conectan a un nodo factor (casilla con un signo "+") deben sumar, módulo dos, cero (en otras palabras, deben sumar un número par; o debe haber un número par de valores impares).
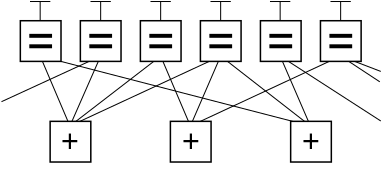
Ignorando las líneas que salen de la imagen, hay ocho posibles cadenas de seis bits correspondientes a palabras de código válidas: (es decir, 000000, 011001, 110010, 101011, 111100, 100101, 001110, 010111). Este fragmento de código LDPC representa un mensaje de tres bits codificado como seis bits. Aquí se utiliza redundancia para aumentar la posibilidad de recuperación de errores de canal. Este es un código lineal (6, 3) , con n = 6 y k = 3.
Nuevamente ignorando las líneas que salen de la imagen, la matriz de verificación de paridad que representa este fragmento de gráfico es
En esta matriz, cada fila representa una de las tres restricciones de verificación de paridad, mientras que cada columna representa uno de los seis bits de la palabra de código recibida.
En este ejemplo, las ocho palabras de código se pueden obtener colocando la matriz de verificación de paridad H en esta forma a través de operaciones de fila básicas en GF(2) :
Paso 1: H.
Paso 2: La fila 1 se agrega a la fila 3.
Paso 3: Se intercambian las filas 2 y 3.
Paso 4: La fila 1 se agrega a la fila 3.
A partir de esto, la matriz generadora G se puede obtener como (observando que en el caso especial de que se trate de un código binario ), o específicamente:
Finalmente, al multiplicar las ocho cadenas de 3 bits posibles por G , se obtienen las ocho palabras de código válidas. Por ejemplo, la palabra de código para la cadena de bits '101' se obtiene de la siguiente manera:
¿Dónde está el símbolo de la multiplicación módulo 2?
A modo de comprobación, el espacio de filas de G es ortogonal a H tal que
La cadena de bits '101' se encuentra como los primeros 3 bits de la palabra de código '101011'.

Durante la codificación de una trama, los bits de datos de entrada (D) se repiten y se distribuyen a un conjunto de codificadores constituyentes. Los codificadores constituyentes suelen ser acumuladores y cada acumulador se utiliza para generar un símbolo de paridad. Se transmite una única copia de los datos originales (S 0,K-1 ) con los bits de paridad (P) para formar los símbolos de código. Los bits S de cada codificador constituyente se descartan.
El bit de paridad puede utilizarse dentro de otro código constituyente.
En un ejemplo en el que se utiliza el código DVB-S2 de tasa 2/3, el tamaño del bloque codificado es de 64800 símbolos (N=64800) con 43200 bits de datos (K=43200) y 21600 bits de paridad (M=21600). Cada código constituyente (nodo de comprobación) codifica 16 bits de datos, excepto el primer bit de paridad, que codifica 8 bits de datos. Los primeros 4680 bits de datos se repiten 13 veces (se utilizan en 13 códigos de paridad), mientras que los bits de datos restantes se utilizan en 3 códigos de paridad (código LDPC irregular).
A modo de comparación, los códigos turbo clásicos suelen utilizar dos códigos constituyentes configurados en paralelo, cada uno de los cuales codifica todo el bloque de entrada (K) de bits de datos. Estos codificadores constituyentes son códigos convolucionales recursivos (RSC) de profundidad moderada (8 o 16 estados) que están separados por un entrelazador de códigos que entrelaza una copia de la trama.
El código LDPC, por el contrario, utiliza muchos códigos constituyentes de baja profundidad (acumuladores) en paralelo, cada uno de los cuales codifica solo una pequeña parte del marco de entrada. Los numerosos códigos constituyentes pueden considerarse como muchos " códigos convolucionales " de baja profundidad (2 estados) que están conectados mediante las operaciones de repetición y distribución. Las operaciones de repetición y distribución realizan la función del entrelazador en el código turbo.
La capacidad de gestionar con mayor precisión las conexiones de los diversos códigos constituyentes y el nivel de redundancia para cada bit de entrada otorgan más flexibilidad en el diseño de códigos LDPC, lo que puede generar un mejor rendimiento que los códigos turbo en algunos casos. Los códigos turbo todavía parecen tener un mejor rendimiento que los LDPC a tasas de código bajas, o al menos el diseño de códigos de tasa baja con buen rendimiento es más fácil para los códigos turbo.
En la práctica, el hardware que forma los acumuladores se reutiliza durante el proceso de codificación. Es decir, una vez que se genera un primer conjunto de bits de paridad y se almacenan los bits de paridad, se utiliza el mismo hardware acumulador para generar un siguiente conjunto de bits de paridad.
Al igual que con otros códigos, la decodificación de máxima verosimilitud de un código LDPC en el canal simétrico binario es un problema NP-completo , [24] demostrado por la reducción a partir de la correspondencia tridimensional . Por lo tanto, suponiendo que P != NP , lo cual es una creencia generalizada, realizar una decodificación óptima para un código arbitrario de cualquier tamaño útil no es práctico.
Sin embargo, las técnicas subóptimas basadas en la decodificación iterativa de propagación de creencias dan resultados excelentes y se pueden implementar en la práctica. Las técnicas de decodificación subóptimas consideran cada comprobación de paridad que compone el LDPC como un código de comprobación de paridad única (SPC) independiente. Cada código SPC se decodifica por separado utilizando técnicas de entrada suave y salida suave (SISO) como SOVA , BCJR , MAP y otros derivados de las mismas. La información de decisión suave de cada decodificación SISO se verifica y actualiza con otras decodificaciones SPC redundantes del mismo bit de información. A continuación, cada código SPC se decodifica de nuevo utilizando la información de decisión suave actualizada. Este proceso se repite hasta que se obtiene una palabra de código válida o se agota la decodificación. Este tipo de decodificación se conoce a menudo como decodificación de suma-producto.
La decodificación de los códigos SPC a menudo se denomina procesamiento de "nodo de verificación", y la verificación cruzada de las variables a menudo se denomina procesamiento de "nodo de variable".
En una implementación práctica de un decodificador LDPC, los conjuntos de códigos SPC se decodifican en paralelo para aumentar el rendimiento.
Por el contrario, la propagación de creencias en el canal de borrado binario es particularmente simple cuando consiste en la satisfacción iterativa de restricciones.
Por ejemplo, considere que la palabra de código válida, 101011, del ejemplo anterior, se transmite a través de un canal de borrado binario y se recibe con el primer y cuarto bit borrados para obtener ?01?11. Dado que el mensaje transmitido debe haber satisfecho las restricciones del código, el mensaje se puede representar escribiendo el mensaje recibido en la parte superior del gráfico de factores.
En este ejemplo, el primer bit no se puede recuperar todavía, porque todas las restricciones conectadas a él tienen más de un bit desconocido. Para continuar con la decodificación del mensaje, se deben identificar las restricciones que se conectan a solo uno de los bits borrados. En este ejemplo, solo la segunda restricción es suficiente. Al examinar la segunda restricción, el cuarto bit debe haber sido cero, ya que solo un cero en esa posición satisfaría la restricción.
Luego se repite este procedimiento. El nuevo valor del cuarto bit se puede utilizar ahora junto con la primera restricción para recuperar el primer bit, como se ve a continuación. Esto significa que el primer bit debe ser un uno para satisfacer la restricción más a la izquierda.

De esta manera, el mensaje puede decodificarse iterativamente. En otros modelos de canal, los mensajes que pasan entre los nodos variables y los nodos de verificación son números reales , que expresan probabilidades y posibilidades de creencia.
Este resultado se puede validar multiplicando la palabra de código corregida r por la matriz de comprobación de paridad H :
Dado que el resultado z (el síndrome ) de esta operación es el vector cero tres × uno, la palabra de código resultante r se valida exitosamente.
Una vez completada la decodificación, los bits del mensaje original '101' se pueden extraer observando los primeros 3 bits de la palabra clave.
Si bien es ilustrativo, este ejemplo de borrado no muestra el uso de decodificación de decisión suave o de paso de mensajes de decisión suave, que se utiliza en prácticamente todos los decodificadores LDPC comerciales.
En los últimos años [ ¿cuándo? ] , también se ha dedicado una gran cantidad de trabajo al estudio de los efectos de programaciones alternativas para la actualización de nodos variables y nodos de restricción. La técnica original que se utilizó para decodificar códigos LDPC se conocía como inundación . Este tipo de actualización requería que, antes de actualizar un nodo variable, todos los nodos de restricción debían actualizarse y viceversa. En un trabajo posterior de Vila Casado et al. [ 25] , se estudiaron técnicas de actualización alternativas, en las que los nodos variables se actualizan con la información más reciente disponible sobre los nodos de verificación. [ cita requerida ]
La intuición detrás de estos algoritmos es que los nodos variables cuyos valores varían más son los que necesitan ser actualizados primero. Los nodos altamente confiables, cuya magnitud de razón de verosimilitud logarítmica (LLR) es grande y no cambia significativamente de una actualización a la siguiente, no requieren actualizaciones con la misma frecuencia que otros nodos, cuyo signo y magnitud fluctúan más ampliamente. [ cita requerida ] Estos algoritmos de programación muestran una mayor velocidad de convergencia y niveles de error más bajos que aquellos que utilizan inundación. Estos niveles de error más bajos se logran mediante la capacidad del algoritmo Informed Dynamic Scheduling (IDS) [25] para superar los conjuntos de trampas de palabras de código cercanas. [26]
Cuando se utilizan algoritmos de programación sin inundación, se utiliza una definición alternativa de iteración. Para un código LDPC ( n , k ) de tasa k / n , se produce una iteración completa cuando se han actualizado n variables y n − k nodos de restricción, sin importar el orden en que se actualizaron. [ cita requerida ]
Para tamaños de bloque grandes, los códigos LDPC se construyen comúnmente estudiando primero el comportamiento de los decodificadores. Como el tamaño de bloque tiende a infinito, se puede demostrar que los decodificadores LDPC tienen un umbral de ruido por debajo del cual la decodificación se logra de manera confiable, y por encima del cual no se logra, [27] conocido coloquialmente como el efecto acantilado . Este umbral se puede optimizar encontrando la mejor proporción de arcos de nodos de verificación y arcos de nodos variables. Un enfoque gráfico aproximado para visualizar este umbral es un gráfico EXIT . [ cita requerida ]
La construcción de un código LDPC específico después de esta optimización se divide en dos tipos principales de técnicas: [ cita requerida ]
La construcción mediante un enfoque pseudoaleatorio se basa en resultados teóricos que indican que, para bloques de gran tamaño, una construcción aleatoria ofrece un buen rendimiento de decodificación. [11] En general, los códigos pseudoaleatorios tienen codificadores complejos, pero los códigos pseudoaleatorios con los mejores decodificadores pueden tener codificadores simples. [28] A menudo se aplican varias restricciones para ayudar a garantizar que las propiedades deseadas esperadas en el límite teórico de tamaño de bloque infinito se produzcan en un tamaño de bloque finito. [ cita requerida ]
Se pueden utilizar enfoques combinatorios para optimizar las propiedades de códigos LDPC de tamaño de bloque pequeño o para crear códigos con codificadores simples. [ cita requerida ]
Algunos códigos LDPC se basan en códigos Reed–Solomon , como el código RS-LDPC utilizado en el estándar Ethernet de 10 Gigabits . [29] En comparación con los códigos LDPC generados aleatoriamente, los códigos LDPC estructurados (como el código LDPC utilizado en el estándar DVB-S2 ) pueden tener un hardware más simple y, por lo tanto, de menor costo; en particular, los códigos construidos de manera que la matriz H sea una matriz circulante . [30]
Otra forma de construir códigos LDPC es utilizar geometrías finitas . Este método fue propuesto por Y. Kou et al. en 2001. [31]
Los códigos LDPC se pueden comparar con otros esquemas de codificación potentes, por ejemplo, los códigos turbo . [32] Por un lado, el rendimiento BER de los códigos turbo está influenciado por las limitaciones de los códigos bajos. [33] Los códigos LDPC no tienen limitaciones de distancia mínima, [34] lo que indirectamente significa que los códigos LDPC pueden ser más eficientes en tasas de código relativamente grandes (por ejemplo, 3/4, 5/6, 7/8) que los códigos turbo. Sin embargo, los códigos LDPC no son el reemplazo completo: los códigos turbo son la mejor solución en las tasas de código más bajas (por ejemplo, 1/6, 1/3, 1/2). [35] [36]
Hasta el momento sólo hay una capacidad para lograr código mediante diseño y prueba.