stringtranslate.com

Círculo ortocentroidal

Un triángulo (negro), su ortocentro (azul), su centroide (rojo) y su disco ortocentroidal (amarillo)
  Círculo ortocentroidal delimitado por el ortocentro (H) y el baricentro (S)
  Línea de Euler , en la que se encuentran el circuncentro (O) y el centro de nueve puntos (N) junto con H y S
  F 1 y F 2 : Puntos de Fermat
  F: Punto de Feuerbach
  Yo: Incentro
  G: Punto Gergonne
  U: Punto simmediano

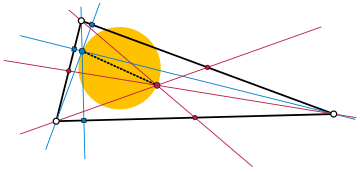
En geometría , el círculo ortocentroidal de un triángulo no equilátero es el círculo que tiene el ortocentro y el baricentro del triángulo en extremos opuestos de su diámetro . Este diámetro también contiene el centro de nueve puntos del triángulo y es un subconjunto de la línea de Euler , que también contiene el circuncentro fuera del círculo ortocentroidal.

Andrew Guinand demostró en 1984 que el incentro del triángulo debe estar en el interior del círculo ortocentroidal, pero sin coincidir con el centro de nueve puntos; es decir, debe caer en el disco ortocentroidal abierto perforado en el centro de nueve puntos. [1] [2] [3] [4] [5] : pp. 451–452  El incentro podría ser cualquiera de esos puntos, dependiendo del triángulo específico que tenga ese disco ortocentroidal particular. [3]

Además, [2] el punto de Fermat , el punto de Gergonne y el punto simediano están en el disco ortocentroidal abierto perforado en su propio centro (y podrían estar en cualquier punto del mismo), mientras que el segundo punto de Fermat y el punto de Feuerbach están en el exterior del círculo ortocentroidal. El conjunto de ubicaciones potenciales de uno u otro de los puntos de Brocard es también el disco ortocentroidal abierto. [6]

El cuadrado del diámetro del círculo ortocentroidal es [7] : p.102  donde a, b y c son las longitudes de los lados del triángulo y D es el diámetro de su círculo circunscrito .

Referencias

  1. ^ Guinand, Andrew P. (1984), "Líneas de Euler, centros tritangentes y sus triángulos", American Mathematical Monthly , 91 (5): 290–300, doi :10.2307/2322671, JSTOR  2322671.
  2. ^ ab Bradley, Christopher J.; Smith, Geoff C. (2006), "Las ubicaciones de los centros de los triángulos", Forum Geometricorum , 6 : 57–70.
  3. ^ ab Stern, Joseph (2007), "El problema de determinación del triángulo de Euler" (PDF) , Forum Geometricorum , 7 : 1–9.
  4. ^ Franzsen, William N. (2011), "La distancia desde el incentro a la línea de Euler", Forum Geometricorum , 11 : 231–236.
  5. ^ Leversha, Gerry; Smith, GC (noviembre de 2007), "Euler y la geometría de triángulos", Mathematical Gazette , 91 (522): 436–452, doi :10.1017/S0025557200182087, JSTOR  40378417, S2CID  125341434.
  6. ^ Bradley, Christopher J.; Smith, Geoff C. (2006), "Las ubicaciones de los puntos de Brocard", Forum Geometricorum , 6 : 71–77.
  7. ^ Altshiller-Court, Nathan, Geometría universitaria , Dover Publications, 2007 (orig. Barnes & Noble 1952).

Enlaces externos