En lógica proposicional , una fórmula proposicional es un tipo de fórmula sintáctica que está bien formada . Si se dan los valores de todas las variables en una fórmula proposicional, se determina un valor de verdad único . Una fórmula proposicional también puede denominarse expresión proposicional , oración o fórmula oracional .
Una fórmula proposicional se construye a partir de proposiciones simples , como "cinco es mayor que tres" o variables proposicionales como p y q , utilizando conectivos u operadores lógicos como NOT, AND, OR o IMPLIES; por ejemplo:
En matemáticas , una fórmula proposicional suele denominarse de forma más breve " proposición ", pero, más precisamente, una fórmula proposicional no es una proposición sino una expresión formal que denota una proposición , un objeto formal en discusión, al igual que una expresión como " x + y " no es un valor, sino que denota un valor. En algunos contextos, mantener la distinción puede ser importante.
Para los propósitos del cálculo proposicional, las proposiciones (enunciados, oraciones, aserciones) se consideran simples o compuestas. [1] Las proposiciones compuestas se consideran unidas por conectores oracionales, algunos de los más comunes de los cuales son "Y", "O", "SI ... ENTONCES ...", "NI ... NI ...", "... ES EQUIVALENTE A ..." . El punto y coma de enlace ";", y el conector "PERO" se consideran expresiones de "Y". Una secuencia de oraciones discretas se considera unida por "Y", y el análisis formal aplica una "regla de paréntesis" recursiva con respecto a las secuencias de proposiciones simples (ver más abajo sobre fórmulas bien formadas).
Las proposiciones simples son de naturaleza declarativa, es decir, hacen afirmaciones sobre la condición o naturaleza de un objeto particular de sensación, por ejemplo, "Esta vaca es azul", "¡Hay un coyote!" ("Ese coyote ESTÁ allí , detrás de las rocas"). [2] Por lo tanto, las afirmaciones "primitivas" simples deben ser sobre objetos específicos o estados mentales específicos. Cada una debe tener al menos un sujeto (un objeto inmediato de pensamiento u observación), un verbo (en voz activa y tiempo presente preferiblemente) y quizás un adjetivo o adverbio. "¡Perro!" probablemente implica "Veo un perro", pero debe rechazarse por ser demasiado ambiguo.
Para los propósitos del cálculo proposicional, una proposición compuesta generalmente puede reformularse en una serie de oraciones simples, aunque el resultado probablemente suene forzado.
El cálculo de predicados va un paso más allá que el cálculo proposicional y se trata de un "análisis de la estructura interna de las proposiciones" [3]. Descompone una oración simple en dos partes (i) su sujeto (el objeto ( singular o plural) del discurso) y (ii) un predicado (un verbo o posiblemente una cláusula verbal que afirma una cualidad o atributo del objeto u objetos). El cálculo de predicados luego generaliza la forma "sujeto|predicado" (donde | simboliza la concatenación (unión) de símbolos) en una forma con la siguiente estructura de sujeto en blanco "___|predicado", y el predicado a su vez se generaliza a todas las cosas con esa propiedad.
La generalización de "este cerdo" a un miembro (potencial) de dos clases "cosas aladas" y "cosas azules" significa que tiene una relación de verdad con ambas clases. En otras palabras, dado un dominio de discurso "cosas aladas", se encuentra que p es un miembro de este dominio o no. Por lo tanto, existe una relación W (alado) entre p (cerdo) y { T, F }, W(p) se evalúa como { T, F } donde { T, F } es el conjunto de los valores booleanos "verdadero" y "falso". Lo mismo ocurre con B (azul) y p (cerdo) y { T, F }: B(p) se evalúa como { T, F }. Por lo tanto, ahora se pueden analizar las afirmaciones conectadas "B(p) AND W(p)" para su valor de verdad general, es decir:
En particular, las oraciones simples que emplean nociones de "todos", "algunos", "unos pocos", "uno de", etc., llamadas cuantificadores lógicos, son tratadas por el cálculo de predicados. Junto con el nuevo simbolismo de función "F(x)", se introducen dos nuevos símbolos: ∀ (Para todos) y ∃ (Existe..., existe al menos uno de..., etc.). El cálculo de predicados, pero no el cálculo proposicional, puede establecer la validez formal de la siguiente afirmación:
Tarski afirma que la noción de IDENTIDAD (a diferencia de la EQUIVALENCIA LÓGICA) se encuentra fuera del cálculo proposicional; sin embargo, señala que para que una lógica sea útil para las matemáticas y las ciencias debe contener una "teoría" de IDENTIDAD. [4] Algunos autores hacen referencia a la "lógica de predicados con identidad" para enfatizar esta extensión. Ver más sobre esto a continuación.
Un álgebra (y hay muchas diferentes), definida de forma vaga, es un método mediante el cual se manipulan una colección de símbolos llamados variables junto con otros símbolos como los paréntesis (, ) y algún subconjunto de símbolos como *, +, ~, &, ∨, =, ≡, ∧, ¬ dentro de un sistema de reglas. Se dice que estos símbolos, y cadenas bien formadas de ellos, representan objetos, pero en un sistema algebraico específico estos objetos no tienen significados. Por lo tanto, el trabajo dentro del álgebra se convierte en un ejercicio de obediencia a ciertas leyes (reglas) de la sintaxis del álgebra (formación de símbolos) en lugar de en la semántica (significado) de los símbolos. Los significados se encuentran fuera del álgebra.
Para que una secuencia bien formada de símbolos en el álgebra —una fórmula— tenga alguna utilidad fuera del álgebra, a los símbolos se les asignan significados y eventualmente a las variables se les asignan valores; luego, mediante una serie de reglas, se evalúa la fórmula.
Cuando los valores se restringen a sólo dos y se aplican a la noción de oraciones simples (por ejemplo, enunciados hablados o aserciones escritas) vinculadas por conectores proposicionales, todo este sistema algebraico de símbolos, reglas y métodos de evaluación se denomina habitualmente cálculo proposicional o cálculo oracional.
Si bien algunas de las reglas conocidas del álgebra aritmética siguen siendo válidas en el álgebra de proposiciones (por ejemplo, las leyes conmutativas y asociativas para AND y OR), otras no (por ejemplo, las leyes distributivas para AND, OR y NOT).
Análisis: En el razonamiento deductivo , los filósofos, retóricos y matemáticos reducen los argumentos a fórmulas y luego los estudian (normalmente con tablas de verdad ) para comprobar su corrección (solidez). Por ejemplo: ¿Es sólido el siguiente argumento?
Los ingenieros analizan los circuitos lógicos que han diseñado utilizando técnicas de síntesis y luego aplican diversas técnicas de reducción y minimización para simplificar sus diseños.
Síntesis: Los ingenieros, en particular, sintetizan fórmulas proposicionales (que finalmente terminan siendo circuitos de símbolos) a partir de tablas de verdad . Por ejemplo, se podría escribir una tabla de verdad que muestre cómo debería comportarse la suma binaria dada la suma de las variables "b" y "a" y "carry_in" "ci", y los resultados "carry_out" "co" y "sum" Σ:
El tipo más simple de fórmula proposicional es una variable proposicional . Las proposiciones que son expresiones simbólicas simples ( atómicas ) a menudo se denotan por variables llamadas p , q , o P , Q , etc. Una variable proposicional tiene como objetivo representar una proposición atómica (afirmación), como "Es sábado" = p (aquí el símbolo = significa "... se le asigna la variable llamada ...") o "Sólo voy al cine los lunes" = q .
La evaluación de una fórmula proposicional comienza con la asignación de un valor de verdad a cada variable. Como cada variable representa una oración simple, los valores de verdad se aplican a la "verdad" o "falsedad" de estas oraciones simples.
Valores de verdad en la retórica, la filosofía y las matemáticas
Los valores de verdad son sólo dos: {VERDAD "T", FALSEDAD "F"}. Un empirista pone todas las proposiciones en dos grandes clases: analíticas —verdaderas sin importar lo que sean (por ejemplo, tautología ), y sintéticas —derivadas de la experiencia y por lo tanto susceptibles de confirmación por terceros (la teoría de verificación del significado). [5] Los empiristas sostienen que, en general, para llegar al valor de verdad de una proposición sintética , los significados (plantillas de comparación de patrones) primero deben aplicarse a las palabras, y luego estas plantillas de significado deben compararse con lo que sea que se esté afirmando. Por ejemplo, mi enunciado "¡Esa vaca es azul !" ¿Es esta afirmación una VERDAD? Verdaderamente lo dije. Y tal vez estoy viendo una vaca azul —a menos que esté mintiendo, mi afirmación es una VERDAD relativa al objeto de mi (quizás defectuosa) percepción—. Pero ¿la vaca azul está "realmente allí"? ¿Qué ves cuando miras por la misma ventana? Para proceder a una verificación, necesitará una noción previa (una plantilla) tanto de "vaca" como de " azul ", y una capacidad de hacer coincidir las plantillas con el objeto de la sensación (si es que existe uno). [ cita requerida ]
Valores de verdad en la ingeniería
Los ingenieros intentan evitar las nociones de verdad y falsedad que atormentan a los filósofos, pero en el análisis final los ingenieros deben confiar en sus instrumentos de medición. En su búsqueda de robustez , los ingenieros prefieren extraer objetos conocidos de una pequeña biblioteca: objetos que tienen comportamientos predecibles y bien definidos incluso en grandes combinaciones (de ahí su nombre para el cálculo proposicional: "lógica combinatoria"). Los comportamientos más pequeños de un solo objeto son dos (por ejemplo, { OFF, ON }, { open, shut }, { UP, DOWN } etc.), y estos se ponen en correspondencia con { 0, 1 }. Tales elementos se denominan digitales ; aquellos con un rango continuo de comportamientos se denominan analógicos . Siempre que se deben tomar decisiones en un sistema analógico, muy a menudo un ingeniero convertirá un comportamiento analógico (la puerta está 45.32146% ARRIBA) a digital (por ejemplo, ABAJO=0 ) mediante el uso de un comparador . [6]
Por lo tanto, la asignación de significado de las variables y los dos símbolos de valor { 0, 1 } proviene "de fuera" de la fórmula que representa el comportamiento del objeto (normalmente) compuesto. Un ejemplo es una puerta de garaje con dos "interruptores de límite", uno para ARRIBA etiquetado como SW_U y otro para ABAJO etiquetado como SW_D, y cualquier otra cosa que haya en el circuito de la puerta. La inspección del circuito (ya sea el diagrama o los objetos reales en sí mismos: puerta, interruptores, cables, placa de circuito, etc.) podría revelar que, en la placa de circuito, el "nodo 22" va a +0 voltios cuando los contactos del interruptor "SW_D" están mecánicamente en contacto ("cerrados") y la puerta está en la posición "abajo" (95% abajo), y el "nodo 29" va a +0 voltios cuando la puerta está 95% ARRIBA y los contactos del interruptor SW_U están en contacto mecánico ("cerrados"). [7] El ingeniero debe definir los significados de estos voltajes y todas las combinaciones posibles (las 4), incluidas las "malas" (por ejemplo, ambos nodos 22 y 29 a 0 voltios, lo que significa que la puerta está abierta y cerrada al mismo tiempo). El circuito responde sin pensar a cualquier voltaje que experimente sin ninguna conciencia de VERDAD o FALSEDAD, CORRECTO o INCORRECTO, SEGURO o PELIGROSO. [ cita requerida ]
Las fórmulas proposicionales arbitrarias se construyen a partir de variables proposicionales y otras fórmulas proposicionales utilizando conectores proposicionales . Algunos ejemplos de conectores incluyen:
Los siguientes son los conectores comunes a la retórica, la filosofía y las matemáticas junto con sus tablas de verdad . Los símbolos utilizados variarán de un autor a otro y entre los campos de estudio. En general, las abreviaturas "T" y "F" representan las evaluaciones VERDAD y FALSEDAD aplicadas a las variables en la fórmula proposicional (por ejemplo, la afirmación: "Esa vaca es azul" tendrá el valor de verdad "T" para Verdad o "F" para Falsedad, según sea el caso).
Los conectores se utilizan de distintas formas, por ejemplo, "a IMPLICA b" también se dice "SI a ENTONCES b". Algunas de ellas se muestran en la tabla.
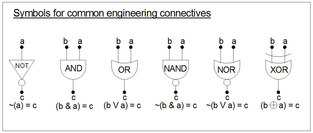
En general, los conectores de ingeniería son exactamente iguales a los conectores de matemáticas, excepto que tienden a evaluarse con "1" = "T" y "0" = "F". Esto se hace con fines de análisis/minimización y síntesis de fórmulas mediante el uso de la noción de minterms y mapas de Karnaugh (ver más abajo). Los ingenieros también usan las palabras producto lógico de la noción de Boole (a*a = a) y suma lógica de la noción de Jevons (a+a = a). [8]
El conectivo IF... THEN... ELSE... aparece como la forma más simple del operador CASE de la teoría de la recursión y la teoría de la computación y es el conectivo responsable de los goto condicionales (saltos, ramificaciones). A partir de este conectivo se pueden construir todos los demás conectivos (ver más abajo). Aunque "IF c THEN b ELSE a" suena como una implicación, es, en su forma más reducida, un interruptor que toma una decisión y ofrece como resultado solo una de dos alternativas "a" o "b" (de ahí el nombre de sentencia switch en el lenguaje de programación C ). [9]
Las siguientes tres proposiciones son equivalentes (como lo indica el signo de equivalencia lógica ≡ ):
Por lo tanto, SI... ENTONCES... EN OTRO LUGAR—a diferencia de la implicación—no se evalúa como una "VERDAD" ambigua cuando la primera proposición es falsa, es decir, c = F en (c → b). Por ejemplo, la mayoría de las personas rechazarían la siguiente proposición compuesta como un non sequitur sin sentido porque la segunda oración no está conectada en significado con la primera. [10]
En reconocimiento de este problema, el signo → de implicación formal en el cálculo proposicional se denomina implicación material para distinguirla de la implicación intuitiva cotidiana. [a]
El uso de la construcción IF ... THEN ... ELSE evita la controversia porque ofrece una elección completamente determinista entre dos alternativas establecidas; ofrece dos "objetos" (las dos alternativas b y a), y selecciona entre ellos de manera exhaustiva e inequívoca. [12] En la tabla de verdad a continuación, d1 es la fórmula: ( (IF c THEN b) AND (IF NOT-c THEN a) ). Su forma completamente reducida d2 es la fórmula: ( (c AND b) OR (NOT-c AND a). Las dos fórmulas son equivalentes como lo muestran las columnas "=d1" y "=d2". Los ingenieros eléctricos llaman a la fórmula completamente reducida el operador AND-OR-SELECT. El operador CASE (o SWITCH) es una extensión de la misma idea a n resultados posibles, pero mutuamente excluyentes. Los ingenieros eléctricos llaman al operador CASE un multiplexor .
La primera tabla de esta sección comienza con la entrada equivalencia lógica para señalar el hecho de que " equivalencia lógica " no es lo mismo que "identidad". Por ejemplo, la mayoría estaría de acuerdo en que la afirmación "Esa vaca es azul" es idéntica a la afirmación "Esa vaca es azul". Por otro lado, la equivalencia lógica a veces aparece en el habla como en este ejemplo: "'El sol está brillando' significa 'estoy en bicicleta'". Traducido a una fórmula proposicional las palabras se convierten en: "SI 'el sol está brillando' ENTONCES 'estoy en bicicleta', Y SI 'estoy en bicicleta' ENTONCES 'el sol está brillando'": [13]
Distintos autores utilizan distintos signos para la equivalencia lógica: ↔ (p. ej., Suppes, Goodstein, Hamilton), ≡ (p. ej., Robbin), ⇔ (p. ej., Bender y Williamson). Normalmente, la identidad se escribe como el signo igual =. Una excepción a esta regla se encuentra en Principia Mathematica . Para más información sobre la filosofía de la noción de IDENTIDAD, véase la ley de Leibniz .
Como se señaló anteriormente, Tarski considera que la IDENTIDAD está fuera del cálculo proposicional, pero afirma que sin la noción, la "lógica" es insuficiente para las matemáticas y las ciencias deductivas. De hecho, el signo entra en el cálculo proposicional cuando se debe evaluar una fórmula. [14]
En algunos sistemas no hay tablas de verdad, sino sólo axiomas formales (por ejemplo, cadenas de símbolos de un conjunto { ~, →, (, ), variables p 1 , p 2 , p 3 , ... } y reglas de formación de fórmulas (reglas sobre cómo hacer más cadenas de símbolos a partir de cadenas anteriores mediante el uso de, por ejemplo, sustitución y modus ponens ). El resultado de dicho cálculo será otra fórmula (es decir, una cadena de símbolos bien formada). Eventualmente, sin embargo, si uno quiere usar el cálculo para estudiar nociones de validez y verdad, uno debe agregar axiomas que definan el comportamiento de los símbolos llamados "los valores de verdad" {V, F} (o {1, 0}, etc.) en relación con los otros símbolos.
Por ejemplo, Hamilton utiliza dos símbolos = y ≠ cuando define la noción de una valoración v de cualesquiera fórmulas bien formadas (fbf) A y B en su "cálculo de enunciados formales" L. Una valoración v es una función de las fbf de su sistema L hasta el rango (salida) { T, F }, dado que a cada variable p 1 , p 2 , p 3 en una fbf se le asigna un valor de verdad arbitrario { T, F }.
Las dos definiciones ( i ) y ( ii ) definen el equivalente de las tablas de verdad para los conectores ~ (NO) y → (IMPLICACIÓN) de su sistema. La primera deriva F ≠ T y T ≠ F, en otras palabras, " v ( A ) no significa v (~ A )". La definición ( ii ) especifica la tercera fila de la tabla de verdad, y las otras tres filas provienen entonces de una aplicación de la definición ( i ). En particular, ( ii ) asigna el valor F (o un significado de "F") a la expresión completa. Las definiciones también sirven como reglas de formación que permiten la sustitución de un valor previamente derivado en una fórmula:
Algunos sistemas formales especifican estos axiomas de valoración desde el principio en forma de ciertas fórmulas, como la ley de contradicción o las leyes de identidad y nulidad. La elección de cuáles utilizar, junto con leyes como la de conmutación y distribución, depende del diseñador del sistema, siempre que el conjunto de axiomas sea completo (es decir, suficiente para formar y evaluar cualquier fórmula bien formada creada en el sistema).
Como se muestra arriba, el conectivo CASE (IF c THEN b ELSE a ) se construye a partir de los conectivos de 2 argumentos IF ... THEN ... y AND o de OR y AND y el NOT de 1 argumento. Los conectivos como el AND de n argumentos (a & b & c & ... & n), OR (a ∨ b ∨ c ∨ ... ∨ n) se construyen a partir de cadenas de AND y OR de dos argumentos y se escriben en forma abreviada sin los paréntesis. Estos, y otros conectivos también, se pueden usar como bloques de construcción para aún más conectivos. Los retóricos, filósofos y matemáticos usan tablas de verdad y los diversos teoremas para analizar y simplificar sus fórmulas.
La ingeniería eléctrica utiliza símbolos dibujados y los conecta con líneas que representan el acto matemático de sustitución y reemplazo. Luego verifican sus dibujos con tablas de verdad y simplifican las expresiones como se muestra a continuación mediante el uso de mapas de Karnaugh o teoremas. De esta manera, los ingenieros han creado una gran cantidad de "lógica combinatoria" (es decir, conectores sin retroalimentación) como "decodificadores", "codificadores", "puertas multifunción", "lógica mayoritaria", "sumadores binarios", "unidades lógicas aritméticas", etc.
Una definición crea un nuevo símbolo y su comportamiento, a menudo con fines de abreviación. Una vez que se presenta la definición, se puede utilizar cualquier forma del símbolo o fórmula equivalente. El siguiente simbolismo = Df sigue la convención de Reichenbach. [15] Algunos ejemplos de definiciones convenientes extraídas del conjunto de símbolos { ~, &, (, ) } y variables. Cada definición produce una fórmula lógicamente equivalente que se puede utilizar para sustitución o reemplazo.
Las definiciones anteriores para OR, IMPLICACIÓN, XOR y equivalencia lógica son en realidad esquemas (o "esquemas"), es decir, son modelos (demostraciones, ejemplos) para un formato de fórmula general pero mostrados (con fines ilustrativos) con letras específicas a, b, c para las variables, mientras que cualquier letra de variable puede ir en sus lugares siempre que las sustituciones de letras sigan la regla de sustitución a continuación.
Sustitución : La variable o subfórmula que se va a sustituir por otra variable, constante o subfórmula debe reemplazarse en todos los casos en toda la fórmula general.
Reemplazo : (i) la fórmula a reemplazar debe estar dentro de una tautología, es decir, ser lógicamente equivalente (conectada por ≡ o ↔) a la fórmula que la reemplaza, y (ii) a diferencia de la sustitución, es permisible que el reemplazo ocurra solo en un lugar (es decir, para una fórmula).
La presentación clásica de la lógica proposicional (véase Enderton 2002) utiliza los conectores . El conjunto de fórmulas sobre un conjunto dado de variables proposicionales se define inductivamente como el conjunto más pequeño de expresiones tales que:
Esta definición inductiva puede ampliarse fácilmente para cubrir conectivos adicionales.
La definición inductiva también puede reformularse en términos de una operación de cierre (Enderton 2002). Sea V un conjunto de variables proposicionales y sea X V el conjunto de todas las cadenas de un alfabeto que incluye símbolos en V , paréntesis izquierdo y derecho, y todos los conectores lógicos en consideración. Cada conector lógico corresponde a una operación de construcción de fórmulas, una función de XX V a XX V :
El conjunto de fórmulas sobre V se define como el subconjunto más pequeño de XX V que contiene a V y está cerrado bajo todas las operaciones de construcción de fórmulas.
Las siguientes "leyes" del cálculo proposicional se utilizan para "reducir" fórmulas complejas. Las "leyes" se pueden verificar fácilmente con tablas de verdad. Para cada ley, el conectivo principal (el más externo) está asociado con la equivalencia lógica ≡ o identidad =. Un análisis completo de las 2 n combinaciones de valores de verdad para sus n variables distintas dará como resultado una columna de 1 (T) debajo de este conectivo. Este hallazgo hace que cada ley, por definición, sea una tautología. Y, para una ley dada, debido a que sus fórmulas a la izquierda y a la derecha son equivalentes (o idénticas), pueden sustituirse entre sí.
Los lectores emprendedores podrían desafiarse a sí mismos a inventar un "sistema axiomático" que utilice los símbolos { ∨, &, ~, (, ), las variables a, b, c }, las reglas de formación especificadas anteriormente y la menor cantidad posible de las leyes enumeradas a continuación, y luego derivar como teoremas los demás, así como las valoraciones de la tabla de verdad para ∨, & y ~. Un conjunto atribuido a Huntington (1904) (Suppes:204) utiliza ocho de las leyes definidas a continuación.
Si se utilizan en un sistema axiomático, los símbolos 1 y 0 (o V y F) se consideran fórmulas bien formadas y, por lo tanto, obedecen a las mismas reglas que las variables. Por lo tanto, las leyes enumeradas a continuación son en realidad esquemas axiomáticos , es decir, sustituyen a un número infinito de instancias. Por lo tanto, ( x ∨ y ) ≡ ( y ∨ x ) podría usarse en una instancia, ( p ∨ 0 ) ≡ ( 0 ∨ p ) y en otra instancia ( 1 ∨ q ) ≡ ( q ∨ 1 ), etc.
En general, para evitar confusiones durante el análisis y la evaluación de fórmulas proposicionales, se puede hacer un uso liberal de los paréntesis. Sin embargo, con mucha frecuencia los autores los omiten. Para analizar una fórmula complicada, primero hay que saber la antigüedad o rango que tiene cada uno de los conectivos (excepto *) sobre los otros conectivos. Para "formar bien" una fórmula, hay que empezar con el conectivo de mayor rango y añadir paréntesis alrededor de sus componentes, para luego ir descendiendo en el rango (prestando mucha atención al alcance del conectivo sobre el que está trabajando). Desde el más antiguo hasta el menos antiguo, con los signos de predicado ∀x y ∃x, la IDENTIDAD = y los signos aritméticos añadidos para completar: [b]
Por lo tanto, la fórmula se puede analizar, pero como NOT no obedece la ley distributiva, los paréntesis alrededor de la fórmula interna (~c y ~d) son obligatorios:
Tanto AND como OR obedecen la ley conmutativa y la ley asociativa :
Omisión de paréntesis en cadenas de AND y OR : los conectivos se consideran unarios (de una variable, p. ej. NOT) y binarios (es decir, AND, OR, IMPLIES de dos variables). Por ejemplo:
Sin embargo, una demostración de tabla de verdad muestra que la forma sin los paréntesis adicionales es perfectamente adecuada.
Omisión de paréntesis en el caso de un NOT de una sola variable : si bien ~(a) donde a es una sola variable es perfectamente claro, ~a es adecuado y es la forma habitual en que aparecería este literal . Cuando el NOT se encuentra sobre una fórmula con más de un símbolo, entonces los paréntesis son obligatorios, por ejemplo, ~(a ∨ b).
OR se distribuye sobre AND y AND se distribuye sobre OR. NOT no se distribuye sobre AND u OR. Vea a continuación la ley de De Morgan:
NOT, cuando se distribuye sobre OR o AND, hace algo peculiar (de nuevo, esto se puede verificar con una tabla de verdad):
La absorción, en particular la primera, hace que las "leyes" de la lógica difieran de las "leyes" de la aritmética:
El signo "=" (a diferencia de la equivalencia lógica ≡, alternativamente ↔ o ⇔) simboliza la asignación de valor o significado. Por lo tanto, la cadena (a & ~(a)) simboliza "0", es decir, significa lo mismo que el símbolo "0". En algunos "sistemas", esto será un axioma (definición) que tal vez se muestre como ( (a & ~(a)) = Df 0 ); en otros sistemas, puede derivarse de la tabla de verdad siguiente:
Una propiedad clave de las fórmulas es que se pueden analizar de forma única para determinar la estructura de la fórmula en términos de sus variables proposicionales y conectores lógicos. Cuando las fórmulas se escriben en notación infija , como se indicó anteriormente, se garantiza la legibilidad única mediante un uso apropiado de paréntesis en la definición de fórmulas. Alternativamente, las fórmulas se pueden escribir en notación polaca o notación polaca inversa , eliminando por completo la necesidad de paréntesis.
La definición inductiva de fórmulas infijas de la sección anterior se puede convertir a una gramática formal en forma Backus-Naur :
< fórmula > ::= < variable proposicional >
| ( ¬ < fórmula > )| ( < fórmula > ∧ < fórmula > )| ( < fórmula > ∨ < fórmula > )| ( < fórmula > → < fórmula > )| ( < fórmula > ↔ < fórmula > )Se puede demostrar que cualquier expresión que coincida con la gramática tiene un número equilibrado de paréntesis izquierdos y derechos, y cualquier segmento inicial no vacío de una fórmula tiene más paréntesis izquierdos que derechos. [17] Este hecho se puede utilizar para proporcionar un algoritmo para analizar fórmulas. Por ejemplo, supongamos que una expresión x comienza con . Comenzando después del segundo símbolo, coincida con la subexpresión más corta y de x que tenga paréntesis equilibrados. Si x es una fórmula, queda exactamente un símbolo después de esta expresión, este símbolo es un paréntesis de cierre e y en sí mismo es una fórmula. Esta idea se puede utilizar para generar un analizador descendente recursivo para fórmulas.
Ejemplo de conteo entre paréntesis :
Este método ubica como "1" el conectivo principal —el conectivo bajo el cual ocurre la evaluación general de la fórmula para los paréntesis más externos (que a menudo se omiten). [18] También ubica el conectivo más interno donde uno comenzaría la evaluación de la fórmula sin el uso de una tabla de verdad, por ejemplo en el "nivel 6".
La noción de argumento válido se aplica habitualmente a las inferencias en argumentos, pero los argumentos se reducen a fórmulas proposicionales y pueden evaluarse de la misma manera que cualquier otra fórmula proposicional. Aquí, una inferencia válida significa: "La fórmula que representa la inferencia se evalúa como "verdad" bajo su conectivo principal, sin importar qué valores de verdad se asignen a sus variables", es decir, la fórmula es una tautología. [19] Es muy posible que una fórmula esté bien formada pero no sea válida. Otra forma de decir esto es: "Estar bien formada es necesario para que una fórmula sea válida, pero no es suficiente ". La única forma de averiguar si está bien formada y es válida es someterla a verificación con una tabla de verdad o mediante el uso de las "leyes":

Un conjunto de conectivos lógicos se denomina completo si cada fórmula proposicional es tautológicamente equivalente a una fórmula con solo los conectivos en ese conjunto. Hay muchos conjuntos completos de conectivos, incluidos , , y . Hay dos conectivos binarios que son completos por sí mismos, correspondientes a NAND y NOR, respectivamente. [20] Algunos pares no son completos, por ejemplo .
El conector binario correspondiente a NAND se denomina trazo de Sheffer y se escribe con una barra vertical | o una flecha vertical ↑. La completitud de este conector se observó en Principia Mathematica (1927:xvii). Dado que es completo por sí solo, todos los demás conectores se pueden expresar utilizando solo el trazo. Por ejemplo, donde el símbolo " ≡ " representa la equivalencia lógica :
En particular, los conectivos cero-arios (que representan la verdad) y (que representan la falsedad) se pueden expresar utilizando el trazo:
Este conectivo junto con { 0, 1 }, ( o { F, T } o { , } ) forma un conjunto completo. En lo que sigue, la relación IF...THEN...ELSE (c, b, a) = d representa ( (c → b) ∨ (~c → a) ) ≡ ( (c & b) ∨ (~c & a) ) = d
Ejemplo: A continuación se muestra cómo se llevaría a cabo una prueba basada en un teorema de "(c, b, 1) ≡ (c → b)". A continuación se muestra la verificación de la tabla de verdad. (Nota: (c → b) se define como (~c ∨ b)):
En la siguiente tabla de verdad, la columna etiquetada como "tensa" para la tautología evalúa la equivalencia lógica (simbolizada aquí por ≡) entre las dos columnas etiquetadas como d. Debido a que las cuatro filas bajo "tensa" son 1, la equivalencia representa de hecho una tautología.
Una fórmula proposicional arbitraria puede tener una estructura muy complicada. A menudo resulta conveniente trabajar con fórmulas que tienen formas más simples, conocidas como formas normales . Algunas formas normales comunes incluyen la forma normal conjuntiva y la forma normal disyuntiva . Cualquier fórmula proposicional se puede reducir a su forma normal conjuntiva o disyuntiva.

La reducción a la forma normal es relativamente sencilla una vez que se prepara una tabla de verdad para la fórmula. Pero los intentos posteriores de minimizar el número de literales (ver más abajo) requieren algunas herramientas: la reducción mediante las leyes de De Morgan y las tablas de verdad puede ser difícil de manejar, pero los mapas de Karnaugh son muy adecuados para un número pequeño de variables (5 o menos). Existen algunos métodos tabulares sofisticados para circuitos más complejos con múltiples salidas, pero estos están más allá del alcance de este artículo; para más información, consulte el algoritmo de Quine-McCluskey .
En ingeniería eléctrica, una variable x o su negación ~(x) se puede denominar literal . Una cadena de literales conectados por AND se denomina término. Una cadena de literales conectados por OR se denomina alterm. Normalmente, el literal ~(x) se abrevia ~x. A veces, el símbolo & se omite por completo a modo de multiplicación algebraica.
De la misma manera que una tabla de verdad de 2 n filas muestra la evaluación de una fórmula proposicional para todos los 2 n valores posibles de sus variables, n variables produce un mapa de Karnaugh de 2 n cuadrados (aunque no podemos dibujarlo en su realización de dimensión completa). Por ejemplo, 3 variables producen 2 3 = 8 filas y 8 cuadrados de Karnaugh; 4 variables producen 16 filas de tabla de verdad y 16 cuadrados y, por lo tanto, 16 mintérminos . Cada cuadrado del mapa de Karnaugh y su evaluación de tabla de verdad correspondiente representa un mintérmino.
Cualquier fórmula proposicional puede reducirse a la "suma lógica" (OR) de los mintérminos activos (es decir, de valor "1" o "T"). Cuando está en esta forma, se dice que la fórmula está en forma normal disyuntiva . Pero, aunque esté en esta forma, no está necesariamente minimizada con respecto al número de términos ni al número de literales.
En la siguiente tabla, observe la peculiar numeración de las filas: (0, 1, 3, 2, 6, 7, 5, 4, 0). La primera columna es el equivalente decimal del equivalente binario de los dígitos "cba", es decir:
Esta numeración se debe a que, a medida que uno se desplaza por la tabla de fila en fila, solo una variable a la vez cambia su valor. El código Gray se deriva de esta noción. Esta noción se puede extender a hipercubos tridimensionales y cuatridimensionales llamados diagramas de Hasse, en los que las variables de cada esquina cambian solo una a la vez a medida que uno se desplaza por los bordes del cubo. Los diagramas de Hasse (hipercubos) aplanados en dos dimensiones son diagramas de Veitch o mapas de Karnaugh (que son prácticamente lo mismo).
Al trabajar con mapas de Karnaugh, siempre hay que tener en cuenta que el borde superior "envuelve" al borde inferior, y el borde izquierdo envuelve al borde derecho: el diagrama de Karnaugh es en realidad un objeto aplanado tridimensional, cuatridimensional o ndimensional.
Veitch mejoró la noción de diagramas de Venn al convertir los círculos en cuadrados contiguos, y Karnaugh simplificó el diagrama de Veitch al convertir los mintérminos, escritos en su forma literal (por ejemplo, ~abc~d) en números. [21] El método procede de la siguiente manera:
Genere la tabla de verdad de la fórmula. Numere sus filas utilizando los equivalentes binarios de las variables (normalmente, secuencialmente, de 0 a n-1) para n variables.
Ejemplo: ((c & d) ∨ (p & ~(c & (~d)))) = q en forma normal conjuntiva es:
Sin embargo, esta fórmula se puede reducir tanto en el número de términos (de 4 a 3) como en el recuento total de sus literales (de 12 a 6).

Utilice los valores de la fórmula (por ejemplo, "p") obtenidos mediante el método de la tabla de verdad y colóquelos en sus respectivos cuadrados de Karnaugh (asociados) (estos se numeran según la convención del código Gray). Si aparecen valores de "d" para "no importa" en la tabla, esto agrega flexibilidad durante la fase de reducción.
Los minitérminos de cuadrados 1 adyacentes (contiguos) (cuadrados T) se pueden reducir con respecto al número de sus literales , y los términos numéricos también se reducirán en el proceso. Dos cuadrados contiguos (2 x 1 horizontal o 1 x 2 vertical, incluso los bordes representan cuadrados contiguos) pierden un literal, cuatro cuadrados en un rectángulo de 4 x 1 (horizontal o vertical) o un cuadrado de 2 x 2 (incluso las cuatro esquinas representan cuadrados contiguos) pierden dos literales, ocho cuadrados en un rectángulo pierden 3 literales, etc. (Se busca el cuadrado o rectángulos más grandes e ignora los cuadrados o rectángulos más pequeños contenidos totalmente dentro de él). Este proceso continúa hasta que se tienen en cuenta todos los cuadrados contiguos, momento en el que se minimiza la fórmula proposicional.
Por ejemplo, los cuadrados n.° 3 y n.° 7 son adyacentes. Estos dos cuadrados adyacentes pueden perder un literal (por ejemplo, "p" de los cuadrados n.° 3 y n.° 7), cuatro cuadrados en un rectángulo o cuadrado pierden dos literales, ocho cuadrados en un rectángulo pierden 3 literales, etc. (Se busca el cuadrado o los rectángulos más grandes). Este proceso continúa hasta que se tienen en cuenta todos los cuadrados adyacentes, momento en el que se dice que la fórmula proposicional se minimiza.
Ejemplo: El método del mapa se realiza generalmente por inspección. El siguiente ejemplo amplía el método algebraico para mostrar el "truco" detrás de la combinación de términos en un mapa de Karnaugh:
Observe que, por la ley de idempotencia (A ∨ A) = A, podemos crear más términos. Luego, por las leyes de asociación y distribución, las variables que desaparecen se pueden emparejar y luego "desaparecer" con la ley de contradicción (x & ~x) = 0. A continuación, se utilizan corchetes [ y ] solo para hacer un seguimiento de los términos; no tienen un significado especial:
Dados los siguientes ejemplos-como-definiciones, ¿qué se puede pensar del razonamiento subsiguiente?
Then assign the variable "s" to the left-most sentence "This sentence is simple". Define "compound" c = "not simple" ~s, and assign c = ~s to "This sentence is compound"; assign "j" to "It [this sentence] is conjoined by AND". The second sentence can be expressed as:
If truth values are to be placed on the sentences c = ~s and j, then all are clearly FALSEHOODS: e.g. "This sentence is complex" is a FALSEHOOD (it is simple, by definition). So their conjunction (AND) is a falsehood. But when taken in its assembled form, the sentence a TRUTH.
This is an example of the paradoxes that result from an impredicative definition—that is, when an object m has a property P, but the object m is defined in terms of property P.[22] The best advice for a rhetorician or one involved in deductive analysis is avoid impredicative definitions but at the same time be on the lookout for them because they can indeed create paradoxes. Engineers, on the other hand, put them to work in the form of propositional formulas with feedback.
The notion of a propositional formula appearing as one of its own variables requires a formation rule that allows the assignment of the formula to a variable. In general there is no stipulation (either axiomatic or truth-table systems of objects and relations) that forbids this from happening.[23]
The simplest case occurs when an OR formula becomes one its own inputs e.g. p = q. Begin with (p ∨ s) = q, then let p = q. Observe that q's "definition" depends on itself "q" as well as on "s" and the OR connective; this definition of q is thus impredicative. Either of two conditions can result:[24] oscillation or memory.
It helps to think of the formula as a black box. Without knowledge of what is going on "inside" the formula-"box" from the outside it would appear that the output is no longer a function of the inputs alone. That is, sometimes one looks at q and sees 0 and other times 1. To avoid this problem one has to know the state (condition) of the "hidden" variable p inside the box (i.e. the value of q fed back and assigned to p). When this is known the apparent inconsistency goes away.
To understand [predict] the behavior of formulas with feedback requires the more sophisticated analysis of sequential circuits. Propositional formulas with feedback lead, in their simplest form, to state machines; they also lead to memories in the form of Turing tapes and counter-machine counters. From combinations of these elements one can build any sort of bounded computational model (e.g. Turing machines, counter machines, register machines, Macintosh computers, etc.).
In the abstract (ideal) case the simplest oscillating formula is a NOT fed back to itself: ~(~(p=q)) = q. Analysis of an abstract (ideal) propositional formula in a truth-table reveals an inconsistency for both p=1 and p=0 cases: When p=1, q=0, this cannot be because p=q; ditto for when p=0 and q=1.

Oscillation with delay: If a delay[25] (ideal or non-ideal) is inserted in the abstract formula between p and q then p will oscillate between 1 and 0: 101010...101... ad infinitum. If either of the delay and NOT are not abstract (i.e. not ideal), the type of analysis to be used will be dependent upon the exact nature of the objects that make up the oscillator; such things fall outside mathematics and into engineering.
Analysis requires a delay to be inserted and then the loop cut between the delay and the input "p". The delay must be viewed as a kind of proposition that has "qd" (q-delayed) as output for "q" as input. This new proposition adds another column to the truth table. The inconsistency is now between "qd" and "p" as shown in red; two stable states resulting:

Without delay, inconsistencies must be eliminated from a truth table analysis. With the notion of "delay", this condition presents itself as a momentary inconsistency between the fed-back output variable q and p = qdelayed.
A truth table reveals the rows where inconsistencies occur between p = qdelayed at the input and q at the output. After "breaking" the feed-back,[26] the truth table construction proceeds in the conventional manner. But afterwards, in every row the output q is compared to the now-independent input p and any inconsistencies between p and q are noted (i.e. p=0 together with q=1, or p=1 and q=0); when the "line" is "remade" both are rendered impossible by the Law of contradiction ~(p & ~p)). Rows revealing inconsistencies are either considered transient states or just eliminated as inconsistent and hence "impossible".
About the simplest memory results when the output of an OR feeds back to one of its inputs, in this case output "q" feeds back into "p". Given that the formula is first evaluated (initialized) with p=0 & q=0, it will "flip" once when "set" by s=1. Thereafter, output "q" will sustain "q" in the "flipped" condition (state q=1). This behavior, now time-dependent, is shown by the state diagram to the right of the once-flip.
The next simplest case is the "set-reset" flip-flop shown below the once-flip. Given that r=0 & s=0 and q=0 at the outset, it is "set" (s=1) in a manner similar to the once-flip. It however has a provision to "reset" q=0 when "r"=1. And additional complication occurs if both set=1 and reset=1. In this formula, the set=1 forces the output q=1 so when and if (s=0 & r=1) the flip-flop will be reset. Or, if (s=1 & r=0) the flip-flop will be set. In the abstract (ideal) instance in which s=1 ⇒ s=0 & r=1 ⇒ r=0 simultaneously, the formula q will be indeterminate (undecidable). Due to delays in "real" OR, AND and NOT the result will be unknown at the outset but thereafter predicable.
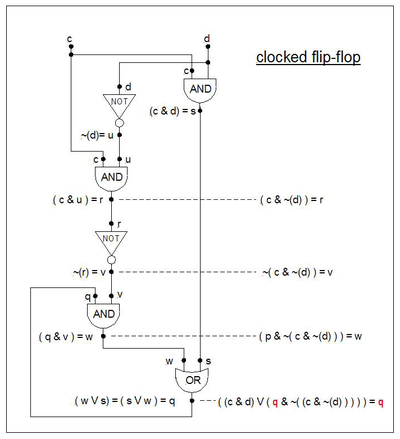
The formula known as "clocked flip-flop" memory ("c" is the "clock" and "d" is the "data") is given below. It works as follows: When c = 0 the data d (either 0 or 1) cannot "get through" to affect output q. When c = 1 the data d "gets through" and output q "follows" d's value. When c goes from 1 to 0 the last value of the data remains "trapped" at output "q". As long as c=0, d can change value without causing q to change.
The state diagram is similar in shape to the flip-flop's state diagram, but with different labelling on the transitions.
Bertrand Russell (1912:74) lists three laws of thought that derive from Aristotle: (1) The law of identity: "Whatever is, is.", (2) The law of noncontradiction: "Nothing can both be and not be", and (3) The law of excluded middle: "Everything must be or not be."
The use of the word "everything" in the law of excluded middle renders Russell's expression of this law open to debate. If restricted to an expression about BEING or QUALITY with reference to a finite collection of objects (a finite "universe of discourse") -- the members of which can be investigated one after another for the presence or absence of the assertion—then the law is considered intuitionistically appropriate. Thus an assertion such as: "This object must either BE or NOT BE (in the collection)", or "This object must either have this QUALITY or NOT have this QUALITY (relative to the objects in the collection)" is acceptable. See more at Venn diagram.
Although a propositional calculus originated with Aristotle, the notion of an algebra applied to propositions had to wait until the early 19th century. In an (adverse) reaction to the 2000 year tradition of Aristotle's syllogisms, John Locke's Essay concerning human understanding (1690) used the word semiotics (theory of the use of symbols). By 1826 Richard Whately had critically analyzed the syllogistic logic with a sympathy toward Locke's semiotics. George Bentham's work (1827) resulted in the notion of "quantification of the predicate" (1827) (nowadays symbolized as ∀ ≡ "for all"). A "row" instigated by William Hamilton over a priority dispute with Augustus De Morgan "inspired George Boole to write up his ideas on logic, and to publish them as MAL [Mathematical Analysis of Logic] in 1847" (Grattin-Guinness and Bornet 1997:xxviii).
About his contribution Grattin-Guinness and Bornet comment:
Gottlob Frege's massive undertaking (1879) resulted in a formal calculus of propositions, but his symbolism is so daunting that it had little influence excepting on one person: Bertrand Russell. First as the student of Alfred North Whitehead he studied Frege's work and suggested a (famous and notorious) emendation with respect to it (1904) around the problem of an antinomy that he discovered in Frege's treatment ( cf Russell's paradox ). Russell's work led to a collaboration with Whitehead that, in the year 1912, produced the first volume of Principia Mathematica (PM). It is here that what we consider "modern" propositional logic first appeared. In particular, PM introduces NOT and OR and the assertion symbol ⊦ as primitives. In terms of these notions they define IMPLICATION → ( def. *1.01: ~p ∨ q ), then AND (def. *3.01: ~(~p ∨ ~q) ), then EQUIVALENCE p ←→ q (*4.01: (p → q) & ( q → p ) ).
Computation and switching logic: