Rompecabezas de equilibrio

Rompecabezas de lógica

Un acertijo de equilibrio o de pesaje es un acertijo de lógica que consiste en equilibrar objetos (a menudo monedas) para determinar cuál tiene un valor diferente, utilizando una balanza un número limitado de veces. Estos acertijos se diferencian de los que asignan pesos a los objetos en que solo es relevante la masa relativa de estos.

Por ejemplo, al detectar una moneda diferente en tres pesajes (n = 3), el número máximo de monedas que se pueden analizar es ⁠3 ³ − 1/2⁠ = 13. Nótese que con 3 pesos y 13 monedas, no siempre es posible determinar la identidad de la última moneda (si es más pesada o más liviana que el resto), sino simplemente que la moneda es diferente. En general, con n pesos, puedes determinar la identidad de una moneda si tienes ⁠3 ⁿ − 1/2- 1 o menos monedas. En el caso de n = 3, puedes descubrir realmente la identidad de la moneda diferente entre 12 monedas.

Esta versión de doce monedas del problema apareció impresa ya en 1945 ^{[2] [3]} y Guy y Nowakowski explican que "fue popular en ambos lados del Atlántico durante la Segunda Guerra Mundial; incluso se sugirió que se lanzara sobre Alemania en un intento de sabotear su esfuerzo bélico". ^[3]

Problema de las nueve monedas

Solución al problema de la balanza para 9 monedas en 2 pesajes, donde la moneda impar es más liviana que las demás: si la moneda impar fuera más pesada que las demás, se intercambian las dos ramas superiores en cada decisión de pesaje

Un ejemplo bien conocido es el de hasta nueve objetos, por ejemplo monedas (o bolas), que tienen el mismo peso, excepto uno, que es más ligero que los demás: una falsificación (una bola extraña). La diferencia es perceptible solo al pesarlas en una balanza , pero solo se pueden pesar las monedas en sí. ¿Cómo se puede aislar la moneda falsa con solo dos pesadas?

Solución

Para encontrar una solución, primero consideramos el número máximo de objetos entre los cuales se puede encontrar el más liviano en una sola pesada. El número máximo posible es tres. Para encontrar el más liviano, podemos comparar dos monedas cualesquiera, dejando fuera la tercera. Si las dos monedas pesan lo mismo, entonces la moneda más liviana debe ser una de las que no están en la balanza. De lo contrario, es la que la balanza indica como más liviana.

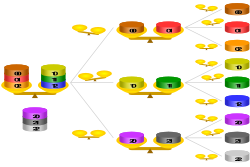
Ahora, imaginemos las nueve monedas en tres pilas de tres monedas cada una. En un movimiento podemos encontrar cuál de las tres pilas es más ligera (es decir, la que contiene la moneda más ligera). Luego, solo hace falta un movimiento más para identificar la moneda más ligera dentro de esa pila más ligera. Por lo tanto, en dos pesajes, podemos encontrar una sola moneda ligera de un conjunto de 3 × 3 = 9 .

Por extensión, se necesitarían sólo tres pesajes para encontrar la moneda ligera impar entre 27 monedas, y cuatro pesajes para encontrarla entre 81 monedas.

Problema de las doce monedas

Una versión más compleja tiene doce monedas, once de las cuales son idénticas. Si una es diferente, no sabemos si es más pesada o más liviana que las otras. Esta vez, la balanza puede usarse tres veces para determinar si hay una moneda única y, si la hay, para aislarla y determinar su peso en relación con las demás. (Este acertijo y su solución aparecieron por primera vez en un artículo en 1945. ^[4] ) El problema tiene una variante más simple con tres monedas en dos pesadas y una variante más compleja con 39 monedas en cuatro pesadas.

Solución

Este problema tiene más de una solución. Una de ellas es fácilmente escalable a un número mayor de monedas utilizando numeración de base tres: etiquetando cada moneda con un número diferente de tres dígitos en base tres y colocando en el n -ésimo peso todas las monedas que estén etiquetadas con el n -ésimo dígito idéntico a la etiqueta de la placa (con tres placas, una a cada lado de la balanza etiquetadas con 0 y 2, y una fuera de la balanza etiquetada con 1). Otros procedimientos paso a paso son similares al siguiente. Es menos sencillo para este problema, y ​​el segundo y tercer pesaje dependen de lo que haya sucedido anteriormente, aunque ese no tiene por qué ser el caso (ver más abajo).

• Se colocan cuatro monedas en cada lado. Hay dos posibilidades:

1. Un lado es más pesado que el otro. Si este es el caso, retira tres monedas del lado más pesado, mueve tres monedas del lado más liviano al lado más pesado y coloca tres monedas que no se pesaron la primera vez en el lado más liviano. (Recuerda qué monedas son cuáles). Hay tres posibilidades:

1.a) El lado que pesaba más la primera vez sigue siendo más pesado. Esto significa que la moneda que quedó en ese lado es más pesada o que la moneda que quedó en el lado más liviano es más liviana. Al equilibrar una de estas monedas con una de las otras diez, se revela cuál de estas dos es la verdadera, y así se resuelve el acertijo.

1.b) El lado que era más pesado la primera vez es más liviano la segunda vez. Esto significa que una de las tres monedas que pasaron del lado más liviano al más pesado es la moneda liviana. Para el tercer intento, se pesan dos de estas monedas una contra la otra: si una es más liviana, es la única moneda; si se equilibran, la tercera moneda es la liviana.

1.c) Ambos lados son iguales. Esto significa que una de las tres monedas que se retiró del lado más pesado es la moneda pesada. Para el tercer intento, se pesan dos de estas monedas una contra la otra: si una es más pesada, es la única moneda; si se equilibran, la tercera moneda es la pesada.

2. Ambos lados son iguales. Si este es el caso, las ocho monedas son idénticas y se pueden dejar de lado. Tome las cuatro monedas restantes y coloque tres en un lado de la balanza. Coloque 3 de las 8 monedas idénticas en el otro lado. Hay tres posibilidades:

2.a) Las tres monedas restantes son más livianas. En este caso, ahora sabes que una de esas tres monedas es la que no está en la balanza y que es más liviana. Toma dos de esas tres monedas y pésalas una contra la otra. Si la balanza se inclina, entonces la moneda más liviana es la que no está en la balanza. Si las dos monedas se equilibran, entonces la tercera moneda que no está en la balanza es la que no está en la balanza y es más liviana.

2.b) Las tres monedas restantes son más pesadas. En este caso, ahora sabes que una de esas tres monedas es la que no está en la balanza y que es más pesada. Toma dos de esas tres monedas y pésalas una contra la otra. Si la balanza se inclina, entonces la moneda más pesada es la que no está en la balanza. Si las dos monedas se equilibran, entonces la tercera moneda que no está en la balanza es la que no está en la balanza y es más pesada.

2.c) Las tres monedas restantes se equilibran. En este caso, solo hay que pesar la moneda restante contra cualquiera de las otras 11 monedas y esto nos indica si es más pesada, más liviana o igual.

Variaciones

Dada una población de 13 monedas en la que se sabe que 1 de las 13 es diferente (masa) del resto, es sencillo determinar de qué moneda se trata con una balanza y 3 pruebas de la siguiente manera:

1) Subdivide las monedas en 2 grupos de 4 monedas y un tercer grupo con las 5 monedas restantes.

2) Prueba 1, Pruebe los 2 grupos de 4 monedas entre sí:

a. Si las monedas están equilibradas, la moneda impar está en la población de 5 y procedemos a la prueba 2a.

b. La moneda impar se encuentra entre la población de 8 monedas, proceda de la misma manera que en el problema de las 12 monedas.

3) Prueba 2a, Pruebe 3 de las monedas del grupo de 5 monedas contra 3 monedas cualesquiera de la población de 8 monedas:

a. Si las 3 monedas están en equilibrio, entonces la moneda impar se encuentra entre las 2 monedas restantes. Pruebe una de las 2 monedas con cualquier otra moneda; si están en equilibrio, la moneda impar es la última moneda no probada; si no están en equilibrio, la moneda impar es la moneda de prueba actual.

b. Si las 3 monedas no se equilibran, entonces la moneda impar es de esta población de 3 monedas. Preste atención a la dirección de la oscilación de la balanza (hacia arriba significa que la moneda impar es liviana, hacia abajo significa que es pesada). Retire una de las 3 monedas, mueva otra al otro lado de la balanza (retire todas las demás monedas de la balanza). Si la balanza se equilibra, la moneda impar es la moneda que se retiró. Si la balanza cambia de dirección, la moneda impar es la que se movió al otro lado, de lo contrario, la moneda impar es la moneda que permaneció en su lugar.

Con una moneda de referencia

Si hay una moneda auténtica como referencia, las monedas sospechosas pueden ser trece. Numere las monedas del 1 al 13 y la moneda auténtica con el número 0 y realice estos pesajes en cualquier orden:

• 0, 1, 4, 5, 6 contra 7, 10, 11, 12, 13
• 0, 2, 4, 10, 11 contra 5, 8, 9, 12, 13
• 0, 3, 8, 10, 12 contra 6, 7, 9, 11, 13

Si la balanza se desequilibra una sola vez, entonces debe ser una de las monedas 1, 2, 3, que sólo aparecen en una pesada. Si nunca hay equilibrio, entonces debe ser una de las monedas 10-13 que aparecen en todas las pesadas. Siempre es posible elegir la moneda falsa correspondiente a cada uno de los 27 resultados (13 monedas, una demasiado pesada o una demasiado ligera, son 26 posibilidades), excepto cuando todas las pesadas están equilibradas, en cuyo caso no hay ninguna moneda falsa (o su peso es correcto). Si se eliminan las monedas 0 y 13 de estas pesadas, dan una solución genérica al problema de las 12 monedas.

Si dos monedas son falsas, este procedimiento, en general, no selecciona ninguna de ellas, sino alguna moneda auténtica. Por ejemplo, si las monedas 1 y 2 son falsas, se selecciona incorrectamente la moneda 4 o la 5.

Sin moneda de referencia

En una variante relajada de este rompecabezas, uno solo necesita encontrar la moneda falsa sin necesariamente poder determinar su peso en relación con las demás. En este caso, claramente cualquier solución que previamente haya pesado todas las monedas en algún momento puede adaptarse para manejar una moneda adicional. Esta moneda nunca se coloca en la balanza, pero si se equilibran todos los pesos, se elige como la moneda falsa. No es posible hacerlo mejor, ya que a cualquier moneda que se coloque en la balanza en algún momento y se elija como moneda falsa, siempre se le puede asignar un peso en relación con las demás.

Un método que pesa los mismos conjuntos de monedas independientemente de los resultados permite:

1. (entre 12 monedas A–L) concluya si todas pesan lo mismo, o encuentre la moneda extraña y diga si es más liviana o más pesada, o
2. (entre 13 monedas A–M) encuentre la moneda impar y, con una probabilidad de 12/13, indique si es más liviana o más pesada (para la probabilidad restante de 1/13, solo que sea diferente).

Los tres resultados posibles de cada pesaje se pueden denotar con "\" para el lado izquierdo que es más ligero, "/" para el lado derecho que es más ligero y "–" para ambos lados que tienen el mismo peso. Los símbolos para los pesajes se enumeran en secuencia. Por ejemplo, "//–" significa que el lado derecho es más ligero en el primer y segundo pesaje, y ambos lados pesan lo mismo en el tercer pesaje. Tres pesajes dan los siguientes resultados 3 ³ = 27. A excepción de "–––", los conjuntos se dividen de manera que cada conjunto de la derecha tiene una "/" donde el conjunto de la izquierda tiene una "\", y viceversa:

/// \\\\// /\\/\/ \/\//\ \\/\/– /\––\/ –/\/–\ \–/\\– //––\\ –//\–\ /–//–– \–––/– –\–––/ ––\–––

Como cada pesaje da un resultado significativo solo cuando el número de monedas del lado izquierdo es igual al número del lado derecho, ignoramos la primera fila, de modo que cada columna tiene el mismo número de símbolos "\" y "/" (cuatro de cada uno). Las filas están etiquetadas, el orden de las monedas es irrelevante:

\// Una luz /\\ Una pesada/\/ B ligero \/\ B pesado//\ C ligero \\/ C pesado\/– D ligero /\– D pesado–\/ E ligero –/\ E pesado/–\ F ligero \–/ F pesado\\– G ligero //– G pesado–\\ H ligero –// H pesado\–\ Yo ligero /–/ Yo pesado/–– J ligero \–– J pesado–/– K ligero –\– K pesado––/ L ligero ––\ L pesado––– M más ligero o más pesado (estuche para 13 monedas), o todas las monedas pesan lo mismo (estuche de 12 monedas)

Utilizando el patrón de resultados anterior, se puede determinar la composición de las monedas para cada pesaje; por ejemplo, el conjunto "\/– D light" implica que la moneda D debe estar en el lado izquierdo en el primer pesaje (para hacer que ese lado sea más claro), en el lado derecho en el segundo y sin usar en el tercero:

1er pesaje: lado izquierdo: ADGI, lado derecho: BCFJ2º pesaje: lado izquierdo: BEGH, lado derecho: ACDK3er pesaje: lado izquierdo: CFHI, lado derecho: ABEL

Los resultados se leen en la tabla. Por ejemplo, si el lado derecho es más ligero en las dos primeras pesadas y ambos lados pesan lo mismo en la tercera, el código correspondiente "//– G pesado" implica que la moneda G es la impar y es más pesada que las demás. ^[5]

Generalización a múltiples escalas

En otra generalización de este problema, tenemos dos balanzas que se pueden utilizar en paralelo. Por ejemplo, si sabes exactamente que una moneda es diferente pero no sabes si es más pesada o más liviana que una moneda normal, entonces, en rondas, puedes resolver el problema con un máximo de monedas. ^[6] ${\displaystyle n}$ ${\displaystyle (5^{n}-5)/2}$

Generalización a múltiples monedas desconocidas

La generalización de este problema se describe en Chudnov. ^[7]

Sea el espacio euclidiano -dimensional y sea el producto interno de los vectores y de Para vectores y subconjuntos las operaciones y se definen, respectivamente, como  ; , , Por denotaremos el [−1; 1]-cubo discreto en ; es decir, el conjunto de todas las secuencias de longitud sobre el alfabeto El conjunto es la bola discreta de radio (en la métrica de Hamming ) con centro en el punto Los pesos relativos de los objetos se dan por un vector que define las configuraciones de pesos de los objetos: el objeto n tiene peso estándar si el peso del objeto n es mayor (menor) por un valor constante (desconocido) si (respectivamente, ). El vector caracteriza los tipos de objetos: el tipo estándar, el tipo no estándar (es decir, configuraciones de tipos), y no contiene información sobre los pesos relativos de los objetos no estándar. ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle n}$ ${\displaystyle [\mathrm {e} ^{1},\mathrm {e} ^{2}]}$ ${\displaystyle \mathrm {e} ^{1}}$ ${\displaystyle \mathrm {e} ^{2}}$ ${\displaystyle \mathbb {R} ^{n}.}$ ${\displaystyle \mathrm {e} =(e_{1},\dots ,e_{n})\in \mathbb {R} ^{n}}$ ${\displaystyle E=\{\mathrm {e} ^{j}\}\subseteq \mathbb {R} ^{n},}$ ${\displaystyle (\cdot )^{*}}$ ${\displaystyle (\cdot )^{+}}$ ${\displaystyle \mathrm {e} ^{*}=(sign(e_{i}))_{i}}$ ${\displaystyle E^{*}=\{(\mathrm {e} ^{j})^{*}\}}$ ${\displaystyle \mathrm {e} ^{+}=(|sign(e_{i})|)_{i}}$ ${\displaystyle E^{+}=\{(\mathrm {e} ^{j})^{+}\}.}$ ${\displaystyle I^{n}}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle n}$ ${\displaystyle I=\{-1,0,1\}}$ ${\displaystyle I_{t}^{n}=\{\mathrm {x} \in I^{n}|w(\mathrm {x} )\leq t\}\subseteq I^{n}}$ ${\displaystyle t}$ ${\displaystyle w()}$ ${\displaystyle \mathrm {0} .}$ ${\displaystyle n}$ ${\displaystyle \mathrm {x} =(x_{1},\dots ,x_{n})\in I^{n},}$ ${\displaystyle i}$ ${\displaystyle x_{i}=0;}$ ${\displaystyle i}$ ${\displaystyle x_{i}=1}$ ${\displaystyle x_{i}=-1}$ ${\displaystyle \mathrm {x} ^{+}}$

Un pesaje (una comprobación) se da por un vector el resultado de un pesaje para una situación es El pesaje dado por un vector tiene la siguiente interpretación: para una comprobación dada el objeto º participa en el pesaje si ; se coloca en el platillo izquierdo de la balanza si y se coloca en el platillo derecho si Para cada pesaje , ambos platillos deben contener el mismo número de objetos: si en algún platillo el número de objetos es menor de lo que debería ser, entonces recibe algunos objetos de referencia. El resultado de un pesaje describe los siguientes casos: la balanza si , el platillo izquierdo pesa más que el derecho si , y el platillo derecho pesa más que el izquierdo si La incompletitud de la información inicial sobre la distribución de pesos de un grupo de objetos se caracteriza por el conjunto de distribuciones admisibles de pesos de objetos que también se llama conjunto de situaciones admisibles, los elementos de se llaman situaciones admisibles. ${\displaystyle \mathrm {h} \in I^{n};}$ ${\displaystyle \mathrm {x} \in I^{n}}$ ${\displaystyle s(\mathrm {x} ;\mathrm {h} )=sign([\mathrm {x} ;\mathrm {h} ]).}$ ${\displaystyle \mathrm {h} =(h_{1},\dots ,h_{n})}$ ${\displaystyle i}$ ${\displaystyle h_{i}\neq 0}$ ${\displaystyle h_{i}<0}$ ${\displaystyle h_{i}>0.}$ ${\displaystyle \mathrm {h} }$ ${\displaystyle r(\mathrm {h} )=[\mathrm {h} ;1,\dots ,1]}$ ${\displaystyle s(\mathrm {x} ;\mathrm {h} )}$ ${\displaystyle s(\mathrm {x} ;\mathrm {h} )=0}$ ${\displaystyle s(\mathrm {x} ;\mathrm {h} )=-1}$ ${\displaystyle s(\mathrm {x} ;\mathrm {h} )=1.}$ ${\displaystyle Z\subseteq I^{n},}$ ${\displaystyle z\in Z}$

Cada ponderación induce la partición del conjunto por el plano ( hiperplano ) en tres partes , y define la partición correspondiente del conjunto donde ${\displaystyle \mathrm {h} }$ ${\displaystyle I^{n}}$ ${\displaystyle [\mathrm {x} ;\mathrm {h} ]=0}$ ${\displaystyle W(s|I^{n};\mathrm {h} )=\{\mathrm {x} \in I^{n}|s(\mathrm {x} ;\mathrm {h} )=s\}}$ ${\displaystyle s\in I,}$ ${\displaystyle Z=W(0|Z,\mathrm {h} )+W(1|Z,\mathrm {h} )+W(-1|Z,\mathrm {h} ),}$ ${\displaystyle W(s|Z,\mathrm {h} )=W(s|I^{n},\mathrm {h} )\cap Z.}$

Definición 1. Un algoritmo de ponderación (WA) de longitud es una secuencia donde es la función que determina la comprobación en cada paso del algoritmo a partir de los resultados de las ponderaciones en los pasos anteriores ( es una comprobación inicial dada). ${\displaystyle {\mathcal {A}}}$ ${\displaystyle m}$ ${\displaystyle {\mathcal {A}}=<\mathrm {A} _{1},\dots ,\mathrm {A} _{m}>,}$ ${\displaystyle \mathrm {A} _{j}:I^{j-1}\to I^{n}}$ ${\displaystyle \mathrm {h} ^{j}=\mathrm {A} _{j}(s^{j-1});\mathrm {h} ^{j}\in I^{n},}$ ${\displaystyle j}$ ${\displaystyle j=1,2,\dots ,m,}$ ${\displaystyle \mathrm {s} ^{j-1}=(s_{1},\dots ,s_{j-1})\in I^{j-1}}$ ${\displaystyle \mathrm {h} ^{1}=\mathrm {A} _{1}()}$

Sea el conjunto de todos los -síndromes y el conjunto de situaciones con el mismo síndrome ; es decir, ; ${\displaystyle S(Z,{\mathcal {A}})}$ ${\displaystyle (Z,{\mathcal {A}})}$ ${\displaystyle W(s|{\mathcal {A}})\subseteq I}$ ${\displaystyle s}$ ${\displaystyle W(s|{\mathcal {A}})=\{\mathrm {z} \in I^{m}|s(z|{\mathcal {A}})=s\}}$ ${\displaystyle W(s|Z;{\mathcal {A}})=W(s|{\mathcal {A}})\cap Z.}$

Definición 2. Se dice que un WA : a) identifica las situaciones en un conjunto si la condición se cumple para todos b) identifica los tipos de objetos en un conjunto si la condición se cumple para todos ${\displaystyle {\mathcal {A}}}$ ${\displaystyle Z}$ ${\displaystyle |W(s|Z,{\mathcal {A}})|=1}$ ${\displaystyle s\in S(Z{\mathcal {A}});}$ ${\displaystyle Z}$ ${\displaystyle |W^{+}(s|Z{\mathcal {A}})|=1}$ ${\displaystyle s\in S(Z{\mathcal {A}}).}$

^{En [7]} se demuestra que para los denominados conjuntos adecuados un algoritmo de identificación de tipos identifica también las situaciones en ${\displaystyle Z}$ ${\displaystyle Z.}$

^{Como ejemplo, en [7]} se construyen algoritmos dinámicos perfectos (de dos cascadas) con parámetros que corresponden a los parámetros del código Golay ternario perfecto (código Virtakallio-Golay). Al mismo tiempo, se establece que no existe un WA estático (es decir, un código de ponderación) con los mismos parámetros. ${\displaystyle n=11,m=5,t=2}$

Cada uno de estos algoritmos, mediante 5 pesajes, encuentra entre 11 monedas hasta dos monedas falsas que pueden ser más pesadas o más ligeras que las monedas reales por el mismo valor. En este caso, el dominio de incertidumbre (el conjunto de situaciones admisibles) contiene situaciones, es decir, el WA construido se encuentra en el límite de Hamming y , en este sentido, es perfecto. ${\displaystyle 1+2C_{11}^{1}+2^{2}C_{11}^{2}=3^{5}}$ ${\displaystyle t=2}$

Hasta la fecha no se sabe si existen otros WA perfectos que identifiquen las situaciones en para algunos valores de . Además, no se sabe si para algunos existen soluciones para la ecuación (correspondiente a la cota de Hamming para códigos ternarios) que es, obviamente, necesaria para la existencia de un WA perfecto. Solo se sabe que para no hay WA perfectos, y para esta ecuación tiene la única solución no trivial que determina los parámetros del WA perfecto construido. ${\displaystyle I_{t}^{n}}$ ${\displaystyle n,t}$ ${\displaystyle t>2}$ ${\displaystyle \sum _{i=0}^{t}2^{i}C_{n}^{i}=3^{m}}$ ${\displaystyle t=1}$ ${\displaystyle t=2}$ ${\displaystyle n=11,m=5}$

Referencias

1. Smith, CAB (febrero de 1947). "El problema de la moneda falsa". Mathematical Gazette . 31 (293): 31–39. doi :10.2307/3608991. JSTOR  3608991.
2. Grossman, Howard D. (septiembre-diciembre de 1945). "El problema de las doce monedas". Scripta Mathematica . 11 (3–4): 360–361.
3. Guy, Richard; Nowakowski, Richard (febrero de 1995). "Problemas de pesaje de monedas". The American Mathematical Monthly . 102 (2): 164–167. doi :10.1080/00029890.1995.11990553.
4. Grossman, Howard (1945). Scripta Mathematica XI .
5. "Foro de Matemáticas - Pregúntele al Dr. Math". mathforum.org . Archivado desde el original el 12 de junio de 2002.
6. Khovanova, Tanya (2013). "Solución al problema de la moneda falsa y su generalización". arXiv : 1310.7268 [math.HO].
7. Chudnov, Alexander M. (2015). "Algoritmos de ponderación de clasificación e identificación de situaciones". Matemáticas discretas y aplicaciones . 25 (2): 69–81. doi :10.1515/dma-2015-0007. S2CID  124796871.

Enlaces externos

• Un ejemplo jugable del segundo rompecabezas.
• Balanza de dos platos y problema generalizado de la moneda falsa