La ley de Paschen es una ecuación que da la tensión de ruptura , es decir, la tensión necesaria para iniciar una descarga o arco eléctrico , entre dos electrodos en un gas en función de la presión y la longitud del espacio. [2] [3] Lleva el nombre de Friedrich Paschen , quien la descubrió empíricamente en 1889. [4]
Paschen estudió el voltaje de ruptura de varios gases entre placas metálicas paralelas a medida que variaban la presión del gas y la distancia entre ellas:
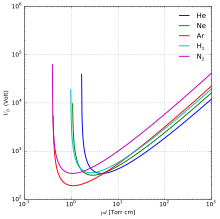
Para un gas dado, el voltaje es una función únicamente del producto de la presión por la longitud del espacio libre. [2] [3] La curva que encontró de voltaje versus el producto de la presión por la longitud del espacio libre (derecha) se llama curva de Paschen . Encontró una ecuación que se ajusta a estas curvas, que ahora se llama ley de Paschen. [3]
A presiones y longitudes de espacio mayores, el voltaje de ruptura es aproximadamente proporcional al producto de la presión y la longitud del espacio, y a veces se utiliza el término ley de Paschen para referirse a esta relación más simple. [5] Sin embargo, esto solo es aproximadamente cierto, en un rango limitado de la curva.
Los primeros experimentadores de vacío descubrieron un comportamiento bastante sorprendente. A veces, un arco se formaba en una trayectoria irregular y larga en lugar de a la distancia mínima entre los electrodos. Por ejemplo, en el aire, a una presión de una atmósfera , la distancia para la tensión de ruptura mínima es de aproximadamente 7,5 μm. La tensión necesaria para formar un arco a esta distancia es de 327 V, que es insuficiente para encender los arcos en espacios que son más anchos o más estrechos. Para un espacio de 3,5 μm, la tensión necesaria es de 533 V, casi el doble. Si se aplicaran 500 V, no sería suficiente para formar un arco a la distancia de 2,85 μm, pero sí a una distancia de 7,5 μm.
Paschen descubrió que el voltaje de ruptura se describía mediante la ecuación [1]
donde es el voltaje de ruptura en voltios , es la presión en pascales , es la distancia de separación en metros , es el coeficiente de emisión de electrones secundarios (la cantidad de electrones secundarios producidos por ion positivo incidente), es la ionización de saturación en el gas a un ( campo eléctrico /presión) particular, y está relacionado con las energías de excitación e ionización.
Las constantes y se interpolan en el primer coeficiente de Townsend . Se determinan experimentalmente y se ha descubierto que son aproximadamente constantes en un rango restringido de para cualquier gas dado. Por ejemplo, el aire con una en el rango de 450 a 7500 V/(kPa·cm), = 112,50 (kPa·cm) −1 y = 2737,50 V/(kPa·cm). [6]
La gráfica de esta ecuación es la curva de Paschen. Al derivarla con respecto a y poner la derivada a cero, se puede encontrar el voltaje mínimo. Esto da
y predice la ocurrencia de un voltaje de ruptura mínimo para = 7,5×10 −6 m·atm. Esto es 327 V en el aire a presión atmosférica estándar a una distancia de 7,5 μm.
La composición del gas determina tanto el voltaje mínimo del arco como la distancia a la que se produce. Para el argón , el voltaje mínimo del arco es de 137 V a un diámetro mayor de 12 μm. Para el dióxido de azufre , el voltaje mínimo del arco es de 457 V a solo 4,4 μm.
Para el aire en condiciones estándar de temperatura y presión (STP), el voltaje necesario para formar un arco en un espacio de 1 metro es de aproximadamente 3,4 MV. [7] Por lo tanto, la intensidad del campo eléctrico para este espacio es de 3,4 MV/m.
El campo eléctrico necesario para generar un arco a través del espacio de voltaje mínimo es mucho mayor que el necesario para generar un arco a través de un espacio de un metro. En espacios grandes (o con una gran desviación estándar), se sabe que la Ley de Paschen falla. El Criterio de Meek para la ruptura se utiliza generalmente para espacios grandes. [8] Tiene en cuenta la falta de uniformidad en el campo eléctrico y la formación de corrientes de vapor debido a la acumulación de carga dentro del espacio que puede ocurrir a grandes distancias. Para un espacio de 7,5 μm, el voltaje del arco es de 327 V, que es de 43 MV/m. Esto es aproximadamente 14 veces mayor que la intensidad del campo para el espacio de 1,5 metros. El fenómeno está bien verificado experimentalmente y se lo conoce como el mínimo de Paschen.
La ecuación pierde precisión para espacios de menos de 10 μm en el aire a una atmósfera [9] y predice incorrectamente un voltaje de arco infinito en un espacio de aproximadamente 2,7 micrómetros. El voltaje de ruptura también puede diferir de la predicción de la curva de Paschen para espacios entre electrodos muy pequeños, cuando la emisión de campo desde la superficie del cátodo se vuelve importante.
El recorrido libre medio de una molécula en un gas es la distancia media entre su colisión con otras moléculas. Esto es inversamente proporcional a la presión del gas, dada la temperatura constante. En el aire a STP el recorrido libre medio de las moléculas es de unos 96 nm. Como los electrones son mucho más pequeños, su distancia media entre colisiones con moléculas es unas 5,6 veces mayor, o unos 0,5 μm. Esta es una fracción sustancial de la separación de 7,5 μm entre los electrodos para un voltaje de arco mínimo. Si el electrón está en un campo eléctrico de 43 MV/m, se acelerará y adquirirá 21,5 eV de energía en 0,5 μm de recorrido en la dirección del campo. La primera energía de ionización necesaria para desalojar un electrón de una molécula de nitrógeno es de unos 15,6 eV. El electrón acelerado adquirirá energía más que suficiente para ionizar una molécula de nitrógeno. Este electrón liberado se acelerará a su vez, lo que provocará otra colisión. Una reacción en cadena conduce entonces a una ruptura por avalancha y se produce un arco a partir de la cascada de electrones liberados. [10]
En un gas con mayor presión, se producirán más colisiones en el camino de los electrones entre los electrodos. Cuando el producto presión-brecha es alto, un electrón colisionará con muchas moléculas de gas diferentes a medida que viaja desde el cátodo hasta el ánodo. Cada una de las colisiones aleatoriza la dirección del electrón, por lo que el electrón no siempre es acelerado por el campo eléctrico ; a veces viaja de regreso hacia el cátodo y es desacelerado por el campo.
Las colisiones reducen la energía del electrón y hacen que le resulte más difícil ionizar una molécula. Las pérdidas de energía por un mayor número de colisiones requieren voltajes mayores para que los electrones acumulen suficiente energía para ionizar muchas moléculas de gas, lo que se requiere para producir una ruptura por avalancha .
En el lado izquierdo del mínimo de Paschen, el producto es pequeño. El camino libre medio de los electrones puede llegar a ser largo en comparación con el espacio entre los electrodos. En este caso, los electrones pueden ganar grandes cantidades de energía, pero tienen menos colisiones ionizantes. Por lo tanto, se requiere un mayor voltaje para asegurar la ionización de suficientes moléculas de gas para iniciar una avalancha.
Para calcular la tensión de ruptura se supone un campo eléctrico homogéneo. Este es el caso de una configuración de condensador de placas paralelas . Los electrodos pueden tener la distancia . El cátodo se encuentra en el punto .
Para obtener la ionización por impacto , la energía de los electrones debe ser mayor que la energía de ionización de los átomos de gas entre las placas. Por cada longitud de trayectoria se producirán varias ionizaciones. se conoce como el primer coeficiente de Townsend, ya que fue introducido por Townsend. [11] El aumento de la corriente de electrones se puede describir para la configuración supuesta como
(Por lo tanto, la cantidad de electrones libres en el ánodo es igual a la cantidad de electrones libres en el cátodo que se multiplicaron por la ionización por impacto. Cuanto mayor sea y/o menor , más electrones libres se crean).
El número de electrones creados es
Despreciando las posibles ionizaciones múltiples del mismo átomo, el número de iones creados es el mismo que el número de electrones creados:
es la corriente de iones. Para que la descarga continúe, se deben crear electrones libres en la superficie del cátodo. Esto es posible porque los iones que golpean el cátodo liberan electrones secundarios en el impacto. (Para voltajes aplicados muy grandes también puede ocurrir emisión de electrones de campo ). Sin emisión de campo, podemos escribir
donde es el número medio de electrones secundarios generados por ion. Esto también se conoce como el segundo coeficiente de Townsend. Suponiendo que , se obtiene la relación entre los coeficientes de Townsend al poner ( 4 ) en ( 3 ) y transformar:
¿Cuál es la cantidad de ? El número de ionización depende de la probabilidad de que un electrón choque contra una molécula de gas. Esta probabilidad es la relación entre el área de la sección transversal de una colisión entre un electrón y un ion y el área total disponible para que el electrón la atraviese:
Como lo expresa la segunda parte de la ecuación, también es posible expresar la probabilidad como relación entre el camino recorrido por el electrón y el camino libre medio (distancia a la que ocurre otra colisión).

es el número de moléculas que pueden alcanzar los electrones. Se puede calcular utilizando la ecuación de estado del gas ideal.
El esquema adjunto ilustra que . Como el radio de un electrón se puede despreciar en comparación con el radio de un ion, se simplifica a . Usando esta relación, poniendo ( 7 ) en ( 6 ) y transformando a uno se obtiene
donde el factor sólo se introdujo para una mejor visión general.
La alteración de la corriente de electrones que aún no han colisionado en cada punto del camino se puede expresar como
Esta ecuación diferencial se puede resolver fácilmente:
La probabilidad de que (aún no haya habido una colisión en el punto ) es
Según su definición es el número de ionizaciones por longitud de camino y por tanto la relación de la probabilidad de que no haya habido colisión en el camino libre medio de los iones, y el camino libre medio de los electrones:
Se consideró que la energía que una partícula cargada puede obtener entre una colisión depende de la intensidad del campo eléctrico y de la carga :
Para el condensador de placas paralelas tenemos , donde es el voltaje aplicado. Como se supuso que una sola ionización es la carga elemental . Ahora podemos poner ( 13 ) y ( 8 ) en ( 12 ) y obtener
Poniendo esto en (5) y transformando en obtenemos la ley de Paschen para el voltaje de ruptura que fue investigada por primera vez por Paschen en [4] y cuya fórmula fue derivada por primera vez por Townsend en [12].
La ignición de plasma en la definición de Townsend ( descarga de Townsend ) es una descarga autosostenida, independiente de una fuente externa de electrones libres. Esto significa que los electrones del cátodo pueden llegar al ánodo a distancia e ionizar al menos un átomo en su camino. Por lo que según la definición de esta relación debe cumplirse:
Si se utiliza en lugar de ( 5 ) se obtiene el voltaje de ruptura
La ley de Paschen exige que:
Los distintos gases tendrán distintos recorridos libres medios para las moléculas y los electrones. Esto se debe a que las distintas moléculas tienen secciones eficaces de ionización, es decir, diferentes diámetros efectivos. Los gases nobles como el helio y el argón son monoatómicos , lo que los hace más difíciles de ionizar y tienden a tener diámetros efectivos más pequeños. Esto les da mayores recorridos libres medios.
Los potenciales de ionización difieren entre las moléculas, así como la velocidad con la que recuperan electrones después de que han sido expulsados de su órbita. Los tres efectos cambian el número de colisiones necesarias para provocar un crecimiento exponencial de los electrones libres. Estos electrones libres son necesarios para provocar un arco.