En informática , los minifloats son valores de punto flotante representados con muy pocos bits . Esta precisión reducida los hace inadecuados para cálculos numéricos de propósito general, pero son útiles para propósitos especiales como:
Además, se utilizan frecuentemente como herramienta pedagógica en cursos de informática para demostrar las propiedades y estructuras de la aritmética de punto flotante y los números IEEE 754 .
Los minifloats con 16 bits son números de precisión media (a diferencia de los de precisión simple y doble ). También hay minifloats con 8 bits o incluso menos. [2]
Los minifloats pueden diseñarse siguiendo los principios del estándar IEEE 754. En este caso deben obedecer las reglas (no escritas explícitamente) para la frontera entre números normales y subnormales y deben tener patrones especiales para infinito y NaN . Los números normalizados se almacenan con un exponente sesgado . La nueva revisión del estándar, IEEE 754-2008 , tiene minifloats binarios de 16 bits .
Un minifloat generalmente se describe utilizando una tupla de cuatro números ( S , E , M , B ):
Por lo tanto, un formato minifloat denotado por ( S , E , M , B ) tiene una longitud de S + E + M bits. La notación ( S , E , M , B ) se puede convertir a un formato ( B , P , L , U ) como (2, M + 1, B + 1, 2 S − B ) (con uso IEEE de exponentes).
Aquí se muestra un minifloat de 1 byte (8 bits) con 1 bit de signo, 4 bits de exponente y 3 bits de significando (en resumen, un minifloat 1.4.3). El sesgo del exponente se define como 7 para centrar los valores alrededor de 1 para que coincidan con otros flotantes IEEE 754 [3] [4] por lo que (para la mayoría de los valores) el multiplicador real para el exponente x es 2 x −7 . Todos los principios IEEE 754 deberían ser válidos. [5]
Los números en una base diferente se marcan como ... base , por ejemplo, 101 2 = 5. Los patrones de bits tienen espacios para visualizar sus partes.
El cero se representa como exponente cero con una mantisa cero. El exponente cero significa que cero es un número subnormal con un prefijo "0" inicial y con la mantisa cero todos los bits después del punto decimal son cero, lo que significa que este valor se interpreta como . Los números de punto flotante usan un cero con signo , por lo que también está disponible y es igual a positivo .
0 0000 000 = 01 0000 000 = −0
El significado se amplía con "0" y el valor del exponente se trata como 1 más alto, como el número menos normalizado:
0 0000 001 = 0,001 2 × 2 1 - 7 = 0,125 × 2 -6 = 0,001953125 (número menos subnormal)...0 0000 111 = 0,111 2 × 2 1 - 7 = 0,875 × 2 -6 = 0,013671875 (mayor número subnormal)
El significado se amplía con "1":
0 0001 000 = 1,000 2 × 2 1 - 7 = 1 × 2 -6 = 0,015625 (número menos normalizado)0 0001 001 = 1,001 2 × 2 1 - 7 = 1,125 × 2 -6 = 0,017578125...0 0111 000 = 1.000 2 × 2 7 - 7 = 1 × 2 0 = 10 0111 001 = 1,001 2 × 2 7 - 7 = 1,125 × 2 0 = 1,125 (valor menor por encima de 1)...0 1110 000 = 1.000 2 × 2 14 - 7 = 1.000 × 2 7 = 1280 1110 001 = 1,001 2 × 2 14 - 7 = 1,125 × 2 7 = 144...0 1110 110 = 1,110 2 × 2 14 - 7 = 1,750 × 2 7 = 2240 1110 111 = 1,111 2 × 2 14 - 7 = 1,875 × 2 7 = 240 (mayor número normalizado)
Los valores infinitos tienen el exponente más alto, con la mantisa establecida en cero. El bit de signo puede ser positivo o negativo.
0 1111 000 = +infinito1 1111 000 = −infinito
Los valores NaN tienen el exponente más alto, con un valor distinto de cero para la mantisa. Un flotante con signo de 1 bit y mantisa de 3 bits tiene valores NaN.
s 1111 mmm = NaN (si mmm ≠ 000)
Este es un gráfico de todos los valores posibles para este ejemplo de flotante de 8 bits.
Solo hay 242 valores diferentes que no son NaN (si +0 y −0 se consideran diferentes), porque 14 de los patrones de bits representan NaN.
En estos tamaños pequeños, otros valores de sesgo pueden ser interesantes; por ejemplo, un sesgo de -2 hará que los números del 0 al 16 tengan la misma representación de bits que los enteros del 0 al 16, con la pérdida de que no se pueden representar valores no enteros.
0 0000 000 = 0,000 2 × 2 1 - (-2) = 0,0 × 2 3 = 0 (número subnormal)0 0000 001 = 0,001 2 × 2 1 - (-2) = 0,125 × 2 3 = 1 (número subnormal)0 0000 111 = 0,111 2 × 2 1 - (-2) = 0,875 × 2 3 = 7 (número subnormal)0 0001 000 = 1.000 2 × 2 1 - (-2) = 1.000 × 2 3 = 8 (número normalizado)0 0001 111 = 1,111 2 × 2 1 - (-2) = 1,875 × 2 3 = 15 (número normalizado)0 0010 000 = 1.000 2 × 2 2 - (-2) = 1.000 × 2 4 = 16 (número normalizado)
Lo anterior describe un ejemplo de un flotante de 8 bits con 1 bit de signo, 4 bits de exponente y 3 bits de mantisa, lo que constituye un buen equilibrio. Sin embargo, es posible asignar cualquier bit. Un formato podría optar por dar más bits al exponente si necesita un rango dinámico más amplio con menos precisión, o dar más bits a la mantisa si necesita más precisión con un rango dinámico más reducido. En el extremo, es posible asignar todos los bits al exponente, o todos menos uno de los bits a la mantisa, dejando al exponente con un solo bit. Al exponente se le debe dar al menos un bit, o de lo contrario ya no tiene sentido como flotante, simplemente se convierte en un número con signo .
Aquí se muestra un cuadro de todos los valores posibles para un número flotante de 8 bits con 1 bit de signo, 3 bits de exponente y 4 bits de significancia. Tener 1 bit de significancia más que bits de exponente garantiza que la precisión se mantenga al menos en 0,5 en todo el rango. [6]
Se pueden generar tablas como la anterior para cualquier combinación de valores SEMB (signo, exponente, mantisa/significante y sesgo) utilizando un script en Python o en GDScript.
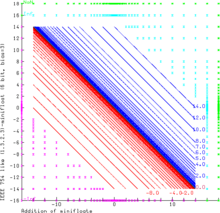
El gráfico demuestra la adición de minifloats (1.3.2.3) aún más pequeños con 6 bits. Este sistema de punto flotante sigue exactamente las reglas de IEEE 754. NaN como operando produce siempre resultados NaN. Inf − Inf y (−Inf) + Inf también dan como resultado NaN (área verde). Inf se puede aumentar y decrementar con valores finitos sin cambios. Las sumas con operandos finitos pueden dar un resultado infinito (es decir, 14.0 + 3.0 = +Inf como resultado es el área cian, −Inf es el área magenta). El rango de los operandos finitos se completa con las curvas x + y = c , donde c es siempre uno de los valores float representables (azul y rojo para resultados positivos y negativos respectivamente).
Las demás operaciones aritméticas se pueden ilustrar de forma similar:
Las GPU Radeon R300 y R420 usaban un formato de punto flotante "fp24" con 7 bits de exponente y 16 bits (+1 implícito) de mantisa. [7] "Full Precision" en Direct3D 9.0 es un formato propietario de punto flotante de 24 bits. La API gráfica D3D9 (Shader Model 2.0) de Microsoft inicialmente admitía tanto FP24 (como en el chip R300 de ATI) como FP32 (como en el chip NV30 de Nvidia) como "Full Precision", así como FP16 como "Partial Precision" para los cálculos de sombreado de vértices y píxeles realizados por el hardware gráfico.
Khronos define formatos de punto flotante de 10 y 11 bits para su uso con Vulkan. Ambos formatos no tienen bit de signo y tienen un exponente de 5 bits. El formato de 10 bits tiene una mantisa de 5 bits y el formato de 11 bits tiene una mantisa de 6 bits. [8] [9]
El grupo de trabajo P3109 de IEEE SA está trabajando actualmente en un estándar para minifloats de 8 bits optimizados para el aprendizaje automático. El borrador actual no define un formato, sino una familia de 7 formatos diferentes, llamados "binary8pP", donde "P" es un número del 1 al 7. Estos floats están diseñados para ser compactos y eficientes, pero no siguen la misma semántica que otros floats IEEE y carecen de características como el cero negativo y múltiples valores NaN. El infinito se define como el exponente y la mantisa que tienen todos unos, en lugar de otros floats IEEE donde el exponente son todos unos y la mantisa son todos ceros. [10]
El tamaño de punto flotante más pequeño posible que sigue todos los principios IEEE, incluidos los números normalizados, los números subnormales, el cero con signo, el infinito con signo y múltiples valores NaN, es un punto flotante de 4 bits con un signo de 1 bit, un exponente de 2 bits y una mantisa de 1 bit. [11] En la siguiente tabla, las columnas tienen valores diferentes para los bits de signo y mantisa, y las filas tienen valores diferentes para los bits de exponente.
Si no se requieren números normalizados, el tamaño se puede reducir a 3 bits reduciendo el exponente a 1.
En situaciones en las que se puede excluir el bit de signo, cada uno de los ejemplos anteriores se puede reducir en 1 bit más, manteniendo solo la mitad izquierda de las tablas anteriores. Un flotante de 2 bits con exponente de 1 bit y mantisa de 1 bit solo tendría valores 0, 1, Inf, NaN.
Si se permite que la mantisa sea de 0 bits, un formato de punto flotante de 1 bit tendría un exponente de 1 bit y los únicos dos valores serían 0 e Inf. El exponente debe ser de al menos 1 bit o de lo contrario ya no tendría sentido como punto flotante (sería solo un número con signo ).
Los números de punto flotante de 4 bits (sin los cuatro valores IEEE especiales) han encontrado uso para acelerar modelos de lenguaje grandes . [12]
Los minifloats también se utilizan comúnmente en dispositivos integrados, [ cita requerida ] especialmente en microcontroladores donde será necesario emular el punto flotante en el software. Para acelerar el cálculo, la mantisa normalmente ocupa exactamente la mitad de los bits, por lo que el límite del registro direcciona automáticamente las partes sin desplazarse.