En informática , un algoritmo que ignora la memoria caché (o algoritmo que trasciende la memoria caché) es un algoritmo diseñado para aprovechar la memoria caché de un procesador sin tener el tamaño de la memoria caché (o la longitud de las líneas de la memoria caché , etc.) como parámetro explícito. Un algoritmo óptimo que ignora la memoria caché es un algoritmo que utiliza la memoria caché de forma óptima (en un sentido asintótico , ignorando los factores constantes). Por lo tanto, un algoritmo que ignora la memoria caché está diseñado para funcionar bien, sin modificaciones, en varias máquinas con diferentes tamaños de memoria caché, o para una jerarquía de memoria con diferentes niveles de memoria caché que tienen diferentes tamaños. Los algoritmos que ignoran la memoria caché se contrastan con el mosaico de bucles explícito , que divide explícitamente un problema en bloques que tienen un tamaño óptimo para una memoria caché determinada.
Los algoritmos óptimos que ignoran la memoria caché son conocidos para la multiplicación de matrices , la transposición de matrices , la ordenación y varios otros problemas. Algunos algoritmos más generales, como la FFT de Cooley–Tukey , son óptimamente ignorantes de la memoria caché bajo ciertas opciones de parámetros. Como estos algoritmos solo son óptimos en un sentido asintótico (ignorando los factores constantes), puede ser necesario un ajuste adicional específico de la máquina para obtener un rendimiento casi óptimo en un sentido absoluto. El objetivo de los algoritmos que ignoran la memoria caché es reducir la cantidad de dicho ajuste que se requiere.
Por lo general, un algoritmo que ignora la memoria caché funciona mediante un algoritmo recursivo de divide y vencerás , donde el problema se divide en subproblemas cada vez más pequeños. Finalmente, se llega a un tamaño de subproblema que cabe en la memoria caché, independientemente del tamaño de la misma. Por ejemplo, una multiplicación de matrices óptima que ignora la memoria caché se obtiene dividiendo recursivamente cada matriz en cuatro submatrices que se multiplicarán, multiplicando las submatrices en profundidad . [ cita requerida ] Al ajustar para una máquina específica, se puede utilizar un algoritmo híbrido que utiliza mosaicos de bucles ajustados para los tamaños de caché específicos en el nivel inferior, pero que, por lo demás, utiliza el algoritmo que ignora la memoria caché.
La idea (y el nombre) de los algoritmos que ignoran la memoria caché fue concebida por Charles E. Leiserson en 1996 y publicada por primera vez por Harald Prokop en su tesis de maestría en el Instituto Tecnológico de Massachusetts en 1999. [1] Hubo muchos predecesores, que normalmente analizaban problemas específicos; estos se analizan en detalle en Frigo et al. 1999. Los primeros ejemplos citados incluyen Singleton 1969 para una transformada rápida de Fourier recursiva, ideas similares en Aggarwal et al. 1987, Frigo 1996 para la multiplicación de matrices y la descomposición LU, y Todd Veldhuizen 1996 para algoritmos matriciales en la biblioteca Blitz++ .
En general, se puede hacer que un programa sea más consciente del uso de caché: [2]
Los algoritmos que ignoran la memoria caché se suelen analizar utilizando un modelo idealizado de la memoria caché, a veces denominado modelo de ignorancia de la memoria caché . Este modelo es mucho más fácil de analizar que las características de una memoria caché real (que tienen asociatividad compleja, políticas de reemplazo, etc.), pero en muchos casos se puede demostrar que está dentro de un factor constante del rendimiento de una memoria caché más realista. Es diferente del modelo de memoria externa porque los algoritmos que ignoran la memoria caché no conocen el tamaño del bloque ni el tamaño de la memoria caché .
En particular, el modelo de máquina que ignora la memoria caché es una máquina abstracta (es decir, un modelo teórico de computación ). Es similar al modelo de máquina RAM que reemplaza la cinta infinita de la máquina de Turing con una matriz infinita. Se puede acceder a cada ubicación dentro de la matriz en el tiempo, de manera similar a la memoria de acceso aleatorio en una computadora real. A diferencia del modelo de máquina RAM, también introduce una caché: el segundo nivel de almacenamiento entre la RAM y la CPU. Las otras diferencias entre los dos modelos se enumeran a continuación. En el modelo de máquina que ignora la memoria caché:
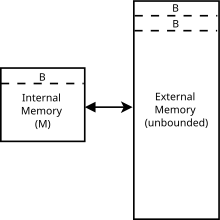
Para medir la complejidad de un algoritmo que se ejecuta dentro del modelo de ignorancia de caché, medimos la cantidad de errores de caché que experimenta el algoritmo. Debido a que el modelo captura el hecho de que acceder a los elementos en la caché es mucho más rápido que acceder a las cosas en la memoria principal , el tiempo de ejecución del algoritmo se define solo por la cantidad de transferencias de memoria entre la caché y la memoria principal. Esto es similar al modelo de memoria externa , que tiene todas las características anteriores, pero los algoritmos de ignorancia de caché son independientes de los parámetros de caché ( y ). [6] El beneficio de un algoritmo de este tipo es que lo que es eficiente en una máquina de ignorancia de caché es probable que sea eficiente en muchas máquinas reales sin realizar ajustes finos para parámetros particulares de la máquina real. Para muchos problemas, un algoritmo de ignorancia de caché óptimo también será óptimo para una máquina con más de dos niveles de jerarquía de memoria . [4]

El algoritmo más simple que ignora la memoria caché presentado en Frigo et al. es una operación de transposición de matriz fuera de lugar ( también se han ideado algoritmos en el lugar para la transposición, pero son mucho más complejos para matrices no cuadradas). Dado un arreglo A de m × n y un arreglo B de n × m , nos gustaría almacenar la transposición de A en B. La solución ingenua recorre un arreglo en orden de fila principal y otro en orden de columna principal. El resultado es que cuando las matrices son grandes, obtenemos un error de caché en cada paso del recorrido por columna. El número total de errores de caché es .
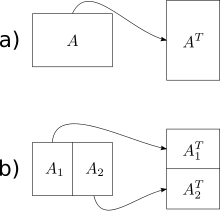
El algoritmo que ignora la memoria caché tiene una complejidad de trabajo óptima y una complejidad de caché óptima . La idea básica es reducir la transposición de dos matrices grandes en la transposición de (sub)matrices pequeñas. Para ello, dividimos las matrices por la mitad a lo largo de su dimensión más grande hasta que solo tengamos que realizar la transposición de una matriz que quepa en la memoria caché. Como el algoritmo no conoce el tamaño de la memoria caché, las matrices seguirán dividiéndose de forma recursiva incluso después de este punto, pero estas subdivisiones adicionales estarán en la memoria caché. Una vez que las dimensiones m y n sean lo suficientemente pequeñas como para que una matriz de entrada de tamaño y una matriz de salida de tamaño quepan en la memoria caché, tanto los recorridos por filas como por columnas dan como resultado errores de trabajo y de caché. Al utilizar este enfoque de dividir y vencer, podemos lograr el mismo nivel de complejidad para la matriz general.
(En principio, se podrían seguir dividiendo las matrices hasta alcanzar un caso base de tamaño 1×1, pero en la práctica se utiliza un caso base más grande (por ejemplo, 16×16) para amortizar la sobrecarga de las llamadas a subrutinas recursivas).
La mayoría de los algoritmos que ignoran la memoria caché se basan en un enfoque de "dividir y vencer". Reducen el problema de modo que, en última instancia, quepa en la memoria caché sin importar lo pequeña que sea, y finalizan la recursión en un tamaño pequeño determinado por la sobrecarga de llamadas de función y optimizaciones similares no relacionadas con la memoria caché, y luego utilizan algún patrón de acceso eficiente en el uso de la memoria caché para fusionar los resultados de estos pequeños problemas resueltos.
Al igual que la ordenación externa en el modelo de memoria externa , la ordenación sin tener en cuenta la memoria caché es posible en dos variantes: funnelsort , que se parece a mergesort ; y la ordenación por distribución sin tener en cuenta la memoria caché , que se parece a quicksort . Al igual que sus contrapartes de memoria externa, ambas alcanzan un tiempo de ejecución de , que coincide con un límite inferior y, por lo tanto, es asintóticamente óptima . [6]
Una comparación empírica de dos algoritmos basados en RAM, uno que reconoce caché y dos que no reconocen caché que implementan colas de prioridad encontró que: [7]
Otro estudio comparó tablas hash (basadas en RAM o sin memoria caché), árboles B (con memoria caché) y una estructura de datos sin memoria caché denominada "conjunto Bender". Tanto en términos de tiempo de ejecución como de uso de memoria, la tabla hash fue la mejor, seguida por el árbol B, y el conjunto Bender fue el peor en todos los casos. El uso de memoria para todas las pruebas no excedió la memoria principal. Las tablas hash se describieron como fáciles de implementar, mientras que el conjunto Bender "requirió una mayor cantidad de esfuerzo para implementarse correctamente". [8]