Consistencia local

En la satisfacción de restricciones , las condiciones de consistencia local son propiedades de los problemas de satisfacción de restricciones relacionadas con la consistencia de subconjuntos de variables o restricciones. Se pueden utilizar para reducir el espacio de búsqueda y hacer que el problema sea más fácil de resolver. Se aprovechan varios tipos de condiciones de consistencia local, incluidas la consistencia de nodos , la consistencia de arcos y la consistencia de trayectorias .

Cada condición de consistencia local puede ser impuesta por una transformación que cambia el problema sin cambiar sus soluciones; tal transformación se llama propagación de restricciones . La propagación de restricciones funciona reduciendo los dominios de las variables, fortaleciendo las restricciones o creando nuevas restricciones. Esto conduce a una reducción del espacio de búsqueda, lo que hace que el problema sea más fácil de resolver por algunos algoritmos. La propagación de restricciones también puede usarse como un verificador de insatisfacción, incompleto en general pero completo en algunos casos particulares.

Las condiciones de consistencia local se pueden agrupar en varias clases. Las condiciones de consistencia local originales requieren que cada asignación parcial consistente (de un tipo particular) pueda extenderse consistentemente a otra variable. La consistencia direccional solo requiere que esta condición se cumpla cuando la otra variable sea mayor que las de la asignación, de acuerdo con un orden determinado. La consistencia relacional incluye extensiones a más de una variable, pero esta extensión solo se requiere para satisfacer una restricción o un conjunto de restricciones determinados.

Supuestos

En este artículo, un problema de satisfacción de restricciones se define como un conjunto de variables, un conjunto de dominios y un conjunto de restricciones. Las variables y los dominios están asociados: el dominio de una variable contiene todos los valores que la variable puede tomar. Una restricción se compone de una secuencia de variables, llamada su ámbito, y un conjunto de sus evaluaciones, que son las evaluaciones que satisfacen la restricción.

Se supone que los problemas de satisfacción de restricciones a los que se hace referencia en este artículo están en una forma especial. Un problema está en forma normalizada o en forma regular si cada secuencia de variables es el ámbito de, como máximo, una restricción o exactamente una restricción. La suposición de regularidad realizada solo para restricciones binarias conduce a la forma estandarizada . Estas condiciones siempre se pueden hacer cumplir combinando todas las restricciones sobre una secuencia de variables en una sola y/o añadiendo una restricción que se cumpla para todos los valores de una secuencia de variables.

En las figuras utilizadas en este artículo, la falta de vínculos entre dos variables indica que no existe ninguna restricción o que existe una restricción satisfecha por todos los valores entre esas dos variables. ^{[ aclaración necesaria ]}

Consistencia local

Las condiciones de consistencia local "estándar" requieren que todas las evaluaciones parciales consistentes puedan extenderse a otra variable de tal manera que la asignación resultante sea consistente. Una evaluación parcial es consistente si satisface todas las restricciones cuyo alcance es un subconjunto de las variables asignadas. ^{[ aclaración necesaria ]}

Consistencia de nodos

La consistencia de los nodos requiere que cada restricción unaria de una variable sea satisfecha por todos los valores en el dominio de la variable, y viceversa. Esta condición se puede aplicar de manera trivial reduciendo el dominio de cada variable a los valores que satisfacen todas las restricciones unarias de esa variable. Como resultado, las restricciones unarias se pueden ignorar y asumir que están incorporadas en los dominios.

Por ejemplo, dada una variable con un dominio de y una restricción , la consistencia del nodo restringiría el dominio a y la restricción podría entonces descartarse. Este paso de preprocesamiento simplifica las etapas posteriores. ${\displaystyle V}$ ${\displaystyle \left\{1,2,3,4\right\}}$ ${\displaystyle V\leq 3}$ ${\displaystyle \left\{1,2,3\right\}}$

Consistencia del arco

${\displaystyle x_{2}}$es consistente con pero no con , ya que el valor no es compatible con ningún valor para . ${\displaystyle x_{3}}$ ${\displaystyle x_{1}}$ ${\displaystyle x_{2}=1}$ ${\displaystyle x_{1}}$

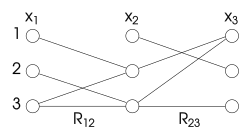
Una variable de un problema de satisfacción de restricciones es arcoconsistente con otra si cada uno de sus valores admisibles es consistente con algún valor admisible de la segunda variable. Formalmente, una variable es arcoconsistente con otra variable si, para cada valor en el dominio de existe un valor en el dominio de tal que satisface la restricción binaria entre y . Un problema es arcoconsistente si cada variable es arcoconsistente con todas las demás. ${\displaystyle x_{i}}$ ${\displaystyle x_{j}}$ ${\displaystyle a}$ ${\displaystyle x_{i}}$ ${\displaystyle b}$ ${\displaystyle x_{j}}$ ${\displaystyle (a,b)}$ ${\displaystyle x_{i}}$ ${\displaystyle x_{j}}$

Por ejemplo, considere la restricción donde las variables van del dominio 1 al 3. Como nunca puede ser 3, no hay arco desde 3 hasta un valor en , por lo que es seguro eliminarlo. Del mismo modo, nunca puede ser 1, por lo que no hay arco, por lo que se puede eliminar. ${\displaystyle x<y}$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle y}$

La consistencia de arco también se puede definir en relación con una restricción binaria específica: una restricción binaria es consistente con arco si cada valor de una variable tiene un valor de la segunda variable tal que satisface la restricción. Esta definición de consistencia de arco es similar a la anterior, pero se da de manera específica para una restricción. Esta diferencia es especialmente relevante para problemas no normalizados, donde la definición anterior consideraría todas las restricciones entre dos variables mientras que esta considera solo una específica.

Se aplica la coherencia de arco eliminando 1 como valor para x2. Como resultado, x3 ya no es coherente con x2 porque x3=2 no corresponde a un valor para x2.

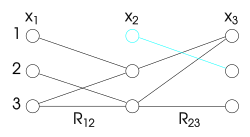
Si una variable no es coherente con otra, se puede lograr que lo sea eliminando algunos valores de su dominio. Esta es la forma de propagación de restricciones que impone la coherencia con otra variable: elimina, del dominio de la variable, todos los valores que no corresponden a un valor de la otra variable. Esta transformación mantiene las soluciones del problema, ya que los valores eliminados no son, de todos modos, una solución.

La propagación de restricciones puede hacer que todo el problema sea coherente al repetir esta eliminación para todos los pares de variables. Este proceso podría tener que considerar un par de variables determinado más de una vez. De hecho, eliminar valores del dominio de una variable puede hacer que otras variables ya no sean coherentes con ella. Por ejemplo, si es coherente con pero el algoritmo reduce el dominio de , la coherencia de con ya no se cumple y debe aplicarse nuevamente. ${\displaystyle x_{3}}$ ${\displaystyle x_{2}}$ ${\displaystyle x_{2}}$ ${\displaystyle x_{3}}$ ${\displaystyle x_{2}}$

Un algoritmo simplista recorrería los pares de variables, imponiendo la consistencia del arco, repitiendo el ciclo hasta que no cambie ningún dominio durante un ciclo completo. El algoritmo AC-3 mejora este algoritmo al ignorar las restricciones que no se han modificado desde que se analizaron por última vez. En particular, funciona sobre un conjunto de restricciones que inicialmente contiene todas las restricciones; en cada paso, toma una restricción y aplica la consistencia del arco; si esta operación puede haber producido una violación de la consistencia del arco sobre otra restricción, coloca esa restricción nuevamente en el conjunto de restricciones para analizar. De esta manera, una vez que se aplica la consistencia del arco sobre una restricción, esta restricción no se considera nuevamente a menos que se cambie el dominio de una de sus variables.

Consistencia de ruta (consistencia k)

x1 y x2 no son coherentes con x3. Se pueden hacer coherentes eliminando los valores azules de R12.

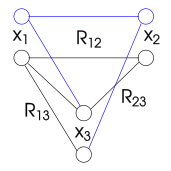
La consistencia de ruta es una propiedad similar a la consistencia de arco, pero considera pares de variables en lugar de solo una. Un par de variables es consistente en ruta con una tercera variable si cada evaluación consistente del par se puede extender a la otra variable de tal manera que se satisfacen todas las restricciones binarias . Formalmente, y son consistentes en ruta con si, para cada par de valores que satisface la restricción binaria entre y , existe un valor en el dominio de tal que y satisfacen la restricción entre y y entre y , respectivamente. ${\displaystyle x_{i}}$ ${\displaystyle x_{j}}$ ${\displaystyle x_{k}}$ ${\displaystyle (a,b)}$ ${\displaystyle x_{i}}$ ${\displaystyle x_{j}}$ ${\displaystyle c}$ ${\displaystyle x_{k}}$ ${\displaystyle (a,c)}$ ${\displaystyle (b,c)}$ ${\displaystyle x_{i}}$ ${\displaystyle x_{k}}$ ${\displaystyle x_{j}}$ ${\displaystyle x_{k}}$

La forma de propagación de restricciones que hace cumplir la consistencia de la ruta funciona eliminando alguna asignación satisfactoria de una restricción. De hecho, la consistencia de la ruta se puede hacer cumplir eliminando de una restricción binaria todas las evaluaciones que no se pueden extender a otra variable. En cuanto a la consistencia de arco, esta eliminación podría tener que considerar una restricción binaria más de una vez. En cuanto a la consistencia de arco, el problema resultante tiene las mismas soluciones que el original, ya que los valores eliminados no tienen solución.

Dos variables que no están en una restricción pueden considerarse relacionadas por una restricción virtual que permite cualquier par posible de valores, representados por los bordes azules en esta figura.

Al aplicar la coherencia de trayectoria de x1 y x2 con x3 se elimina la arista en la parte superior. Los valores de x1 y x2 ya no son libres, sino que están relacionados por una nueva restricción real.

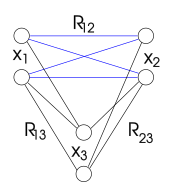
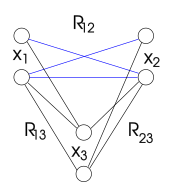
La forma de propagación de restricciones que impone la coherencia de las rutas puede introducir nuevas restricciones. Cuando dos variables no están relacionadas por una restricción binaria, están virtualmente relacionadas por la restricción que permite cualquier par de valores. Sin embargo, algún par de valores puede eliminarse por la propagación de restricciones. La restricción resultante ya no se satisface con todos los pares de valores. Por lo tanto, ya no es una restricción virtual y trivial.

El nombre "consistencia de ruta" deriva de la definición original, que implicaba un par de variables y una ruta entre ellas, en lugar de un par y una sola variable. Si bien las dos definiciones son diferentes para un solo par de variables, son equivalentes cuando se refieren al problema en su totalidad.

Generalizaciones

La consistencia de arcos y trayectorias se puede generalizar a restricciones no binarias utilizando tuplas de variables en lugar de una sola o un par. Una tupla de variables es -consistente con otra variable si cada evaluación consistente de las variables se puede extender con un valor de la otra variable mientras se preserva la consistencia. Esta definición se extiende a problemas completos de la manera obvia. La -consistencia fuerte es -consistencia para todos los . ${\displaystyle i-1}$ ${\displaystyle i}$ ${\displaystyle i-1}$ ${\displaystyle i}$ ${\displaystyle j}$ ${\displaystyle j\leq i}$

El caso particular de la 2-consistencia coincide con la consistencia de arco (en este artículo se supone que todos los problemas son consistentes con los nodos). Por otro lado, la 3-consistencia coincide con la consistencia de trayectoria solo si todas las restricciones son binarias, porque la consistencia de trayectoria no implica restricciones ternarias, mientras que la 3-consistencia sí.

Otra forma de generalizar la consistencia de arco es la consistencia hiperarco o consistencia arco generalizada , que requiere la extensibilidad de una sola variable para satisfacer una restricción. Es decir, una variable es hiperarco consistente con una restricción si cada valor de la variable puede extenderse a las otras variables de la restricción de tal manera que se satisfaga la restricción.

Coherencia y satisfacibilidad

Esta instancia es coherente con el arco y no contiene ningún dominio vacío, pero no tiene solución. Las líneas azules indican asignaciones forzadas por la opción x1=1.

La propagación de restricciones (que impone una forma de consistencia local) puede producir un dominio vacío o una restricción insatisfactoria . En este caso, el problema no tiene solución. Lo inverso no es cierto en general: una instancia inconsistente puede ser consistente con arcos o con trayectorias sin tener un dominio vacío o una restricción insatisfactoria.

De hecho, la consistencia local solo es relativa a la consistencia de grupos de variables. Por ejemplo, la consistencia de arco garantiza que cada evaluación consistente de una variable se pueda extender de manera consistente a otra variable. Sin embargo, cuando un único valor de una variable se extiende a otras dos variables, no hay garantía de que estos dos valores sean consistentes entre sí. Por ejemplo, pueden ser consistentes con y con , pero estas dos evaluaciones pueden no ser consistentes entre sí. ${\displaystyle x_{1}=1}$ ${\displaystyle x_{2}=1}$ ${\displaystyle x_{3}=1}$

Sin embargo, la propagación de restricciones se puede utilizar para demostrar la satisfacibilidad en algunos casos. Un conjunto de restricciones binarias que es coherente con un arco y no tiene un dominio vacío puede ser inconsistente solo si la red de restricciones contiene ciclos. De hecho, si las restricciones son binarias y forman un gráfico acíclico, los valores siempre se pueden propagar a través de las restricciones: para cada valor de una variable, todas las variables en una restricción con ella tienen un valor que satisface esa restricción. Como resultado, se puede encontrar una solución eligiendo iterativamente una variable no asignada y propagándola recursivamente a través de las restricciones. Este algoritmo nunca intenta asignar un valor a una variable que ya está asignada, ya que eso implicaría la existencia de ciclos en la red de restricciones.

Una condición similar se aplica a la coherencia de la trayectoria. Los casos especiales en los que se puede establecer la satisfacibilidad imponiendo la coherencia del arco y de la trayectoria son los siguientes.

1. la aplicación de la consistencia del arco establece la satisfacibilidad de problemas formados por restricciones binarias sin ciclos (un árbol de restricciones binarias);
2. la aplicación de la consistencia de la ruta establece la satisfacibilidad de las restricciones binarias (posiblemente con ciclos) con dominios binarios;
3. La aplicación de una fuerte consistencia establece la satisfacibilidad de los problemas que contienen variables. ${\displaystyle n}$ ${\displaystyle n}$

Casos especiales

Algunas definiciones o resultados sobre la consistencia relativa sólo son válidos en casos especiales.

Cuando los dominios están compuestos por números enteros , se puede definir la consistencia de límites. Esta forma de consistencia se basa en la consistencia de los valores extremos de los dominios, es decir, los valores mínimos y máximos que puede tomar una variable.

Cuando las restricciones son algebraicas o booleanas , la consistencia del arco es equivalente a agregar una nueva restricción o modificar sintácticamente una antigua, y esto se puede hacer componiendo las restricciones adecuadamente.

Restricciones especializadas

Algunos tipos de restricciones se utilizan con frecuencia. Por ejemplo, se suele utilizar la restricción de que algunas variables sean todas diferentes. Existen algoritmos especializados y eficientes para aplicar la coherencia de arcos en dichas restricciones.

La restricción que obliga a que una serie de variables sean diferentes suele escribirse como o . Esta restricción es equivalente a la desigualdad de todos los pares de variables diferentes, es decir, para cada . Cuando el dominio de una variable se reduce a un único valor, este valor se puede eliminar de todos los demás dominios mediante la propagación de restricciones al imponer la coherencia de arco. El uso de la restricción especializada permite explotar propiedades que no se cumplen para desigualdades binarias individuales . ${\displaystyle \mathop {\rm {alldifferent}} (x_{1},\ldots ,x_{n})}$alldifferent([X1,...,Xn]) ${\displaystyle x_{i}\not =x_{j}}$ ${\displaystyle i\not =j}$

Una primera propiedad es que el número total de elementos en los dominios de todas las variables debe ser al menos el número de variables. Más precisamente, después de que se aplica la consistencia de arco, el número de variables no asignadas no debe exceder el número de valores en la unión de sus dominios. De lo contrario, la restricción no puede satisfacerse. Esta condición se puede verificar fácilmente en una restricción en la alldifferentforma, pero no corresponde a la consistencia de arco de la red de desigualdades. Una segunda propiedad de la alldifferentrestricción simple es que la consistencia de hiperarco se puede verificar de manera eficiente utilizando un algoritmo de coincidencia bipartita . En particular, se construye un grafo con variables y valores como los dos conjuntos de nodos, y se ejecuta en él un algoritmo de coincidencia de grafos bipartitos especializado para verificar la existencia de dicha coincidencia. ^[1]

Un tipo diferente de restricción que se utiliza comúnmente es cumulativela que se introdujo para problemas de programación y colocación. Como ejemplo, cumulative([S1,...,Sm], [D1,...,Dm], [R1,...,Rm], L)se puede utilizar para formalizar la condición en la que hay mactividades, cada una con tiempo de inicio si, duración diy que utilizan una cantidad ride un recurso. La restricción establece que la cantidad total disponible de recursos es L. Existen técnicas especializadas de propagación de restricciones para restricciones acumulativas; se utilizan diferentes técnicas según qué dominios de variables ya se hayan reducido a un único valor.

Una tercera restricción especializada que se utiliza en la programación de lógica de restricciones es la element1. En la programación de lógica de restricciones, se permiten listas como valores de variables. Una restricción element(I, L, X)se satisface si Les una lista y Xes el I-ésimo elemento de esta lista. Existen reglas de propagación de restricciones especializadas para estas restricciones. A modo de ejemplo, si Ly se reducen a un dominio de un solo valor, se puede determinar Iun valor único para . De manera más general, se pueden inferir valores imposibles de a partir del dominio de y viceversa.XX ${\displaystyle I}$

Consistencia direccional

La consistencia direccional es la variante de la consistencia de arco, trayectoria y -consistencia diseñada para ser utilizada por un algoritmo que asigna valores a variables siguiendo un orden dado de variables. Son similares a sus contrapartes no direccionales, pero solo requieren que una asignación consistente a algunas variables pueda extenderse consistentemente a otra variable que sea mayor que ellas según el orden. ${\displaystyle i}$

Arco direccional y consistencia de trayectoria

Una instancia que es coherente en cuanto a la dirección según el orden x1 x2 x3 pero no lo es (no hay ninguna restricción entre x1 y x3; se omiten los bordes correspondientes). Cada valor de una variable de índice inferior corresponde a valores de variables de índice superior. Los signos de interrogación indican puntos en los que no se cumple la regla inversa.

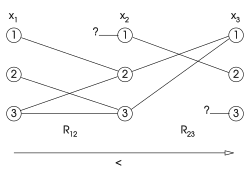
Si un algoritmo evalúa las variables en el orden , la consistencia solo es útil cuando garantiza que los valores de las variables de índice más bajo sean todos consistentes con los valores de las variables de índice más alto. ${\displaystyle x_{1},\ldots ,x_{n}}$

Al elegir un valor para una variable, se pueden ignorar los valores que son inconsistentes con todos los valores de una variable no asignada. De hecho, incluso si todos estos valores son consistentes con la evaluación parcial actual, el algoritmo no podrá encontrar posteriormente un valor consistente para la variable no asignada. Por otro lado, no es necesario aplicar la consistencia con las variables que ya se evaluaron: si el algoritmo elige un valor que es inconsistente con la evaluación parcial actual, la inconsistencia se detecta de todos modos.

Suponiendo que el orden de evaluación de las variables es , un problema de satisfacción de restricciones es coherente en cuanto a la dirección si cada variable es coherente en cuanto a la dirección con cualquier otra variable tal que . La coherencia en cuanto a la dirección es similar, pero dos variables tienen que ser coherentes en cuanto a la dirección solo si . La coherencia en cuanto a la dirección significa tanto coherencia en cuanto a la dirección como en cuanto a la dirección. Se pueden dar definiciones similares para las otras formas de coherencia. ${\displaystyle x_{1},\ldots ,x_{n}}$ ${\displaystyle x_{i}}$ ${\displaystyle x_{j}}$ ${\displaystyle i<j}$ ${\displaystyle x_{i},x_{j}}$ ${\displaystyle x_{z}}$ ${\displaystyle i,j<z}$

Propagación de restricciones para la consistencia del arco y la trayectoria

La propagación de restricciones que aplica la consistencia del arco direccional itera sobre las variables desde la última hasta la primera, y aplica en cada paso la consistencia del arco de cada variable de índice inferior con ella. Si el orden de las variables es , este algoritmo itera sobre las variables desde hasta ; para la variable , aplica la consistencia del arco de cada variable de índice inferior a con . ${\displaystyle x_{1},\ldots ,x_{n}}$ ${\displaystyle x_{n}}$ ${\displaystyle x_{1}}$ ${\displaystyle x_{j}}$ ${\displaystyle j}$ ${\displaystyle x_{j}}$

La coherencia de la ruta direccional y la coherencia fuerte de la ruta direccional se pueden aplicar mediante algoritmos similares al de la coherencia de arco. Procesan variables de a ; para cada variable se consideran dos variables con , y se aplica la coherencia de ruta de ellas con . No se requiere ninguna operación si el problema no contiene ninguna restricción en y o ninguna restricción entre y . Sin embargo, incluso si no hay ninguna restricción entre y , se supone que es trivial. Si la propagación de restricciones reduce su conjunto de asignaciones satisfactorias, crea efectivamente una nueva restricción no trivial. La propagación de restricciones que aplica una coherencia fuerte de la ruta direccional es similar, pero también aplica la coherencia de arco. ${\displaystyle x_{n}}$ ${\displaystyle x_{1}}$ ${\displaystyle x_{z}}$ ${\displaystyle x_{i},x_{j}}$ ${\displaystyle i,j<z}$ ${\displaystyle x_{z}}$ ${\displaystyle x_{i}}$ ${\displaystyle x_{z}}$ ${\displaystyle x_{j}}$ ${\displaystyle x_{z}}$ ${\displaystyle x_{i}}$ ${\displaystyle x_{j}}$

Consistencia direccional y satisfacibilidad

La consistencia direccional garantiza que las soluciones parciales que satisfacen una restricción se puedan extender de manera consistente a otra variable de índice más alto. Sin embargo, no garantiza que las extensiones a diferentes variables sean consistentes entre sí. Por ejemplo, una solución parcial se puede extender de manera consistente a la variable o a la variable , pero aun así estas dos extensiones no son consistentes entre sí. ${\displaystyle x_{i}}$ ${\displaystyle x_{j}}$

Hay dos casos en los que esto no sucede, y la consistencia direccional garantiza la satisfacibilidad si ningún dominio está vacío y ninguna restricción es insatisfacible.

El primer caso es el de un problema de restricción binaria con un ordenamiento de las variables que hace que el grafo ordenado de la restricción tenga un ancho de 1. Tal ordenamiento existe si y sólo si el grafo de restricciones es un árbol. Si este es el caso, el ancho del grafo limita el número máximo de nodos inferiores (según el ordenamiento) a los que se une un nodo. La consistencia del arco direccional garantiza que cada asignación consistente a una variable se pueda extender a nodos superiores, y el ancho 1 garantiza que un nodo no se una a más de un nodo inferior. Como resultado, una vez que se asigna la variable inferior, su valor se puede extender consistentemente a cada variable superior con la que se une. Esta extensión no puede conducir posteriormente a una inconsistencia. De hecho, ninguna otra variable inferior se une a esa variable superior, ya que el grafo tiene un ancho de 1.

Como resultado, si un problema de restricción tiene un ancho de 1 con respecto a un ordenamiento de sus variables (lo que implica que su gráfico correspondiente es un árbol) y el problema es direccionalmente consistente con respecto al mismo ordenamiento, se puede encontrar una solución (si hay alguna) asignando iterativamente las variables de acuerdo con el ordenamiento.

El segundo caso en el que la consistencia direccional garantiza la satisfacibilidad si ningún dominio está vacío y ninguna restricción es insatisfacible es el de los problemas de restricción binaria cuyo grafo tiene una anchura inducida de 2, utilizando una consistencia de trayectoria direccional fuerte. En efecto, esta forma de consistencia garantiza que cada asignación a una variable o a un par de variables se pueda extender a una variable superior, y la anchura 2 garantiza que esta variable no se una a otro par de variables inferiores.

La razón por la que se considera el ancho inducido en lugar del ancho es que hacer cumplir la consistencia de la ruta direccional puede agregar restricciones. De hecho, si dos variables no están en la misma restricción pero están en una restricción con una variable más alta, algunos pares de sus valores pueden violar la consistencia de la ruta. Eliminar dichos pares crea una nueva restricción. Como resultado, la propagación de restricciones puede producir un problema cuyo gráfico tiene más aristas que el original. Sin embargo, todas estas aristas están necesariamente en el gráfico inducido, ya que todas están entre dos padres del mismo nodo. El ancho 2 garantiza que cada evaluación parcial consistente se pueda extender a una solución, pero este ancho es relativo al gráfico generado. Como resultado, se requiere que el ancho inducido sea 2 para una fuerte consistencia de la ruta direccional para garantizar la existencia de soluciones.

i-Consistencia direccional

Las líneas azules indican que no existe ninguna restricción entre x3 y x4, por lo que se permite cualquier par de valores. En estas imágenes, la falta de aristas entre dos variables indica implícitamente la falta de una restricción. Este problema tiene una anchura de 2.

La consistencia direccional es la garantía de que cada asignación consistente a variables puede extenderse consistentemente a otra variable que esté en un nivel superior en el orden. La consistencia direccional fuerte se define de manera similar, pero se consideran todos los grupos de como máximo variables. Si un problema es consistente direccionalmente fuerte y tiene una anchura menor que y no tiene un dominio vacío o una restricción insatisfactoria, tiene soluciones. ${\displaystyle i}$ ${\displaystyle i-1}$ ${\displaystyle i}$ ${\displaystyle i-1}$ ${\displaystyle i}$ ${\displaystyle i}$

Cada problema puede hacerse fuertemente consistente direccionalmente, pero esta operación puede incrementar el ancho de sus gráficos correspondientes. El procedimiento de propagación de restricciones que hace cumplir la consistencia direccional es similar al utilizado para la consistencia de arco direccional y la consistencia de trayectoria. Las variables se consideran a su vez, desde la última hasta la primera según el orden. Para la variable , el algoritmo considera cada grupo de variables que tienen índice menor que y están en una restricción con . La consistencia de estas variables con se verifica y posiblemente se hace cumplir eliminando asignaciones satisfactorias de la restricción entre todas estas variables (si las hay, o creando una nueva en caso contrario). ${\displaystyle i}$ ${\displaystyle x_{k}}$ ${\displaystyle i-1}$ ${\displaystyle k}$ ${\displaystyle x_{k}}$ ${\displaystyle x_{k}}$ ${\displaystyle i}$

Al aplicar la coherencia a x5 se elimina la línea roja, lo que crea una nueva restricción no trivial entre x3 y x4. Como resultado, x4 tiene a x3 como nuevo padre, además de x1 y x2. Este cambio aumenta el ancho a 3.

Este procedimiento genera una instancia fuertemente consistente direccionalmente. Sin embargo, también puede agregar nuevas restricciones a la instancia. Como resultado, incluso si el ancho del problema original es , el ancho de la instancia resultante puede ser mayor. Si este es el caso, la fuerte consistencia direccional no implica satisfacibilidad incluso si ningún dominio está vacío y ninguna restricción es insatisfacible. ${\displaystyle i}$ ${\displaystyle i}$

Sin embargo, la propagación de restricciones solo agrega restricciones a las variables que son inferiores a la que está considerando actualmente. Como resultado, no se modifica ni se agrega ninguna restricción sobre una variable una vez que el algoritmo ha tratado con esta variable. En lugar de considerar un fijo , se puede modificar al número de padres de cada variable considerada (los padres de una variable son las variables de índice inferior a la variable y que están en una restricción con la variable). Esto corresponde a considerar todos los padres de una variable dada en cada paso. En otras palabras, para cada variable desde la última hasta la primera, todos sus padres se incluyen en una nueva restricción que limita sus valores a los que son consistentes con . Dado que este algoritmo puede verse como una modificación del anterior con un valor que se cambia al número de padres de cada nodo, se llama consistencia adaptativa . ${\displaystyle i}$ ${\displaystyle x_{i}}$ ${\displaystyle x_{i}}$ ${\displaystyle i}$

Este algoritmo aplica una consistencia direccional fuerte con un ancho igual al inducido del problema. La instancia resultante es satisfacible si y solo si ningún dominio o restricción se deja vacío. Si este es el caso, se puede encontrar fácilmente una solución al establecer iterativamente una variable no asignada en un valor arbitrario y propagar esta evaluación parcial a otras variables. Este algoritmo no siempre es de tiempo polinómico, ya que la cantidad de restricciones introducidas al aplicar una consistencia direccional fuerte puede producir un aumento exponencial del tamaño. Sin embargo, el problema se puede resolver en tiempo polinómico si la aplicación de una consistencia direccional fuerte no amplía la instancia de manera superpolinómica . Como resultado, si una instancia tiene un ancho inducido limitado por una constante, se puede resolver en tiempo polinómico. ${\displaystyle i}$ ${\displaystyle i}$

Eliminación de cubos

La eliminación de contenedores es un algoritmo de satisfacibilidad. Se puede definir como una reformulación de la consistencia adaptativa. Sus definiciones utilizan contenedores, que son contenedores para restricciones, y cada variable tiene un contenedor asociado. Una restricción siempre pertenece al contenedor de su variable más alta.

El algoritmo de eliminación de cubos procede de la variable más alta a la más baja, por turno. En cada paso, se consideran las restricciones en los cubos de esta variable. Por definición, estas restricciones solo involucran variables que son menores que . El algoritmo modifica la restricción entre estas variables menores (si las hay, de lo contrario crea una nueva). En particular, hace que sus valores sean extensibles a de manera consistente con las restricciones en el cubo de . Esta nueva restricción, si la hay, se coloca luego en el cubo apropiado. Dado que esta restricción solo involucra variables que son menores que , se agrega a un cubo de una variable que es menor que . ${\displaystyle x_{i}}$ ${\displaystyle x_{i}}$ ${\displaystyle x_{i}}$ ${\displaystyle x_{i}}$ ${\displaystyle x_{i}}$ ${\displaystyle x_{i}}$

Este algoritmo es equivalente a aplicar la coherencia adaptativa. Dado que ambos aplican la coherencia de una variable con todos sus padres y dado que no se agrega ninguna restricción nueva después de considerar una variable, el resultado es una instancia que se puede resolver sin retroceder .

Dado que el gráfico de la instancia que producen es un subgráfico del gráfico inducido, si el ancho inducido está limitado por una constante, la instancia generada tiene un tamaño polinómico en relación con el tamaño de la instancia original. Como resultado, si el ancho inducido de una instancia está limitado por una constante, su resolución se puede realizar en tiempo polinómico mediante los dos algoritmos.

Consistencia relacional

Si bien las definiciones anteriores de consistencia se refieren a la consistencia de las asignaciones, la consistencia relacional implica únicamente la satisfacción de una restricción o un conjunto de restricciones dadas. Más precisamente, la consistencia relacional implica que cada asignación parcial consistente puede extenderse de tal manera que se satisface una restricción o un conjunto de restricciones dadas. Formalmente, una restricción sobre las variables es consistente con una de sus variables si cada asignación consistente que pueda extenderse de tal manera se satisface. La diferencia entre la consistencia "regular" y la consistencia relacional es que esta última solo requiere que la asignación extendida satisfaga una restricción dada, mientras que la primera requiere que satisfaga todas las restricciones relevantes. ${\displaystyle C}$ ${\displaystyle X}$ ${\displaystyle x}$ ${\displaystyle X\backslash \{x\}}$ ${\displaystyle x}$ ${\displaystyle C}$ ${\displaystyle i}$

(Regular) i-Consistencia: si una evaluación es consistente, puede extenderse a otra variable de tal manera que se satisfagan todas las restricciones relevantes.

Consistencia de arco relacional: si una evaluación sobre las variables de una restricción es consistente, siempre se puede extender a esa variable de tal manera que se satisfaga la restricción . Los bordes cian representan restricciones que no necesitan ser satisfechas por la extensión.

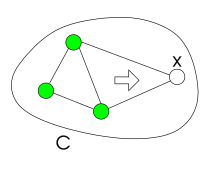
Esta definición se puede extender a más de una restricción y más de una variable. En particular, la consistencia de ruta relacional es similar a la consistencia de arco relacional, pero se utilizan dos restricciones en lugar de una. Dos restricciones son consistentes con una variable si cada asignación consistente a todas sus variables excepto la considerada se puede extender de tal manera que se cumplan las dos restricciones.

Para más de dos restricciones, se define la consistencia relacional. La consistencia relacional implica un conjunto de restricciones y una variable que está en el ámbito de todas estas restricciones. En particular, estas restricciones son consistentes relacionalmente con la variable si cada asignación consistente a todas las demás variables que están en sus ámbitos se puede extender a la variable de tal manera que se satisfacen estas restricciones. Un problema es consistente relacionalmente si cada conjunto de restricciones es consistente relacionalmente con cada variable que está en todos sus ámbitos. La consistencia relacional fuerte se define como se indicó anteriormente: es la propiedad de ser consistente relacionalmente para cada . ${\displaystyle m}$ ${\displaystyle m}$ ${\displaystyle m}$ ${\displaystyle m}$ ${\displaystyle m}$ ${\displaystyle m}$ ${\displaystyle m}$ ${\displaystyle m}$ ${\displaystyle m}$ ${\displaystyle k}$ ${\displaystyle k<m}$

La consistencia relacional también se puede definir para más variables, en lugar de una. Un conjunto de restricciones es consistente con las relaciones si cada asignación consistente a un subconjunto de sus variables se puede extender a una evaluación de todas las variables que satisface todas las restricciones. Esta definición no extiende exactamente lo anterior porque las variables a las que se supone que se pueden extender las evaluaciones no están necesariamente en todos los ámbitos de las restricciones involucradas. ${\displaystyle m}$ ${\displaystyle (i,m)}$ ${\displaystyle i}$

Si se proporciona un orden de las variables, la coherencia relacional se puede restringir a los casos en que las variables que se evalúan deben poder extenderse para seguir a las demás variables en el orden. Esta condición modificada se denomina coherencia relacional direccional.

Consistencia relacional y satisfacibilidad

Un problema de satisfacción de restricciones puede ser relacionalmente consistente, no tener un dominio vacío ni una restricción insatisfacible y, aun así, ser insatisfacible. Sin embargo, existen algunos casos en los que esto no es posible.

El primer caso es el de un problema de coherencia relacional fuerte, en el que los dominios contienen como máximo elementos. En este caso, una evaluación consistente de variables siempre se puede extender a una única variable. Si es una evaluación de este tipo y es la variable, solo hay valores posibles que la variable puede tomar. Si todos esos valores son inconsistentes con la evaluación, hay restricciones (no necesariamente únicas) que son violadas por la evaluación y uno de sus valores posibles. Como resultado, la evaluación no se puede extender para satisfacer todas estas restricciones -o menos, violando la condición de coherencia relacional fuerte. ${\displaystyle m}$ ${\displaystyle m}$ ${\displaystyle k}$ ${\displaystyle x_{1}=a_{1},\ldots ,x_{k}=a_{k}}$ ${\displaystyle x_{k+1}}$ ${\displaystyle m}$ ${\displaystyle m}$ ${\displaystyle m}$ ${\displaystyle m}$

El segundo caso se relaciona con una medida de las restricciones, en lugar de los dominios. Una restricción es estricta si cada evaluación de todas sus variables, excepto una, puede extenderse para satisfacer la restricción ya sea por todos los valores posibles de la otra variable o por la mayoría de sus valores. El problema de tener restricciones estrictas es que se pueden satisfacer si y solo si son fuertemente consistentes desde el punto de vista relacional. ${\displaystyle m}$ ${\displaystyle m}$ ${\displaystyle m}$ ${\displaystyle m+1}$

Una matriz convexa por filas: los 1 en cada fila son contiguos (no hay 0 entre ellos).

El tercer caso es el de las restricciones binarias que se pueden representar mediante matrices convexas por filas. Una restricción binaria se puede representar mediante una matriz bidimensional , donde es 0 o 1 dependiendo de si el valor -ésimo del dominio de y el valor -ésimo del dominio de satisfacen la restricción. Una fila de esta matriz es convexa si los 1 que contiene son consecutivos (formalmente, si dos elementos son 1, todos los elementos intermedios también lo son). Una matriz es convexa por filas si todas sus filas son convexas. ${\displaystyle M}$ ${\displaystyle M_{ij}}$ ${\displaystyle i}$ ${\displaystyle x_{i}}$ ${\displaystyle j}$ ${\displaystyle x_{j}}$

Cada matriz representa la restricción entre x _i y x _{k +1} . Si a ₁ ... a _k son valores para x ₁ ... x _k , las filas de a ₁ ... a _k en cada matriz indican los valores permitidos para x _{k +1} . La convexidad de filas y la fuerte consistencia de la ruta relacional implican la existencia de un valor consistente a _{k +1} para x _{k +1} .

La condición que hace que la consistencia de caminos relacionales fuertes sea equivalente a la satisfacibilidad es la de los problemas de satisfacción de restricciones para los cuales existe un orden de las variables que hace que todas las restricciones sean representadas por matrices convexas por filas. Este resultado se basa en el hecho de que un conjunto de filas convexas que tienen un elemento común por pares también tienen un elemento común globalmente. Considerando una evaluación sobre variables, los valores permitidos para la -ésima variable se dan seleccionando algunas filas de algunas restricciones. En particular, para cada variable entre las unas, la fila relativa a su valor en la matriz que representa la restricción que la relaciona con la una representa los valores permitidos de esta última. Dado que estas filas son convexas y tienen un elemento común por pares debido a la consistencia de caminos, también tienen un elemento común compartido, que representa un valor de la última variable que es consistente con las otras. ${\displaystyle k}$ ${\displaystyle k+1}$ ${\displaystyle k}$ ${\displaystyle k+1}$

Usos de la consistencia local

Todas las formas de consistencia local pueden ser impuestas por la propagación de restricciones, que puede reducir los dominios de las variables y los conjuntos de asignaciones que satisfacen una restricción y puede introducir nuevas restricciones. Siempre que la propagación de restricciones produzca un dominio vacío o una restricción insatisfacible, el problema original es insatisfacible. Por lo tanto, todas las formas de consistencia local pueden usarse como aproximaciones de satisfacibilidad. Más precisamente, pueden usarse como algoritmos de insatisfacibilidad incompletos, ya que pueden probar que un problema es insatisfacible, pero en general son incapaces de probar que un problema es satisfacible. Dichos algoritmos aproximados pueden ser utilizados por algoritmos de búsqueda ( backtracking , backjumping , búsqueda local , etc.) como heurísticas para decir si una solución parcial puede extenderse para satisfacer todas las restricciones sin analizarla más.

Incluso si la propagación de restricciones no produce un dominio vacío o una restricción insatisfactoria, puede reducir los dominios o fortalecer las restricciones. Si este es el caso, se reduce el espacio de búsqueda del problema, lo que reduce la cantidad de búsqueda necesaria para resolverlo.

La consistencia local demuestra la satisfacibilidad en algunos casos restringidos (ver Complejidad de la satisfacción de restricciones#Restricciones ). Este es el caso de algunos tipos especiales de problemas y/o de algunos tipos de consistencia local. Por ejemplo, imponer la consistencia de arco en problemas acíclicos binarios permite determinar si el problema es satisfacible. Imponer una fuerte consistencia direccional permite determinar la satisfacibilidad de problemas que tienen un ancho inducido de acuerdo con el mismo orden. La consistencia direccional adaptativa permite determinar la satisfacibilidad de un problema arbitrario. ${\displaystyle i}$ ${\displaystyle i-1}$

Véase también

• Propagación de unidades
• Programación de restricciones
• Programación lógica de restricciones
• Mirar hacia adelante (retroceder)

Enlaces externos

• Propagación de restricciones: tesis de Guido Tack que ofrece un buen panorama de la teoría y los problemas de implementación

Referencias

1. Régin, Jean-Charles (julio de 1994). "Un algoritmo de filtrado para restricciones de diferencia en CSP" (PDF) . Actas de la Conferencia AAAI . Consultado el 16 de diciembre de 2022 .

• Lecoutre, Christophe (2009). Redes de restricciones: técnicas y algoritmos. ISTE/Wiley. Número de publicación:  978-1-84821-106-3
• Dechter, Rina (2003). Procesamiento de restricciones. Morgan Kaufmann. ISBN  1-55860-890-7
• Apt, Krzysztof (2003). Principios de programación con restricciones . Cambridge University Press. ISBN  0-521-82583-0
• Marriott, Kim; Peter J. Stuckey (1998). Programación con restricciones: una introducción . MIT Press. ISBN  0-262-13341-5