
En matemáticas discretas , la rotación de árboles es una operación en un árbol binario que cambia la estructura sin interferir con el orden de los elementos. Una rotación de árboles mueve un nodo hacia arriba en el árbol y un nodo hacia abajo. Se utiliza para cambiar la forma del árbol y, en particular, para disminuir su altura moviendo subárboles más pequeños hacia abajo y subárboles más grandes hacia arriba, lo que da como resultado un mejor rendimiento de muchas operaciones de árboles.
Existe una inconsistencia en las diferentes descripciones en cuanto a la definición de la dirección de las rotaciones . Algunos dicen que la dirección de rotación refleja la dirección en la que se mueve un nodo al rotar (un hijo izquierdo que rota hacia la ubicación de su padre es una rotación hacia la derecha), mientras que otros dicen que la dirección de rotación refleja qué subárbol está rotando (un subárbol izquierdo que rota hacia la ubicación de su padre es una rotación hacia la izquierda, lo opuesto a lo anterior). Este artículo adopta el enfoque del movimiento direccional del nodo rotatorio.

La operación de rotación a la derecha que se muestra en la imagen adyacente se realiza con Q como raíz y, por lo tanto, es una rotación a la derecha o con raíz en Q. Esta operación da como resultado una rotación del árbol en el sentido de las agujas del reloj. La operación inversa es la rotación a la izquierda, que da como resultado un movimiento en el sentido contrario a las agujas del reloj (la rotación a la izquierda que se muestra arriba tiene su raíz en P ). La clave para entender cómo funciona una rotación es comprender sus restricciones. En particular, el orden de las hojas del árbol (cuando se leen de izquierda a derecha, por ejemplo) no puede cambiar (otra forma de pensarlo es que el orden en que se visitarían las hojas en un recorrido en orden debe ser el mismo después de la operación que antes). Otra restricción es la propiedad principal de un árbol de búsqueda binario, es decir, que todos los nodos en el subárbol derecho son mayores que el padre y todos los nodos en el subárbol izquierdo son menores que el padre . Observe que el hijo derecho de un hijo izquierdo de la raíz de un subárbol (por ejemplo, el nodo B en el diagrama del árbol con raíz en Q) puede convertirse en el hijo izquierdo de la raíz, que a su vez se convierte en el hijo derecho de la "nueva" raíz en el subárbol rotado, sin violar ninguna de esas restricciones. Como se ve en el diagrama, el orden de las hojas no cambia. La operación opuesta también conserva el orden y es el segundo tipo de rotación.
Suponiendo que se trata de un árbol de búsqueda binario , como se indicó anteriormente, los elementos deben interpretarse como variables que se pueden comparar entre sí. Los caracteres alfabéticos de la izquierda se utilizan como marcadores de posición para estas variables. En la animación de la derecha, los caracteres alfabéticos en mayúscula se utilizan como marcadores de posición de variables, mientras que las letras griegas en minúscula son marcadores de posición para un conjunto completo de variables. Los círculos representan nodos individuales y los triángulos representan subárboles. Cada subárbol puede estar vacío, constar de un solo nodo o constar de cualquier número de nodos.
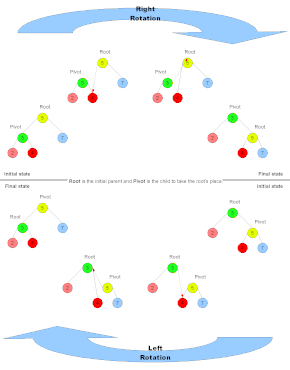
Cuando se rota un subárbol, el lado del subárbol sobre el que se rota aumenta su altura en un nodo, mientras que el otro subárbol la disminuye. Esto hace que las rotaciones de árboles sean útiles para reequilibrar un árbol.
Considere la terminología de raíz para el nodo padre de los subárboles que se rotarán, pivote para el nodo que se convertirá en el nuevo nodo padre, RS para el lado de la rotación y OS para el lado opuesto de la rotación. Para la raíz Q en el diagrama anterior, RS es C y OS es P. Usando estos términos, el pseudocódigo para la rotación es:
deje que Pivot = Root.OSRaíz.OS = Pivot.RSPivot.RS = RaízRaíz = Pivote
Esta es una operación de tiempo constante.
El programador también debe asegurarse de que el padre de la raíz apunte al pivote después de la rotación. Además, el programador debe tener en cuenta que esta operación puede generar una nueva raíz para todo el árbol y debe tener cuidado de actualizar los punteros en consecuencia.
La rotación del árbol hace que el recorrido en orden del árbol binario sea invariante . Esto implica que el orden de los elementos no se ve afectado cuando se realiza una rotación en cualquier parte del árbol. A continuación, se muestran los recorridos en orden de los árboles que se muestran arriba:
Árbol izquierdo: ((A, P, B), Q, C) Árbol derecho: (A, P, (B, Q, C))
Calcular uno a partir del otro es muy sencillo. El siguiente es un ejemplo de código Python que realiza ese cálculo:
def right_rotation ( treenode ): """Rotar el árbol especificado hacia la derecha.""" left , Q , C = treenode A , P , B = left return ( A , P , ( B , Q , C )) Otra forma de verlo es:
Rotación derecha del nodo Q:
Sea P el hijo izquierdo de Q.Establezca el hijo izquierdo de Q como el hijo derecho de P.[Establecer como padre del hijo derecho de P Q]Establezca el hijo derecho de P como Q.[Establecer el padre de Q en P]
Rotación hacia la izquierda del nodo P:
Sea Q el hijo derecho de P.Establezca el hijo derecho de P como el hijo izquierdo de Q.[Establecer como padre del hijo izquierdo de Q el valor P]Establezca el hijo izquierdo de Q como P.[Establecer el padre de P en Q]
Todas las demás conexiones se dejan como están.
También existen rotaciones dobles , que son combinaciones de rotaciones a la izquierda y a la derecha. Una doble rotación a la izquierda en X puede definirse como una rotación a la derecha en el hijo derecho de X seguida de una rotación a la izquierda en X; de manera similar, una doble rotación a la derecha en X puede definirse como una rotación a la izquierda en el hijo izquierdo de X seguida de una rotación a la derecha en X.
Las rotaciones de árboles se utilizan en varias estructuras de datos de árboles, como árboles AVL , árboles rojo-negros , árboles WAVL , árboles splay y treaps . Requieren solo tiempo constante porque son transformaciones locales : solo operan en 5 nodos y no necesitan examinar el resto del árbol.

Un árbol se puede reequilibrar mediante rotaciones. Después de una rotación, el lado de la rotación aumenta su altura en 1, mientras que el lado opuesto a la rotación disminuye su altura de manera similar. Por lo tanto, se pueden aplicar rotaciones estratégicamente a los nodos cuyos hijos izquierdo y derecho difieren en altura en más de 1. Los árboles de búsqueda binaria autoequilibrados aplican esta operación automáticamente. Un tipo de árbol que utiliza esta técnica de reequilibrio es el árbol AVL .
La distancia de rotación entre dos árboles binarios cualesquiera con el mismo número de nodos es el número mínimo de rotaciones necesarias para transformar uno en el otro. Con esta distancia, el conjunto de árboles binarios de n nodos se convierte en un espacio métrico : la distancia es simétrica, positiva cuando se dan dos árboles diferentes y satisface la desigualdad triangular .
Es un problema abierto si existe un algoritmo de tiempo polinomial para calcular la distancia de rotación, aunque varias variantes del problema de la distancia de rotación admiten algoritmos de tiempo polinomial. [1] [2] [3]
Daniel Sleator , Robert Tarjan y William Thurston demostraron que la distancia de rotación entre dos árboles de n nodos (para n ≥ 11) es como máximo 2 n − 6, y que algunos pares de árboles están tan separados tan pronto como n es suficientemente grande. [4] Lionel Pournin demostró que, de hecho, tales pares existen siempre que n ≥ 11. [5]