En redes informáticas , las redes de hipercubos son un tipo de topología de red que se utiliza para conectar y enrutar datos entre varias unidades de procesamiento o computadoras. Las redes de hipercubos constan de 2 m nodos , que forman los vértices de los cuadrados para crear una conexión entre redes . Un hipercubo es básicamente una red en malla multidimensional con dos nodos en cada dimensión. Debido a la similitud, dichas topologías suelen agruparse en una familia de topologías en malla k -aria d -dimensional, donde d representa el número de dimensiones y k representa el número de nodos en cada dimensión. [1]
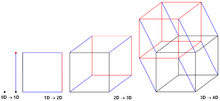
La red de interconexión de hipercubos se forma conectando N nodos que pueden expresarse como una potencia de 2. Esto significa que si la red tiene N nodos, se puede expresar como:
donde m es el número de bits que se requieren para etiquetar los nodos en la red. Entonces, si hay 4 nodos en la red, se necesitan 2 bits para representar todos los nodos en la red . La red se construye conectando los nodos que solo difieren en un bit en su representación binaria . Esto se conoce comúnmente como etiquetado binario. Una interred de hipercubos 3D sería un cubo con 8 nodos y 12 aristas . Una red de hipercubos 4D se puede crear duplicando dos redes 3D y agregando un bit más significativo. El nuevo bit agregado debe ser '0' para un hipercubo 3D y '1' para el otro hipercubo 3D. Las esquinas de los respectivos MSB cambiados de un bit se conectan para crear la red de hipercubos superior. Este método se puede utilizar para construir cualquier hipercubo representado por m bits con un hipercubo representado por (m-1) bits. [2]
El método de enrutamiento para una red de hipercubos se denomina enrutamiento E-Cube. La distancia entre dos nodos de la red se puede obtener mediante el peso de Hamming (número de unos en) la operación XOR entre sus respectivas etiquetas binarias.
La distancia entre el Nodo 1 (representado como '01') y el Nodo 2 (representado como '10') en la red viene dada por:
El enrutamiento E-Cube es un método de enrutamiento estático que emplea el algoritmo de enrutamiento XY . Esto se conoce comúnmente como modelo de enrutamiento determinista de dimensión ordenada . El enrutamiento E-Cube funciona recorriendo la red en la dimensión k , donde k es el bit distinto de cero menos significativo en el resultado del cálculo de la distancia.
Por ejemplo, supongamos que la etiqueta del remitente es '00' y la del receptor es '11'. Por lo tanto, la distancia entre ellos es 11 y el bit menos significativo distinto de cero es el bit LSB . El algoritmo de enrutamiento XY determina qué camino tomar para un '0' o un '1'. [3]
Se utilizan diferentes medidas de rendimiento para evaluar la eficiencia de una conexión de red de hipercubo frente a varias otras topologías de red. [ vago ]
Esto define la cantidad de nodos inmediatamente adyacentes a un nodo en particular. Estos nodos deben ser vecinos inmediatos. En el caso de un hipercubo, el grado es m.
Esto define el número máximo de nodos por los que debe pasar un mensaje en su camino desde el origen hasta el destino. Básicamente, esto nos da el retraso en la transmisión de un mensaje a través de una red. En el caso de un hipercubo, el diámetro es m.
La distancia entre dos nodos se define por el número de saltos en la ruta más corta entre dos nodos en particular. Se da por la fórmula:
En el caso de los hipercubos, la distancia promedio se expresa en m/2.
Este es el número mínimo de cables que debes cortar para dividir la red en dos mitades iguales. Se da como 2 m-1 para los hipercubos. [1]