Teoría de colisiones

Principio de química

La velocidad de reacción tiende a aumentar con la concentración , fenómeno explicado por la teoría de colisiones.

La teoría de colisiones es un principio de la química que se utiliza para predecir las velocidades de las reacciones químicas . Establece que cuando las partículas adecuadas del reactivo chocan entre sí con la orientación correcta, solo una cierta cantidad de colisiones dan como resultado un cambio perceptible o notable; estos cambios exitosos se denominan colisiones exitosas. Las colisiones exitosas deben tener suficiente energía, también conocida como energía de activación , en el momento del impacto para romper los enlaces preexistentes y formar todos los enlaces nuevos. Esto da como resultado los productos de la reacción. La energía de activación a menudo se predice utilizando la teoría del estado de transición . Aumentar la concentración del reactivo produce más colisiones y, por lo tanto, colisiones más exitosas. Aumentar la temperatura aumenta la energía cinética promedio de las moléculas en una solución, lo que aumenta el número de colisiones que tienen suficiente energía. La teoría de colisiones fue propuesta de forma independiente por Max Trautz en 1916 ^[1] y William Lewis en 1918. ^{[2] [3]}

Cuando interviene un catalizador en la colisión entre las moléculas reactivas, se requiere menos energía para que se produzca el cambio químico y, por lo tanto, más colisiones tienen energía suficiente para que se produzca la reacción. Por lo tanto, la velocidad de reacción aumenta.

La teoría de colisiones está estrechamente relacionada con la cinética química .

La teoría de colisiones se desarrolló inicialmente para el sistema de reacción de gases sin dilución. Pero la mayoría de las reacciones involucran soluciones, por ejemplo, las reacciones de gases en un gas inerte portador y casi todas las reacciones en soluciones. La frecuencia de colisión de las moléculas de soluto en estas soluciones ahora está controlada por la difusión o el movimiento browniano de moléculas individuales. El flujo de las moléculas difusivas sigue las leyes de difusión de Fick . Para las partículas en una solución, un modelo de ejemplo para calcular la frecuencia de colisión y la tasa de coagulación asociada es la ecuación de coagulación de Smoluchowski propuesta por Marian Smoluchowski en una publicación seminal de 1916. ^[4] En este modelo, el flujo de Fick en el límite de tiempo infinito se utiliza para imitar la velocidad de las partículas de la teoría de colisiones. Jixin Chen propuso una solución de tiempo finito para el flujo de difusión en 2022 que cambia significativamente la frecuencia de colisión estimada de dos partículas en una solución. ^[5]

Ecuaciones de velocidad

La velocidad de una reacción bimolecular en fase gaseosa, A + B → producto, predicha por la teoría de colisiones es ^[6]

${\displaystyle r(T)=kn_{\text{A}}n_{\text{B}}=Z\rho \exp \left({\frac {-E_{\text{a}}}{RT}}\right)}$

dónde:

• k es la constante de velocidad en unidades de (número de moléculas) ⁻¹ ⋅s ⁻¹ ⋅m ³ .
• n _A es la densidad numérica de A en el gas en unidades de m ⁻³ .
• n _B es la densidad numérica de B en el gas en unidades de m ⁻³ . Por ejemplo, para una mezcla de gases con una concentración de gas A de 0,1 mol⋅L ⁻¹ y una concentración de B de 0,2 mol⋅L ⁻¹ , la densidad numérica de A es 0,1×6,02×10 ²³ ÷10 ⁻³ = 6,02×10 ²⁵ m ⁻³ , la densidad numérica de B es 0,2×6,02×10 ²³ ÷10 ⁻³ = 1,2×10 ²⁶ m ⁻³
• Z es la frecuencia de colisión en unidades de m ⁻³ ⋅s ⁻¹ .
• ${\displaystyle \rho }$es el factor estérico . ^[7]
• E _a es la energía de activación de la reacción, en unidades de J⋅mol ⁻¹ .
• T es la temperatura en unidades de K.
• R es la constante del gas en unidades de J mol ⁻¹ K ⁻¹ .

La unidad de r ( T ) se puede convertir a mol⋅L ⁻¹ ⋅s ⁻¹ , después de dividir por (1000× N _A ), donde N _A es la constante de Avogadro .

Para una reacción entre A y B, la frecuencia de colisión calculada con el modelo de esfera dura con la unidad de número de colisiones por m ³ por segundo es:

${\displaystyle Z=n_{\text{A}}n_{\text{B}}\sigma _{\text{AB}}{\sqrt {\frac {8k_{\text{B}}T}{\pi \mu _{\text{AB}}}}}=10^{6}N_{A}^{2}{\text{[A][B]}}\sigma _{\text{AB}}{\sqrt {\frac {8k_{\text{B}}T}{\pi \mu _{\text{AB}}}}}}$

dónde:

• n _A es la densidad numérica de A en el gas en unidades de m ⁻³ .
• n _B es la densidad numérica de B en el gas en unidades de m ⁻³ . Por ejemplo, para una mezcla de gases con una concentración de gas A de 0,1 mol⋅L ⁻¹ y una concentración de B de 0,2 mol⋅L ⁻¹ , la densidad numérica de A es 0,1×6,02×10 ²³ ÷10 ⁻³ = 6,02×10 ²⁵ m ⁻³ , la densidad numérica de B es 0,2×6,02×10 ²³ ÷10 ⁻³ = 1,2×10 ²⁶ m ⁻³ .
• σ _AB es la sección transversal de reacción (unidad m ² ), el área cuando dos moléculas chocan entre sí, simplificada a , donde r _{A es} el radio de A y r _B es el radio de B en la unidad m. ${\displaystyle \sigma _{\text{AB}}=\pi (r_{\text{A}}+r_{\text{B}})^{2}}$
• k _B es la unidad de la constante de Boltzmann J⋅K ⁻¹ .
• T es la temperatura absoluta (unidad K).
• μ _AB es la masa reducida de los reactivos A y B, (unidad kg). ${\displaystyle \mu _{\text{AB}}={\frac {{m_{\text{A}}}{m_{\text{B}}}}{{m_{\text{A}}}+{m_{\text{B}}}}}}$
• N _A es la constante de Avogadro .
• [A] es la concentración molar de A en la unidad mol⋅L ⁻¹ .
• [B] es la concentración molar de B en la unidad mol⋅L ⁻¹ .
• Z se puede convertir a colisión de moles por litro por segundo dividiéndolo por 1000 N _A .

Si todas las unidades relacionadas con la dimensión se convierten a dm, es decir, mol⋅dm ⁻³ para [A] y [B], dm ² para σ _AB , dm ² ⋅kg⋅s ⁻² ⋅K ⁻¹ para la constante de Boltzmann , entonces

${\displaystyle Z=N_{\text{A}}\sigma _{\text{AB}}{\sqrt {\frac {8k_{\text{B}}T}{\pi \mu _{\text{AB}}}}}[{\text{A}}][{\text{B}}]=k[A][B]}$

unidad mol⋅dm ⁻³ ⋅s ⁻¹ .

Perspectivas cuantitativas

Derivación

Consideremos la reacción elemental bimolecular:

A + B → C

En la teoría de colisiones se considera que dos partículas A y B colisionarán si sus núcleos se acercan más de una cierta distancia. El área alrededor de una molécula A en la que puede colisionar con una molécula B que se aproxima se llama sección transversal (σ _AB ) de la reacción y es, en términos simplificados, el área correspondiente a un círculo cuyo radio ( ) es la suma de los radios de ambas moléculas reaccionantes, que se supone que son esféricas. Por lo tanto, una molécula en movimiento barrerá un volumen por segundo a medida que se mueve, donde es la velocidad promedio de la partícula. (Esto representa únicamente la noción clásica de una colisión de bolas sólidas. Como las moléculas son sistemas mecánico-cuánticos de muchas partículas de electrones y núcleos basados ​​en las interacciones de Coulomb y de intercambio, generalmente no obedecen a la simetría rotacional ni tienen un potencial de caja. Por lo tanto, de manera más general, la sección transversal se define como la probabilidad de reacción de un rayo de partículas A por densidad de área de objetivos B, lo que hace que la definición sea independiente de la naturaleza de la interacción entre A y B. En consecuencia, el radio está relacionado con la escala de longitud de su potencial de interacción). ${\displaystyle r_{AB}}$ ${\displaystyle \pi r_{AB}^{2}c_{A}}$ ${\displaystyle c_{A}}$ ${\displaystyle r_{AB}}$

De la teoría cinética se sabe que una molécula de A tiene una velocidad media (distinta de la velocidad cuadrática media ) de , donde es la constante de Boltzmann y es la masa de la molécula. ${\displaystyle c_{A}={\sqrt {\frac {8k_{\text{B}}T}{\pi m_{A}}}}}$ ${\displaystyle k_{\text{B}}}$ ${\displaystyle m_{A}}$

La solución del problema de los dos cuerpos establece que dos cuerpos móviles diferentes pueden considerarse como un solo cuerpo que tiene la masa reducida de ambos y se mueve con la velocidad del centro de masas , por lo que, en este sistema se debe utilizar en lugar de . Por lo tanto, para una molécula A dada, viaja antes de chocar con una molécula B si todo B está fijo sin movimiento, donde es la distancia recorrida media. Como B también se mueve, la velocidad relativa se puede calcular utilizando la masa reducida de A y B. ${\displaystyle \mu _{AB}}$ ${\displaystyle m_{A}}$ ${\displaystyle t=l/c_{A}=1/(n_{B}\sigma _{AB}c_{A})}$ ${\displaystyle l}$

Por lo tanto, la frecuencia total de colisión , ^[8] de todas las moléculas A, con todas las moléculas B, es

${\displaystyle Z=n_{\text{A}}n_{\text{B}}\sigma _{AB}{\sqrt {\frac {8k_{\text{B}}T}{\pi \mu _{AB}}}}=10^{6}N_{A}^{2}[A][B]\sigma _{AB}{\sqrt {\frac {8k_{\text{B}}T}{\pi \mu _{AB}}}}=z[A][B],}$

De la distribución de Maxwell-Boltzmann se puede deducir que la fracción de colisiones con mayor energía que la energía de activación es . Por lo tanto, la velocidad de una reacción bimolecular para gases ideales será ${\displaystyle e^{\frac {-E_{\text{a}}}{RT}}}$

${\displaystyle r=z\rho [A][B]\exp \left({\frac {-E_{\text{a}}}{RT}}\right),}$en unidad de número de reacciones moleculares s ⁻¹ ⋅m ⁻³ ,

dónde:

• Z es la frecuencia de colisión con unidad s ⁻¹ ⋅m ⁻³ . z es Z sin [A][B].
• ${\displaystyle \rho }$es el factor estérico , que se discutirá en detalle en la siguiente sección,
• E _a es la energía de activación (por mol) de la reacción en la unidad J/mol,
• T es la temperatura absoluta en unidad K,
• R es la constante del gas en unidades J/mol/K.
• [A] es la concentración molar de A en la unidad mol/L,
• [B] es la concentración molar de B en la unidad mol/L.

El producto zρ es equivalente al factor preexponencial de la ecuación de Arrhenius .

Validez de la teoría y factor estérico

Una vez formulada una teoría, es necesario probar su validez, es decir, comparar sus predicciones con los resultados de los experimentos.

Cuando se compara la forma de expresión de la constante de velocidad con la ecuación de velocidad para una reacción bimolecular elemental, , se observa que ${\displaystyle r=k(T)[A][B]}$

${\displaystyle k(T)=N_{A}\sigma _{AB}\rho {\sqrt {\frac {8k_{\text{B}}T}{\pi \mu _{AB}}}}\exp \left({\frac {-E_{\text{a}}}{RT}}\right)}$

unidad M ⁻¹ ⋅s ⁻¹ (= dm ³ ⋅mol ⁻¹ ⋅s ⁻¹ ), con todas las unidades de dimensión dm incluyendo k _B .

Esta expresión es similar a la ecuación de Arrhenius y da la primera explicación teórica de la ecuación de Arrhenius sobre una base molecular. La débil dependencia de la temperatura del factor preexponencial es tan pequeña en comparación con el factor exponencial que no se puede medir experimentalmente, es decir, "no es factible establecer, sobre la base de estudios de temperatura de la constante de velocidad, si la T predicha ^⁠1/2⁠ La dependencia del factor preexponencial se observa experimentalmente". ^[9]

Factor estérico

Si se comparan los valores de las constantes de velocidad predichas con los valores de las constantes de velocidad conocidas, se observa que la teoría de colisiones no logra estimar las constantes correctamente, y cuanto más complejas son las moléculas, más falla. La razón de esto es que se ha supuesto que las partículas son esféricas y capaces de reaccionar en todas las direcciones, lo cual no es cierto, ya que la orientación de las colisiones no siempre es la adecuada para la reacción. Por ejemplo, en la reacción de hidrogenación del etileno, la molécula de H ₂ debe aproximarse a la zona de enlace entre los átomos, y solo unas pocas de todas las colisiones posibles cumplen este requisito.

Para paliar este problema, es necesario introducir un nuevo concepto: el factor estérico ρ . Se define como la relación entre el valor experimental y el predicho (o la relación entre el factor de frecuencia y la frecuencia de colisión):

${\displaystyle \rho ={\frac {A_{\text{observed}}}{Z_{\text{calculated}}}},}$

y la mayoría de las veces es menor que la unidad. ^[7]

Generalmente, cuanto más complejas sean las moléculas de los reactivos, menor será el factor estérico. Sin embargo, algunas reacciones presentan factores estéricos mayores que la unidad: las reacciones de arpón , en las que los átomos intercambian electrones , produciendo iones . La desviación de la unidad puede tener diferentes causas: las moléculas no son esféricas, por lo que son posibles diferentes geometrías; no toda la energía cinética se entrega en el lugar correcto; la presencia de un disolvente (cuando se aplica a las soluciones), etc.

La teoría de colisiones se puede aplicar a reacciones en solución; en ese caso, la jaula del disolvente tiene un efecto sobre las moléculas reactivas y pueden ocurrir varias colisiones en un solo encuentro, lo que lleva a que los factores preexponenciales predichos sean demasiado grandes. Los valores de ρ mayores que la unidad se pueden atribuir a contribuciones entrópicas favorables.

Modelos alternativos de colisión para soluciones diluidas

La colisión en un gas diluido o en una solución líquida está regulada por la difusión en lugar de por colisiones directas, que se pueden calcular a partir de las leyes de difusión de Fick . Marian Smoluchowski propuso modelos teóricos para calcular la frecuencia de colisión en soluciones en una publicación seminal de 1916 en el límite de tiempo infinito ^[4] y Jixin Chen en 2022 en una aproximación de tiempo finito ^[5] . En la figura de la derecha se muestra un esquema de comparación de las ecuaciones de velocidad en gas puro y solución.

Un esquema que compara la colisión directa y la colisión difusiva, con las ecuaciones de velocidad correspondientes.

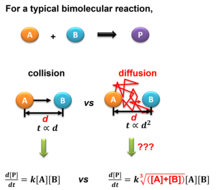
Para una solución diluida en fase gaseosa o líquida, la ecuación de colisión desarrollada para gas puro no es adecuada cuando la difusión toma el control de la frecuencia de colisión, es decir, la colisión directa entre las dos moléculas ya no domina. Para cualquier molécula A dada, tiene que colisionar con muchas moléculas de solvente, digamos la molécula C, antes de encontrar la molécula B con la que reaccionar. Por lo tanto, la probabilidad de colisión debe calcularse utilizando el modelo de movimiento browniano , que puede aproximarse a un flujo difusivo utilizando varias condiciones de contorno que producen diferentes ecuaciones en el modelo de Smoluchowski y el modelo de JChen.

Para la colisión difusiva, en el límite de tiempo infinito cuando el flujo molecular puede calcularse a partir de las leyes de difusión de Fick , en 1916 Smoluchowski derivó una frecuencia de colisión entre las moléculas A y B en una solución diluida: ^[4]

${\displaystyle Z_{AB}=4\pi RD_{r}C_{A}C_{B}}$

dónde:

• ${\displaystyle Z_{AB}}$es la frecuencia de colisión, unidad #colisiones/s en 1 m ³ de solución.
• ${\displaystyle R}$es el radio de la sección transversal de colisión, unidad m.
• ${\displaystyle D_{r}}$es la constante de difusión relativa entre A y B, unidad m ² /s, y . ${\displaystyle D_{r}=D_{A}+D_{B}}$
• ${\displaystyle C_{A}}$y son las concentraciones numéricas de las moléculas A y B en la solución respectivamente, unidad #molécula/m ³ . ${\displaystyle C_{B}}$

o

${\displaystyle Z_{AB}=1000N_{A}*4\pi RD_{r}[A][B]=k[A][B]}$

dónde:

• ${\displaystyle Z_{AB}}$se expresa en colisiones molares por segundo en 1 L de solución.
• ${\displaystyle N_{\text{A}}}$es la constante de Avogadro .
• ${\displaystyle R}$es el radio de la sección transversal de colisión, unidad m.
• ${\displaystyle D_{r}}$es la constante de difusión relativa entre A y B, unidad m ² /s.
• ${\displaystyle [A]}$y son las concentraciones molares de A y B respectivamente, unidad mol/L. ${\displaystyle [B]}$
• ${\displaystyle k}$es la constante de velocidad de colisión difusiva, unidad L mol ⁻¹ s ⁻¹ .

Ha habido muchas ampliaciones y modificaciones al modelo Smoluchowski desde que fue propuesto en 1916.

En 2022, Chen argumenta que, debido a que el flujo difusivo evoluciona con el tiempo y la distancia entre las moléculas tiene un valor finito a una concentración dada, debería haber un tiempo crítico para cortar la evolución del flujo que dará un valor mucho mayor que la solución infinita que Smoluchowski ha propuesto. ^[5] Por lo tanto, propone utilizar el tiempo promedio para que dos moléculas cambien de lugar en la solución como el tiempo de corte crítico, es decir, el tiempo de visita del primer vecino. Aunque un tiempo alternativo podría ser el tiempo medio de trayectoria libre o el tiempo medio del primer pasajero, sobrestima el gradiente de concentración entre la ubicación original del primer pasajero y el objetivo. Esta hipótesis produce una ecuación de velocidad cinética de reacción fractal de colisión difusiva en una solución diluida: ^[5]

${\displaystyle Z_{AB}=(1000N_{A})^{4/3}*8\pi ^{-1}A\beta D_{r}([A]+[B])^{1/3}[A][B]=k([A]+[B])^{1/3}[A][B]}$

dónde:

• ${\displaystyle Z_{AB}}$se expresa en colisiones molares por segundo en 1 L de solución.
• ${\displaystyle N_{\text{A}}}$es la constante de Avogadro .
• ${\displaystyle A}$es el área de la sección transversal de colisión en la unidad m ² .
• ${\displaystyle \beta }$es el producto de las fracciones sin unidades del área superficial reactiva en A y B. es el área de la sección transversal de adsorción efectiva. ${\displaystyle \beta A}$
• ${\displaystyle D_{r}}$es la constante de difusión relativa entre A y B, unidad m ² /s, y . ${\displaystyle D_{r}=D_{A}+D_{B}}$
• ${\displaystyle [A]}$y son las concentraciones molares de A y B respectivamente, unidad mol/L. ${\displaystyle [B]}$
• ${\displaystyle k}$es la constante de velocidad de colisión difusiva, unidad L ^4/3 mol ^-4/3 s ⁻¹ .

Véase también

• Gas bidimensional
• Ecuación de velocidad

Referencias

1. Trautz, máx. Das Gesetz der Reaktionsgeschwindigkeit und der Gleichgewichte in Gasen. Bestätigung der Additivität von Cv − 3/2 R. Neue Bestimmung der Integrationskonstanten und der Moleküldurchmesser, Zeitschrift für anorganische und allgemeine Chemie, volumen 96, número 1, páginas 1 a 28, (1916).
2. IUPAC , Compendio de terminología química , 2.ª edición (el "Libro de oro") (1997). Versión corregida en línea: (2006–) "teoría de colisiones". doi :10.1351/goldbook.C01170
3. William Cudmore McCullagh Lewis, XLI.—Estudios en catálisis. Parte IX. El cálculo en medida absoluta de constantes de velocidad y constantes de equilibrio en sistemas gaseosos, J. Chem. Soc., Trans., 1918, 113, 471-492.
4. Smoluchowski, Marian (1916). "Drei Vorträge über Diffusion, Brownsche Molekularbewegung und Koagulation von Kolloidteilchen". Física. Z. (en alemán). 17 : 557–571, ​​585–599. Código Bib : 1916ZPhy...17..557S.
5. Chen, Jixin (2022). "¿Por qué el orden de reacción de una reacción bimolecular debería ser 2,33 en lugar de 2?". J. Phys. Chem. A . 126 : 9719–9725. doi :10.1021/acs.jpca.2c07500. PMC 9805503 . 
6. "6.1.6: La teoría de las colisiones". 2 de octubre de 2013.
7. IUPAC , Compendio de terminología química , 2.ª ed. (el "Libro de oro") (1997). Versión corregida en línea: (2006–) "factor estérico". doi :10.1351/goldbook.S05998
8. IUPAC , Compendio de terminología química , 2.ª ed. (el "Libro de oro") (1997). Versión corregida en línea: (2006–) "collision frequency". doi :10.1351/goldbook.C01166
9. Kenneth Connors, Cinética química, 1990, VCH Publishers.
10. EA Moelwyn-Hughes, La cinética de las reacciones en solución, 2.ª ed., página 71.

Enlaces externos

• Introducción a la teoría de colisiones