Relación simétrica

Tipo de relación binaria

Una relación simétrica es un tipo de relación binaria . Formalmente, una relación binaria R sobre un conjunto X es simétrica si: ^[1]

${\displaystyle \forall a,b\in X(aRb\Leftrightarrow bRa),}$

donde la notación aRb significa que ( a , b ) ∈ R .

Un ejemplo es la relación "es igual a", porque si a = b es verdadera entonces b = a también es verdadera. Si R ^T representa el inverso de R , entonces R es simétrico si y sólo si R = R ^T . ^[2]

La simetría, junto con la reflexividad y la transitividad , son las tres propiedades definitorias de una relación de equivalencia . ^[1]

Ejemplos

En matemáticas

• "es igual a" ( igualdad ) (mientras que "es menor que" no es simétrico)
• "es comparable a", para elementos de un conjunto parcialmente ordenado
• "... y... son impares":

Matemáticas fuera de la ley

• "está casado con" (en la mayoría de los sistemas legales)
• "es un hermano completamente biológico de"
• "es un homófono de"
• "es un compañero de trabajo de"
• "es un compañero de equipo de"

Relación con las relaciones asimétricas y antisimétricas

Relaciones simétricas y antisimétricas

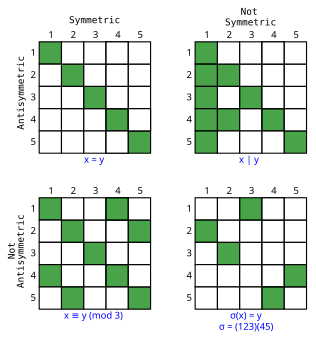
Por definición, una relación no vacía no puede ser a la vez simétrica y asimétrica (donde si a está relacionado con b , entonces b no puede estar relacionado con a (de la misma manera)). Sin embargo, una relación no puede ser ni simétrica ni asimétrica, que es el caso de "es menor o igual que" y "se aprovecha de").

Simétrico y antisimétrico (donde la única forma en que a puede estar relacionado con b y b con a es si a = b ) son en realidad independientes entre sí, como lo muestran estos ejemplos.

Propiedades

• Una relación simétrica y transitiva es siempre cuasireflexiva . ^[a]
• Una forma de contar las relaciones simétricas en n elementos, es que en su representación matricial binaria el triángulo superior derecho determina la relación completamente, y puede darse de forma arbitraria, por lo que hay tantas relaciones simétricas como n × n matrices binarias de triángulos superiores, 2 ^{n ( n +1)/2} . ^[3]

Téngase en cuenta que S ( n , k ) se refiere a números de Stirling del segundo tipo .

Notas

1. Si xRy , yRx por simetría, por lo tanto xRx por transitividad. La prueba de xRy ⇒ yRy es similar.

Referencias

1. Biggs, Norman L. (2002). Matemáticas discretas . Oxford University Press. pág. 57. ISBN 978-0-19-871369-2.
2. "MAD3105 1.2". Departamento de Matemáticas de la Universidad Estatal de Florida . Universidad Estatal de Florida . Consultado el 30 de marzo de 2024 .
3. Sloane, N. J. A. (ed.). "Secuencia A006125". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS.

Véase también

• Propiedad conmutativa  – Propiedad de algunas operaciones matemáticas
• Simetría en matemáticas
• Simetría  – Invariancia matemática bajo transformaciones