Equilibrio de conchas

Método de análisis de la velocidad del fluido a través de un flujo

En mecánica de fluidos , se puede utilizar un balance de capas para determinar el perfil de velocidad ^{[ ¿de qué? ]} , es decir, cómo cambia la velocidad del fluido con la posición a través de una sección transversal de flujo.

Una "capa" es un elemento diferencial del flujo. Al observar el momento y las fuerzas en una pequeña porción, es posible integrar el flujo para ver el panorama general del flujo en su conjunto. El equilibrio determina qué entra y sale de la capa. El momento se crea dentro de la capa a través del fluido que entra y sale de ella y por la tensión de corte . Además, hay presión y fuerzas gravitacionales sobre la capa. A partir de esto, es posible encontrar una velocidad para cualquier punto a lo largo del flujo.

Aplicaciones

Los balances de capas se pueden utilizar en muchas situaciones. Por ejemplo, el flujo en una tubería, el flujo de múltiples fluidos uno alrededor del otro o el flujo debido a la diferencia de presión. Aunque los términos en el balance de capas y las condiciones de contorno cambiarán, la configuración básica y el proceso son los mismos.

Requisitos para los cálculos del balance de la carcasa

El fluido debe presentar:

• Flujo laminar
• Sin curvas ni dobleces
• Estado estable
• Dos condiciones de contorno

Las condiciones de contorno se utilizan para encontrar constantes de integración.

• Límite fluido - sólido : Condición sin deslizamiento , la velocidad de un líquido en un sólido es igual a la velocidad del sólido.
• Límite líquido - gas : Esfuerzo cortante = 0.
• Límite líquido-líquido: Igual velocidad y esfuerzo cortante en ambos líquidos.

Realizar balances de shell

Un fluido fluye entre y en contacto con dos superficies horizontales de área de contacto A. Se utiliza una capa diferencial de altura Δy (ver diagrama a continuación).

Diagrama del proceso de equilibrio de capas en mecánica de fluidos

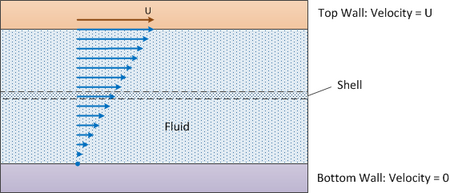
La superficie superior se mueve a una velocidad U y la superficie inferior está estacionaria.

• Densidad del fluido = ρ
• Viscosidad del fluido = μ
• La velocidad en la dirección x = , que se muestra mediante la línea diagonal anterior. Esto es lo que se calcula mediante un balance de capas. ${\displaystyle V_{x}}$

La conservación del momento es la clave del equilibrio de capas

• (Tasa de momento de entrada) - (tasa de momento de salida) + (suma de todas las fuerzas) = ​​0

Para realizar un balance de shell, siga los siguientes pasos básicos:

1. Halla el momento a partir de la tensión cortante. (Momento a partir de la tensión cortante que entra al sistema) - (Momento a partir de la tensión cortante que sale del sistema). El momento a partir de la tensión cortante entra en la capa en y y sale del sistema en y  + Δ y . Tensión cortante = τ _yx , área = A , momento = τ _yx A .
2. Halla el momento del flujo. El momento fluye hacia el sistema en x  = 0 y hacia afuera en x  = L. El flujo es de estado estable. Por lo tanto, el flujo de momento en x  = 0 es igual al momento del flujo en x  = L. Por lo tanto, estos se cancelan.
3. Encuentra la fuerza de gravedad sobre la concha.
4. Encuentra fuerzas de presión .
5. Sustituya la conservación del momento por τ _yx .
6. Aplicar la ley de viscosidad de Newton para un fluido newtoniano τ _yx = - μ ( dV _x / dy ).
7. Integre para encontrar la ecuación de velocidad y utilice las condiciones de contorno para encontrar constantes de integración.

Límite 1: Superficie superior: y = 0 y V _x = U

Límite 2: Superficie inferior: y = D y V _x = 0

Para obtener ejemplos de cómo realizar balances de shell, visite los recursos que se enumeran a continuación.

Recursos

• "Soluciones de problemas en fenómenos de transporte: problemas de mecánica de fluidos" . Consultado el 6 de octubre de 2007 .

• Harriott, Peter; W. McCabe; J. Smith (2004). Operaciones unitarias de ingeniería química: séptima edición. McGraw-Hill Professional. págs. 68–132. ISBN 9780072848236.