stringtranslate.com

SHA-2

SHA-2 ( Secure Hash Algorithm 2 ) es un conjunto de funciones hash criptográficas diseñadas por la Agencia de Seguridad Nacional de los Estados Unidos (NSA) y publicadas por primera vez en 2001. [3] [4] Se construyen utilizando la construcción Merkle–Damgård , a partir de una función de compresión unidireccional construida a su vez utilizando la estructura Davies–Meyer a partir de un cifrador de bloques especializado.

SHA-2 incluye cambios significativos con respecto a su predecesor, SHA-1 . La familia SHA-2 consta de seis funciones hash con resúmenes (valores hash) de 224, 256, 384 o 512 bits: [5] SHA-224, SHA-256, SHA-384, SHA-512, SHA-512/224, SHA-512/256 . SHA-256 y SHA-512 son nuevas funciones hash cuyos resúmenes son ocho palabras de 32 y 64 bits, respectivamente. Utilizan diferentes cantidades de desplazamiento y constantes aditivas, pero sus estructuras son prácticamente idénticas, y solo difieren en el número de rondas. SHA-224 y SHA-384 son versiones truncadas de SHA-256 y SHA-512 respectivamente, calculadas con diferentes valores iniciales. SHA-512/224 y SHA-512/256 también son versiones truncadas de SHA-512, pero los valores iniciales se generan utilizando el método descrito en los Estándares Federales de Procesamiento de Información (FIPS) PUB 180-4.

SHA-2 fue publicado por primera vez por el Instituto Nacional de Estándares y Tecnología (NIST) como un estándar federal de EE. UU. La familia de algoritmos SHA-2 está patentada en EE. UU. [6] Estados Unidos ha publicado la patente bajo una licencia libre de regalías . [5]

A partir de 2011, los mejores ataques públicos rompen la resistencia de preimagen para 52 de 64 rondas de SHA-256 o 57 de 80 rondas de SHA-512, y la resistencia de colisión para 46 de 64 rondas de SHA-256. [1] [2]

Estándar hash

Una iteración en una función de compresión de la familia SHA-2. Los componentes azules realizan las siguientes operaciones: La rotación bit a bit utiliza constantes diferentes para SHA-512. Los números dados son para SHA-256. El rojo es la suma módulo 2 32 para SHA-256 o 2 64 para SHA-512.
    
    
    
    

Con la publicación de FIPS PUB 180-2, el NIST agregó tres funciones hash adicionales a la familia SHA. Los algoritmos se conocen colectivamente como SHA-2, llamados así por la longitud de sus resúmenes (en bits): SHA-256, SHA-384 y SHA-512.

Los algoritmos se publicaron por primera vez en 2001 en el borrador FIPS PUB 180-2, momento en el que se aceptaron la revisión y los comentarios públicos. En agosto de 2002, FIPS PUB 180-2 se convirtió en el nuevo estándar de hash seguro , reemplazando a FIPS PUB 180-1, que se publicó en abril de 1995. El estándar actualizado incluía el algoritmo SHA-1 original, con una notación técnica actualizada coherente con la que describe el funcionamiento interno de la familia SHA-2. [4]

En febrero de 2004, se publicó un aviso de cambio para FIPS PUB 180-2, especificando una variante adicional, SHA-224, definida para coincidir con la longitud de clave de Triple DES de dos claves . [7] En octubre de 2008, el estándar se actualizó en FIPS PUB 180-3, incluyendo SHA-224 del aviso de cambio, pero por lo demás sin realizar cambios fundamentales en el estándar. La motivación principal para actualizar el estándar fue reubicar la información de seguridad sobre los algoritmos hash y las recomendaciones para su uso en las Publicaciones Especiales 800-107 y 800-57. [8] [9] [10] Los datos de prueba detallados y los resúmenes de mensajes de ejemplo también se eliminaron del estándar y se proporcionaron como documentos separados. [11]

En enero de 2011, el NIST publicó SP800-131A, que especificaba un paso del mínimo vigente en ese momento de seguridad de 80 bits (proporcionada por SHA-1) permitido para el uso del gobierno federal hasta fines de 2013, a una seguridad de 112 bits (proporcionada por SHA-2) que es tanto el requisito mínimo (a partir de 2014) como el nivel de seguridad recomendado (a partir de la fecha de publicación en 2011). [12]

En marzo de 2012, el estándar se actualizó en FIPS PUB 180-4, agregando las funciones hash SHA-512/224 y SHA-512/256, y describiendo un método para generar valores iniciales para versiones truncadas de SHA-512. Además, se eliminó una restricción sobre el relleno de los datos de entrada antes del cálculo del hash, lo que permite que los datos hash se calculen simultáneamente con la generación de contenido, como una transmisión de audio o video en tiempo real. El relleno del bloque de datos final aún debe ocurrir antes de la salida del hash. [13]

En julio de 2012, el NIST revisó la SP800-57, que proporciona orientación para la gestión de claves criptográficas. La publicación prohibió la creación de firmas digitales con una seguridad de hash inferior a 112 bits después de 2013. La revisión anterior, de 2007, especificó que la fecha límite sería finales de 2010. [10] En agosto de 2012, el NIST revisó la SP800-107 de la misma manera. [9]

La competencia de funciones hash del NIST seleccionó una nueva función hash, SHA-3 , en 2012. [14] El algoritmo SHA-3 no se deriva de SHA-2.

Aplicaciones

La función hash SHA-2 se implementa en algunas aplicaciones y protocolos de seguridad ampliamente utilizados, incluidos TLS y SSL , PGP , SSH , S/MIME e IPsec . La demanda computacional inherente de los algoritmos SHA-2 ha impulsado la propuesta de soluciones más eficientes, como las basadas en aceleradores de hardware de circuitos integrados específicos de la aplicación (ASIC). [15]

SHA-256 se utiliza para autenticar paquetes de software Debian [16] y en el estándar de firma de mensajes DKIM ; SHA-512 es parte de un sistema para autenticar videos de archivo del Tribunal Penal Internacional del genocidio de Ruanda . [17] Se propone el uso de SHA-256 y SHA-512 en DNSSEC . [18] Los proveedores de Unix y Linux están pasando a utilizar SHA-2 de 256 y 512 bits para el hash seguro de contraseñas. [19]

Varias criptomonedas , incluida Bitcoin , utilizan SHA-256 para verificar transacciones y calcular la prueba de trabajo [20] o prueba de participación . [21] El auge de los chips aceleradores ASIC SHA-2 ha llevado al uso de esquemas de prueba de trabajo basados ​​en scrypt .

SHA-1 y SHA-2 son los algoritmos de hash seguros que la ley exige para su uso en ciertas aplicaciones del gobierno de los EE. UU. , incluido el uso dentro de otros algoritmos y protocolos criptográficos, para la protección de información confidencial no clasificada. La FIPS PUB 180-1 también fomentaba la adopción y el uso de SHA-1 por parte de organizaciones privadas y comerciales. SHA-1 se está retirando de la mayoría de los usos gubernamentales; el Instituto Nacional de Estándares y Tecnología de los EE. UU. dice: "Las agencias federales deben dejar de usar SHA-1 para... aplicaciones que requieren resistencia a colisiones tan pronto como sea posible, y deben usar la familia de funciones hash SHA-2 para estas aplicaciones después de 2010" (énfasis en el original). [22] Se esperaba que la directiva del NIST de que las agencias del gobierno de los EE. UU. deberían, pero no deben explícitamente, dejar de usar SHA-1 después de 2010 [23] acelerara la migración hacia el abandono de SHA-1.

Las funciones SHA-2 no se adoptaron rápidamente inicialmente, a pesar de una mejor seguridad que SHA-1. Las razones pueden incluir la falta de soporte para SHA-2 en sistemas que ejecutan Windows XP SP2 o anterior [24] y una falta de urgencia percibida ya que aún no se habían encontrado colisiones SHA-1. El equipo de Google Chrome anunció un plan para hacer que su navegador web deje de respetar gradualmente los certificados TLS dependientes de SHA-1 durante un período desde fines de 2014 y principios de 2015. [25] [26] [27] De manera similar, Microsoft anunció [28] que Internet Explorer y Edge dejarían de respetar los certificados TLS públicos firmados con SHA-1 a partir de febrero de 2017. Mozilla deshabilitó SHA-1 a principios de enero de 2016, pero tuvo que volver a habilitarlo temporalmente a través de una actualización de Firefox , después de problemas con las interfaces de usuario basadas en web de algunos modelos de enrutadores y dispositivos de seguridad . [29]

Criptoanálisis y validación

Para una función hash para la cual L es el número de bits en el resumen del mensaje , encontrar un mensaje que corresponda a un resumen de mensaje dado siempre se puede hacer usando una búsqueda de fuerza bruta en 2 evaluaciones L. Esto se llama ataque de preimagen y puede o no ser práctico dependiendo de L y del entorno informático particular. El segundo criterio, encontrar dos mensajes diferentes que produzcan el mismo resumen de mensaje, conocido como colisión , requiere en promedio solo 2 evaluaciones L /2 usando un ataque de cumpleaños .

Algunas de las aplicaciones que utilizan hashes criptográficos, como el almacenamiento de contraseñas, se ven mínimamente afectadas por un ataque de colisión . La construcción de una contraseña que funcione para una cuenta determinada requiere un ataque de preimagen, así como el acceso al hash de la contraseña original (normalmente en el shadowarchivo), que puede ser trivial o no. La reversión del cifrado de contraseñas (por ejemplo, para obtener una contraseña para probarla en la cuenta de un usuario en otro lugar) no es posible gracias a los ataques. (Sin embargo, incluso un hash de contraseña seguro no puede evitar los ataques de fuerza bruta a contraseñas débiles ).

En el caso de la firma de documentos, un atacante no podría simplemente falsificar una firma de un documento existente; el atacante tendría que producir un par de documentos, uno inocuo y otro dañino, y lograr que el poseedor de la clave privada firmara el documento inocuo. Existen circunstancias prácticas en las que esto es posible; hasta fines de 2008, era posible crear certificados SSL falsificados utilizando una colisión MD5 que sería aceptada por los navegadores web más utilizados. [30]

El creciente interés en el análisis de hash criptográfico durante la competición SHA-3 produjo varios ataques nuevos a la familia SHA-2, los mejores de los cuales se muestran en la siguiente tabla. Sólo los ataques de colisión son de complejidad práctica; ninguno de los ataques se extiende a la función hash de ronda completa.

En FSE 2012, los investigadores de Sony dieron una presentación en la que sugerían que los ataques de pseudocolisión podrían extenderse a 52 rondas en SHA-256 y 57 rondas en SHA-512 basándose en el ataque de pseudopreimagen biclique . [31]

Validación oficial

Las implementaciones de todas las funciones de seguridad aprobadas por FIPS pueden validarse oficialmente a través del programa CMVP , dirigido conjuntamente por el Instituto Nacional de Estándares y Tecnología (NIST) y el Establecimiento de Seguridad de las Comunicaciones (CSE). Para la verificación informal, se encuentra disponible para su descarga en el sitio del NIST un paquete para generar una gran cantidad de vectores de prueba; sin embargo, la verificación resultante no reemplaza la validación formal del CMVP, que es requerida por ley [ cita requerida ] para ciertas aplicaciones.

A diciembre de 2013, hay más de 1300 implementaciones validadas de SHA-256 y más de 900 de SHA-512, y solo 5 de ellas son capaces de manejar mensajes con una longitud en bits no múltiplo de ocho y al mismo tiempo admiten ambas variantes. [40]

Vectores de prueba

Valores hash de una cadena vacía (es decir, un texto de entrada de longitud cero).

SHA224("")0x d14a028c2a3a2bc9476102bb288234c415a2b01f828ea62ac5b3e42fSHA256("")0x e3b0c44298fc1c149afbf4c8996fb92427ae41e4649b934ca495991b7852b855SHA384("")0x 38b060a751ac96384cd9327eb1b1e36a21fdb71114be07434c0cc7bf63f6e1da274edebfe76f65fbd51ad2f14898b95bSHA512("")0x cf83e1357eefb8bdf1542850d66d8007d620e4050b5715dc83f4a921d36ce9ce 47d0d13c5d85f2b0ff8318d2877eec2f63b931bd47417a81a538327af927da3eSHA512/224("")0x 6ed0dd02806fa89e25de060c19d3ac86cabb87d6a0ddd05c333b84f4SHA512/256("")0x c672b8d1ef56ed28ab87c3622c5114069bdd3ad7b8f9737498d0c01ecef0967a

Incluso un pequeño cambio en el mensaje dará como resultado (con una probabilidad abrumadora) un hash diferente, debido al efecto avalancha . Por ejemplo, agregar un punto al final de la siguiente oración cambia aproximadamente la mitad (111 de 224) de los bits del hash, lo que equivale a elegir un nuevo hash al azar:

SHA224(" El rápido zorro marrón salta sobre el perro perezoso ")0x730e109bd7a8a32b1cb9d9a09aa2325d2430587ddbc0c38bad911525SHA224(" El rápido zorro marrón salta sobre el perro perezoso . ")0x619cba8e8e05826e9b8c519c0a5c68f4fb653e8a3d8aa04bb2c8cd4c

Pseudocódigo

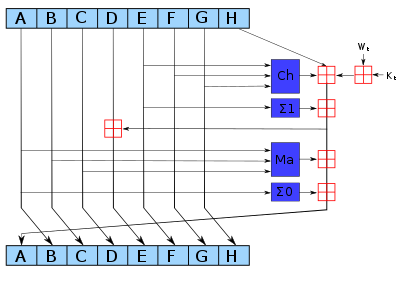
A continuación se muestra el pseudocódigo del algoritmo SHA-256. Observe el gran aumento en la mezcla entre los bits de las w[16..63]palabras en comparación con SHA-1.

Nota 1: Todas las variables son enteros sin signo de 32 bits y la adición se calcula módulo 2 32 Nota 2: Para cada ronda, hay una constante de ronda k[i] y una entrada en la matriz de programación de mensajes w[i], 0 ≤ i ≤ 63 Nota 3: La función de compresión utiliza 8 variables de trabajo, de a a h Nota 4: La convención big-endian se utiliza al expresar las constantes en este pseudocódigo y al analizar los datos del bloque de mensajes de bytes a palabras, por ejemplo, la primera palabra del mensaje de entrada "abc" después del relleno es 0x61626380  Inicializar valores hash: (primeros 32 bits de las partes fraccionarias de las raíces cuadradas de los primeros 8 primos 2..19):h0 := 0x6a09e667h1 := 0xbb67ae85h2 := 0x3c6ef372h3 := 0xa54ff53ah4 := 0x510e527fh5 := 0x9b05688ch6 := 0x1f83d9abh7 := 0x5be0cd19Inicializar matriz de constantes redondeadas: (primeros 32 bits de las partes fraccionarias de las raíces cúbicas de los primeros 64 primos 2..311):k[0..63] := 0x428a2f98, 0x71374491, 0xb5c0fbcf, 0xe9b5dba5, 0x3956c25b, 0x59f111f1, 0x923f82a4, 0xab1c5ed5, 0xd807aa98, 0x12835b01, 0x243185be, 0x550c7dc3, 0x72be5d74, 0x80deb1fe, 0x9bdc06a7, 0xc19bf174, 0xe49b69c1, 0xefbe4786, 0x0fc19dc6, 0x240ca1cc, 0x2de92c6f, 0x4a7484aa, 0x5cb0a9dc, 0x76f988da, 0x983e5152, 0xa831c66d, 0xb00327c8, 0xbf597fc7, 0xc6e00bf3, 0xd5a79147, 0x06ca6351, 0x14292967, 0x27b70a85, 0x2e1b2138, 0x4d2c6dfc, 0x53380d13, 0x650a7354, 0x766a0abb, 0x81c2c92e, 0x92722c85, 0xa2bfe8a1, 0xa81a664b, 0xc24b8b70, 0xc76c51a3, 0xd192e819, 0xd6990624, 0xf40e3585, 0x106aa070, 0x19a4c116, 0x1e376c08, 0x2748774c, 0x34b0bcb5, 0x391c0cb3, 0x4ed8aa4a, 0x5b9cca4f, 0x682e6ff3, 0x748f82ee, 0x78a5636f, 0x84c87814, 0x8cc70208, 0x90befffa, 0xa4506ceb, 0xbef9a3f7, 0xc67178f2Preprocesamiento (relleno):Comience con el mensaje original de longitud L bitsañadir un solo bit '1'añadir K bits '0', donde K es el número mínimo >= 0 tal que (L + 1 + K + 64) es un múltiplo de 512Anexar L como un entero big-endian de 64 bits, lo que hace que la longitud total posprocesada sea un múltiplo de 512 bitsde modo que los bits del mensaje sean: <mensaje original de longitud L> 1 <K ceros> <L como entero de 64 bits>, (el número de bits será un múltiplo de 512)Procesar el mensaje en fragmentos sucesivos de 512 bits:dividir el mensaje en fragmentos de 512 bitspara cada trozo Crea una matriz de programación de mensajes de 64 entradas w[0..63] de palabras de 32 bits (Los valores iniciales en w[0..63] no importan, por lo que muchas implementaciones los ponen a cero aquí) Copiar fragmento en las primeras 16 palabras w[0..15] de la matriz de programación de mensajes Amplíe las primeras 16 palabras en las 48 palabras restantes w[16..63] de la matriz de programación de mensajes:  para i de 16 a 63 s0 := (w[i-15] rotación a la derecha 7) xor (w[i-15] rotación a la derecha 18) xor (w[i-15] desplazamiento a la derecha 3) s1 := (w[i-2] rotación a la derecha 17) xor (w[i-2] rotación a la derecha 19) xor (w[i-2] desplazamiento a la derecha 10) w[i] := w[i-16] + s0 + w[i-7] + s1 Inicializar las variables de trabajo al valor hash actual: a := h0 b := h1 c := h2 d:=h3 y := h4 f := h5 g := h6 h7:= Función de compresión del bucle principal:  para i de 0 a 63 S1 := (e girar a la derecha 6) xor (e girar a la derecha 11) xor (e girar a la derecha 25) ch := (e y f) xor (( no e) y g) temp1 := h + S1 + ch + k[i] + w[i] S0 := ( rotación a la derecha 2) xor ( rotación a la derecha 13) xor ( rotación a la derecha 22) maj := (a y b) xor (a y c) xor (b y c) temp2 := S0 + mayor  h := g g := f f := e e := d + temp1 d := c c := b b := un a := temp1 + temp2 Agregue el fragmento comprimido al valor hash actual: h0 := h0 + a h1 := h1 + b h2 := h2 + c h3 := h3 + d h4 := h4 + e h5 := h5 + f h6 := h6 + g h7 := h7 + hProducir el valor hash final (big-endian):
digest := hash := h0 append h1 append h2 append h3 append h4 append h5 append h6 append h7

El cálculo de los valores chy majse puede optimizar de la misma manera que se describe para SHA-1 .

SHA-224 es idéntico a SHA-256, excepto que:

Valores hash iniciales SHA-224 (en big endian): (Los segundos 32 bits de las partes fraccionarias de las raíces cuadradas de los primos 9.º a 16.º 23..53)h[0..7] := 0xc1059ed8, 0x367cd507, 0x3070dd17, 0xf70e5939, 0xffc00b31, 0x68581511, 0x64f98fa7, 0xbefa4fa4

SHA-512 es idéntico en estructura a SHA-256, pero:

Valores hash iniciales SHA-512 (en big-endian):h[0..7] := 0x6a09e667f3bcc908, 0xbb67ae8584caa73b, 0x3c6ef372fe94f82b, 0xa54ff53a5f1d36f1, 0x510e527fade682d1, 0x9b05688c2b3e6c1f, ​​0x1f83d9abfb41bd6b, 0x5be0cd19137e2179Constantes de ronda SHA-512:k[0..79] := 0x428a2f98d728ae22, 0x7137449123ef65cd, 0xb5c0fbcfec4d3b2f, 0xe9b5dba58189dbbc, 0x3956c25bf348b538, 0x59f111f1b605d019, 0x923f82a4af194f9b, 0xab1c5ed5da6d8118, 0xd807aa98a3030242, 0x12835b0145706fbe, 0x243185be4ee4b28c, 0x550c7dc3d5ffb4e2, 0x72be5d74f27b896f, 0x80deb1fe3b1696b1, 0x9bdc06a725c71235, 0xc19bf174cf692694, 0xe49b69c19ef14ad2, 0xefbe4786384f25e3, 0x0fc19dc68b8cd5b5, 0x240ca1cc77ac9c65, 0x2de92c6f592b0275, 0x4a7484aa6ea6e483, 0x5cb0a9dcbd41fbd4, 0x76f988da831153b5, 0x983e5152ee66dfab, 0xa831c66d2db43210, 0xb00327c898fb213f, 0xbf597fc7beef0ee4, 0xc6e00bf33da88fc2, 0xd5a79147930aa725, 0x06ca6351e003826f, 0x142929670a0e6e70, 0x27b70a8546d22ffc, 0x2e1b21385c26c926, 0x4d2c6dfc5ac42aed, 0x53380d139d95b3df, 0x650a73548baf63de, 0x766a0abb3c77b2a8, 0x81c2c92e47edaee6, 0x92722c851482353b, 0xa2bfe8a14cf10364, 0xa81a664bbc423001, 0xc24b8b70d0f89791, 0xc76c51a30654be30, 0xd192e819d6ef5218, 0xd69906245565a910, 0xf40e35855771202a, 0x106aa07032bbd1b8, 0x19a4c116b8d2d0c8, 0x1e376c085141ab53, 0x2748774cdf8eeb99, 0x34b0bcb5e19b48a8, 0x391c0cb3c5c95a63, 0x4ed8aa4ae3418acb, 0x5b9cca4f7763e373, 0x682e6ff3d6b2b8a3, 0x748f82ee5defb2fc, 0x78a5636f43172f60, 0x84c87814a1f0ab72, 0x8cc702081a6439ec, 0x90befffa23631e28, 0xa4506cebde82bde9, 0xbef9a3f7b2c67915, 0xc67178f2e372532b, 0xca273eceea26619c, 0xd186b8c721c0c207, 0xeada7dd6cde0eb1e, 0xf57d4f7fee6ed178, 0x06f067aa72176fba, 0x0a637dc5a2c898a6, 0x113f9804bef90dae, 0x1b710b35131c471b, 0x28db77f523047d84, 0x32caab7b40c72493, 0x3c9ebe0a15c9bebc, 0x431d67c49c100d4c, 0x4cc5d4becb3e42b6, 0x597f299cfc657e2a, 0x5fcb6fab3ad6faec, 0x6c44198c4a475817SHA-512 Suma y Sigma:S0 := (una rotación a la derecha 28) xor (una rotación a la derecha 34) xor (una rotación a la derecha 39)S1 := (e girar a la derecha 14) xor (e girar a la derecha 18) xor (e girar a la derecha 41)s0 := (w[i-15] rotación a la derecha 1) xor (w[i-15] rotación a la derecha 8) xor (w[i-15] desplazamiento a la derecha 7)s1 := (w[i-2] rotación a la derecha 19) xor (w[i-2] rotación a la derecha 61) xor (w[i-2] desplazamiento a la derecha 6)

SHA-384 es idéntico a SHA-512, excepto que:

Valores hash iniciales SHA-384 (en big-endian):h[0..7] := 0xcbbb9d5dc1059ed8, 0x629a292a367cd507, 0x9159015a3070dd17, 0x152fecd8f70e5939, 0x67332667ffc00b31, 0x8eb44a8768581511, 0xdb0c2e0d64f98fa7, 0x47b5481dbefa4fa4

SHA-512/t es idéntico a SHA-512 excepto que:

La función de generación SHA-512/t IV evalúa un SHA-512 modificado en la cadena ASCII "SHA-512/ t ", sustituida por la representación decimal de t . El SHA-512 modificado es el mismo que el SHA-512, excepto que sus valores iniciales h0a t h7se han sometido a una operación XOR con la constante hexadecimal 0xa5a5a5a5a5a5a5a5.

Se puede encontrar un ejemplo de implementación en C para la familia de funciones hash SHA-2 en RFC 6234.

Comparación de funciones SHA

En la siguiente tabla, el estado interno significa la "suma hash interna" después de cada compresión de un bloque de datos.

En la columna de operaciones bit a bit, "Rot" significa rotación sin acarreo y "Shr" significa desplazamiento lógico a la derecha . Todos estos algoritmos emplean la adición modular de alguna manera, excepto SHA-3.

En la siguiente tabla se ofrecen mediciones de rendimiento más detalladas de las arquitecturas de procesadores modernas.

Los números de rendimiento etiquetados como 'x86' se ejecutaban utilizando código de 32 bits en procesadores de 64 bits, mientras que los números 'x86-64' son código nativo de 64 bits. Si bien SHA-256 está diseñado para cálculos de 32 bits, se beneficia del código optimizado para procesadores de 64 bits en la arquitectura x86. Las implementaciones de 32 bits de SHA-512 son significativamente más lentas que sus contrapartes de 64 bits. Las variantes de ambos algoritmos con diferentes tamaños de salida funcionarán de manera similar, ya que las funciones de expansión y compresión de mensajes son idénticas, y solo los valores hash iniciales y los tamaños de salida son diferentes. Las mejores implementaciones de MD5 y SHA-1 funcionan entre 4,5 y 6 ciclos por byte en procesadores modernos.

Las pruebas fueron realizadas por la Universidad de Illinois en Chicago en su sistema hydra8 ejecutando un Intel Xeon E3-1275 V2 a una velocidad de reloj de 3,5 GHz, y en su sistema hydra9 ejecutando una APU AMD A10-5800K a una velocidad de reloj de 3,8 GHz. [46] Las velocidades de ciclos por byte a las que se hace referencia anteriormente son el rendimiento medio de un algoritmo que digiere un mensaje de 4096 bytes utilizando el software de evaluación comparativa criptográfica SUPERCOP. [47] El rendimiento de MiB/s se extrapola a partir de la velocidad de reloj de la CPU en un solo núcleo; el rendimiento en el mundo real variará debido a una variedad de factores.

Implementaciones

A continuación se muestra una lista de bibliotecas de criptografía que admiten SHA-2:

La aceleración de hardware es proporcionada por las siguientes extensiones de procesador:

Véase también

Wikifunctions tiene una función SHA-256 .
Wikifunctions tiene una función SHA-384 .
Wikifunctions tiene una función SHA-512 .

Referencias

  1. ^ abc Dmitry Khovratovich, Christian Rechberger y Alexandra Savelieva (2011). "Bicliques for Preimages: Attacks on Skein-512 and the SHA-2 family" (PDF) . Archivo de impresión electrónica de criptología de la IACR . 2011 (286). Archivado (PDF) desde el original el 15 de febrero de 2022 . Consultado el 15 de febrero de 2022 .
  2. ^ abc Mario Lamberger y Florian Mendel (2011). "Ataque diferencial de orden superior en SHA-256 reducido" (PDF) . Archivo de la edición electrónica de criptología de la IACR . 2011 (37). Archivado (PDF) desde el original el 22 de diciembre de 2022. Consultado el 15 de febrero de 2022 .
  3. ^ Penard, Wouter; van Werkhoven, Tim. "Sobre la familia de algoritmos de hash seguro" (PDF) . staff.science.uu.nl . Archivado desde el original (PDF) el 2016-03-30.
  4. ^ ab Aviso del Registro Federal 02-21599, que anuncia la aprobación de la publicación FIPS 180-2 Archivado el 14 de marzo de 2022 en Wayback Machine
  5. ^ ab "Detalles de propiedad intelectual: Estados Unidos de América representados por la declaración de licencia general de la Agencia de Seguridad Nacional". IETF Datatracker . 858. Archivado desde el original el 16 de junio de 2016 . Consultado el 17 de febrero de 2008 .
  6. ^ US 6829355, Lilly, Glenn M., "Dispositivo y método de hash criptográfico unidireccional", publicado el 7 de diciembre de 2004, asignado a la Agencia de Seguridad Nacional 
  7. ^ "FIPS 180-2 con Aviso de cambio 1" (PDF) . csrc.nist.gov . Archivado (PDF) desde el original el 2017-08-09 . Consultado el 2022-02-15 .
  8. ^ Aviso del Registro Federal E8-24743, que anuncia la aprobación de la publicación FIPS 180-3
  9. ^ ab Dang, Quynh (24 de agosto de 2012). Recomendación para aplicaciones que utilizan algoritmos hash aprobados (informe). Instituto Nacional de Estándares y Tecnología. Archivado desde el original el 28 de agosto de 2023. Consultado el 28 de agosto de 2023 .
  10. ^ ab Barker, Elaine; Barker, William; Burr, William; Polk, W.; Smid, Miles (10 de julio de 2012). Recomendación para la gestión de claves, parte 1: general (revisión 3) (informe). Instituto Nacional de Normas y Tecnología. Archivado desde el original el 28 de agosto de 2023. Consultado el 28 de agosto de 2023 .
  11. ^ "NIST.gov – División de Seguridad Informática – Centro de Recursos de Seguridad Informática". 29 de diciembre de 2016. Archivado desde el original el 9 de septiembre de 2017. Consultado el 15 de febrero de 2022 .
  12. ^ Barker, Elaine; Roginsky, Allen (13 de enero de 2011). Transiciones: recomendación para la transición del uso de algoritmos criptográficos y longitudes de clave (informe). Instituto Nacional de Estándares y Tecnología. Archivado desde el original el 28 de agosto de 2023. Consultado el 28 de agosto de 2023 .
  13. ^ Aviso del Registro Federal 2012-5400, que anuncia la aprobación de la publicación FIPS 180-4
  14. ^ "NIST selecciona al ganador del concurso de algoritmos de hash seguro (SHA-3)". NIST . 2 de octubre de 2012. Archivado desde el original el 2 de abril de 2015 . Consultado el 24 de febrero de 2015 .
  15. ^ Lucas Daudt Franck; Gabriel Augusto Ginja; João Paulo Carmo; José A. Alfonso; Maximiliam Luppé (2024). "Diseño ASIC personalizado para SHA-256 utilizando herramientas de código abierto". Computadoras . 13 (1): 9. doi : 10.3390/computers13010009 . hdl : 1822/89307 .
  16. ^ "Verificación de la autenticidad de las imágenes de Debian". Archivado desde el original el 19 de febrero de 2024. Consultado el 19 de febrero de 2024 .
  17. ^ Markoff, John (27 de enero de 2009). "Una herramienta para verificar registros digitales, incluso a medida que la tecnología cambia". The New York Times . ISSN  0362-4331. Archivado desde el original el 19 de septiembre de 2023 . Consultado el 27 de agosto de 2023 .
  18. ^ Uso de algoritmos SHA-2 con RSA en registros de recursos DNSKEY y RRSIG para DNSSEC. Octubre de 2009. doi : 10.17487/RFC5702 . RFC 5702.
  19. ^ "Cifrado Unix con SHA-256/512". akkadia.org . Archivado desde el original el 20 de agosto de 2023 . Consultado el 27 de agosto de 2023 .
  20. ^ Bitcoin, Excedente. "Bitcoin no desperdicia energía". Excedente de Bitcoin . Archivado desde el original el 2022-05-28 . Consultado el 2020-04-20 .
  21. ^ "¿Qué es SHA-256 y cómo se relaciona con Bitcoin? - Mycryptopedia". Mycryptopedia . 2017-09-21. Archivado desde el original el 2018-09-17 . Consultado el 2018-09-17 .
  22. ^ División de Seguridad Informática, Laboratorio de Tecnología de la Información (4 de enero de 2017). «Política del NIST sobre funciones hash – Funciones hash | CSRC | CSRC». CSRC | NIST . Archivado desde el original el 28 de agosto de 2023. Consultado el 27 de agosto de 2023 .
  23. ^ "Secure Hashing". NIST . Archivado desde el original el 25 de junio de 2011 . Consultado el 25 de noviembre de 2010 .
  24. ^ "Descripción general del Service Pack 3 de Windows XP" (PDF) . Microsoft Corporation. Archivado desde el original (PDF) el 30 de mayo de 2008.
  25. ^ "Desapareciendo gradualmente SHA-1". Blog de Chromium . Archivado desde el original el 2023-08-07 . Consultado el 2023-08-27 .
  26. ^ Eric Mill. "SHAAAAAAAAAAAAA". SHAAAAAAAAAAAAA.com . Archivado desde el original el 2017-03-01 . Consultado el 2015-08-26 .
  27. ^ "Preguntas frecuentes no oficiales sobre la descontinuación de SHA1 en Chrome". Filippo Valsorda . 2015-04-08. Archivado desde el original el 2023-08-28 . Consultado el 2023-08-27 .
  28. ^ "Una actualización de nuestra hoja de ruta para la descontinuación de SHA-1 – Blog de desarrollo de Microsoft EdgeBlog de desarrollo de Microsoft Edge". blogs.windows.com . 29 de abril de 2016. Archivado desde el original el 28 de noviembre de 2016 . Consultado el 28 de noviembre de 2016 .
  29. ^ en línea, heise (8 de enero de 2016). "Firefox: Mozilla schaltet SHA-1 ab… und direkt wieder an". Seguridad (en alemán). Archivado desde el original el 28 de agosto de 2023 . Consultado el 27 de agosto de 2023 .
  30. ^ Alexander Sotirov, Marc Stevens, Jacob Appelbaum, Arjen Lenstra, David Molnar, Dag Arne Osvik, Benne de Weger, MD5 considerado dañino hoy en día: creación de un certificado de CA fraudulento Archivado el 23 de marzo de 2022 en Wayback Machine . , consultado el 29 de marzo de 2009.
  31. ^ Ji Li, Takanori Isobe y Kyoji Shibutani, Laboratorio de investigación de Sony China y Sony Corporation, Conversión de un ataque de preimagen de encuentro en el medio en un ataque de pseudocolisión: aplicación a SHA-2 Archivado el 24 de febrero de 2022 en Wayback Machine.
  32. ^ Sanadhya, Somitra Kumar; Sarkar, Palash (2008), Nuevos ataques de colisión contra SHA-2 de hasta 24 pasos, Lecture Notes in Computer Science, vol. 5365, Springer-Verlag, págs. 91-103, doi :10.1007/978-3-540-89754-5_8, ISBN 978-3-540-89753-8, archivado desde el original el 21 de enero de 2022 , consultado el 12 de febrero de 2024
  33. ^ Sanadhya, Somitra Kumar; Sarkar, Palash (2009). "Un análisis combinatorio de ataques recientes a la familia SHA-2 de reducción gradual". Criptografía y comunicaciones . 1 (2): 135–173. doi :10.1007/s12095-009-0011-5. Archivado desde el original el 2023-08-02 . Consultado el 2024-02-12 .
  34. ^ Kazumaro Aoki; Jian Guo; Krystian Matusiewicz; Yu Sasaki y Lei Wang (2009). "Preimágenes para SHA-2 reducido por pasos". Avances en criptología – ASIACRYPT 2009. Apuntes de clase en informática. Vol. 5912. Springer Berlin Heidelberg. págs. 578–597. doi :10.1007/978-3-642-10366-7_34. ISBN 978-3-642-10366-7. ISSN  0302-9743.
  35. ^ Jian Guo; San Ling; Christian Rechberger y Huaxiong Wang (2010). "Ataques avanzados de preimagen de tipo Meet-in-the-Middle: primeros resultados en Full Tiger y resultados mejorados en MD4 y SHA-2". Avances en criptología - ASIACRYPT 2010 (PDF) . Apuntes de clase en informática. Vol. 6477. Springer Berlin Heidelberg. págs. 56–75. doi :10.1007/978-3-642-17373-8_4. ISBN 978-3-642-17373-8. ISSN  0302-9743. Archivado (PDF) desde el original el 2022-03-03 . Consultado el 2022-02-15 .
  36. ^ Florian Mendel; Tomislav Nad; Martin Schläffer (2013). "Mejora de las colisiones locales: nuevos ataques a SHA-256 reducido". Avances en criptología – EUROCRYPT 2013. Apuntes de clase en informática. Vol. 7881. Springer Berlin Heidelberg. págs. 262–278. doi :10.1007/978-3-642-38348-9_16. ISBN 978-3-642-38348-9. ISSN  0302-9743. Archivado desde el original el 6 de noviembre de 2018. Consultado el 13 de diciembre de 2014 .
  37. ^ Maria Eichlseder y Florian Mendel y Martin Schläffer (2014). "Heurísticas de ramificación en búsqueda de colisiones diferenciales con aplicaciones a SHA-512" (PDF) . Archivo de publicaciones electrónicas de criptología de la IACR . 2014 (302). Archivado (PDF) desde el original el 20 de enero de 2022 . Consultado el 15 de febrero de 2022 .
  38. ^ Christoph Dobraunig; Maria Eichlseder y Florian Mendel (2016). "Análisis de SHA-512/224 y SHA-512/256" (PDF) . Asociación Internacional de Investigación Criptológica . Archivado (PDF) desde el original el 2017-07-15 . Consultado el 2016-04-15 .
  39. ^ Li, Yingxin; Liu, Fukang; Wang, Gaoli (2024). "Nuevos récords en ataques de colisión en SHA-2". Archivo de ePrints de criptología . Archivado desde el original el 2024-03-02 . Consultado el 2024-03-02 .
  40. ^ "Lista de validación de SHS". NIST . 16 de junio de 2017. Archivado desde el original el 17 de junio de 2017.
  41. ^ "Tabla de medidas". bench.cr.yp.to .
  42. ^ Tao, Xie; Liu, Fanbao; Feng, Dengguo (2013). Ataque de colisión rápida en MD5 (PDF) . Archivo de impresión electrónica de criptología (informe técnico). IACR .
  43. ^ Stevens, Marc ; Bursztein, Elie ; Karpman, Pierre; Albertini, Ange; Markov, Yarik. La primera colisión para SHA-1 completo (PDF) (Informe técnico). Investigación de Google .
    • Marc Stevens; Elie Bursztein; Pierre Karpman; Ange Albertini; Yarik Markov; Alex Petit Bianco; Clement Baisse (23 de febrero de 2017). "Anuncio de la primera colisión SHA1". Blog de seguridad de Google .
  44. ^ Sin truncamiento, se conoce el estado interno completo de la función hash, independientemente de la resistencia a la colisión. Si se trunca la salida, se debe buscar y encontrar la parte eliminada del estado antes de que se pueda reanudar la función hash, lo que permite que continúe el ataque.
  45. ^ "La familia de funciones de la esponja de Keccak" . Consultado el 27 de enero de 2016 .
  46. ^ SUPERCOP Benchmarks Medidas de funciones hash, indexadas por máquina
  47. ^ "SUPERCOP". Archivado desde el original el 15 de febrero de 2015 . Consultado el 24 de febrero de 2015 .
  48. ^ "Conjuntos de cifrados SSL/TLS compatibles". Archivado desde el original el 12 de mayo de 2019. Consultado el 19 de octubre de 2019 .
  49. ^ "Registro de cambios de Mbed TLS, 7 de julio de 2007". GitHub . Archivado desde el original el 4 de febrero de 2019 . Consultado el 19 de octubre de 2019 .
  50. ^ "Manual de referencia técnica del procesador ARM Cortex-A53 MPCore: extensión criptográfica". Archivado desde el original el 2020-06-01 . Consultado el 2022-02-15 .
  51. ^ Principios de funcionamiento de IBM z/Architecture, número de publicación SA22-7832. Consulte las instrucciones KIMD y KLMD en el Capítulo 7.

Lectura adicional

Enlaces externos