Red Hopfield

Forma de red neuronal artificial.

Una red de Hopfield ( memoria asociativa o modelo de Ising-Lenz-Little o red Nakano-Amari-Hopfield ) es un sistema de vidrio giratorio utilizado para modelar redes neuronales , basado en el trabajo de Ernst Ising con Wilhelm Lenz sobre el modelo de Ising de materiales magnéticos. ^[1] Las redes de Hopfield fueron descritas por primera vez con respecto a las redes neuronales recurrentes de forma independiente por Kaoru Nakano en 1971 ^{[2] [3]} y Shun'ichi Amari en 1972, ^{[4] [5]} y con respecto a las redes neuronales biológicas por William Little. en 1974, ^[6] y fueron popularizadas por John Hopfield en 1982. ^[7] Las redes Hopfield sirven como sistemas de memoria direccionables por contenido ("asociativos") con nodos de umbral binarios o con variables continuas. ^[8] Las redes de Hopfield también proporcionan un modelo para comprender la memoria humana. ^{[9] [10]}

Historia

El modelo de Ising en sí fue publicado en la década de 1920 como modelo de magnetismo, sin embargo, estudió el equilibrio térmico, que no cambia con el tiempo. Glauber en 1963 estudió el modelo de Ising evolucionando en el tiempo, como un proceso hacia el equilibrio térmico ( dinámica de Glauber ), añadiendo la componente de tiempo. ^[11]

El segundo componente que se añadió fue la adaptación al estímulo. Shun'ichi Amari en 1972 propuso modificar los pesos de un modelo de Ising mediante la regla de aprendizaje de Hebbian como modelo de memoria asociativa. ^[4] La misma idea fue publicada por William A. Little  [de] en 1974, ^[6] quien fue reconocido por Hopfield en su artículo de 1982. El modelo Sherrington-Kirkpatrick de spin glass, publicado en 1975, es la red Hopfield con inicialización aleatoria. Sherrington y Kirkpatrick descubrieron que es muy probable que la función energética del modelo SK tenga muchos mínimos locales. ^[7]

Hopfield desarrolló redes con dinámica continua en su artículo de 1984. ^[8] Krotov y Hopfield desarrollaron un avance importante en la capacidad de almacenamiento de memoria en 2016 ^[12] a través de un cambio en la dinámica de la red y la función energética. Esta idea fue ampliada por Demircigil y sus colaboradores en 2017. ^[13] La dinámica continua de los modelos de gran capacidad de memoria se desarrolló en una serie de artículos entre 2016 y 2020. ^{[12] [14] [15]}  Gran capacidad de almacenamiento de memoria Hopfield Networks Ahora se denominan Memorias Asociativas Densas o modernas redes de Hopfield .

Estructura

Una red Hopfield con cuatro unidades.

Las unidades en las redes Hopfield son unidades de umbral binario, es decir, las unidades solo toman dos valores diferentes para sus estados, y el valor se determina en función de si la entrada de la unidad excede o no su umbral . Las redes de Hopfield discretas describen las relaciones entre neuronas binarias (que se activan o no) . ^[7] En un momento determinado, el estado de la red neuronal se describe mediante un vector , que registra qué neuronas se activan en una palabra binaria de bits. ${\displaystyle U_{i}}$ ${\displaystyle 1,2,\ldots ,i,j,\ldots ,N}$ ${\displaystyle V}$ ${\displaystyle N}$

Las interacciones entre neuronas tienen unidades que normalmente toman valores de 1 o −1, y esta convención se utilizará a lo largo de este artículo. Sin embargo, otra literatura podría usar unidades que tomen valores de 0 y 1. Estas interacciones se "aprenden" mediante la ley de asociación de Hebb , de modo que, para un cierto estado y nodos distintos ${\displaystyle w_{ij}}$ ${\displaystyle V^{s}}$ ${\displaystyle i,j}$

${\displaystyle w_{ij}=V_{i}^{s}V_{j}^{s}}$

pero . ${\displaystyle w_{ii}=0}$

(Tenga en cuenta que la regla de aprendizaje hebbiana toma la forma cuando las unidades asumen valores en .) ${\displaystyle w_{ij}=(2V_{i}^{s}-1)(2V_{j}^{s}-1)}$ ${\displaystyle \{0,1\}}$

Una vez que la red esté entrenada, ya no evolucione. Si se introduce un nuevo estado de neuronas en la red neuronal, la red actúa sobre las neuronas de tal manera que ${\displaystyle w_{ij}}$ ${\displaystyle V^{s'}}$

• ${\displaystyle V_{i}^{s'}\rightarrow 1}$si ${\displaystyle \sum _{j}w_{ij}V_{j}^{s'}>U_{i}}$
• ${\displaystyle V_{i}^{s'}\rightarrow -1}$si ${\displaystyle \sum _{j}w_{ij}V_{j}^{s'}<U_{i}}$

¿Dónde está el valor umbral de la i-ésima neurona (a menudo se considera 0)? ^[16] De esta manera, las redes de Hopfield tienen la capacidad de "recordar" estados almacenados en la matriz de interacción, porque si un nuevo estado es sometido a la matriz de interacción, cada neurona cambiará hasta coincidir con el estado original (ver la sección Actualizaciones abajo). ${\displaystyle U_{i}}$ ${\displaystyle V^{s'}}$ ${\displaystyle V^{s}}$

Las conexiones en una red Hopfield suelen tener las siguientes restricciones:

• ${\displaystyle w_{ii}=0,\forall i}$(ninguna unidad tiene conexión consigo misma)
• ${\displaystyle w_{ij}=w_{ji},\forall i,j}$(las conexiones son simétricas)

La restricción de que los pesos sean simétricos garantiza que la función de energía disminuya monótonamente mientras se siguen las reglas de activación. ^[17] Una red con pesos asimétricos puede exhibir algún comportamiento periódico o caótico; sin embargo, Hopfield descubrió que este comportamiento se limita a partes relativamente pequeñas del espacio de fase y no afecta la capacidad de la red para actuar como un sistema de memoria asociativa direccionable por contenido.

Hopfield también modeló redes neuronales para valores continuos, en las que la salida eléctrica de cada neurona no es binaria sino un valor entre 0 y 1. ^[8] Descubrió que este tipo de red también era capaz de almacenar y reproducir estados memorizados.

Observe que cada par de unidades i y j en una red Hopfield tiene una conexión que se describe mediante el peso de conectividad . En este sentido, la red de Hopfield puede describirse formalmente como un grafo completo no dirigido , donde es un conjunto de neuronas de McCulloch-Pitts y es una función que vincula pares de unidades a un valor real, el peso de conectividad. ${\displaystyle w_{ij}}$ ${\displaystyle G=\langle V,f\rangle }$ ${\displaystyle V}$ ${\displaystyle f:V^{2}\rightarrow \mathbb {R} }$

Actualizando

La actualización de una unidad (nodo en el gráfico que simula la neurona artificial) en la red Hopfield se realiza mediante la siguiente regla:

${\displaystyle s_{i}\leftarrow \left\{{\begin{array}{ll}+1&{\text{if }}\sum _{j}{w_{ij}s_{j}}\geq \theta _{i},\\-1&{\text{otherwise.}}\end{array}}\right.}$

dónde:

• ${\displaystyle w_{ij}}$es la fuerza del peso de la conexión desde la unidad j a la unidad i (el peso de la conexión).
• ${\displaystyle s_{i}}$es el estado de la unidad i.
• ${\displaystyle \theta _{i}}$es el umbral de la unidad i.

Las actualizaciones en la red Hopfield se pueden realizar de dos formas diferentes:

• Asíncrono : solo se actualiza una unidad a la vez. Esta unidad se puede elegir al azar o se puede imponer un orden predefinido desde el principio.
• Síncrono : todas las unidades se actualizan al mismo tiempo. Esto requiere un reloj central para el sistema para mantener la sincronización. Algunos consideran que este método es menos realista, ya que se basa en la ausencia de un reloj global observado que influya en sistemas biológicos o físicos análogos de interés.

Las neuronas "se atraen o se repelen" en el espacio de estados

El peso entre dos unidades tiene un poderoso impacto sobre los valores de las neuronas. Considere el peso de la conexión entre dos neuronas i y j. Si , la regla de actualización implica que: ${\displaystyle w_{ij}}$ ${\displaystyle w_{ij}>0}$

• cuando , la contribución de j en la suma ponderada es positiva. Por lo tanto, es atraído por j hacia su valor ${\displaystyle s_{j}=1}$ ${\displaystyle s_{i}}$ ${\displaystyle s_{i}=1}$
• cuando , la contribución de j en la suma ponderada es negativa. Por otra parte, es empujado por j hacia su valor ${\displaystyle s_{j}=-1}$ ${\displaystyle s_{i}}$ ${\displaystyle s_{i}=-1}$

Por tanto, los valores de las neuronas i y j convergerán si el peso entre ellas es positivo. De manera similar, divergirán si el peso es negativo.

Principios de funcionamiento de las redes Hopfield discretas y continuas.

Bruck arrojó luz sobre el comportamiento de una neurona en la red discreta de Hopfield al demostrar su convergencia en su artículo de 1990. ^[18]   Un artículo posterior ^[19] investigó más a fondo el comportamiento de cualquier neurona en Hopfield tanto en tiempo discreto como en tiempo continuo. redes cuando la función energética correspondiente se minimiza durante un proceso de optimización. Bruck muestra ^[18] que la neurona j cambia su estado si y sólo si disminuye aún más el siguiente pseudocorte sesgado. La red de Hopfield discreta minimiza el siguiente pseudocorte sesgado ^[19] para la matriz de peso sináptico de la red de Hopfield.

${\displaystyle J_{pseudo-cut}(k)=\sum _{i\in C_{1}(k)}\sum _{j\in C_{2}(k)}w_{ij}+\sum _{j\in C_{1}(k)}{\theta _{j}}}$

donde y representa el conjunto de neuronas que son −1 y +1, respectivamente, en el momento . Para obtener más detalles, consulte el artículo reciente. ^[19] ${\displaystyle C_{1}(k)}$ ${\displaystyle C_{2}(k)}$ ${\displaystyle k}$

La red Hopfield en tiempo discreto siempre minimiza exactamente el siguiente pseudocorte ^{[18] [19]}

${\displaystyle U(k)=\sum _{i=1}^{N}\sum _{j=1}^{N}w_{ij}(s_{i}(k)-s_{j}(k))^{2}+2\sum _{j=1}^{N}\theta _{j}s_{j}(k)}$

La red Hopfield de tiempo continuo siempre minimiza un límite superior para el siguiente corte ponderado ^[19]

${\displaystyle V(t)=\sum _{i=1}^{N}\sum _{j=1}^{N}w_{ij}(f(s_{i}(t))-f(s_{j}(t))^{2}+2\sum _{j=1}^{N}\theta _{j}f(s_{j}(t))}$

donde es una función sigmoidea centrada en cero. ${\displaystyle f(\cdot )}$

La compleja red de Hopfield, por otro lado, generalmente tiende a minimizar el llamado corte de sombra de la compleja matriz de peso de la red. ^[20]

Energía

Panorama energético de una red Hopfield, destacando el estado actual de la red (cuesta arriba), un estado atractor al que eventualmente convergerá, un nivel mínimo de energía y una cuenca de atracción sombreada en verde. Tenga en cuenta que la actualización de Hopfield Network siempre falla en Energía.

Las redes de Hopfield tienen un valor escalar asociado con cada estado de la red, denominado "energía", E , de la red, donde:

${\displaystyle E=-{\frac {1}{2}}\sum _{i,j}w_{ij}s_{i}s_{j}-\sum _{i}\theta _{i}s_{i}}$

Esta cantidad se llama "energía" porque disminuye o permanece igual cuando se actualizan las unidades de la red. Además, bajo actualizaciones repetidas, la red eventualmente convergerá a un estado que es un mínimo local en la función de energía (que se considera una función de Lyapunov ). ^[7] Por lo tanto, si un estado es un mínimo local en la función de energía, es un estado estable para la red. Nótese que esta función energética pertenece a una clase general de modelos en física bajo el nombre de modelos de Ising ; éstos a su vez son un caso especial de redes de Markov , ya que la medida de probabilidad asociada , la medida de Gibbs , tiene la propiedad de Markov .

Red Hopfield en optimización

Hopfield y Tank presentaron la aplicación de la red Hopfield para resolver el clásico problema del viajante en 1985. ^[21] Desde entonces, la red Hopfield se ha utilizado ampliamente para la optimización. La idea de utilizar la red de Hopfield en problemas de optimización es sencilla: si una función de costo restringida/no restringida se puede escribir en la forma de la función de energía E de Hopfield, entonces existe una red de Hopfield cuyos puntos de equilibrio representan soluciones a la optimización restringida/no restringida. problema. Minimizar la función de energía de Hopfield minimiza la función objetivo y satisface las restricciones también, ya que las restricciones están "incrustadas" en los pesos sinápticos de la red. Aunque incluir las restricciones de optimización en los pesos sinápticos de la mejor manera posible es una tarea desafiante, muchos problemas de optimización difíciles con restricciones en diferentes disciplinas se han convertido a la función de energía de Hopfield: sistemas de memoria asociativa, conversión de analógico a digital, problema de programación de tiendas, asignación cuadrática y otros problemas NP-completos relacionados, problema de asignación de canales en redes inalámbricas, problema de enrutamiento de redes móviles ad-hoc, restauración de imágenes, identificación de sistemas, optimización combinatoria, etc., solo por nombrar algunos. Se pueden encontrar más detalles, por ejemplo, en el artículo. ^[19]

Inicialización y ejecución

La inicialización de las redes Hopfield se realiza estableciendo los valores de las unidades en el patrón de inicio deseado. Luego se realizan actualizaciones repetidas hasta que la red converge a un patrón atractor. La convergencia generalmente está asegurada, ya que Hopfield demostró que los atractores de este sistema dinámico no lineal son estables, no periódicos ni caóticos como en otros sistemas ^{[ cita requerida ]} . Por lo tanto, en el contexto de las redes de Hopfield, un patrón atractor es un estado estable final, un patrón que no puede cambiar ningún valor dentro de él al actualizarse ^{[ cita necesaria ]} .

Capacitación

Entrenar una red Hopfield implica reducir la energía de los estados que la red debería "recordar". Esto permite que la red sirva como un sistema de memoria direccionable de contenido, es decir, la red convergerá a un estado "recordado" si se le proporciona sólo una parte del estado. La red se puede utilizar para recuperarse de una entrada distorsionada al estado entrenado que sea más similar a esa entrada. A esto se le llama memoria asociativa porque recupera recuerdos en base a la similitud. Por ejemplo, si entrenamos una red de Hopfield con cinco unidades para que el estado (1, −1, 1, −1, 1) sea un mínimo de energía y le damos a la red el estado (1, −1, −1, −1, 1) convergerá a (1, −1, 1, −1, 1). Por lo tanto, la red está adecuadamente entrenada cuando la energía de los estados que la red debe recordar son mínimos locales. Tenga en cuenta que, a diferencia del entrenamiento con Perceptrón , los umbrales de las neuronas nunca se actualizan.

Reglas de aprendizaje

Existen varias reglas de aprendizaje diferentes que se pueden utilizar para almacenar información en la memoria de la red Hopfield. Es deseable que una regla de aprendizaje tenga las dos propiedades siguientes:

• Local : una regla de aprendizaje es local si cada peso se actualiza utilizando la información disponible para las neuronas en ambos lados de la conexión asociada con ese peso en particular.
• Incremental : se pueden aprender nuevos patrones sin utilizar información de los patrones antiguos que también se han utilizado para el entrenamiento. Es decir, cuando se utiliza un nuevo patrón para el entrenamiento, los nuevos valores de los pesos sólo dependen de los valores antiguos y del nuevo patrón. ^[22]

Estas propiedades son deseables, ya que una regla de aprendizaje que las satisfaga es biológicamente más plausible. Por ejemplo, dado que el cerebro humano siempre está aprendiendo nuevos conceptos, se puede razonar que el aprendizaje humano es incremental. Un sistema de aprendizaje que no fuera incremental generalmente se entrenaría solo una vez, con una gran cantidad de datos de entrenamiento.

Regla de aprendizaje de Hebbian para redes Hopfield

La teoría de Hebb fue introducida por Donald Hebb en 1949 para explicar el "aprendizaje asociativo", en el que la activación simultánea de células neuronales conduce a aumentos pronunciados en la fuerza sináptica entre esas células. ^[23] A menudo se resume como "Las neuronas que se activan juntas se conectan entre sí. Las neuronas que se activan fuera de sincronización no se conectan".

La regla hebbiana es a la vez local e incremental. Para las redes Hopfield, se implementa de la siguiente manera al aprender patrones binarios: ${\displaystyle n}$

${\displaystyle w_{ij}={\frac {1}{n}}\sum _{\mu =1}^{n}\epsilon _{i}^{\mu }\epsilon _{j}^{\mu }}$

donde representa el bit i del patrón . ${\displaystyle \epsilon _{i}^{\mu }}$ ${\displaystyle \mu }$

Si los bits correspondientes a las neuronas i y j tienen el mismo patrón , entonces el producto será positivo. Esto, a su vez, tendría un efecto positivo sobre el peso y los valores de i y j tenderán a igualarse. Sucede lo contrario si los bits correspondientes a las neuronas i y j son diferentes. ${\displaystyle \mu }$ ${\displaystyle \epsilon _{i}^{\mu }\epsilon _{j}^{\mu }}$ ${\displaystyle w_{ij}}$

Regla de aprendizaje de Stokey

Esta regla fue introducida por Amos Storkey en 1997 y es tanto local como incremental. Storkey también demostró que una red de Hopfield entrenada con esta regla tiene una mayor capacidad que una red correspondiente entrenada con la regla de Hebbian. ^[24] Se dice que la matriz de pesos de una red neuronal atractora ^{[ se necesita aclaración ]} sigue la regla de aprendizaje de Storkey si obedece:

${\displaystyle w_{ij}^{\nu }=w_{ij}^{\nu -1}+{\frac {1}{n}}\epsilon _{i}^{\nu }\epsilon _{j}^{\nu }-{\frac {1}{n}}\epsilon _{i}^{\nu }h_{ji}^{\nu }-{\frac {1}{n}}\epsilon _{j}^{\nu }h_{ij}^{\nu }}$

donde es una forma de campo local ^[22] en la neurona i. ${\displaystyle h_{ij}^{\nu }=\sum _{k=1~:~i\neq k\neq j}^{n}w_{ik}^{\nu -1}\epsilon _{k}^{\nu }}$

Esta regla de aprendizaje es local, ya que las sinapsis sólo tienen en cuenta las neuronas que se encuentran a sus lados. La regla utiliza más información de los patrones y pesos que la regla hebbiana generalizada, debido al efecto del campo local.

Patrones espurios

Los patrones que la red utiliza para el entrenamiento (llamados estados de recuperación ) se convierten en atractores del sistema. Las actualizaciones repetidas eventualmente conducirían a la convergencia a uno de los estados de recuperación. Sin embargo, a veces la red convergerá en patrones espurios (diferentes de los patrones de entrenamiento). ^[25] La energía en estos patrones espurios también es un mínimo local. Para cada patrón x almacenado, la negación -x también es un patrón espurio.

Un estado espurio también puede ser una combinación lineal de un número impar de estados de recuperación. Por ejemplo, cuando se utilizan 3 patrones , se puede obtener el siguiente estado espurio: ${\displaystyle \mu _{1},\mu _{2},\mu _{3}}$

${\displaystyle \epsilon _{i}^{\rm {mix}}=\pm \operatorname {sgn}(\pm \epsilon _{i}^{\mu _{1}}\pm \epsilon _{i}^{\mu _{2}}\pm \epsilon _{i}^{\mu _{3}})}$

Los patrones espurios que tienen un número par de estados no pueden existir, ya que podrían sumar cero ^[25]

Capacidad

La capacidad de la red del modelo de red Hopfield está determinada por la cantidad de neuronas y las conexiones dentro de una red determinada. Por tanto, la cantidad de recuerdos que se pueden almacenar depende de las neuronas y las conexiones. Además, se demostró que la precisión de recuperación entre vectores y nodos era de 0,138 (aproximadamente 138 vectores se pueden recuperar del almacenamiento por cada 1000 nodos) (Hertz et al., 1991). Por lo tanto, es evidente que se producirán muchos errores si se intenta almacenar una gran cantidad de vectores. Cuando el modelo de Hopfield no recuerda el patrón correcto, es posible que se haya producido una intrusión, ya que los elementos relacionados semánticamente tienden a confundir al individuo y se produce el recuerdo del patrón incorrecto. Por lo tanto, se ha demostrado que el modelo de red de Hopfield confunde un elemento almacenado con el de otro al recuperarlo. Se pueden cargar en la red recuperaciones perfectas y alta capacidad, >0,14, mediante el método de aprendizaje Storkey; ETAM, ^{[26] [27]} Experimentos ETAM también en. ^[28] Posteriormente se idearon modelos posteriores inspirados en la red Hopfield para aumentar el límite de almacenamiento y reducir la tasa de error de recuperación, y algunos eran capaces de aprender de una sola vez . ^[29]

La capacidad de almacenamiento se puede dar como dónde está el número de neuronas en la red. ${\displaystyle C\cong {\frac {n}{2\log _{2}n}}}$ ${\displaystyle n}$

memoria humana

El modelo de Hopfield explica la memoria asociativa mediante la incorporación de vectores de memoria. Los vectores de memoria se pueden utilizar ligeramente, lo que provocaría la recuperación del vector más similar en la red. Sin embargo, descubriremos que debido a este proceso pueden producirse intrusiones. En la memoria asociativa de la red Hopfield, existen dos tipos de operaciones: autoasociación y heteroasociación. El primero es cuando un vector está asociado consigo mismo y el segundo cuando dos vectores diferentes están asociados en el almacenamiento. Además, ambos tipos de operaciones son posibles de almacenar dentro de una única matriz de memoria, pero sólo si esa matriz de representación dada no es una u otra de las operaciones, sino más bien la combinación (autoasociativa y heteroasociativa) de las dos.

El modelo de red de Hopfield utiliza la misma regla de aprendizaje que la regla de aprendizaje de Hebb (1949) , que caracterizaba el aprendizaje como resultado del fortalecimiento de los pesos en casos de actividad neuronal.

Rizzuto y Kahana (2001) pudieron demostrar que el modelo de red neuronal puede tener en cuenta la repetición en la precisión del recuerdo incorporando un algoritmo de aprendizaje probabilístico. Durante el proceso de recuperación no se produce ningún aprendizaje. Como resultado, los pesos de la red permanecen fijos, lo que demuestra que el modelo puede pasar de una etapa de aprendizaje a una etapa de recuperación. Al agregar una deriva contextual, pudieron mostrar el rápido olvido que ocurre en un modelo de Hopfield durante una tarea de recuerdo con señales. Toda la red contribuye al cambio en la activación de cualquier nodo.

La regla dinámica de McCulloch y Pitts (1943), que describe el comportamiento de las neuronas, lo hace de una manera que muestra cómo las activaciones de múltiples neuronas se corresponden con la activación de la velocidad de activación de una nueva neurona, y cómo los pesos de las neuronas fortalecen la velocidad de activación de una nueva neurona. conexiones sinápticas entre la nueva neurona activada (y las que la activaron). Hopfield usaría la regla dinámica de McCulloch-Pitts para mostrar cómo es posible la recuperación en la red de Hopfield. Sin embargo, Hopfield lo haría de forma repetitiva. Hopfield usaría una función de activación no lineal, en lugar de una función lineal. Por lo tanto, esto crearía la regla dinámica de Hopfield y con esto, Hopfield pudo demostrar que con la función de activación no lineal, la regla dinámica siempre modificará los valores del vector de estado en la dirección de uno de los patrones almacenados.

Memoria asociativa densa o red Hopfield moderna

Las redes de Hopfield ^{[7] [8]} son ​​redes neuronales recurrentes con trayectorias dinámicas que convergen a estados de atractor de punto fijo y se describen mediante una función de energía. El estado de cada neurona modelo está definido por una variable dependiente del tiempo , que puede elegirse como discreta o continua. Un modelo completo describe las matemáticas de cómo el estado futuro de actividad de cada neurona depende de la actividad presente o anterior conocida de todas las neuronas. ${\textstyle i}$ ${\displaystyle V_{i}}$

En el modelo original de memoria asociativa de Hopfield, ^[7] las variables eran binarias y la dinámica se describía mediante una actualización del estado de las neuronas una a la vez. Se definió una función energética cuadrática y la dinámica consistía en cambiar la actividad de cada neurona solo si al hacerlo se reducía la energía total del sistema. Esta misma idea se extendió al caso de ser una variable continua que representa la salida de una neurona y ser una función monótona de una corriente de entrada. La dinámica quedó expresada como un conjunto de ecuaciones diferenciales de primer orden para las cuales la "energía" del sistema siempre disminuía. ^[8]   La energía en el caso continuo tiene un término que es cuadrático en (como en el modelo binario) y un segundo término que depende de la función de ganancia (función de activación de la neurona). Si bien tienen muchas propiedades deseables de la memoria asociativa, ambos sistemas clásicos adolecen de una pequeña capacidad de almacenamiento de memoria, que aumenta linealmente con el número de características de entrada. ^[7] Por el contrario, al aumentar el número de parámetros en el modelo de modo que no haya solo interacciones por pares sino también de orden superior entre las neuronas, se puede aumentar la capacidad de almacenamiento de memoria. ^{[30] [31]} ${\displaystyle V_{i}}$ ${\displaystyle i}$ ${\displaystyle V_{i}}$ ${\displaystyle i}$ ${\displaystyle V_{i}}$ ${\displaystyle V_{i}}$

Las memorias asociativas densas ^[12] (también conocidas como redes de Hopfield modernas ^[14] ) son generalizaciones de las redes de Hopfield clásicas que rompen la relación de escala lineal entre el número de características de entrada y el número de recuerdos almacenados. Esto se logra mediante la introducción de no linealidades más fuertes (ya sea en la función de energía o en las funciones de activación de las neuronas) que conducen a una capacidad de almacenamiento de memoria superlineal ^[12] (incluso exponencial ^[13] ) en función del número de neuronas características. de hecho, aumenta el orden de las interacciones entre las neuronas. ^{[30] [31]} La red todavía requiere un número suficiente de neuronas ocultas. ^[15]

La idea teórica clave detrás de las redes densas de memoria asociativa es utilizar una función de energía y una regla de actualización que tiene un pico más agudo alrededor de los recuerdos almacenados en el espacio de las configuraciones de las neuronas en comparación con el modelo clásico, ^[12] como se demostró cuando el orden superior Las interacciones y los paisajes energéticos posteriores se modelan explícitamente. ^[31]

variables discretas

Un ejemplo simple ^[12] de la red Hopfield moderna se puede escribir en términos de variables binarias que representan el estado activo e inactivo de la neurona modelo . En esta fórmula, los pesos representan la matriz de vectores de memoria (el índice enumera diferentes recuerdos y el índice enumera el contenido de cada memoria correspondiente a la -ésima neurona característica), y la función es una función no lineal de rápido crecimiento. La regla de actualización para neuronas individuales (en el caso asíncrono) se puede escribir de la siguiente forma, que establece que para calcular el estado actualizado de la -ésima neurona, la red compara dos energías: la energía de la red con la -ésima neurona en el estado ON y la energía de la red con la -ésima neurona en el estado OFF, dados los estados de la neurona restante. El estado actualizado de la -ésima neurona selecciona el estado que tiene la más baja de las dos energías. ^[12] ${\displaystyle V_{i}}$ ${\displaystyle V_{i}=+1}$ ${\displaystyle V_{i}=-1}$ ${\displaystyle i}$ $${\displaystyle E=-\sum \limits _{\mu =1}^{N_{\text{mem}}}F{\Big (}\sum \limits _{i=1}^{N_{f}}\xi _{\mu i}V_{i}{\Big )}}$$ ${\textstyle \xi _{\mu i}}$ ${\displaystyle \mu =1...N_{\text{mem}}}$ ${\displaystyle i=1...N_{f}}$ ${\displaystyle i}$ ${\displaystyle F(x)}$ $${\displaystyle V_{i}^{(t+1)}=Sign{\bigg [}\sum \limits _{\mu =1}^{N_{\text{mem}}}{\bigg (}F{\Big (}\xi _{\mu i}+\sum \limits _{j\neq i}\xi _{\mu j}V_{j}^{(t)}{\Big )}-F{\Big (}-\xi _{\mu i}+\sum \limits _{j\neq i}\xi _{\mu j}V_{j}^{(t)}{\Big )}{\bigg )}{\bigg ]}}$$ ${\textstyle i}$ ${\displaystyle i}$ ${\displaystyle i}$ ${\displaystyle i}$

En el caso límite cuando la función de energía no lineal es cuadrática, estas ecuaciones se reducen a la función de energía familiar y la regla de actualización para la red de Hopfield binaria clásica. ^[7] ${\displaystyle F(x)=x^{2}}$

La capacidad de almacenamiento de memoria de estas redes se puede calcular para patrones binarios aleatorios. Para la función de energía de potencia, el número máximo de recuerdos que se pueden almacenar y recuperar de esta red sin errores viene dado por ^[12] Para una función de energía exponencial, la capacidad de almacenamiento de memoria es exponencial en el número de neuronas características ^[13] ${\displaystyle F(x)=x^{n}}$ $${\displaystyle N_{\text{mem}}^{max}\approx {\frac {1}{2(2n-3)!!}}{\frac {N_{f}^{n-1}}{\ln(N_{f})}}}$$ ${\textstyle F(x)=e^{x}}$ $${\displaystyle N_{\text{mem}}^{max}\approx 2^{N_{f}/2}}$$

Fig. 1: Un ejemplo de una red Hopfield moderna continua con neuronas características y neuronas de memoria (ocultas) con conexiones sinápticas simétricas entre ellas. ${\textstyle N_{f}=5}$ ${\displaystyle N_{\text{mem}}=11}$

Variables continuas

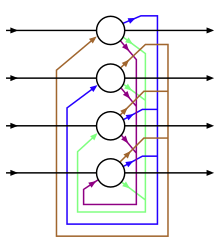
Las redes Hopfield modernas o las memorias asociativas densas se pueden entender mejor en variables continuas y en tiempo continuo. ^{[14] [15]} Considere la arquitectura de la red, que se muestra en la Fig.1, y las ecuaciones para la evolución de los estados de las neuronas ^[15]

donde las corrientes de las neuronas características se indican con y las corrientes de las neuronas de la memoria se indican con ( significa neuronas ocultas). No existen conexiones sinápticas entre las neuronas características o las neuronas de la memoria. Una matriz denota la fuerza de las sinapsis desde una neurona característica hasta la neurona de la memoria . Se supone que las sinapsis son simétricas, de modo que el mismo valor caracteriza una sinapsis física diferente desde la neurona de la memoria hasta la neurona característica . Las salidas de las neuronas de la memoria y las neuronas características se indican con y , que son funciones no lineales de las corrientes correspondientes. En general, estas salidas pueden depender de las corrientes de todas las neuronas de esa capa, de modo que y . Es conveniente definir estas funciones de activación como derivadas de las funciones lagrangianas para los dos grupos de neuronas. ${\textstyle x_{i}}$ ${\displaystyle h_{\mu }}$ ${\displaystyle h}$ ${\displaystyle \xi _{\mu i}}$ ${\displaystyle i}$ ${\displaystyle \mu }$ ${\displaystyle \mu }$ ${\displaystyle i}$ ${\displaystyle f_{\mu }}$ ${\displaystyle g_{i}}$ ${\displaystyle f_{\mu }=f(\{h_{\mu }\})}$ ${\textstyle g_{i}=g(\{x_{i}\})}$

De esta manera la forma específica de las ecuaciones para los estados de las neuronas queda completamente definida una vez especificadas las funciones lagrangianas. Finalmente, las constantes de tiempo para los dos grupos de neuronas se denotan por y , es la corriente de entrada a la red que puede ser impulsada por los datos presentados.  ${\displaystyle \tau _{f}}$ ${\displaystyle \tau _{h}}$ ${\displaystyle I_{i}}$

Fig. 2: Teoría efectiva sobre las neuronas características para varias elecciones comunes de las funciones lagrangianas. El modelo A se reduce a los modelos estudiados en ^{[12] [13]} dependiendo de la elección de la función de activación, el modelo B se reduce al modelo estudiado en ^[14] , el modelo C se reduce al modelo de. ^[15] F es una función " suficientemente suave ". ^[12]

Los sistemas generales de ecuaciones diferenciales no lineales pueden tener muchos comportamientos complicados que pueden depender de la elección de las no linealidades y las condiciones iniciales. Para Hopfield Networks, sin embargo, este no es el caso: las trayectorias dinámicas siempre convergen a un estado de atractor de punto fijo. Esta propiedad se logra porque estas ecuaciones están diseñadas específicamente para que tengan una función de energía subyacente ^[15]

Los términos agrupados entre corchetes representan una transformada de Legendre de la función lagrangiana con respecto a los estados de las neuronas. Si las matrices de Hesse de las funciones lagrangianas son semidefinidas positivas, se garantiza que la función de energía disminuirá en la trayectoria dinámica ^[15]

Esta propiedad permite demostrar que el sistema de ecuaciones dinámicas que describe la evolución temporal de la actividad de las neuronas eventualmente alcanzará un estado de atractor de punto fijo.

En determinadas situaciones, se puede suponer que la dinámica de las neuronas ocultas se equilibra en una escala de tiempo mucho más rápida en comparación con las neuronas características . En este caso, la solución en estado estacionario de la segunda ecuación del sistema ( 1 ) se puede utilizar para expresar las corrientes de las unidades ocultas a través de las salidas de las neuronas características. Esto hace posible reducir la teoría general ( 1 ) a una teoría eficaz únicamente para las neuronas características. Las reglas de actualización efectivas resultantes y las energías para varias elecciones comunes de las funciones lagrangianas se muestran en la Fig.2. En el caso de la función lagrangiana exponencial de suma logarítmica, la regla de actualización (si se aplica una vez) para los estados de las neuronas características es el mecanismo de atención ^[14] comúnmente utilizado en muchos sistemas de IA modernos (ver Ref. ^[15] para la derivación de este resultado de la formulación de tiempo continuo). ${\textstyle \tau _{h}\ll \tau _{f}}$

Relación con la red clásica de Hopfield con variables continuas.

La formulación clásica de redes Hopfield continuas ^[8] puede entenderse ^[15] como un caso límite especial de las redes Hopfield modernas con una capa oculta. Las redes de Hopfield continuas para neuronas con respuesta gradual se describen típicamente ^[8] mediante las ecuaciones dinámicas

y la función de energía

donde , y es la inversa de la función de activación . Este modelo es un límite especial de la clase de modelos que se denomina modelos A, ^[15] con la siguiente elección de las funciones lagrangianas ${\textstyle V_{i}=g(x_{i})}$ ${\displaystyle g^{-1}(z)}$ ${\displaystyle g(x)}$

que, según la definición ( 2 ), conduce a las funciones de activación

Si integramos las neuronas ocultas, el sistema de ecuaciones ( 1 ) se reduce a las ecuaciones de las neuronas características ( 5 ) con , y la expresión general para la energía ( 3 ) se reduce a la energía efectiva. ${\displaystyle T_{ij}=\sum \limits _{\mu =1}^{N_{h}}\xi _{\mu i}\xi _{\mu j}}$

Si bien los dos primeros términos de la ecuación ( 6 ) son iguales a los de la ecuación ( 9 ), los terceros términos parecen superficialmente diferentes. En la ecuación ( 9 ) es una transformada de Legendre del Lagrangiano para las neuronas características, mientras que en ( 6 ) el tercer término es una integral de la función de activación inversa. Sin embargo, estas dos expresiones son equivalentes, ya que las derivadas de una función y su transformada de Legendre son funciones inversas entre sí. La forma más sencilla de ver que estos dos términos son iguales explícitamente es diferenciar cada uno con respecto a . Los resultados de estas diferenciaciones para ambas expresiones son iguales a . Por tanto, las dos expresiones son iguales hasta una constante aditiva. Esto completa la prueba ^[15] de que la red Hopfield clásica con estados continuos ^[8] es un caso límite especial de la red Hopfield moderna ( 1 ) con energía ( 3 ). ${\displaystyle x_{i}}$ ${\displaystyle x_{i}g(x_{i})'}$

Formulación general de la red Hopfield moderna.

Fig. 3: Diagrama de conectividad de la moderna red Hopfield totalmente conectada que consta de cinco neuronas. Los pesos sinápticos se describen mediante una matriz simétrica . ${\displaystyle W_{IJ}}$

Las redes neuronales biológicas tienen un alto grado de heterogeneidad en términos de diferentes tipos de células. Esta sección describe un modelo matemático de una red Hopfield moderna totalmente conectada asumiendo el grado extremo de heterogeneidad: cada neurona es diferente. ^[32] Específicamente, se describe una función de energía y las ecuaciones dinámicas correspondientes suponiendo que cada neurona tiene su propia función de activación y escala de tiempo cinética. Se supone que la red está completamente conectada, de modo que cada neurona está conectada a todas las demás mediante una matriz simétrica de pesos , índices y enumera diferentes neuronas en la red, consulte la figura 3. La forma más sencilla de formular matemáticamente este problema es definir la arquitectura mediante una función lagrangiana que depende de las actividades de todas las neuronas de la red. La función de activación de cada neurona se define como una derivada parcial del lagrangiano con respecto a la actividad de esa neurona. ${\displaystyle W_{IJ}}$ ${\displaystyle I}$ ${\displaystyle J}$ ${\displaystyle L(\{x_{I}\})}$

Desde la perspectiva biológica, se puede considerar como una salida axonal de la neurona . En el caso más simple, cuando el lagrangiano es aditivo para diferentes neuronas, esta definición da como resultado una activación que es una función no lineal de la actividad de esa neurona. Para los lagrangianos no aditivos, esta función de activación puede depender de las actividades de un grupo de neuronas. Por ejemplo, puede contener normalización contrastiva (softmax) o divisiva. Las ecuaciones dinámicas que describen la evolución temporal de una neurona determinada vienen dadas por ^[32] ${\displaystyle g_{I}}$ ${\displaystyle I}$

Esta ecuación pertenece a la clase de modelos llamados modelos de tasa de disparo en neurociencia. Cada neurona recoge las salidas axonales de todas las neuronas, las pondera con los coeficientes sinápticos y produce su propia actividad dependiente del tiempo . La evolución temporal tiene una constante de tiempo , que por lo general puede ser diferente para cada neurona. Esta red tiene una función energética global ^[32] ${\displaystyle I}$ ${\displaystyle g_{J}}$ ${\displaystyle W_{IJ}}$ ${\displaystyle x_{I}}$ ${\displaystyle \tau _{I}}$

donde los dos primeros términos representan la transformada de Legendre de la función lagrangiana con respecto a las corrientes de las neuronas . La derivada temporal de esta función de energía se puede calcular en las trayectorias dinámicas que conducen a (ver ^[32] para más detalles) ${\displaystyle x_{I}}$

El último signo de desigualdad se cumple siempre que la matriz (o su parte simétrica) sea semidefinida positiva. Si, además de esto, la función de energía está acotada desde abajo, se garantiza que las ecuaciones dinámicas no lineales convergerán a un estado de atractor de punto fijo. La ventaja de formular esta red en términos de funciones lagrangianas es que permite experimentar fácilmente con diferentes opciones de funciones de activación y diferentes disposiciones arquitectónicas de las neuronas. Para todas esas elecciones flexibles, las condiciones de convergencia están determinadas por las propiedades de la matriz y la existencia del límite inferior de la función de energía. ${\displaystyle M_{IK}}$ ${\displaystyle M_{IJ}}$

Fig. 4: El diagrama de conectividad de la red de Memoria Asociativa Jerárquica en capas. ^[32] Cada capa puede tener diferente número de neuronas, diferente función de activación y diferentes escalas de tiempo. Los pesos de avance y los pesos de retroalimentación son iguales.

Red de memoria asociativa jerárquica

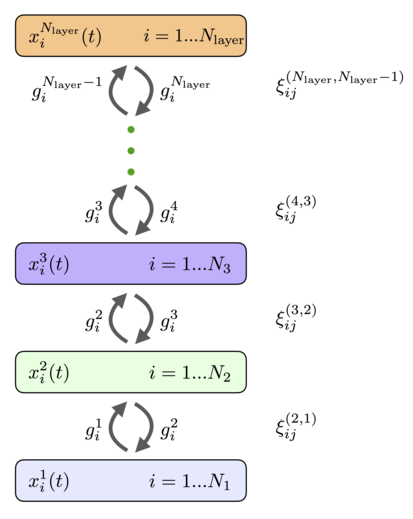
Las neuronas se pueden organizar en capas de modo que cada neurona de una capa determinada tenga la misma función de activación y la misma escala de tiempo dinámica. Si asumimos que no hay conexiones horizontales entre las neuronas dentro de la capa (conexiones laterales) y no hay conexiones de capa de salto, la red general completamente conectada ( 11 ), ( 12 ) se reduce a la arquitectura que se muestra en la Fig.4. Tiene capas de neuronas conectadas de forma recurrente con los estados descritos por variables continuas y las funciones de activación , el índice enumera las capas de la red y el índice enumera las neuronas individuales en esa capa. Las funciones de activación pueden depender de las actividades de todas las neuronas de la capa. Cada capa puede tener un número diferente de neuronas . Estas neuronas están conectadas de forma recurrente con las neuronas de las capas anterior y posterior. Las matrices de pesos que conectan neuronas en capas y se denotan por (el orden de los índices superiores para los pesos es el mismo que el orden de los índices inferiores, en el ejemplo anterior esto significa que el índice enumera las neuronas en la capa y el índice enumera neuronas en la capa ). Los pesos de avance y los pesos de retroalimentación son iguales. Las ecuaciones dinámicas para los estados de las neuronas se pueden escribir como ^[32] ${\displaystyle N_{\text{layer}}}$ ${\displaystyle x_{i}^{A}}$ ${\displaystyle g_{i}^{A}}$ ${\displaystyle A}$ ${\displaystyle i}$ ${\displaystyle N_{A}}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle \xi _{ij}^{(A,B)}}$ ${\displaystyle i}$ ${\displaystyle A}$ ${\displaystyle j}$ ${\displaystyle B}$

con condiciones de contorno

La principal diferencia entre estas ecuaciones y las de las redes de retroalimentación convencionales es la presencia del segundo término, que es responsable de la retroalimentación de las capas superiores. Estas señales de arriba hacia abajo ayudan a las neuronas de las capas inferiores a decidir su respuesta a los estímulos presentados. Siguiendo la receta general es conveniente introducir una función lagrangiana para la -ésima capa oculta, que depende de las actividades de todas las neuronas de esa capa. ^[32] Las funciones de activación en esa capa se pueden definir como derivadas parciales del lagrangiano ${\displaystyle L^{A}(\{x_{i}^{A}\})}$ ${\displaystyle A}$

Con estas definiciones la función de energía (Lyapunov) viene dada por ^[32]

Si las funciones lagrangianas, o equivalentemente las funciones de activación, se eligen de tal manera que las hessianas para cada capa sean semidefinidas positivas y la energía general esté limitada desde abajo, se garantiza que este sistema convergerá a un estado de atractor de punto fijo. La derivada temporal de esta función de energía viene dada por ^[32]

Por lo tanto, la red jerárquica en capas es de hecho una red atractora con la función de energía global. Esta red se describe mediante un conjunto jerárquico de pesos sinápticos que se pueden aprender para cada problema específico.

Ver también

• Memoria asociativa (desambiguación)
• Memoria autoasociativa
• Máquina Boltzmann : como una red Hopfield pero utiliza muestreo de Gibbs recocido en lugar de descenso de gradiente
• Modelo de cognición de sistemas dinámicos.
• modelo ising
• teoría hebbiana

Referencias

1. Pincel, Stephen G. (1967). "Historia del modelo Lenz-Ising". Reseñas de Física Moderna . 39 (4): 883–893. Código bibliográfico : 1967RvMP...39..883B. doi :10.1103/RevModPhys.39.883.
2. Nakano, Kaoru (1971). "Proceso de aprendizaje en un modelo de memoria asociativa". Reconocimiento de patrones y aprendizaje automático : 172–186. doi :10.1007/978-1-4615-7566-5_15. ISBN 978-1-4615-7568-9.
3. Nakano, Kaoru (1972). "Associatron-Un modelo de memoria asociativa". Transacciones IEEE sobre sistemas, hombre y cibernética . SMC-2 (3): 380–388. doi :10.1109/TSMC.1972.4309133.
4. Amari, Shun-Ichi (1972). "Patrones de aprendizaje y secuencias de patrones mediante redes autoorganizadas de elementos de umbral". Transacciones IEEE . C (21): 1197-1206.
5. Schmidhuber, Jürgen (2022). "Historia comentada de la IA moderna y el aprendizaje profundo". arXiv : 2212.11279 [cs.NE].
6. Little, WA (1974). "La existencia de estados persistentes en el cerebro". Biociencias Matemáticas . 19 (1–2): 101–120. doi :10.1016/0025-5564(74)90031-5.
7. Hopfield, JJ (1982). "Redes neuronales y sistemas físicos con habilidades computacionales colectivas emergentes". Procedimientos de la Academia Nacional de Ciencias . 79 (8): 2554–2558. Código bibliográfico : 1982PNAS...79.2554H. doi : 10.1073/pnas.79.8.2554 . PMC 346238 . PMID  6953413. 
8. Hopfield, JJ (1984). "Las neuronas con respuesta graduada tienen propiedades computacionales colectivas como las de las neuronas de dos estados". Procedimientos de la Academia Nacional de Ciencias . 81 (10): 3088–3092. Código bibliográfico : 1984PNAS...81.3088H. doi : 10.1073/pnas.81.10.3088 . PMC 345226 . PMID  6587342. 
9. Amit, DJ (1992). Modelado de la función cerebral: el mundo de las redes neuronales atractoras. Prensa de la Universidad de Cambridge. ISBN 978-0-521-42124-9.
10. Rollos, Edmund T. (2016). Corteza cerebral: principios de funcionamiento. Prensa de la Universidad de Oxford. ISBN 978-0-19-878485-2.
11. Glauber, Roy J. (febrero de 1963). Estadísticas dependientes del tiempo del modelo de Ising "Roy J. Glauber""". Revista de Física Matemática . 4 (2): 294–307. doi : 10.1063/1.1703954 . Consultado el 21 de marzo de 2021 .
12. Krotov, Dmitry; Hopfield, John (2016). "Memoria asociativa densa para el reconocimiento de patrones". Sistemas de procesamiento de información neuronal . 29 : 1172-1180. arXiv : 1606.01164 .
13. Mete, Demircigil; et al. (2017). "Sobre un modelo de memoria asociativa con enorme capacidad de almacenamiento". Revista de Física Estadística . 168 (2): 288–299. arXiv : 1702.01929 . Código Bib : 2017JSP...168..288D. doi :10.1007/s10955-017-1806-y. S2CID  119317128.
14. , Hubert; et al. (2021). "Hopfield Networks es todo lo que necesita". Conferencia Internacional sobre Representaciones del Aprendizaje . arXiv : 2008.02217 .
15. Krotov, Dmitry; Hopfield, John (2021). "Gran problema de memoria asociativa en neurobiología y aprendizaje automático". Conferencia Internacional sobre Representaciones del Aprendizaje . arXiv : 2008.06996 .
16. Hopfield, JJ (1982). "Redes neuronales y sistemas físicos con habilidades computacionales colectivas emergentes". Procedimientos de la Academia Nacional de Ciencias . 79 (8): 2554–2558. Código bibliográfico : 1982PNAS...79.2554H. doi : 10.1073/pnas.79.8.2554 . PMC 346238 . PMID  6953413. 
17. MacKay, David JC (2003). "42. Redes Hopfield". Teoría de la información, inferencia y algoritmos de aprendizaje . Prensa de la Universidad de Cambridge . pag. 508.ISBN​ 978-0521642989. Esta prueba de convergencia depende crucialmente del hecho de que las conexiones de la red Hopfield sean simétricas . También depende de que las actualizaciones se realicen de forma asincrónica.
18. Bruck, J. (octubre de 1990). "Sobre las propiedades de convergencia del modelo de Hopfield". Proc. IEEE . 78 (10): 1579–85. doi :10.1109/5.58341.
19. Uykan, Z. (septiembre de 2020). "Sobre el principio de funcionamiento de las redes neuronales de Hopfield y su equivalencia con GADIA en optimización". Transacciones IEEE sobre redes neuronales y sistemas de aprendizaje . 31 (9): 3294–3304. doi :10.1109/TNNLS.2019.2940920. PMID  31603804. S2CID  204331533.
20. Uykan, Z. (marzo de 2021). "Minimización/maximización de cortes de sombras y redes neuronales complejas de Hopfield". Transacciones IEEE sobre redes neuronales y sistemas de aprendizaje . 32 (3): 1096-1109. doi : 10.1109/TNNLS.2020.2980237 . PMID  32310787. S2CID  216047831.
21. Hopfield, JJ; Tanque, DW (1985). "Cálculo neuronal de decisiones en problemas de optimización". Cibernética biológica . 52 (3): 141–6. doi :10.1007/BF00339943. PMID  4027280. S2CID  36483354.
22. Storkey, AJ; Valabregue, R. (1999). "Las cuencas de atracción de una nueva regla de aprendizaje de Hopfield". Redes neuronales . 12 (6): 869–876. CiteSeerX 10.1.1.19.4681 . doi :10.1016/S0893-6080(99)00038-6. PMID  12662662. 
23. Hebb 1949
24. Cigüeña, Amós (1997). "Aumentar la capacidad de una red Hopfield sin sacrificar la funcionalidad". Redes neuronales artificiales - ICANN'97 . Apuntes de conferencias sobre informática. vol. 1327. Saltador. págs. 451–6. CiteSeerX 10.1.1.33.103 . doi :10.1007/BFb0020196. ISBN  978-3-540-69620-9.
25. Hercios 1991
26. Liou, CY; Lin, S.-L. (2006). "Carga de memoria finita en neuronas peludas" (PDF) . Computación Natural . 5 (1): 15–42. doi :10.1007/s11047-004-5490-x. S2CID  35025761.
27. Liou, CY; Yuan, S.-K. (1999). "Memoria asociativa tolerante a errores". Cibernética biológica . 81 (4): 331–342. doi :10.1007/s004220050566. PMID  10541936. S2CID  6168346.
28. Yuan, S.-K. (junio de 1997). Ampliación de cuencas de atracción de la memoria asociativa (tesis de maestría). Universidad Nacional de Taiwán. 991010725609704786.
29. ABOUDIB, Ala; GRIPON, Vicente; JIANG, Xiaoran (2014). "Un estudio de algoritmos de recuperación de mensajes dispersos en redes de camarillas neuronales". COGNITIVE 2014: Sexta Conferencia Internacional sobre Tecnologías y Aplicaciones Cognitivas Avanzadas . págs. 140–6. arXiv : 1308.4506 . Código Bib : 2013arXiv1308.4506A.
30. Horn, D; Usher, M (1988). "Capacidades de modelos de memoria multiconectados". J. Física. Francia . 49 (3): 389–395. doi :10.1051/jphys:01988004903038900.
31. Quemaduras, Thomas; Fukai, Tomoki (2023). "Redes Hopfield simples". Conferencia Internacional sobre Representaciones del Aprendizaje . 11 . arXiv : 2305.05179 .
32. Krotov, Dmitry (2021). "Memoria asociativa jerárquica". arXiv : 2107.06446 [cs.NE].

• Hebb, DO (2005) [1949]. La organización del comportamiento: una teoría neuropsicológica. Prensa de Psicología. ISBN 978-1-135-63190-1.
• Hertz, John A. (2018) [1991]. Introducción a la teoría de la computación neuronal. Prensa CRC. ISBN 978-0-429-96821-1.
• McCulloch, WS; Pitts, WH (1943). "Un cálculo lógico de las ideas inmanentes a la actividad nerviosa". Boletín de Biofísica Matemática . 5 (4): 115-133. doi :10.1007/BF02478259.
• Polin, SM; Kahana, MJ (2008). "Búsqueda de memoria y representación neuronal del contexto". Tendencias en Ciencias Cognitivas . 12 (1): 24–30. doi :10.1016/j.tics.2007.10.010. PMC  2839453 . PMID  18069046.
• Rizzuto, DS; Kahana, MJ (2001). "Un modelo de red neuronal autoasociativa de aprendizaje asociado por pares". Computación neuronal . 13 (9): 2075–2092. CiteSeerX  10.1.1.45.7929 . doi :10.1162/089976601750399317. PMID  11516358. S2CID  7675117.
• Kruse, Rudolf; Borgelt, cristiano; Klawonn, Frank; Moewes, cristiano; Steinbrecher, Matías; Celebrado, Pascal (2013). Inteligencia computacional: una introducción metodológica. Saltador. ISBN 978-1-4471-5013-8.

enlaces externos

• Rojas, Raúl (12 de julio de 1996). "13. El modelo Hopfield" (PDF) . Redes neuronales: una introducción sistemática. Saltador. ISBN 978-3-540-60505-8.
• Javascript de la red Hopfield
• El problema del viajante Archivado el 30 de mayo de 2015 en Wayback Machine - Applet JAVA de red neuronal Hopfield
• Hopfield, John (2007). "Red Hopfield". Scholarpedia . 2 (5): 1977. Código bibliográfico : 2007SchpJ...2.1977H. doi : 10.4249/scholarpedia.1977 .
• Fletcher, Tristán. "Aprendizaje en red Hopfield utilizando variables latentes deterministas" (PDF) (Tutorial). Archivado desde el original (PDF) el 5 de octubre de 2011.