
En matemáticas , un punto de silla o punto minimax [1] es un punto en la superficie del gráfico de una función donde las pendientes (derivadas) en direcciones ortogonales son todas cero (un punto crítico ), pero que no es un extremo local de la función. [2] Un ejemplo de un punto de silla es cuando hay un punto crítico con un mínimo relativo a lo largo de una dirección axial (entre picos) y en un máximo relativo a lo largo del eje de cruce. Sin embargo, un punto de silla no necesita tener esta forma. Por ejemplo, la función tiene un punto crítico en que es un punto de silla ya que no es ni un máximo relativo ni un mínimo relativo, pero no tiene un máximo relativo ni un mínimo relativo en la dirección .

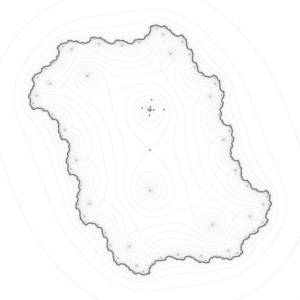
El nombre deriva del hecho de que el ejemplo prototípico en dos dimensiones es una superficie que se curva hacia arriba en una dirección y se curva hacia abajo en una dirección diferente, similar a una silla de montar . En términos de líneas de contorno , un punto de silla en dos dimensiones da lugar a un mapa de contorno con un par de líneas que se cruzan en el punto. Tales intersecciones son raras en los mapas reales de Ordnance Survey, ya que es poco probable que la altura del punto de silla coincida con los múltiplos enteros utilizados en tales mapas. En cambio, el punto de silla aparece como un espacio en blanco en medio de cuatro conjuntos de líneas de contorno que se acercan y se alejan de él. Para un punto de silla básico, estos conjuntos ocurren en pares, con un par alto opuesto y un par bajo opuesto ubicados en direcciones ortogonales. Las líneas de contorno críticas generalmente no tienen que cruzarse ortogonalmente.
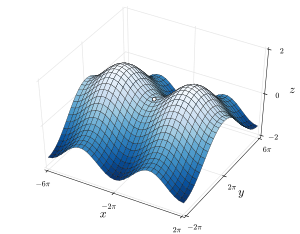
Un criterio simple para verificar si un punto estacionario dado de una función de valores reales F ( x , y ) de dos variables reales es un punto de silla es calcular la matriz hessiana de la función en ese punto: si la matriz hessiana es indefinida , entonces ese punto es un punto de silla. Por ejemplo, la matriz hessiana de la función en el punto estacionario es la matriz
que es indefinida. Por lo tanto, este punto es un punto de silla. Este criterio proporciona solo una condición suficiente. Por ejemplo, el punto es un punto de silla para la función , pero la matriz hessiana de esta función en el origen es la matriz nula , que no es indefinida.
En términos más generales, un punto de silla para una función suave (cuyo gráfico es una curva , superficie o hipersuperficie ) es un punto estacionario tal que la curva/superficie/etc. en la vecindad de ese punto no está completamente en ningún lado del espacio tangente en ese punto.

En un dominio unidimensional, un punto de silla es un punto que es a la vez un punto estacionario y un punto de inflexión . Puesto que es un punto de inflexión, no es un extremo local .


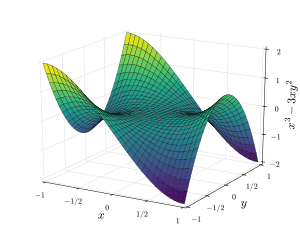
Una superficie de silla de montar es una superficie lisa que contiene uno o más puntos de silla de montar.
Ejemplos clásicos de superficies bidimensionales en forma de silla de montar en el espacio euclidiano son las superficies de segundo orden, el paraboloide hiperbólico (que a menudo se denomina " superficie en forma de silla de montar" o "superficie en forma de silla de montar estándar") y el hiperboloide de una hoja . Las patatas fritas o chips Pringles son un ejemplo cotidiano de una forma de paraboloide hiperbólico.
Las superficies en forma de silla de montar tienen una curvatura gaussiana negativa , lo que las distingue de las superficies convexas/elípticas, que tienen una curvatura gaussiana positiva. Una superficie en forma de silla de montar clásica de tercer orden es la superficie en forma de silla de montar de mono . [3]
En un juego de suma cero para dos jugadores definido en un espacio continuo, el punto de equilibrio es un punto de silla.
Para un sistema autónomo lineal de segundo orden, un punto crítico es un punto de silla si la ecuación característica tiene un valor propio real positivo y uno negativo . [4]
En la optimización sujeta a restricciones de igualdad, las condiciones de primer orden describen un punto de silla del Lagrangiano .
En sistemas dinámicos , si la dinámica está dada por una función diferenciable f , entonces un punto es hiperbólico si y solo si la diferencial de ƒ n (donde n es el período del punto) no tiene valor propio en el círculo unitario (complejo) cuando se calcula en el punto. Entonces, un punto de silla es un punto periódico hiperbólico cuyas variedades estables e inestables tienen una dimensión que no es cero.
Un punto de silla de una matriz es un elemento que es a la vez el elemento más grande de su columna y el elemento más pequeño de su fila.