Punto isoperimétrico

En geometría , el punto isoperimétrico es el centro de un triángulo , un punto especial asociado con un triángulo plano . El término fue introducido originalmente por GR Veldkamp en un artículo publicado en la revista American Mathematical Monthly en 1985 para denotar un punto $P$ en el plano de un triángulo $△ ABC$ que tiene la propiedad de que los triángulos $△ PBC, △ PCA, △ PAB$ tienen isoperímetros, es decir, tienen la propiedad de que ^[1]^[2]

${\begin{aligned}&{\overline {PB}}+{\overline {BC}}+{\overline {CP}},\\=\ &{\overline {PC}}+{\overline {CA}}+{\overline {AP}},\\=\ &{\overline {PA}}+{\overline {AB}}+{\overline {BP}}.\end{aligned}}$

Los puntos isoperimétricos en el sentido de Veldkamp existen sólo para triángulos que satisfacen ciertas condiciones. El punto isoperimétrico de $△ ABC$ en el sentido de Veldkamp, si existe, tiene las siguientes coordenadas trilineales . ^[3]

$\sec {\frac {A}{2}}\cos {\frac {B}{2}}\cos {\frac {C}{2}}-1\ :\ \sec {\frac {B}{2}}\cos {\frac {C}{2}}\cos {\frac {A}{2}}-1\ :\ \sec {\frac {C}{2}}\cos {\frac {A}{2}}\cos {\frac {B}{2}}-1$

Dado cualquier triángulo $△ ABC$ se le puede asociar un punto $P$ que tenga coordenadas trilineales como las dadas arriba. Este punto es un centro de triángulo y en la Enciclopedia de Centros de Triángulos (ETC) de Clark Kimberling se le llama el punto isoperimétrico del triángulo $△$ $ABC$ . Se designa como el centro del triángulo X (175). ^[4] El punto X (175) no necesita ser un punto isoperimétrico del triángulo $△$ $ABC$ en el sentido de Veldkamp. Sin embargo, si existe un punto isoperimétrico del triángulo $△$ $ABC$ en el sentido de Veldkamp, entonces sería idéntico al punto X (175).

El punto $P$ con la propiedad de que los triángulos $△ PBC, △ PCA, △ PAB$ tienen perímetros iguales fue estudiado ya en 1890 en un artículo de Emile Lemoine . ^[4]^[5]

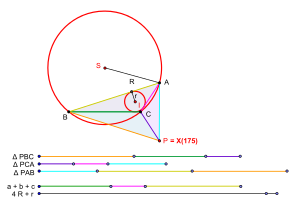
Existencia de un punto isoperimétrico en el sentido de Veldkamp

Sea $△ ABC$ un triángulo cualquiera. Sean las longitudes de los lados de este triángulo $a, b, c$ . Sea su radio circunscrito $R$ y su radio interior $r$ . La condición necesaria y suficiente para la existencia de un punto isoperimétrico en el sentido de Veldkamp puede enunciarse de la siguiente manera. ^[1]

El triángulo

△ ABC

tiene un punto isoperimétrico en el sentido de Veldkamp si y sólo si

a+b+c>4R+r.

Para todos los triángulos acutángulos $△ ABC$ tenemos $a + b + c > 4 R + r$ , y por lo tanto todos los triángulos acutángulos tienen puntos isoperimétricos en el sentido de Veldkamp.

Propiedades

Sea $P$ el centro del triángulo X (175) del triángulo $△ ABC$ . ^[4]

$P$ se encuentra en la línea que une el incentro y el punto de Gergonne de $△ ABC$ .
Si $P$ es un punto isoperimétrico de $△ ABC$ en el sentido de Veldkamp, entonces los excírculos de los triángulos $△ PBC, △ PCA, △ PAB$ son tangentes entre sí por pares y $P$ es su centro radical.
Si $P$ es un punto isoperimétrico de $△ ABC$ en el sentido de Veldkamp, entonces los perímetros de $△ PBC, △ PCA, △ PAB$ son iguales a

${\frac {2\triangle }{{\bigl |}4R+r-(a+b+c){\bigr |}}}$ donde $△$ es el área, $R$ es el radio circunscrito, $r$ es el radio interno y $a, b, c$ son las longitudes de los lados de $△ ABC$ . ^[6]

Círculos de barro

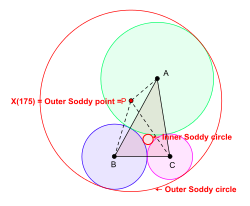
Dado un triángulo $△ ABC$ se pueden dibujar círculos en el plano de $△ ABC$ con centros en $A, B, C$ tales que sean tangentes entre sí externamente. En general, se pueden dibujar dos círculos nuevos tales que cada uno de ellos sea tangente a los tres círculos con $A, B, C$ como centros. (Uno de los círculos puede degenerar en una línea recta). Estos círculos son los círculos de Soddy de $△ ABC$ . El círculo con el radio más pequeño es el círculo de Soddy interior y su centro se llama punto de Soddy interior o centro de Soddy interior de $△ ABC$ . El círculo con el radio más grande es el círculo de Soddy exterior y su centro se llama punto de Soddy exterior o centro de Soddy exterior del triángulo $△ ABC$ . ^[6]^[7]

El centro del triángulo X (175), el punto isoperimétrico en el sentido de Kimberling, es el punto Soddy exterior de $△ ABC$ .

Referencias

^ ab GR Veldkamp (1985). "El punto isoperimétrico y el punto o puntos de desvío igual". Amer. Math. Monthly . 92 (8): 546–558. doi :10.2307/2323159. JSTOR 2323159.
^ Hajja, Mowaffaq; Yff, Peter (2007). "El punto isoperimétrico y el punto o puntos de desvío igual en un triángulo". Journal of Geometry . 87 (1–2): 76–82. doi :10.1007/s00022-007-1906-y. S2CID 122898960.
^ Kimberling, Clark. "Punto isoperimétrico y punto de desvío igual" . Consultado el 27 de mayo de 2012 .
^ abc Kimberling, Clark. «X(175) Punto isoperimétrico». Archivado desde el original el 19 de abril de 2012. Consultado el 27 de mayo de 2012 .
^ El artículo de Emile Lemoine se puede consultar en Gallica. El artículo comienza en la página 111 y el tema se analiza en la página 126. Gallica
^ por Nikolaos Dergiades (2007). "The Soddy Circles" (PDF) . Forum Geometricorum . 7 : 191–197 . Consultado el 29 de mayo de 2012 .
^ "Círculos de barro" . Consultado el 29 de mayo de 2012 .

Enlaces externos

Puntos de desvío isoperimétricos e iguales - ilustración interactiva en Geogebratube