La compuerta óptica resuelta en frecuencia ( FROG ) es un método general para medir la fase espectral de pulsos láser ultracortos , que varían de sub femtosegundos a aproximadamente un nanosegundo de duración. Inventada en 1991 por Rick Trebino y Daniel J. Kane, FROG fue la primera técnica para resolver este problema, que es difícil porque, por lo general, para medir un evento en el tiempo, se requiere un evento más corto con el que medirlo. Por ejemplo, para medir el estallido de una burbuja de jabón se necesita una luz estroboscópica con una duración más corta para congelar la acción. Debido a que los pulsos láser ultracortos son los eventos más cortos jamás creados, antes de FROG, muchos pensaban que su medición completa en el tiempo no era posible. Sin embargo, FROG resolvió el problema midiendo un "autoespectrograma" del pulso, en el que el pulso se compuerta a sí mismo en un medio óptico no lineal y la parte compuerta resultante del pulso se resuelve espectralmente como una función del retraso entre los dos pulsos. La recuperación del pulso de su traza FROG se logra utilizando un algoritmo de recuperación de fase bidimensional.
FROG es actualmente la técnica estándar para medir pulsos láser ultracortos, reemplazando un método más antiguo llamado autocorrelación , que solo brindaba una estimación aproximada de la longitud del pulso. FROG es simplemente una autocorrelación resuelta espectralmente, que permite el uso de un algoritmo de recuperación de fase para recuperar la intensidad del pulso precisa y la fase en función del tiempo. Puede medir pulsos láser ultracortos muy simples y muy complejos, y ha medido el pulso más complejo jamás medido sin el uso de un pulso de referencia. Existen versiones simples de FROG (con el acrónimo GRENOUILLE , la palabra francesa para FROG), que utilizan solo unos pocos componentes ópticos de fácil alineación. Tanto FROG como GRENOUILLE se usan comúnmente en laboratorios de investigación e industriales de todo el mundo.
FROG y la autocorrelación comparten la idea de combinar un pulso consigo mismo en un medio no lineal. Dado que un medio no lineal solo producirá la señal deseada cuando ambos pulsos estén presentes al mismo tiempo (es decir, “puerta óptica”), variar el retardo entre las copias de pulso y medir la señal en cada retardo proporciona una estimación vaga de la longitud del pulso. Los autocorreladores miden un pulso midiendo la intensidad del campo de señal no lineal. Estimar la longitud del pulso requiere suponer una forma de pulso, y la fase del campo eléctrico del pulso no se puede medir en absoluto. FROG extiende esta idea midiendo el espectro de la señal en cada retardo (de ahí que se la llame “resuelta en frecuencia”), en lugar de solo la intensidad. Esta medición crea un espectrograma del pulso, que se puede utilizar para determinar el campo eléctrico complejo como una función del tiempo o la frecuencia siempre que se conozca la no linealidad del medio.
El espectrograma FROG (generalmente llamado traza FROG) es un gráfico de intensidad en función de la frecuencia y el retardo . Sin embargo, el campo de señal de la interacción no lineal es más fácil de expresar en el dominio del tiempo, por lo que la expresión típica para la traza FROG incluye una transformada de Fourier .
El campo de señal no lineal depende del pulso original, , y del proceso no lineal utilizado, que casi siempre se puede expresar como , de modo que . La no linealidad más común es la generación del segundo armónico , donde . La expresión para la traza en términos del campo de pulsos es entonces:
Existen muchas variaciones posibles de esta configuración básica. Si se dispone de un pulso de referencia conocido, se puede utilizar como pulso de activación en lugar de una copia del pulso desconocido. Esto se conoce como FROG de correlación cruzada o XFROG. Además, se pueden utilizar otros efectos no lineales además de la generación del segundo armónico, como la generación del tercer armónico (THG) o la activación de polarización (PG). Estos cambios afectarán la expresión de .
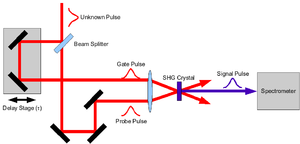
En una configuración FROG de disparos múltiples típica, el pulso desconocido se divide en dos copias con un divisor de haz. Una copia se retrasa una cantidad conocida en relación con la otra. Ambos pulsos se enfocan en el mismo punto en un medio no lineal y el espectro de la señal no lineal se mide con un espectrómetro. Este proceso se repite para muchos puntos de retraso.
Se puede realizar una medición FROG en una sola toma con algunos ajustes menores. Las dos copias de pulso se cruzan en un ángulo y se enfocan en una línea en lugar de en un punto. Esto crea un retraso variable entre los dos pulsos a lo largo del enfoque de la línea. En esta configuración, es común utilizar un espectrómetro casero, que consta de una rejilla de difracción y una cámara, para capturar la medición.
Aunque teóricamente es algo complejo, el método de proyecciones generalizadas ha demostrado ser un método extremadamente confiable para recuperar pulsos de trazas FROG. Desafortunadamente, su sofisticación es fuente de algunos malentendidos y desconfianza por parte de los científicos de la comunidad óptica. Por lo tanto, en esta sección se intentará brindar una idea de la filosofía básica y la implementación del método, aunque no de su funcionamiento detallado.
En primer lugar, imaginemos un espacio que contiene todos los campos eléctricos de señal posibles. Para una medición dada, existe un conjunto de estos campos que satisfarán la traza FROG medida. Nos referimos a estos campos como campos que satisfacen la restricción de datos. Existe otro conjunto que consiste en los campos de señal que se pueden expresar utilizando la forma para la interacción no lineal utilizada en la medición. Para la generación de segundo armónico (SHG), este es el conjunto de campos que se pueden expresar en la forma . Esto se conoce como satisfacer la restricción de forma matemática.
Estos dos conjuntos se intersecan exactamente en un punto. Solo hay un campo de señal posible que tenga la intensidad correcta para coincidir con el trazo de datos y se ajuste a la forma matemática dictada por la interacción no lineal. Para encontrar ese punto, que dará el pulso que estamos tratando de medir, se utilizan proyecciones generalizadas. El algoritmo de proyecciones generalizadas opera en este espacio de campo eléctrico. En cada paso, encontramos el punto más cercano al punto de estimación actual que satisfará la restricción para el otro conjunto. Es decir, la estimación actual se "proyecta" sobre el otro conjunto. Este punto más cercano se convierte en la nueva estimación actual y se encuentra el punto más cercano en el primer conjunto. Al alternar entre proyectar sobre el conjunto de restricciones matemáticas y proyectar sobre el conjunto de restricciones de datos, finalmente llegamos a la solución.
La proyección sobre el conjunto de restricciones de datos es sencilla. Para estar en ese conjunto, la magnitud al cuadrado del campo de señal tiene que coincidir con la intensidad medida por la traza. El campo de señal se transforma en Fourier a . El punto más cercano en el conjunto de restricciones de datos se encuentra reemplazando la magnitud de por la magnitud de los datos, dejando intacta la fase de .
Proyectar sobre el conjunto de restricciones matemáticas no es sencillo. A diferencia de la restricción de datos, no hay una manera fácil de determinar qué punto del conjunto de restricciones matemáticas es el más cercano. Se crea una expresión general para la distancia entre el punto actual y cualquier punto del conjunto de restricciones matemáticas y luego se minimiza esa expresión tomando el gradiente de esa distancia con respecto al valor de campo actual. Este proceso se analiza con más detalle en este artículo.
Este ciclo se repite hasta que el error entre la estimación de la señal y la restricción de datos (después de aplicar la restricción matemática) alcanza un valor mínimo objetivo. se puede encontrar simplemente integrando con respecto al retardo . Por lo general, se construye matemáticamente un segundo trazo FROG a partir de la solución y se compara con la medición original.
Una característica importante de una medición FROG es que se recogen muchos más puntos de datos de los estrictamente necesarios para encontrar el campo eléctrico del pulso. Por ejemplo, digamos que la traza medida consta de 128 puntos en la dirección de retardo y 128 puntos en la dirección de frecuencia. Hay 128 × 128 puntos en total en la traza. Usando estos puntos, se recupera un campo eléctrico que tiene 2 × 128 puntos (128 para la magnitud y otros 128 para la fase). Este es un sistema masivamente sobredeterminado , [1] lo que significa que el número de ecuaciones es mucho mayor que el número de incógnitas. Por lo tanto, la importancia de que cada punto de datos individual sea absolutamente correcto se reduce en gran medida. Esto es muy útil para mediciones del mundo real que pueden verse afectadas por el ruido del detector y los errores sistemáticos. Es extremadamente improbable que el ruido afecte a la traza medida de una manera que pueda confundirse con un fenómeno físico en el pulso. El algoritmo FROG tiende a "ver a través" de estos efectos debido a la cantidad de información adicional disponible y al uso de una restricción de forma matemática para encontrar una solución. Esto significa que el error entre un rastro FROG experimental y un rastro FROG recuperado rara vez es cero, aunque debería ser bastante pequeño para rastros sin errores sistemáticos.
En consecuencia, se deben investigar las diferencias significativas entre los rastros de FROG medidos y recuperados. La configuración experimental puede estar desalineada o puede haber distorsiones espacio-temporales significativas en el pulso. Si la medición promedia varios o muchos pulsos, entonces esos pulsos pueden variar significativamente entre sí.