Problema de apilamiento de bloques

Problema de apilar bloques de manera que se extiendan lo más posible más allá de su base.

Los primeros nueve bloques en la solución del problema de apilamiento de bloques de ancho simple con los voladizos indicados

En estática , el problema de apilamiento de bloques (a veces conocido como La Torre Inclinada de Lire (Johnson 1955), también el problema de apilamiento de libros o una serie de otros términos similares) es un rompecabezas relacionado con el apilamiento de bloques en el borde de una mesa.

Declaración

El problema del apilamiento de bloques es el siguiente:

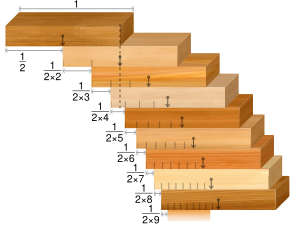
Coloque bloques rectangulares rígidos idénticos en una pila estable sobre el borde de una mesa de tal manera que se maximice el voladizo. ${\displaystyle N}$

Paterson et al. (2007) proporcionan una larga lista de referencias sobre este problema que se remontan a textos de mecánica de mediados del siglo XIX.

Variantes

De ancho simple

El problema de ancho único implica tener solo un bloque en cualquier nivel dado. En el caso ideal de bloques perfectamente rectangulares, la solución al problema de ancho único es que el voladizo máximo está dado por el ancho de un bloque. Esta suma es la mitad de la suma parcial correspondiente de la serie armónica . Debido a que la serie armónica diverge, el voladizo máximo tiende a infinito a medida que aumenta, lo que significa que es posible lograr cualquier voladizo arbitrariamente grande, con bloques suficientes. ${\textstyle \sum _{i=1}^{N}{\frac {1}{2i}}}$ ${\displaystyle N}$

El número de bloques necesarios para alcanzar al menos longitudes de bloque más allá del borde de la tabla es 4, 31, 227, 1674, 12367, 91380, ... (secuencia A014537 en la OEIS ). ^[1] ${\displaystyle N}$

Multi-ancho

Comparación de las soluciones al problema de apilamiento de bloques de ancho simple (arriba) y de ancho múltiple (abajo) con tres bloques

Las pilas de varios anchos que utilizan contrapeso pueden dar voladizos más grandes que una pila de un solo ancho. Incluso para tres bloques, apilar dos bloques contrapesados ​​sobre otro bloque puede dar un voladizo de 1, mientras que el voladizo en el caso ideal simple es como máximo de ⁠11/12⁠ . Como demostraron Paterson et al. (2007), asintóticamente, el voladizo máximo que se puede lograr con pilas de ancho múltiple es proporcional a la raíz cúbica del número de bloques, en contraste con el caso de ancho único en el que el voladizo es proporcional al logaritmo del número de bloques. Sin embargo, se ha demostrado que en realidad esto es imposible y el número de bloques que podemos mover hacia la derecha, debido a la tensión del bloque, no es más que un número especificado. Por ejemplo, para un ladrillo especial con h =0,20 m , módulo de Young E =3000 MPa y densidad ρ =1,8 × 10 ³  kg/m ³ y tensión de compresión límite3 MPa , el valor aproximado de N será 853 y la altura máxima de la torre se convierte en170 metros [ ^2]

Prueba de solución de variante de ancho simple

La fórmula anterior para el voladizo máximo de bloques, cada uno con longitud y masa , apilados uno a un nivel, se puede demostrar por inducción considerando los torques en los bloques sobre el borde de la mesa sobre el que sobresalen. Los bloques se pueden modelar como masas puntuales ubicadas en el centro de cada bloque, asumiendo una densidad de masa uniforme. En el caso base ( ), el centro de masa del bloque se encuentra por encima del borde de la mesa, lo que significa un voladizo de . Para los bloques, el centro de masa del sistema de bloques debe estar por encima del borde de la mesa, y el centro de masa de los bloques superiores debe estar por encima del borde del primero para el equilibrio estático. ^[3] Si el bloque º sobresale del º por y el voladizo del primero es , ^[4] ${\displaystyle n}$ ${\displaystyle l}$ ${\displaystyle m}$ ${\displaystyle n=1}$ ${\displaystyle l/2}$ ${\displaystyle k}$ ${\displaystyle k}$ ${\displaystyle k-1}$ ${\displaystyle k}$ ${\displaystyle (k-1)}$ ${\displaystyle l/2}$ ${\displaystyle x}$

${\displaystyle (k-1)mgx=(l/2-x)mg\implies x=l/2k,}$

donde denota el campo gravitatorio . Si los bloques superiores sobresalen de su centro de masas en , entonces, suponiendo la hipótesis inductiva, el voladizo máximo de la mesa es ${\displaystyle g}$ ${\displaystyle k-1}$ ${\displaystyle y}$

${\displaystyle y+{\frac {l}{2k}}=\sum _{i=1}^{k}{l/2i}\implies y=\sum _{i=1}^{k-1}{l/2i}.}$

Para los bloques, indica cuánto sobresalen los bloques superiores de su centro de masas , y . Entonces, el voladizo máximo sería: ${\displaystyle k+1}$ ${\displaystyle y}$ ${\displaystyle k+1-1}$ ${\displaystyle (y=\sum _{i=1}^{k}l/2i)}$ ${\displaystyle x={\frac {l}{2(k+1)}}}$

${\displaystyle {\frac {l}{2(k+1)}}+\sum _{i=1}^{k}l/2i=\sum _{i=1}^{k+1}l/2i.}$

Método de Mike Paterson para aumentar el voladizo de 16 bloques de ancho unitario y ancho b a 2 √ 1 + b  ² desplazando los bloques perpendicularmente a sus longitudes en una formación de diamante  ^[5]

Robustez

Hall (2005) analiza este problema, demuestra que es robusto a las no idealizaciones, como las esquinas de bloques redondeadas y la precisión finita en la colocación de bloques, e introduce varias variantes que incluyen fuerzas de fricción distintas de cero entre bloques adyacentes.

Referencias

1. Sloane, N. J. A. (ed.). "Secuencia A014537 (Número de libros requeridos para n longitudes de libros de voladizo en el problema de apilamiento armónico de libros)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS.
2. Khoshbin-e-Khoshnazar, MR (2007). "Simplificar el modelado puede confundir a los estudiantes". Educación en Física . 42 : 14–15. doi :10.1088/0031-9120/42/1/F05. S2CID  250745206.
3. Cazelais, Gilles. "Problema de apilamiento de bloques" (PDF) . Archivado desde el original (PDF) el 4 de diciembre de 2023.
4. Joanna (14 de abril de 2022). "El problema del apilamiento infinito de bloques o la torre inclinada de Lire". Carreras de matemáticas . Consultado el 4 de diciembre de 2023 .
5. M Paterson et al., Máximo voladizo, The Mathematical Association of America, noviembre de 2009

• Hall, JF (2005). "Diversión con bloques apilables". American Journal of Physics . 73 (12): 1107–1116. Bibcode :2005AmJPh..73.1107H. doi :10.1119/1.2074007..
• Johnson, Paul B. (abril de 1955). "La torre inclinada de Lire". American Journal of Physics . 23 (4): 240. Bibcode :1955AmJPh..23..240J. doi :10.1119/1.1933957.
• Paterson, Mike ; Peres, Yuval ; Thorup, Mikkel ; Winkler, Pedro ; Zwick, Uri (2007). "Voladizo máximo". arXiv : 0707.0093 [matemáticas.HO].

Enlaces externos

• Weisstein, Eric W. "El problema de apilar libros". MathWorld .
• "Construyendo un puente infinito". Serie Infinite de PBS . 4 de mayo de 2017. Consultado el 3 de septiembre de 2018 .