Análisis de escala (matemáticas)

Técnica de resolución de problemas en matemáticas aplicadas utilizando aproximaciones de orden de magnitud

El análisis de escala (o análisis de orden de magnitud ) es una herramienta poderosa que se utiliza en las ciencias matemáticas para simplificar ecuaciones con muchos términos. Primero se determina la magnitud aproximada de los términos individuales en las ecuaciones. Luego se pueden ignorar algunos términos insignificantes.

Ejemplo: momento vertical en meteorología a escala sinóptica

Consideremos, por ejemplo, la ecuación de momento de las ecuaciones de Navier-Stokes en la dirección de coordenadas verticales de la atmósfera.

donde R es el radio de la Tierra , Ω es la frecuencia de rotación de la Tierra, g es la aceleración gravitacional , φ es la latitud, ρ es la densidad del aire y ν es la viscosidad cinemática del aire (podemos descuidar la turbulencia en la atmósfera libre ).

En escala sinóptica podemos esperar velocidades horizontales de aproximadamente U = 10 ¹  ms ⁻¹ y verticales de aproximadamente W = 10 ⁻²  ms ⁻¹ . La escala horizontal es L = 10 ⁶  m y la escala vertical es H = 10 ⁴  m. La escala de tiempo típica es T = L / U = 10 ⁵  s. Las diferencias de presión en la troposfera son Δ P = 10 ⁴  Pa ​​y la densidad del aire ρ = 10 ⁰  kg⋅m ⁻³ . Otras propiedades físicas son aproximadamente:

R = 6,378 × 10 ⁶ m;

Ω = 7,292 × 10 ⁻⁵ rad⋅s ^−1;

ν = 1,46 × 10 ⁻⁵ m ² ⋅s ^−1;

g = 9,81 m⋅s ^−2.

Se pueden realizar estimaciones de los diferentes términos de la ecuación ( A1 ) utilizando sus escalas:

${\displaystyle {\begin{aligned}{\frac {\partial w}{\partial t}}&\sim {\frac {W}{T}}\\[1.2ex]u{\frac {\partial w}{\partial x}}&\sim U{\frac {W}{L}}&\qquad v{\frac {\partial w}{\partial y}}&\sim U{\frac {W}{L}}&\qquad w{\frac {\partial w}{\partial z}}&\sim W{\frac {W}{H}}\\[1.2ex]{\frac {u^{2}}{R}}&\sim {\frac {U^{2}}{R}}&\qquad {\frac {v^{2}}{R}}&\sim {\frac {U^{2}}{R}}\\[1.2ex]{\frac {1}{\varrho }}{\frac {\partial p}{\partial z}}&\sim {\frac {1}{\varrho }}{\frac {\Delta P}{H}}&\qquad \Omega u\cos \varphi &\sim \Omega U\\[1.2ex]\nu {\frac {\partial ^{2}w}{\partial x^{2}}}&\sim \nu {\frac {W}{L^{2}}}&\qquad \nu {\frac {\partial ^{2}w}{\partial y^{2}}}&\sim \nu {\frac {W}{L^{2}}}&\qquad \nu {\frac {\partial ^{2}w}{\partial z^{2}}}&\sim \nu {\frac {W}{H^{2}}}\end{aligned}}}$

Ahora podemos introducir estas escalas y sus valores en la ecuación ( A1 ):

Podemos ver que todos los términos, excepto el primero y el segundo del lado derecho, son insignificantemente pequeños. Por lo tanto, podemos simplificar la ecuación del momento vertical a la ecuación de equilibrio hidrostático :

Reglas de análisis de escala

El análisis de escala es una herramienta muy útil y ampliamente utilizada para resolver problemas en el área de transferencia de calor y mecánica de fluidos, chorros de pared impulsados ​​por presión, flujos de separación detrás de escalones orientados hacia atrás, llamas de difusión de chorro, estudio de dinámica lineal y no lineal. El análisis de escala es un atajo eficaz para obtener soluciones aproximadas a ecuaciones que a menudo son demasiado complicadas para resolverlas con exactitud. El objetivo del análisis de escala es utilizar los principios básicos de la transferencia de calor por convección para producir estimaciones de orden de magnitud para las cantidades de interés. El análisis de escala anticipa dentro de un factor de orden uno, cuando se realiza correctamente, los costosos resultados producidos por análisis exactos. Las reglas del análisis de escala son las siguientes:

Regla 1: El primer paso en el análisis de escala es definir el dominio de extensión en el que aplicamos el análisis de escala. Cualquier análisis de escala de una región de flujo que no esté definido de manera única no es válido.

Regla 2- Una ecuación constituye una equivalencia entre las escalas de dos términos dominantes que aparecen en la ecuación. Por ejemplo,

${\displaystyle \rho c_{P}{{\partial T} \over {\partial t}}=k{\frac {\partial ^{2}T}{\partial x^{2}}}.}$

En el ejemplo anterior, el lado izquierdo podría tener el mismo orden de magnitud que el lado derecho.

Regla 3- Si en la suma de dos términos dados por

${\displaystyle c=a+b}$

El orden de magnitud de un término es mayor que el orden de magnitud del otro término

${\displaystyle O(a)>O(b)}$

entonces el orden de magnitud de la suma está dictado por el término dominante

${\displaystyle O(c)=O(a)}$

La misma conclusión se cumple si tenemos la diferencia de dos términos.

${\displaystyle c=a-b}$

Regla 4- En la suma de dos términos, si dos términos son del mismo orden de magnitud,

${\displaystyle c=a+b}$

${\displaystyle O(a)=O(b)}$

entonces la suma también es del mismo orden de magnitud:

${\displaystyle O(a)\thicksim O(b)\thicksim O(c)}$

Regla 5- En caso de producto de dos términos

${\displaystyle p=ab}$

El orden de magnitud del producto es igual al producto de los órdenes de magnitud de los dos factores.

${\displaystyle O(p)=O(a)O(b)}$

para proporciones

${\displaystyle r={\frac {a}{b}}}$

entonces

${\displaystyle O(r)={\frac {O(a)}{O(b)}}}$

Aquí O(a) representa el orden de magnitud de a.

~ representa dos términos del mismo orden de magnitud.

> representa mayor que, en el sentido de orden de magnitud.

Desarrollo del flujo en la región de entrada de un conducto de placas paralelas

Análisis de escala del flujo completamente desarrollado

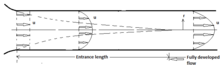
Considere el flujo laminar constante de un fluido viscoso dentro de un tubo circular. Deje que el fluido ingrese con una velocidad uniforme a lo largo de la sección transversal del flujo. A medida que el fluido se mueve hacia abajo por el tubo, se forma una capa límite de fluido de baja velocidad y crece en la superficie porque el fluido inmediatamente adyacente a la superficie tiene velocidad cero. Una característica particular y simplificadora del flujo viscoso dentro de tubos cilíndricos es el hecho de que la capa límite debe encontrarse consigo misma en la línea central del tubo, y la distribución de velocidad establece entonces un patrón fijo que es invariante. La longitud de entrada hidrodinámica es la parte del tubo en la que la capa límite de momento crece y la distribución de velocidad cambia con la longitud. La distribución de velocidad fija en la región completamente desarrollada se llama perfil de velocidad completamente desarrollado. Las ecuaciones de continuidad y conservación del momento en estado estable en bidimensionales son

Estas ecuaciones se pueden simplificar mediante el uso del análisis de escala. En cualquier punto de la zona completamente desarrollada, tenemos y . Ahora, a partir de la ecuación ( 1 ), el componente de velocidad transversal en la región completamente desarrollada se simplifica utilizando el escalamiento como ${\displaystyle x\sim L}$ ${\displaystyle y\sim \delta }$ ${\displaystyle u\sim U_{\infty }}$

En la región completamente desarrollada , de modo que la escala de la velocidad transversal es despreciable a partir de la ecuación ( 4 ). Por lo tanto, en el flujo completamente desarrollado, la ecuación de continuidad requiere que ${\displaystyle L\gg \delta }$

Con base en la ecuación ( 5 ), la ecuación del momento y ( 3 ) se reduce a

Esto significa que P es función de x únicamente. A partir de esto, la ecuación de momento x se convierte en

Cada término debe ser constante, porque el lado izquierdo es función de x solamente y el derecho es función de y . Resolviendo la ecuación ( 7 ) sujeta a la condición de contorno

Esto da como resultado la conocida solución de Hagen-Poiseuille para un flujo completamente desarrollado entre placas paralelas.

donde y se mide a partir del centro del canal. La velocidad debe ser parabólica y proporcional a la presión por unidad de longitud del conducto en la dirección del flujo.

Véase también

• Aproximación
• Análisis dimensional

Referencias

• Barenblatt, GI (1996). Escalamiento, autosimilitud y asintótica intermedia . Cambridge University Press. ISBN 0-521-43522-6.
• Tennekes, H. ; Lumley, John L. (1972). Un primer curso sobre turbulencia . MIT Press, Cambridge, Massachusetts. ISBN 0-262-20019-8.
• Bejan, A. (2004). Transferencia de calor por convección . John Wiley & sons. ISBN 978-81-265-0934-8.
• Kays, WM, Crawford ME (2012). Transferencia de calor y masa por convección . McGraw Hill Education (India). ISBN 978-1-25-902562-4.{{cite book}}: CS1 maint: multiple names: authors list (link)

Enlaces externos

• Análisis de escala y números de Reynolds Archivado el 10 de abril de 2006 en Wayback Machine.