El orden de mérito es una forma de clasificar las fuentes de energía disponibles, especialmente la generación eléctrica, en función del orden ascendente de precio (que puede reflejar el orden de sus costos marginales de producción a corto plazo) y, a veces, de contaminación, junto con la cantidad de energía que se generará. En una gestión centralizada, la clasificación es tal que las que tienen los costos marginales más bajos son las primeras en ponerse en funcionamiento para satisfacer la demanda, y las plantas con los costos marginales más altos son las últimas en ponerse en funcionamiento. El despacho de la generación de esta manera, conocido como despacho económico , minimiza el costo de producción de electricidad. A veces, las unidades generadoras deben ponerse en marcha fuera del orden de mérito, debido a la congestión de la transmisión , la confiabilidad del sistema u otras razones.
En el caso del despacho ambiental, las consideraciones adicionales relativas a la reducción de la contaminación complican aún más el problema del despacho de energía. Las limitaciones básicas del problema del despacho económico siguen vigentes, pero el modelo está optimizado para minimizar la emisión de contaminantes, además de minimizar los costos de combustible y la pérdida total de energía. [1]
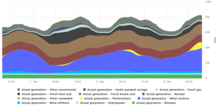
La alta demanda de electricidad durante los picos de demanda hace subir el precio de oferta de la electricidad, y la combinación de suministro de energía de base, a menudo relativamente barata, se complementa con " centrales eléctricas de pico ", que cobran una prima por su electricidad.
El aumento de la oferta de energía renovable tiende a reducir el precio medio por unidad de electricidad, porque la energía eólica y la solar tienen unos costes marginales muy bajos: no tienen que pagar por el combustible, y los únicos contribuyentes a su coste marginal son las operaciones y el mantenimiento. Como el coste suele reducirse mediante los ingresos por tarifas de alimentación, su electricidad es, como resultado, menos costosa en el mercado al contado que la del carbón o el gas natural, y las empresas de transmisión les compran primero. [2] [3] Por tanto, la electricidad solar y eólica reduce sustancialmente la cantidad de electricidad de alto precio que las empresas de transmisión necesitan comprar en horas punta, lo que reduce el coste total. Un estudio del Instituto Fraunhofer ISI concluyó que este "efecto de orden de mérito" había permitido a la energía solar reducir el precio de la electricidad en la bolsa de energía alemana en un 10% de media, y hasta en un 40% a primera hora de la tarde. En 2007 [ necesita actualización ] ; a medida que se inyecte más electricidad solar a la red, los precios de las horas punta pueden bajar aún más. [3] En 2006, el "efecto de orden de mérito" significó que los ahorros en costos de electricidad para los consumidores alemanes compensaron con creces los pagos de apoyo realizados para la generación de electricidad renovable. [3]
Un estudio de 2013 estima el efecto de orden de mérito de la generación de electricidad eólica y fotovoltaica en Alemania entre los años 2008 y 2012. Por cada GWh adicional de energías renovables que se inyecta a la red, el precio de la electricidad en el mercado diario se reduce entre 0,11 y 0,13 ¢/kWh. El efecto de orden de mérito total de la energía eólica y fotovoltaica varía de 0,5 ¢/kWh en 2010 a más de 1,1 ¢/kWh en 2012. [4]
Sin embargo, el coste marginal cero de la energía eólica y solar no se traduce en un coste marginal cero de la electricidad de carga máxima en un sistema de mercado eléctrico abierto y competitivo, ya que el suministro de energía eólica y solar por sí solo a menudo no puede despacharse para satisfacer la demanda máxima sin baterías . El propósito del orden de mérito era permitir que la electricidad de menor costo neto se despachara primero, minimizando así los costos generales del sistema eléctrico para los consumidores. La energía eólica y solar intermitente a veces puede satisfacer esta función económica. Si la oferta máxima de energía eólica (o solar) y la demanda máxima coinciden en tiempo y cantidad, la reducción de precio es mayor. Por otro lado, la energía solar tiende a ser más abundante al mediodía, mientras que la demanda máxima es a última hora de la tarde en climas cálidos, lo que da lugar a la llamada curva de pato .
Un estudio de 2008 del Instituto Fraunhofer ISI en Karlsruhe , Alemania, concluyó que la energía eólica ahorra a los consumidores alemanes 5.000 millones de euros al año. Se estima que ha reducido los precios en los países europeos con alta generación eólica entre 3 y 23 €/MWh. [5] [6] Por otro lado, la energía renovable en Alemania aumentó el precio de la electricidad: los consumidores pagan ahora 52,8 €/MWh más solo por la energía renovable (véase la Ley alemana de fuentes de energía renovable ), y el precio medio de la electricidad en Alemania ha aumentado ahora a 26 ¢/kWh. Los crecientes costes de la red eléctrica para la nueva transmisión, el comercio de mercado y el almacenamiento asociados a la energía eólica y solar no se incluyen en el coste marginal de las fuentes de energía, sino que los costes de la red se combinan con los costes de la fuente en el extremo del consumidor.
El despacho económico es la determinación a corto plazo de la producción óptima de una serie de instalaciones de generación de electricidad , para satisfacer la carga del sistema, al menor costo posible, sujeto a restricciones de transmisión y operativas. El problema del despacho económico se resuelve mediante un software informático especializado que debe satisfacer las restricciones operativas y del sistema de los recursos disponibles y las capacidades de transmisión correspondientes. En la Ley de Política Energética de los Estados Unidos de 2005 , el término se define como "la operación de las instalaciones de generación para producir energía al menor costo para servir de manera confiable a los consumidores, reconociendo cualquier límite operativo de las instalaciones de generación y transmisión". [7]
La idea principal es que, para satisfacer la demanda a un costo total mínimo, se debe utilizar primero el conjunto de generadores con los costos marginales más bajos, y el costo marginal del generador final necesario para satisfacer la demanda determina el costo marginal del sistema. Este es el costo de entregar un MWh adicional de energía al sistema. Debido a las limitaciones de transmisión, este costo puede variar en diferentes ubicaciones dentro de la red eléctrica; estos diferentes niveles de costo se identifican como " precios marginales por ubicación " (LMP, por sus siglas en inglés). La metodología histórica para el despacho económico se desarrolló para gestionar las plantas de energía que queman combustibles fósiles, basándose en cálculos que involucran las características de entrada/salida de las centrales eléctricas.
Lo siguiente se basa en Biggar y Hesamzadeh (2014) [8] y Kirschen (2010). [9] El problema del despacho económico puede considerarse como la maximización del bienestar económico W de una red eléctrica al tiempo que se cumplen las restricciones del sistema.
Para una red con n buses (nodos), supongamos que S k es la tasa de generación y D k es la tasa de consumo en el bus k . Supongamos, además, que C k ( S k ) es la función de costo de producción de energía (es decir, la tasa a la que el generador incurre en costos cuando produce a una tasa S k ), y V k ( D k ) es la tasa a la que la carga recibe valor o beneficios (expresados en unidades monetarias) cuando consume a una tasa D k . El bienestar total es entonces
La tarea del despacho económico es encontrar la combinación de tasas de producción y consumo ( S k , D k ) que maximizan esta expresión W sujeta a una serie de restricciones:
La primera restricción, necesaria para interpretar las restricciones que siguen, es que la inyección neta en cada autobús es igual a la producción total en ese autobús menos el consumo total:
La restricción de balance de potencia requiere que la suma de las inyecciones netas en todos los buses sea igual a las pérdidas de potencia en las ramas de la red:
Las pérdidas de potencia L dependen de los flujos en las ramas y, por lo tanto, de las inyecciones netas, como se muestra en la ecuación anterior. Sin embargo, no pueden depender de las inyecciones en todos los buses, ya que esto daría como resultado un sistema sobredeterminado. Por lo tanto, se elige un bus como bus de holgura y se omite de las variables de la función L. La elección del bus de holgura es completamente arbitraria; aquí se elige el bus n .
La segunda restricción implica restricciones de capacidad en el flujo de las líneas de la red. Para un sistema con m líneas, esta restricción se modela como:
donde F l es el caudal en la rama l y F l max es el valor máximo que se permite que tome este caudal. Nótese que la inyección neta en la barra de holgura no está incluida en esta ecuación por las mismas razones que las anteriores.
Estas ecuaciones ahora se pueden combinar para construir el Lagrangiano del problema de optimización:
donde π y μ son los multiplicadores lagrangianos de las restricciones. Las condiciones de optimalidad son entonces:
donde la última condición es necesaria para manejar la restricción de desigualdad en la capacidad de la línea.
Resolver estas ecuaciones es difícil desde el punto de vista computacional, ya que no son lineales e implican implícitamente la solución de las ecuaciones de flujo de potencia . El análisis se puede simplificar utilizando un modelo linealizado denominado flujo de potencia de CC.
Existe un caso especial que se encuentra en gran parte de la literatura. Se trata del caso en el que se supone que la demanda es perfectamente inelástica (es decir, no responde al precio). Esto es equivalente a suponer que para un valor muy grande de y una demanda inelástica . Bajo este supuesto, el bienestar económico total se maximiza al elegir . La tarea de despacho económico se reduce a:
Sujeto a la restricción y a las demás restricciones establecidas anteriormente.
En el despacho ambiental, las consideraciones adicionales relacionadas con la reducción de la contaminación complican aún más el problema del despacho de energía. Las restricciones básicas del problema del despacho económico siguen vigentes, pero el modelo está optimizado para minimizar la emisión de contaminantes, además de minimizar los costos de combustible y la pérdida total de energía. [1] Debido a la complejidad añadida, se han empleado varios algoritmos para optimizar este problema de despacho ambiental/económico. En particular, un algoritmo de abejas modificado que implementa principios de modelado caótico se aplicó con éxito no solo in silico , sino también en un sistema de modelo físico de generadores. [1] Otros métodos utilizados para abordar el problema del despacho de emisiones económicas incluyen la optimización de enjambre de partículas (PSO) [10] y las redes neuronales [11] .
Otra combinación notable de algoritmos se utiliza en una herramienta de emisiones en tiempo real llamada Metodología de estimación de emisiones por ubicación (LEEM, por sus siglas en inglés) que vincula el consumo de energía eléctrica y las emisiones contaminantes resultantes. [12] La LEEM estima los cambios en las emisiones asociados con los cambios incrementales en la demanda de energía derivados de la información del precio marginal por ubicación (LMP, por sus siglas en inglés) de los operadores independientes del sistema (ISO, por sus siglas en inglés) y los datos de emisiones de la Agencia de Protección Ambiental de los Estados Unidos (EPA, por sus siglas en inglés). [12] LEEM se desarrolló en la Universidad Estatal de Wayne como parte de un proyecto destinado a optimizar los sistemas de transmisión de agua en Detroit, MI, que comenzó en 2010 y desde entonces ha encontrado una aplicación más amplia como una herramienta de gestión del perfil de carga que puede ayudar a reducir los costos de generación y las emisiones. [13]
![{\displaystyle {\mathcal {L}}=\suma _{k=1}^{n}C_{k}(I_{k})+\pi \left[L(I_{1},I_{2},\dots ,I_{n-1})-\suma _{k=1}^{n}I_{k}\right]+\suma _{l=1}^{m}\mu _{l}\left[F_{l}^{max}-F_{l}(I_{1},I_{2},\dots ,I_{n-1})\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a61b0798363b176fbb66560afbeedc767089654b)
![{\displaystyle \mu _{l}\cdot \left[F_{l}^{max}-F_{l}(I_{1},I_{2},\dots ,I_{n-1})\right]=0\quad \mu _{l}\geq 0\quad k=1,\dots ,n}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7177da319002628918a4222112b2a626b3083d0)
{{cite book}}: CS1 maint: varios nombres: lista de autores ( enlace )