
En electrónica , la metaestabilidad es la capacidad de un sistema electrónico digital de persistir durante un tiempo ilimitado en un equilibrio inestable o estado metaestable . [1] En los circuitos lógicos digitales , se requiere que una señal digital esté dentro de ciertos límites de voltaje o corriente para representar un nivel lógico '0' o '1' para el funcionamiento correcto del circuito; si la señal está dentro de un rango intermedio prohibido, puede causar un comportamiento defectuoso en las puertas lógicas a las que se aplica la señal. En estados metaestables, el circuito puede ser incapaz de establecerse en un nivel lógico estable '0' o '1' dentro del tiempo requerido para el funcionamiento adecuado del circuito. Como resultado, el circuito puede actuar de formas impredecibles y puede provocar una falla del sistema, a veces denominada "falla". [2] La metaestabilidad es un ejemplo de la paradoja del asno de Buridan .
Los estados metaestables son características inherentes de los sistemas digitales asincrónicos y de los sistemas con más de un dominio de reloj independiente. En los sistemas asincrónicos con temporizador automático , los árbitros están diseñados para permitir que el sistema continúe solo después de que se haya resuelto la metaestabilidad, por lo que la metaestabilidad es una condición normal, no una condición de error. [3] En los sistemas sincrónicos con entradas asincrónicas, los sincronizadores están diseñados para hacer que la probabilidad de una falla de sincronización sea aceptablemente pequeña. [4] Los estados metaestables se pueden evitar en sistemas completamente sincrónicos cuando se satisfacen los requisitos de configuración de entrada y tiempo de retención en los flip-flops.

Un ejemplo simple de metaestabilidad se puede encontrar en un latch SR NOR , cuando tanto las entradas Set como Reset son verdaderas (R=1 y S=1) y luego ambas pasan a falsas (R=0 y S=0) aproximadamente al mismo tiempo. Ambas salidas Q y Q se mantienen inicialmente en 0 por las entradas Set y Reset simultáneas. Después de que ambas entradas Set y Reset cambien a falsas, el flip-flop terminará (eventualmente) en uno de dos estados estables, uno de Q y Q verdadero y el otro falso. El estado final dependerá de cuál de R o S regrese a cero primero, cronológicamente, pero si ambas pasan aproximadamente al mismo tiempo, la metaestabilidad resultante, con niveles de salida intermedios u oscilatorios, puede tardar arbitrariamente en resolverse a un estado estable.
En electrónica, un árbitro es un circuito diseñado para determinar cuál de varias señales llega primero. Los árbitros se utilizan en circuitos asincrónicos para ordenar las actividades computacionales de los recursos compartidos y así evitar operaciones incorrectas simultáneas. Los árbitros se utilizan en las entradas de sistemas totalmente sincrónicos y también entre dominios de reloj, como sincronizadores de señales de entrada. Aunque pueden minimizar la ocurrencia de metaestabilidad a probabilidades muy bajas, todos los árbitros tienen estados metaestables, que son inevitables en los límites de las regiones del espacio de estados de entrada, lo que da como resultado diferentes salidas. [5]
Las técnicas de diseño de circuitos sincrónicos permiten crear circuitos digitales resistentes a los modos de fallo que puede provocar la metaestabilidad. Un dominio de reloj se define como un grupo de flip-flops con un reloj común. Estas arquitecturas pueden formar un circuito que garantiza que no habrá metaestabilidad (por debajo de una determinada frecuencia máxima de reloj, por encima de la cual se produce primero la metaestabilidad y luego el fallo total), suponiendo que el reloj común es poco sesgado . Sin embargo, incluso en ese caso, si el sistema depende de cualquier entrada continua, es probable que sea vulnerable a estados metaestables. [6]
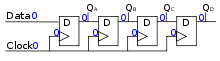
Los circuitos sincronizadores se utilizan para reducir la probabilidad de metaestabilidad cuando se recibe una entrada asincrónica o cuando se transfieren señales entre diferentes dominios de reloj. Los sincronizadores pueden adoptar la forma de una cascada de flip-flops D (por ejemplo, el registro de desplazamiento en la Figura 3). [7] Aunque cada etapa de flip-flop agrega un ciclo de reloj adicional de latencia al flujo de datos de entrada, cada etapa proporciona una oportunidad para resolver la metaestabilidad. Dichos sincronizadores pueden diseñarse para reducir la metaestabilidad a una tasa insignificante pero tolerable.
Los disparadores Schmitt también pueden utilizarse para reducir la probabilidad de metaestabilidad, pero como demostró el investigador Chaney en 1979, incluso los disparadores Schmitt pueden volverse metaestables. Además, sostuvo que no es posible eliminar por completo la posibilidad de metaestabilidad de las entradas no sincronizadas en un tiempo finito y que "existe una gran cantidad de evidencia teórica y experimental de que existe una región de comportamiento anómalo para cada dispositivo que tiene dos estados estables". Ante esta inevitabilidad, el hardware solo puede reducir la probabilidad de metaestabilidad, y los sistemas pueden intentar manejar con elegancia el evento metaestable ocasional. [8]
Aunque la metaestabilidad es bien entendida y se conocen técnicas arquitectónicas para controlarla, persiste como un modo de falla en los equipos.
Los graves errores informáticos y de hardware digital provocados por la metaestabilidad tienen una historia social fascinante. Muchos ingenieros se han negado a creer que un dispositivo biestable pueda entrar en un estado que no sea ni verdadero ni falso y que tenga una probabilidad positiva de permanecer indefinido durante un período de tiempo determinado, aunque con una probabilidad exponencialmente decreciente con el tiempo. [9] [10] [11] [12] [13] Sin embargo, la metaestabilidad es un resultado inevitable de cualquier intento de mapear un dominio continuo a uno discreto. En los límites del dominio continuo entre regiones que se mapean a diferentes salidas discretas, los puntos arbitrariamente cercanos en el dominio continuo se mapean a diferentes salidas, lo que hace que la decisión sobre qué salida seleccionar sea un proceso difícil y potencialmente largo. [14] Si las entradas a un árbitro o flip-flop llegan casi simultáneamente, lo más probable es que el circuito atraviese un punto de metaestabilidad. La metaestabilidad sigue siendo poco entendida en algunos círculos, y varios ingenieros han propuesto sus propios circuitos que se dice que resuelven o filtran la metaestabilidad; Por lo general, estos circuitos simplemente cambian la ocurrencia de metaestabilidad de un lugar a otro. [15] Los chips que utilizan múltiples fuentes de reloj a menudo se prueban con relojes de prueba que tienen relaciones de fase fijas, no los relojes independientes que se desvían entre sí que se experimentarán durante el funcionamiento. Esto generalmente evita explícitamente que se vea o se informe el modo de falla metaestable que ocurrirá en el campo. Las pruebas adecuadas de metaestabilidad con frecuencia emplean relojes de frecuencias ligeramente diferentes y aseguran el funcionamiento correcto del circuito.