Mecánica lagrangiana

Formulation of classical mechanics

Joseph Louis Lagrange (1736-1813)

En física , la mecánica de Lagrange es una formulación de la mecánica clásica basada en el principio de acción estacionaria (también conocido como principio de mínima acción). Fue introducida por el matemático y astrónomo italo-francés Joseph-Louis Lagrange en su presentación a la Academia de Ciencias de Turín en 1760 ^[1], que culminó en su gran obra de 1788, Mécanique analytique ^[2] .

La mecánica lagrangiana describe un sistema mecánico como un par ( M , L ) que consta de un espacio de configuración M y una función suave dentro de ese espacio llamada lagrangiana . Para muchos sistemas, L = T − V , donde T y V son la energía cinética y potencial del sistema, respectivamente. ^[3] ${\textstyle L}$

El principio de acción estacionaria exige que la función de acción del sistema derivada de L debe permanecer en un punto estacionario (un máximo , un mínimo o una silla ) durante toda la evolución temporal del sistema. Esta restricción permite el cálculo de las ecuaciones de movimiento del sistema utilizando las ecuaciones de Lagrange. ^[4]

Introducción

Perla sujeta a un alambre sin fricción que la obliga a moverse. El alambre ejerce una fuerza de reacción C sobre la perla para mantenerla en el alambre. La fuerza sin restricción N en este caso es la gravedad. Observe que la posición inicial de la perla en el alambre puede generar diferentes movimientos.

Péndulo simple. Como la varilla es rígida, la posición del cuerpo está restringida según la ecuación f ( x , y ) = 0 , la fuerza de restricción C es la tensión en la varilla. Nuevamente, la fuerza no restrictiva N en este caso es la gravedad.

Las leyes de Newton y el concepto de fuerzas son el punto de partida habitual para la enseñanza de los sistemas mecánicos. ^[5] Este método funciona bien para muchos problemas, pero para otros el enfoque es terriblemente complicado. ^[6] Por ejemplo, en el cálculo del movimiento de un toro que rueda sobre una superficie horizontal con una perla deslizándose en su interior, las fuerzas de restricción variables en el tiempo, como la velocidad angular del toro y el movimiento de la perla en relación con el toro, hicieron que fuera difícil determinar el movimiento del toro con las ecuaciones de Newton. ^[7] La ​​mecánica lagrangiana adopta la energía en lugar de la fuerza como su ingrediente básico, ^[5] lo que conduce a ecuaciones más abstractas capaces de abordar problemas más complejos. ^[6]

En particular, el enfoque de Lagrange fue establecer coordenadas generalizadas independientes para la posición y la velocidad de cada objeto, lo que permite escribir una forma general de lagrangiano (energía cinética total menos energía potencial del sistema) y sumar esto sobre todos los caminos posibles de movimiento de las partículas produjo una fórmula para la "acción", que minimizó para dar un conjunto generalizado de ecuaciones. Esta cantidad sumada se minimiza a lo largo del camino que realmente toma la partícula. Esta elección elimina la necesidad de que la fuerza de restricción entre en el sistema generalizado de ecuaciones resultante . Hay menos ecuaciones ya que uno no está calculando directamente la influencia de la restricción sobre la partícula en un momento dado. ^[7]

Para una amplia variedad de sistemas físicos, si el tamaño y la forma de un objeto masivo son insignificantes, es una simplificación útil tratarlo como una partícula puntual . Para un sistema de N partículas puntuales con masas m ₁ , m ₂ , ..., m _N , cada partícula tiene un vector de posición , denotado r ₁ , r ₂ , ..., r _N . Las coordenadas cartesianas suelen ser suficientes, por lo que r ₁ = ( x ₁ , y ₁ , z ₁ ) , r ₂ = ( x ₂ , y ₂ , z ₂ ) y así sucesivamente. En el espacio tridimensional , cada vector de posición requiere tres coordenadas para definir de forma única la ubicación de un punto, por lo que hay 3 N coordenadas para definir de forma única la configuración del sistema. Todos estos son puntos específicos en el espacio para ubicar las partículas; un punto general en el espacio se escribe r = ( x , y , z ) . La velocidad de cada partícula es la rapidez con la que se mueve la partícula a lo largo de su trayectoria de movimiento y es la derivada temporal de su posición, por lo tanto En la mecánica newtoniana, las ecuaciones de movimiento están dadas por las leyes de Newton . La segunda ley " fuerza neta igual a masa por aceleración " se aplica a cada partícula. Para un sistema de N partículas en 3 dimensiones, hay 3 N ecuaciones diferenciales ordinarias de segundo orden en las posiciones de las partículas para resolver. $${\displaystyle \mathbf {v} _{1}={\frac {d\mathbf {r} _{1}}{dt}},\mathbf {v} _{2}={\frac {d\mathbf {r} _{2}}{dt}},\ldots ,\mathbf {v} _{N}={\frac {d\mathbf {r} _{N}}{dt}}.}$$ $${\displaystyle \sum \mathbf {F} =m{\frac {d^{2}\mathbf {r} }{dt^{2}}},}$$

Lagrangiano

En lugar de fuerzas, la mecánica lagrangiana utiliza las energías del sistema. La cantidad central de la mecánica lagrangiana es el lagrangiano , una función que resume la dinámica de todo el sistema. En general, el lagrangiano tiene unidades de energía, pero no una expresión única para todos los sistemas físicos. Cualquier función que genere las ecuaciones de movimiento correctas, de acuerdo con las leyes físicas, puede tomarse como lagrangiana. No obstante, es posible construir expresiones generales para grandes clases de aplicaciones. El lagrangiano no relativista para un sistema de partículas en ausencia de un campo electromagnético está dado por ^[8] donde es la energía cinética total del sistema, igual a la suma Σ de las energías cinéticas de las partículas. Cada partícula etiquetada tiene masa y v _k ² = v _k · v _k es la magnitud al cuadrado de su velocidad, equivalente al producto escalar de la velocidad consigo misma. ^[9] $${\displaystyle L=T-V,}$$ $${\displaystyle T={\frac {1}{2}}\sum _{k=1}^{N}m_{k}v_{k}^{2}}$$ ${\displaystyle N}$ ${\displaystyle k}$ ${\displaystyle m_{k},}$

La energía cinética T es la energía del movimiento del sistema y es función únicamente de las velocidades v _k , no de las posiciones r _k , ni del tiempo t , por lo que T = T ( v ₁ , v ₂ , ...).

V , la energía potencial del sistema, refleja la energía de interacción entre las partículas, es decir, cuánta energía tiene cada partícula debido a todas las demás, junto con cualquier influencia externa. Para fuerzas conservativas (por ejemplo, la gravedad newtoniana ), es una función de los vectores de posición de las partículas solamente, por lo que V = V ( r ₁ , r ₂ , ...). Para aquellas fuerzas no conservativas que se pueden derivar de un potencial apropiado (por ejemplo, el potencial electromagnético ), las velocidades también aparecerán, V = V ( r ₁ , r ₂ , ..., v ₁ , v ₂ , ...). Si hay algún campo externo o fuerza impulsora externa que cambia con el tiempo, el potencial cambia con el tiempo, por lo que, en general, V = V ( r ₁ , r ₂ , ..., v ₁ , v ₂ , ..., t ).

Como ya se ha señalado, esta forma de L es aplicable a muchas clases importantes de sistemas, pero no en todas partes. Para la mecánica lagrangiana relativista debe reemplazarse en su totalidad por una función consistente con la relatividad especial (escalar bajo transformaciones de Lorentz) o la relatividad general (4-escalar). ^[10] Cuando hay un campo magnético, es necesario volver a formular la expresión de la energía potencial. ^{[ cita requerida ]} Y para las fuerzas disipativas (por ejemplo, la fricción ), debe introducirse otra función junto con la lagrangiana, a menudo denominada "función de disipación de Rayleigh", para tener en cuenta la pérdida de energía. ^[11]

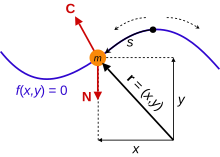
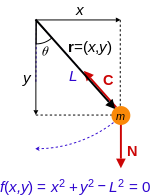
Una o más de las partículas pueden estar sujetas a una o más restricciones holonómicas ; dicha restricción se describe mediante una ecuación de la forma f ( r , t ) = 0. Si el número de restricciones en el sistema es C , entonces cada restricción tiene una ecuación f ₁ ( r , t ) = 0, f ₂ ( r , t ) = 0, ..., f _C ( r , t ) = 0, cada una de las cuales podría aplicarse a cualquiera de las partículas. Si la partícula k está sujeta a la restricción i , entonces f _i ( r _k , t ) = 0. En cualquier instante de tiempo, las coordenadas de una partícula restringida están vinculadas entre sí y no son independientes. Las ecuaciones de restricción determinan los caminos permitidos a lo largo de los cuales las partículas pueden moverse, pero no dónde están o qué tan rápido van en cada instante de tiempo. Las restricciones no holonómicas dependen de las velocidades de las partículas, aceleraciones o derivadas superiores de la posición. La mecánica lagrangiana sólo se puede aplicar a sistemas cuyas restricciones, si las hay, sean todas holonómicas . Tres ejemplos de restricciones no holonómicas son: ^[12]

Cuando las ecuaciones de restricción no son integrables, cuando las restricciones tienen desigualdades o con fuerzas no conservativas complicadas como la fricción, las restricciones no holonómicas requieren un tratamiento especial y es posible que haya que recurrir a la mecánica newtoniana o utilizar otros métodos. ^[13]

Si T o V o ambos dependen explícitamente del tiempo debido a restricciones que varían con el tiempo o influencias externas, el lagrangiano L ( r ₁ , r ₂ , ... v ₁ , v ₂ , ... t ) es explícitamente dependiente del tiempo . Si ni la energía potencial ni la cinética dependen del tiempo, entonces el lagrangiano L ( r ₁ , r ₂ , ... v ₁ , v ₂ , ...) es explícitamente independiente del tiempo . En cualquier caso, el lagrangiano siempre tiene una dependencia implícita del tiempo a través de las coordenadas generalizadas.

Con estas definiciones, las ecuaciones de Lagrange del primer tipo son ^[14]

Ecuaciones de Lagrange  (primer tipo)

${\displaystyle {\frac {\partial L}{\partial \mathbf {r} _{k}}}-{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L}{\partial {\dot {\mathbf {r} }}_{k}}}+\sum _{i=1}^{C}\lambda _{i}{\frac {\partial f_{i}}{\partial \mathbf {r} _{k}}}=0,}$

donde k = 1, 2, ..., N etiqueta las partículas, hay un multiplicador de Lagrange λ _i para cada ecuación de restricción f _i , y son cada uno abreviaturas de un vector de derivadas parciales ∂/∂ con respecto a las variables indicadas (no una derivada con respecto a todo el vector). ^{[nb 1]} Cada punto sobrepuesto es una abreviatura de una derivada temporal . Este procedimiento aumenta el número de ecuaciones para resolver en comparación con las leyes de Newton, de 3 N a 3 N + C , porque hay 3 N ecuaciones diferenciales de segundo orden acopladas en las coordenadas de posición y multiplicadores, más C ecuaciones de restricción. Sin embargo, cuando se resuelven junto con las coordenadas de posición de las partículas, los multiplicadores pueden proporcionar información sobre las fuerzas de restricción. No es necesario eliminar las coordenadas al resolver las ecuaciones de restricción. $${\displaystyle {\frac {\partial }{\partial \mathbf {r} _{k}}}\equiv \left({\frac {\partial }{\partial x_{k}}},{\frac {\partial }{\partial y_{k}}},{\frac {\partial }{\partial z_{k}}}\right),\quad {\frac {\partial }{\partial {\dot {\mathbf {r} }}_{k}}}\equiv \left({\frac {\partial }{\partial {\dot {x}}_{k}}},{\frac {\partial }{\partial {\dot {y}}_{k}}},{\frac {\partial }{\partial {\dot {z}}_{k}}}\right)}$$

En el lagrangiano, las coordenadas de posición y los componentes de velocidad son todas variables independientes , y las derivadas del lagrangiano se toman con respecto a estas por separado de acuerdo con las reglas de diferenciación habituales (por ejemplo, la derivada parcial de L con respecto al componente de velocidad z de la partícula 2, definida por v _{z ,2} = dz ₂ / dt , es simplemente ∂ L /∂ v _{z ,2} ; no es necesario utilizar reglas de cadena incómodas ni derivadas totales para relacionar el componente de velocidad con la coordenada correspondiente z ₂ ).

En cada ecuación de restricción, una coordenada es redundante porque se determina a partir de las otras coordenadas. Por lo tanto, el número de coordenadas independientes es n = 3 N − C . Podemos transformar cada vector de posición en un conjunto común de n coordenadas generalizadas , convenientemente escritas como una n -tupla q = ( q ₁ , q ₂ , ... q _n ) , expresando cada vector de posición, y por lo tanto las coordenadas de posición, como funciones de las coordenadas generalizadas y el tiempo: $${\displaystyle \mathbf {r} _{k}=\mathbf {r} _{k}(\mathbf {q} ,t)={\big (}x_{k}(\mathbf {q} ,t),y_{k}(\mathbf {q} ,t),z_{k}(\mathbf {q} ,t),t{\big )}.}$$

El vector q es un punto en el espacio de configuración del sistema. Las derivadas temporales de las coordenadas generalizadas se denominan velocidades generalizadas y, para cada partícula, la transformación de su vector de velocidad, la derivada total de su posición con respecto al tiempo, es $${\displaystyle {\dot {q}}_{j}={\frac {\mathrm {d} q_{j}}{\mathrm {d} t}},\quad \mathbf {v} _{k}=\sum _{j=1}^{n}{\frac {\partial \mathbf {r} _{k}}{\partial q_{j}}}{\dot {q}}_{j}+{\frac {\partial \mathbf {r} _{k}}{\partial t}}.}$$

Dado este v _k , la energía cinética en coordenadas generalizadas depende de las velocidades generalizadas, las coordenadas generalizadas y el tiempo si los vectores de posición dependen explícitamente del tiempo debido a restricciones que varían con el tiempo, por lo que ${\displaystyle T=T(\mathbf {q} ,{\dot {\mathbf {q} }},t).}$

Con estas definiciones, las ecuaciones de Euler-Lagrange , o ecuaciones de Lagrange de segundo tipo ^{[15] [16] [17]}

Ecuaciones de Lagrange  (segundo tipo)

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial L}{\partial {\dot {q}}_{j}}}\right)={\frac {\partial L}{\partial q_{j}}}}$

son resultados matemáticos del cálculo de variaciones , que también se pueden utilizar en mecánica. Sustituyendo en el lagrangiano L ( q , d q /d t , t ) se obtienen las ecuaciones de movimiento del sistema. El número de ecuaciones ha disminuido en comparación con la mecánica newtoniana, de 3 N a n = 3 N − C ecuaciones diferenciales de segundo orden acopladas en las coordenadas generalizadas. Estas ecuaciones no incluyen fuerzas de restricción en absoluto, solo se deben tener en cuenta las fuerzas no restrictivas.

Aunque las ecuaciones de movimiento incluyen derivadas parciales , los resultados de las derivadas parciales siguen siendo ecuaciones diferenciales ordinarias en las coordenadas de posición de las partículas. La derivada total del tiempo denotada d/d t a menudo implica una diferenciación implícita . Ambas ecuaciones son lineales en el lagrangiano, pero generalmente son ecuaciones acopladas no lineales en las coordenadas.

De la mecánica newtoniana a la lagrangiana

Leyes de Newton

Isaac Newton (1642-1727)

Para simplificar, las leyes de Newton se pueden ilustrar para una partícula sin mucha pérdida de generalidad (para un sistema de N partículas, todas estas ecuaciones se aplican a cada partícula del sistema). La ecuación de movimiento para una partícula de masa constante m es la segunda ley de Newton de 1687, en notación vectorial moderna, donde a es su aceleración y F la fuerza resultante que actúa sobre ella. Cuando la masa varía, la ecuación debe generalizarse para tomar la derivada temporal del momento. En tres dimensiones espaciales, este es un sistema de tres ecuaciones diferenciales ordinarias de segundo orden acopladas para resolver, ya que hay tres componentes en esta ecuación vectorial. La solución es el vector de posición r de la partícula en el tiempo t , sujeto a las condiciones iniciales de r y v cuando t = 0. $${\displaystyle \mathbf {F} =m\mathbf {a} ,}$$

Las leyes de Newton son fáciles de usar en coordenadas cartesianas, pero las coordenadas cartesianas no siempre son convenientes, y para otros sistemas de coordenadas las ecuaciones de movimiento pueden volverse complicadas. En un conjunto de coordenadas curvilíneas ξ = ( ξ ¹ , ξ ² , ξ ³ ), la ley en notación de índice tensorial es la "forma lagrangiana" ^{[18] [19]} donde F ^a es el a -ésimo componente contravariante de la fuerza resultante que actúa sobre la partícula, Γ ^a _bc son los símbolos de Christoffel de segundo tipo, es la energía cinética de la partícula, y g _bc los componentes covariantes del tensor métrico del sistema de coordenadas curvilíneas. Todos los índices a , b , c , toman cada uno los valores 1, 2, 3. Las coordenadas curvilíneas no son lo mismo que las coordenadas generalizadas. $${\displaystyle F^{a}=m\left({\frac {\mathrm {d} ^{2}\xi ^{a}}{\mathrm {d} t^{2}}}+\Gamma ^{a}{}_{bc}{\frac {\mathrm {d} \xi ^{b}}{\mathrm {d} t}}{\frac {\mathrm {d} \xi ^{c}}{\mathrm {d} t}}\right)=g^{ak}\left({\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial T}{\partial {\dot {\xi }}^{k}}}-{\frac {\partial T}{\partial \xi ^{k}}}\right),\quad {\dot {\xi }}^{a}\equiv {\frac {\mathrm {d} \xi ^{a}}{\mathrm {d} t}},}$$ $${\displaystyle T={\frac {1}{2}}mg_{bc}{\frac {\mathrm {d} \xi ^{b}}{\mathrm {d} t}}{\frac {\mathrm {d} \xi ^{c}}{\mathrm {d} t}}}$$

Puede parecer una complicación excesiva formular la ley de Newton de esta forma, pero tiene sus ventajas. Los componentes de aceleración en términos de los símbolos de Christoffel se pueden evitar evaluando en su lugar las derivadas de la energía cinética. Si no hay una fuerza resultante que actúe sobre la partícula, F = 0 , no se acelera, sino que se mueve con velocidad constante en línea recta. Matemáticamente, las soluciones de la ecuación diferencial son geodésicas , las curvas de longitud extrema entre dos puntos en el espacio (estas pueden terminar siendo mínimas, es decir, los caminos más cortos, pero no necesariamente). En el espacio real plano 3D, las geodésicas son simplemente líneas rectas. Entonces, para una partícula libre, la segunda ley de Newton coincide con la ecuación geodésica y establece que las partículas libres siguen geodésicas, las trayectorias extremas a lo largo de las cuales pueden moverse. Si la partícula está sujeta a fuerzas F ≠ 0 , la partícula acelera debido a las fuerzas que actúan sobre ella y se desvía de las geodésicas que seguiría si fuera libre. Con extensiones apropiadas de las cantidades dadas aquí en el espacio plano 3D al espacio-tiempo curvo 4D , la forma anterior de la ley de Newton también se traslada a la relatividad general de Einstein , en cuyo caso las partículas libres siguen geodésicas en el espacio-tiempo curvo que ya no son "líneas rectas" en el sentido ordinario. ^[20]

Sin embargo, todavía necesitamos conocer la fuerza resultante total F que actúa sobre la partícula, lo que a su vez requiere la fuerza resultante sin restricción N más la fuerza de restricción resultante C , $${\displaystyle \mathbf {F} =\mathbf {C} +\mathbf {N} .}$$

Las fuerzas de restricción pueden ser complicadas, ya que generalmente dependen del tiempo. Además, si hay restricciones, las coordenadas curvilíneas no son independientes, sino que están relacionadas por una o más ecuaciones de restricción.

Las fuerzas de restricción pueden eliminarse de las ecuaciones de movimiento, de modo que solo permanezcan las fuerzas sin restricción, o bien pueden incluirse incluyendo las ecuaciones de restricción en las ecuaciones de movimiento.

Principio de D'Alembert

Juan de Alembert (1717-1783)

Fuerza de restricción C y desplazamiento virtual δ r para una partícula de masa m confinada en una curva. La fuerza no restrictiva resultante es N .

Un resultado fundamental en la mecánica analítica es el principio de D'Alembert , introducido en 1708 por Jacques Bernoulli para comprender el equilibrio estático , y desarrollado por D'Alembert en 1743 para resolver problemas dinámicos. ^[21] El principio afirma que para N partículas el trabajo virtual, es decir, el trabajo a lo largo de un desplazamiento virtual, δ r _k , es cero: ^[9] $${\displaystyle \sum _{k=1}^{N}(\mathbf {N} _{k}+\mathbf {C} _{k}-m_{k}\mathbf {a} _{k})\cdot \delta \mathbf {r} _{k}=0.}$$

Los desplazamientos virtuales , δ r _k , son por definición cambios infinitesimales en la configuración del sistema consistentes con las fuerzas de restricción que actúan sobre el sistema en un instante de tiempo , ^[22] es decir, de tal manera que las fuerzas de restricción mantienen el movimiento restringido. No son los mismos que los desplazamientos reales en el sistema, que son causados ​​por las fuerzas resultantes de restricción y no restricción que actúan sobre la partícula para acelerarla y moverla. ^{[nb 2]} El trabajo virtual es el trabajo realizado a lo largo de un desplazamiento virtual para cualquier fuerza (restricción o no restricción).

Dado que las fuerzas de restricción actúan perpendicularmente al movimiento de cada partícula en el sistema para mantener las restricciones, el trabajo virtual total de las fuerzas de restricción que actúan sobre el sistema es cero: ^{[23] [nb 3]} de modo que $${\displaystyle \sum _{k=1}^{N}\mathbf {C} _{k}\cdot \delta \mathbf {r} _{k}=0,}$$ $${\displaystyle \sum _{k=1}^{N}(\mathbf {N} _{k}-m_{k}\mathbf {a} _{k})\cdot \delta \mathbf {r} _{k}=0.}$$

Así, el principio de D'Alembert nos permite concentrarnos sólo en las fuerzas no restrictivas aplicadas y excluir las fuerzas restrictivas en las ecuaciones de movimiento. ^{[24] [25]} La forma mostrada también es independiente de la elección de coordenadas. Sin embargo, no se puede utilizar fácilmente para establecer las ecuaciones de movimiento en un sistema de coordenadas arbitrario, ya que los desplazamientos δ r _k podrían estar conectados por una ecuación restrictiva, que nos impide establecer los N sumandos individuales en 0. Por lo tanto, buscaremos un sistema de coordenadas mutuamente independientes para el cual la suma total será 0 si y sólo si los sumandos individuales son 0. Establecer cada uno de los sumandos en 0 nos dará eventualmente nuestras ecuaciones de movimiento separadas.

Ecuaciones de movimiento a partir del principio de D'Alembert

Si existen restricciones sobre la partícula k , entonces, dado que las coordenadas de la posición r _k = ( x _k , y _k , z _k ) están vinculadas entre sí por una ecuación de restricción, también lo están las de los desplazamientos virtuales δ r _k = ( δx _k , δy _k , δz _k ) . Dado que las coordenadas generalizadas son independientes, podemos evitar las complicaciones con δ r _k convirtiendo a desplazamientos virtuales en las coordenadas generalizadas. Estos están relacionados de la misma forma que una diferencial total , ^[9] $${\displaystyle \delta \mathbf {r} _{k}=\sum _{j=1}^{n}{\frac {\partial \mathbf {r} _{k}}{\partial q_{j}}}\delta q_{j}.}$$

No existe una derivada temporal parcial con respecto al tiempo multiplicado por un incremento de tiempo, ya que se trata de un desplazamiento virtual, a lo largo de las restricciones en un instante de tiempo.

El primer término del principio de D'Alembert anterior es el trabajo virtual realizado por las fuerzas no restrictivas N _k a lo largo de los desplazamientos virtuales δ r _k , y puede, sin pérdida de generalidad, convertirse en análogos generalizados mediante la definición de fuerzas generalizadas de modo que $${\displaystyle Q_{j}=\sum _{k=1}^{N}\mathbf {N} _{k}\cdot {\frac {\partial \mathbf {r} _{k}}{\partial q_{j}}},}$$ $${\displaystyle \sum _{k=1}^{N}\mathbf {N} _{k}\cdot \delta \mathbf {r} _{k}=\sum _{k=1}^{N}\mathbf {N} _{k}\cdot \sum _{j=1}^{n}{\frac {\partial \mathbf {r} _{k}}{\partial q_{j}}}\delta q_{j}=\sum _{j=1}^{n}Q_{j}\delta q_{j}.}$$

Esta es la mitad de la conversión a coordenadas generalizadas. Queda por convertir el término de aceleración a coordenadas generalizadas, lo cual no es inmediatamente obvio. Recordando la forma de Lagrange de la segunda ley de Newton, se pueden hallar las derivadas parciales de la energía cinética con respecto a las coordenadas generalizadas y las velocidades para obtener el resultado deseado: ^[9] $${\displaystyle \sum _{k=1}^{N}m_{k}\mathbf {a} _{k}\cdot {\frac {\partial \mathbf {r} _{k}}{\partial q_{j}}}={\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial T}{\partial {\dot {q}}_{j}}}-{\frac {\partial T}{\partial q_{j}}}.}$$

Ahora bien, el principio de D'Alembert está en las coordenadas generalizadas como se requiere, y dado que estos desplazamientos virtuales δq _j son independientes y distintos de cero, los coeficientes se pueden igualar a cero, lo que da como resultado las ecuaciones de Lagrange ^{[26] [27]} o las ecuaciones generalizadas de movimiento ^[28]. $${\displaystyle \sum _{j=1}^{n}\left[Q_{j}-\left({\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial T}{\partial {\dot {q}}_{j}}}-{\frac {\partial T}{\partial q_{j}}}\right)\right]\delta q_{j}=0,}$$ $${\displaystyle Q_{j}={\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial T}{\partial {\dot {q}}_{j}}}-{\frac {\partial T}{\partial q_{j}}}}$$

Estas ecuaciones son equivalentes a las leyes de Newton para las fuerzas sin restricciones . Las fuerzas generalizadas en esta ecuación se derivan únicamente de las fuerzas sin restricciones; las fuerzas con restricciones se han excluido del principio de D'Alembert y no es necesario encontrarlas. Las fuerzas generalizadas pueden ser no conservativas, siempre que satisfagan el principio de D'Alembert. ^[29]

Ecuaciones de Euler-Lagrange y principio de Hamilton

A medida que el sistema evoluciona, q traza un camino a través del espacio de configuración (solo se muestran algunas). El camino que sigue el sistema (rojo) tiene una acción estacionaria (δ S = 0) ante pequeños cambios en la configuración del sistema (δ q ). ^[30]

Para una fuerza no conservativa que depende de la velocidad, puede ser posible encontrar una función de energía potencial V que dependa de posiciones y velocidades. Si las fuerzas generalizadas Q _i pueden derivarse de un potencial V tal que ^{[31] [32]} igualando a las ecuaciones de Lagrange y definiendo el lagrangiano como L = T − V se obtienen las ecuaciones de Lagrange de segundo tipo o las ecuaciones de movimiento de Euler-Lagrange $${\displaystyle Q_{j}={\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial V}{\partial {\dot {q}}_{j}}}-{\frac {\partial V}{\partial q_{j}}},}$$ $${\displaystyle {\frac {\partial L}{\partial q_{j}}}-{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L}{\partial {\dot {q}}_{j}}}=0.}$$

Sin embargo, las ecuaciones de Euler-Lagrange solo pueden dar cuenta de fuerzas no conservativas si se puede encontrar un potencial como se muestra. Esto puede no ser siempre posible para fuerzas no conservativas, y las ecuaciones de Lagrange no involucran ningún potencial, solo fuerzas generalizadas; por lo tanto, son más generales que las ecuaciones de Euler-Lagrange.

Las ecuaciones de Euler-Lagrange también se deducen del cálculo de variaciones . La variación del lagrangiano es que tiene una forma similar a la diferencial total de L , pero los desplazamientos virtuales y sus derivadas temporales reemplazan a las diferenciales, y no hay incremento temporal de acuerdo con la definición de los desplazamientos virtuales. Una integración por partes con respecto al tiempo puede transferir la derivada temporal de δq _j a ∂ L /∂(d q _j /d t ), en el proceso intercambiando d( δq _j )/d t por δq _j , lo que permite factorizar los desplazamientos virtuales independientes a partir de las derivadas del lagrangiano, $${\displaystyle \delta L=\sum _{j=1}^{n}\left({\frac {\partial L}{\partial q_{j}}}\delta q_{j}+{\frac {\partial L}{\partial {\dot {q}}_{j}}}\delta {\dot {q}}_{j}\right),\quad \delta {\dot {q}}_{j}\equiv \delta {\frac {\mathrm {d} q_{j}}{\mathrm {d} t}}\equiv {\frac {\mathrm {d} (\delta q_{j})}{\mathrm {d} t}},}$$ $${\displaystyle {\begin{aligned}\int _{t_{1}}^{t_{2}}\delta L\,\mathrm {d} t&=\int _{t_{1}}^{t_{2}}\sum _{j=1}^{n}\left({\frac {\partial L}{\partial q_{j}}}\delta q_{j}+{\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial L}{\partial {\dot {q}}_{j}}}\delta q_{j}\right)-{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L}{\partial {\dot {q}}_{j}}}\delta q_{j}\right)\,\mathrm {d} t\\&=\sum _{j=1}^{n}\left[{\frac {\partial L}{\partial {\dot {q}}_{j}}}\delta q_{j}\right]_{t_{1}}^{t_{2}}+\int _{t_{1}}^{t_{2}}\sum _{j=1}^{n}\left({\frac {\partial L}{\partial q_{j}}}-{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L}{\partial {\dot {q}}_{j}}}\right)\delta q_{j}\,\mathrm {d} t.\end{aligned}}}$$

Ahora bien, si la condición δq _j ( t ₁ ) = δq _j ( t ₂ ) = 0 se cumple para todo j , los términos no integrados son cero. Si además la integral temporal completa de δL es cero, entonces, como los δq _j son independientes y la única forma de que una integral definida sea cero es si el integrando es igual a cero, cada uno de los coeficientes de δq _j también debe ser cero. Entonces obtenemos las ecuaciones de movimiento. Esto se puede resumir mediante el principio de Hamilton : $${\displaystyle \int _{t_{1}}^{t_{2}}\delta L\,\mathrm {d} t=0.}$$

La integral temporal del lagrangiano es otra cantidad llamada acción , definida como ^[33] que es una función ; toma la función lagrangiana para todos los tiempos entre t ₁ y t ₂ y devuelve un valor escalar. Sus dimensiones son las mismas que [ momento angular ], [energía]·[tiempo] o [longitud]·[momento]. Con esta definición, el principio de Hamilton es $${\displaystyle S=\int _{t_{1}}^{t_{2}}L\,\mathrm {d} t,}$$ $${\displaystyle \delta S=0.}$$

En lugar de pensar en partículas que se aceleran en respuesta a fuerzas aplicadas, se podría pensar en ellas eligiendo el camino con una acción estacionaria, con los puntos finales del camino en el espacio de configuración mantenidos fijos en los tiempos inicial y final. El principio de Hamilton es uno de varios principios de acción . ^[34]

Históricamente, la idea de encontrar el camino más corto que una partícula puede seguir sujeta a una fuerza motivó las primeras aplicaciones del cálculo de variaciones a problemas mecánicos, como el problema de la braquistócrona resuelto por Jean Bernoulli en 1696, así como Leibniz , Daniel Bernoulli , L'Hôpital en la misma época y Newton al año siguiente. ^[35] El propio Newton estaba pensando en la línea del cálculo variacional, pero no publicó. ^[35] Estas ideas a su vez conducen a los principios variacionales de la mecánica, de Fermat , Maupertuis , Euler , Hamilton y otros.

El principio de Hamilton se puede aplicar a restricciones no holonómicas si las ecuaciones de restricción se pueden poner en una forma determinada, una combinación lineal de diferenciales de primer orden en las coordenadas. La ecuación de restricción resultante se puede reorganizar en una ecuación diferencial de primer orden. ^[36] Esto no se explicará aquí.

Multiplicadores y restricciones de Lagrange

El lagrangiano L puede variarse en las coordenadas cartesianas r _k , para N partículas, $${\displaystyle \int _{t_{1}}^{t_{2}}\sum _{k=1}^{N}\left({\frac {\partial L}{\partial \mathbf {r} _{k}}}-{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L}{\partial {\dot {\mathbf {r} }}_{k}}}\right)\cdot \delta \mathbf {r} _{k}\,\mathrm {d} t=0.}$$

El principio de Hamilton sigue siendo válido incluso si las coordenadas en las que se expresa L no son independientes, aquí r _k , pero se sigue suponiendo que las restricciones son holonómicas. ^[37] Como siempre, los puntos finales son fijos δ r _k ( t ₁ ) = δ r _k ( t ₂ ) = 0 para todo k . Lo que no se puede hacer es simplemente igualar los coeficientes de δ r _k a cero porque los δ r _k no son independientes. En cambio, se puede utilizar el método de los multiplicadores de Lagrange para incluir las restricciones. Al multiplicar cada ecuación de restricción f _i ( r _k , t ) = 0 por un multiplicador de Lagrange λ _i para i = 1, 2, ..., C , y sumar los resultados al lagrangiano original, se obtiene el nuevo lagrangiano $${\displaystyle L'=L(\mathbf {r} _{1},\mathbf {r} _{2},\ldots ,{\dot {\mathbf {r} }}_{1},{\dot {\mathbf {r} }}_{2},\ldots ,t)+\sum _{i=1}^{C}\lambda _{i}(t)f_{i}(\mathbf {r} _{k},t).}$$

Los multiplicadores de Lagrange son funciones arbitrarias del tiempo t , pero no funciones de las coordenadas rk , por lo que los multiplicadores están en igualdad de condiciones con las coordenadas de posición. Variando este nuevo lagrangiano e integrando con respecto al tiempo se _obtiene $${\displaystyle \int _{t_{1}}^{t_{2}}\delta L'\mathrm {d} t=\int _{t_{1}}^{t_{2}}\sum _{k=1}^{N}\left({\frac {\partial L}{\partial \mathbf {r} _{k}}}-{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L}{\partial {\dot {\mathbf {r} }}_{k}}}+\sum _{i=1}^{C}\lambda _{i}{\frac {\partial f_{i}}{\partial \mathbf {r} _{k}}}\right)\cdot \delta \mathbf {r} _{k}\,\mathrm {d} t=0.}$$

Los multiplicadores introducidos se pueden hallar de modo que los coeficientes de δ r _k sean cero, aunque r _k no sean independientes. De ello se deducen las ecuaciones de movimiento. A partir del análisis anterior, obtener la solución de esta integral es equivalente a afirmar que son ecuaciones de Lagrange de primera especie . Además, las ecuaciones de Euler-Lagrange λ _i para el nuevo lagrangiano devuelven las ecuaciones de restricción $${\displaystyle {\frac {\partial L'}{\partial \mathbf {r} _{k}}}-{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L'}{\partial {\dot {\mathbf {r} }}_{k}}}=0\quad \Rightarrow \quad {\frac {\partial L}{\partial \mathbf {r} _{k}}}-{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L}{\partial {\dot {\mathbf {r} }}_{k}}}+\sum _{i=1}^{C}\lambda _{i}{\frac {\partial f_{i}}{\partial \mathbf {r} _{k}}}=0,}$$ $${\displaystyle {\frac {\partial L'}{\partial \lambda _{i}}}-{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L'}{\partial {\dot {\lambda }}_{i}}}=0\quad \Rightarrow \quad f_{i}(\mathbf {r} _{k},t)=0.}$$

Para el caso de una fuerza conservativa dada por el gradiente de alguna energía potencial V , una función de las coordenadas r _{k solamente, sustituyendo el Lagrangiano} L = T − V se obtiene e identificando las derivadas de la energía cinética como la (negativa de la) fuerza resultante, y las derivadas del potencial igualando la fuerza sin restricción, se deduce que las fuerzas de restricción están dando las fuerzas de restricción explícitamente en términos de las ecuaciones de restricción y los multiplicadores de Lagrange. $${\displaystyle \underbrace {{\frac {\partial T}{\partial \mathbf {r} _{k}}}-{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial T}{\partial {\dot {\mathbf {r} }}_{k}}}} _{-\mathbf {F} _{k}}+\underbrace {-{\frac {\partial V}{\partial \mathbf {r} _{k}}}} _{\mathbf {N} _{k}}+\sum _{i=1}^{C}\lambda _{i}{\frac {\partial f_{i}}{\partial \mathbf {r} _{k}}}=0,}$$ $${\displaystyle \mathbf {C} _{k}=\sum _{i=1}^{C}\lambda _{i}{\frac {\partial f_{i}}{\partial \mathbf {r} _{k}}},}$$

Propiedades del Lagrangiano

No unicidad

El lagrangiano de un sistema dado no es único. Un lagrangiano L puede multiplicarse por una constante distinta de cero a y desplazarse por una constante arbitraria b , y el nuevo lagrangiano L ′ = aL + b describirá el mismo movimiento que L . Si uno restringe como arriba a trayectorias q sobre un intervalo de tiempo dado [ t _st , t _fin ] } y puntos finales fijos P _st = q ( t _st ) y P _fin = q ( t _fin ) , entonces dos lagrangianos que describen el mismo sistema pueden diferir por la "derivada temporal total" de una función f ( q , t ) : ^[38] donde significa $${\displaystyle L'(\mathbf {q} ,{\dot {\mathbf {q} }},t)=L(\mathbf {q} ,{\dot {\mathbf {q} }},t)+{\frac {\mathrm {d} f(\mathbf {q} ,t)}{\mathrm {d} t}},}$$ ${\textstyle {\frac {\mathrm {d} f(\mathbf {q} ,t)}{\mathrm {d} t}}}$ ${\textstyle {\frac {\partial f(\mathbf {q} ,t)}{\partial t}}+\sum _{i}{\frac {\partial f(\mathbf {q} ,t)}{\partial q_{i}}}{\dot {q}}_{i}.}$

Ambos lagrangianos L y L ′ producen las mismas ecuaciones de movimiento ^{[39] [40]} ya que las acciones correspondientes S y S ′ están relacionadas a través de los dos últimos componentes f ( P _fin , t _fin ) y f ( P _st , t _st ) independientes de q . $${\displaystyle {\begin{aligned}S'[\mathbf {q} ]&=\int _{t_{\text{st}}}^{t_{\text{fin}}}L'(\mathbf {q} (t),{\dot {\mathbf {q} }}(t),t)\,dt\\&=\int _{t_{\text{st}}}^{t_{\text{fin}}}L(\mathbf {q} (t),{\dot {\mathbf {q} }}(t),t)\,dt+\int _{t_{\text{st}}}^{t_{\text{fin}}}{\frac {\mathrm {d} f(\mathbf {q} (t),t)}{\mathrm {d} t}}\,dt\\&=S[\mathbf {q} ]+f(P_{\text{fin}},t_{\text{fin}})-f(P_{\text{st}},t_{\text{st}}),\end{aligned}}}$$

Invariancia bajo transformaciones puntuales

Dado un conjunto de coordenadas generalizadas q , si cambiamos estas variables a un nuevo conjunto de coordenadas generalizadas Q de acuerdo con una transformación de puntos Q = Q ( q , t ) que es invertible cuando q = q ( Q , t ) , el nuevo Lagrangiano L ′ es una función de las nuevas coordenadas y por la regla de la cadena para la diferenciación parcial, las ecuaciones de Lagrange son invariantes bajo esta transformación; ^[41] $${\displaystyle L'(\mathbf {Q} ,{\dot {\mathbf {Q} }},t)=L(\mathbf {q} (\mathbf {Q} ,t),{\dot {\mathbf {q} }}(\mathbf {Q} ,{\dot {\mathbf {Q} }},t),t),}$$ $${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L'}{\partial {\dot {Q}}_{i}}}={\frac {\partial L'}{\partial Q_{i}}}.}$$

Esto puede simplificar las ecuaciones de movimiento.

Prueba

Para una transformación de coordenadas , tenemos que implica que lo que implica que . ${\displaystyle Q_{i}=Q_{i}(\mathbf {q} ,t)}$ $${\displaystyle d{Q_{i}}=\sum _{k}{\frac {\partial Q_{i}}{\partial q_{k}}}d{q_{k}}+{\frac {\partial Q_{k}}{\partial t}}dt,}$$ ${\displaystyle {\dot {Q_{i}}}=\sum _{k}{\frac {\partial Q_{i}}{\partial q_{k}}}(\mathbf {q} ,t)\,{\dot {q}}_{k}+{\frac {\partial Q_{k}}{\partial t}}(\mathbf {q} ,t)}$ ${\displaystyle {\frac {\partial {\dot {Q_{i}}}}{\partial {\dot {q}}_{k}}}={\frac {\partial Q_{i}}{\partial q_{k}}}}$

También se sigue que: y de manera similar: lo que implica que . Las dos relaciones derivadas pueden emplearse en la prueba. $${\displaystyle {\frac {\partial {\dot {Q_{i}}}}{\partial q_{j}}}=\sum _{k}{\frac {\partial ^{2}Q_{i}}{\partial q_{j}\partial q_{k}}}(\mathbf {q} ,t)\,{\dot {q}}_{k}+{\frac {\partial ^{2}Q_{k}}{\partial q_{j}\partial t}}(\mathbf {q} ,t)}$$ $${\displaystyle {\frac {d}{dt}}\left({\frac {\partial {Q_{i}}}{\partial q_{j}}}\right)=\sum _{k}{\frac {\partial ^{2}Q_{i}}{\partial q_{k}\partial q_{j}}}(\mathbf {q} ,t)\,{\dot {q}}_{k}+{\frac {\partial ^{2}Q_{k}}{\partial t\partial q_{j}}}(\mathbf {q} ,t)}$$ ${\displaystyle {\frac {d}{dt}}\left({\frac {\partial Q_{i}}{\partial q_{k}}}\right)={\frac {\partial {\dot {Q}}_{i}}{\partial q_{k}}}}$

Partiendo de las ecuaciones de Euler Lagrange en el conjunto inicial de coordenadas generalizadas, tenemos: $${\displaystyle {\begin{aligned}{\frac {d}{dt}}{\frac {\partial L}{\partial {\dot {q}}_{i}}}-{\frac {{\partial }L}{\partial q_{i}}}=0\\\sum _{k}\left({\frac {d}{dt}}\left({\frac {\partial L}{\partial {\dot {Q}}_{k}}}{\frac {\partial {\dot {Q}}_{k}}{\partial {\dot {q}}_{i}}}\right)-{\frac {{\partial }L}{\partial Q_{k}}}{\frac {\partial Q_{k}}{\partial {q}_{i}}}-{\frac {{\partial }L}{\partial {\dot {Q}}_{k}}}{\frac {\partial {\dot {Q}}_{k}}{\partial {q}_{i}}}\right)=0\\\sum _{k}\left({\frac {d}{dt}}\left({\frac {\partial L}{\partial {\dot {Q}}_{k}}}\right){\frac {\partial {\dot {Q}}_{k}}{\partial {\dot {q}}_{i}}}+{\frac {\partial L}{\partial {\dot {Q}}_{k}}}{\frac {d}{dt}}\left({\frac {\partial {\dot {Q}}_{k}}{\partial {\dot {q}}_{i}}}\right)-{\frac {{\partial }L}{\partial Q_{k}}}{\frac {\partial {\dot {Q}}_{k}}{\partial {\dot {q}}_{i}}}-{\frac {{\partial }L}{\partial {\dot {Q}}_{k}}}{\frac {d}{dt}}\left({\frac {\partial Q_{k}}{\partial q_{i}}}\right)\right)=0\\\sum _{k}\left({\frac {d}{dt}}\left({\frac {\partial L}{\partial {\dot {Q}}_{k}}}\right)-{\frac {\partial L}{\partial {\dot {Q}}_{k}}}\right){\frac {\partial Q_{k}}{\partial q_{i}}}=0\\\end{aligned}}}$$

Dado que la transformación de es invertible, se deduce que la forma de la ecuación de Euler-Lagrange es invariante, es decir, ${\displaystyle q\rightarrow Q}$ $${\displaystyle {\frac {d}{dt}}{\frac {\partial L}{\partial {\dot {Q}}_{i}}}-{\frac {{\partial }L}{\partial Q_{i}}}=0.}$$

Coordenadas cíclicas y momentos conservados

Una propiedad importante del lagrangiano es que las cantidades conservadas se pueden leer fácilmente a partir de él. El momento generalizado "canónicamente conjugado con" la coordenada q _i se define por $${\displaystyle p_{i}={\frac {\partial L}{\partial {\dot {q}}_{i}}}.}$$

Si el lagrangiano L no depende de ninguna coordenada q _i , se sigue inmediatamente de las ecuaciones de Euler-Lagrange que y al integrar se muestra que el momento generalizado correspondiente es igual a una constante, una cantidad conservada. Este es un caso especial del teorema de Noether . Tales coordenadas se denominan "cíclicas" o "ignorables". $${\displaystyle {\dot {p}}_{i}={\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L}{\partial {\dot {q}}_{i}}}={\frac {\partial L}{\partial q_{i}}}=0}$$

Por ejemplo, un sistema puede tener un Lagrangiano donde r y z son longitudes a lo largo de líneas rectas, s es una longitud de arco a lo largo de alguna curva, y θ y φ son ángulos. Nótese que z , s y φ están todos ausentes en el Lagrangiano aunque sus velocidades no lo estén. Entonces los momentos son todos cantidades conservadas. Las unidades y la naturaleza de cada momento generalizado dependerán de la coordenada correspondiente; en este caso p _z es un momento de traslación en la dirección z , p _s es también un momento de traslación a lo largo de la curva en la que se mide s , y p _φ es un momento angular en el plano en el que se mide el ángulo φ . Por más complicado que sea el movimiento del sistema, todas las coordenadas y velocidades variarán de tal manera que estos momentos se conservan. $${\displaystyle L(r,\theta ,{\dot {s}},{\dot {z}},{\dot {r}},{\dot {\theta }},{\dot {\phi }},t),}$$ $${\displaystyle p_{z}={\frac {\partial L}{\partial {\dot {z}}}},\quad p_{s}={\frac {\partial L}{\partial {\dot {s}}}},\quad p_{\phi }={\frac {\partial L}{\partial {\dot {\phi }}}},}$$

Energía

Dado un lagrangiano, el hamiltoniano del sistema mecánico correspondiente es, por definición, Esta cantidad será equivalente a energía si las coordenadas generalizadas son coordenadas naturales, es decir, no tienen dependencia explícita del tiempo al expresar el vector de posición: . De: donde es una matriz simétrica que se define para la derivación. ${\displaystyle L,}$ $${\displaystyle H={\biggl (}\sum _{i=1}^{n}{\dot {q}}_{i}{\frac {\partial L}{\partial {\dot {q}}_{i}}}{\biggr )}-L.}$$ ${\displaystyle \mathbf {r} =\mathbf {r} (q_{1},\cdots ,q_{n})}$ $${\displaystyle T={\frac {m}{2}}v^{2}={\frac {m}{2}}\sum _{i,j}\left({\frac {\partial {\vec {r}}}{\partial q_{i}}}{\dot {q}}_{i}\right)\cdot \left({\frac {\partial {\vec {r}}}{\partial q_{j}}}{\dot {q}}_{j}\right)={\frac {m}{2}}\sum _{i,j}a_{ij}{\dot {q}}_{i}{\dot {q}}_{j}}$$ $${\displaystyle \sum _{k=1}^{n}{\dot {q}}_{k}{\frac {\partial L}{\partial {\dot {q}}_{k}}}=\sum _{k=1}^{n}{\dot {q}}_{k}{\frac {\partial T}{\partial {\dot {q}}_{k}}}={\frac {m}{2}}\left(2\sum _{i,j}a_{ij}{\dot {q}}_{i}{\dot {q}}_{j}\right)=2T}$$ $${\displaystyle H=\left(\sum _{i=1}^{n}{\dot {q}}_{i}{\frac {\partial L}{\partial {\dot {q}}_{i}}}\right)-L=2T-(T-V)=T+V=E}$$ ${\displaystyle a_{ij}={\frac {\partial \mathbf {r} }{\partial q_{i}}}\cdot {\frac {\partial \mathbf {r} }{\partial q_{j}}}}$

Invariancia bajo transformaciones de coordenadas

En cada instante de tiempo t , la energía es invariante bajo los cambios de coordenadas del espacio de configuración q → Q , es decir (usando coordenadas naturales) Además de este resultado, la prueba a continuación muestra que, bajo tal cambio de coordenadas, las derivadas cambian como coeficientes de una forma lineal. $${\displaystyle E(\mathbf {q} ,{\dot {\mathbf {q} }},t)=E(\mathbf {Q} ,{\dot {\mathbf {Q} }},t).}$$ ${\displaystyle \partial L/\partial {\dot {q}}_{i}}$

Prueba

Para una transformación de coordenadas Q = F ( q ) , tenemos donde es la función tangente del espacio vectorial al espacio vectorial y es el jacobiano. En las coordenadas y la fórmula anterior para tiene la forma Después de la diferenciación que involucra la regla del producto, donde $${\displaystyle d\mathbf {Q} =F_{*}(\mathbf {q} )d\mathbf {q} ,}$$ ${\displaystyle F_{*}(\mathbf {q} )}$ $${\displaystyle \left\{\sum _{i=1}^{n}{\dot {q}}_{i}\cdot \left(\left.{\frac {\partial }{\partial q_{i}}}\right|_{\mathbf {q} }\right)\ {\biggl |}\ {\dot {q}}_{i}\in \mathbb {R} \right\}}$$ $${\displaystyle \left\{\sum _{i=1}^{n}{\dot {Q}}_{i}\cdot \left(\left.{\frac {\partial }{\partial Q_{i}}}\right|_{F(\mathbf {q} )}\right)\ {\biggl |}\ {\dot {Q}}_{i}\in \mathbb {R} \right\},}$$ $${\displaystyle \textstyle F_{*}(\mathbf {q} )=\left(\left.{\frac {\partial F_{i}}{\partial q_{j}}}\right|_{\mathbf {q} }\right)_{i,j=1}^{n}}$$ ${\displaystyle {\dot {q}}_{i}}$ ${\displaystyle {\dot {Q}}_{i},}$ ${\displaystyle d\mathbf {Q} }$ ${\displaystyle {\dot {\mathbf {Q} }}=F_{*}(\mathbf {q} ){\dot {\mathbf {q} }}.}$ $${\displaystyle d{\dot {\mathbf {Q} }}=G(\mathbf {q} ,{\dot {\mathbf {q} }})d\mathbf {q} +F_{*}(\mathbf {q} )d{\dot {\mathbf {q} }},}$$ $${\displaystyle {\begin{aligned}G(\mathbf {q} ,{\dot {\mathbf {q} }})d\mathbf {q} &\,{\stackrel {\text{def}}{=}}\,d(F_{*}(\mathbf {q} )){\dot {\mathbf {q} }}=\left(\sum _{k=1}^{n}{\frac {\partial ^{2}F_{i}}{\partial q_{j}\partial q_{k}}}{\biggl |}_{\mathbf {q} }dq_{k}\right)_{i,j=1}^{n}{\dot {\mathbf {q} }}=\left(\sum _{j=1}^{n}{\dot {q}}_{j}\sum _{k=1}^{n}{\frac {\partial ^{2}F_{i}}{\partial q_{j}\partial q_{k}}}{\biggl |}_{\mathbf {q} }dq_{k}\right)_{i=1,\ldots ,n}^{T}\\&=\left(\sum _{k=1}^{n}dq_{k}\sum _{j=1}^{n}{\frac {\partial ^{2}F_{i}}{\partial q_{j}\partial q_{k}}}{\biggl |}_{\mathbf {q} }{\dot {q}}_{j}\right)_{i=1,\ldots ,n}^{T}=\left(\sum _{j=1}^{n}{\frac {\partial ^{2}F_{i}}{\partial q_{j}\partial q_{k}}}{\biggl |}_{\mathbf {q} }{\dot {q}}_{j}\right)_{i,k=1}^{n}d\mathbf {q} .\end{aligned}}}$$

En notación vectorial, $${\displaystyle {\begin{aligned}dL(\mathbf {Q} ,{\dot {\mathbf {Q} }},t)&={\frac {\partial L}{\partial \mathbf {Q} }}d\mathbf {Q} +{\frac {\partial L}{\partial {\dot {\mathbf {Q} }}}}d{\dot {\mathbf {Q} }}+{\frac {\partial L}{\partial t}}dt\\&=\left({\frac {\partial L}{\partial \mathbf {Q} }}F_{*}(\mathbf {q} )+{\frac {\partial L}{\partial {\dot {\mathbf {Q} }}}}G(\mathbf {q} ,{\dot {\mathbf {q} }})\right)d\mathbf {q} +{\frac {\partial L}{\partial {\dot {\mathbf {Q} }}}}F_{*}(\mathbf {q} )d{\dot {\mathbf {q} }}+{\frac {\partial L}{\partial t}}.\end{aligned}}}$$

Por otro lado, $${\displaystyle dL(\mathbf {q} ,{\dot {\mathbf {q} }},t)={\frac {\partial L}{\partial \mathbf {q} }}d\mathbf {q} +{\frac {\partial L}{\partial {\dot {\mathbf {q} }}}}d{\dot {\mathbf {q} }}+{\frac {\partial L}{\partial t}}dt.}$$

Se mencionó anteriormente que los lagrangianos no dependen de la elección de las coordenadas del espacio de configuración, es decir, una implicación de esto es que y Esto demuestra que, para cada y es una forma lineal bien definida cuyos coeficientes son 1-tensores contravariantes. Al aplicar ambos lados de la ecuación a y usar la fórmula anterior para se obtiene la invariancia de la energía . ${\displaystyle L(\mathbf {Q} ,{\dot {\mathbf {Q} }},t)=L(\mathbf {q} ,{\dot {\mathbf {q} }},t).}$ ${\displaystyle dL(\mathbf {Q} ,{\dot {\mathbf {Q} }},t)=dL(\mathbf {q} ,{\dot {\mathbf {q} }},t),}$ $${\displaystyle {\frac {\partial L}{\partial {\dot {\mathbf {Q} }}}}F_{*}(\mathbf {q} )={\frac {\partial L}{\partial {\dot {\mathbf {q} }}}}.}$$ ${\displaystyle \mathbf {q} ,}$ ${\displaystyle {\dot {\mathbf {q} }},}$ ${\displaystyle t,}$ ${\displaystyle \textstyle \sum \limits _{i=1}^{n}{\frac {\partial L}{\partial {\dot {q}}_{i}}}d{\dot {q}}_{i}}$ ${\displaystyle \textstyle {\frac {\partial L}{\partial {\dot {q}}_{i}}}}$ ${\displaystyle {\dot {\mathbf {q} }}}$ ${\displaystyle {\dot {\mathbf {Q} }}}$ $${\displaystyle {\dot {\mathbf {Q} }}{\frac {\partial L}{\partial {\dot {\mathbf {Q} }}}}={\dot {\mathbf {q} }}{\frac {\partial L}{\partial {\dot {\mathbf {q} }}}}.}$$ ${\displaystyle E}$

Conservación

En la mecánica lagrangiana, el sistema es cerrado si y solo si su lagrangiano no depende explícitamente del tiempo. La ley de conservación de la energía establece que la energía de un sistema cerrado es una integral del movimiento . ${\displaystyle L}$ ${\displaystyle E}$

Más precisamente, sea q = q ( t ) un extremal . (En otras palabras, q satisface las ecuaciones de Euler-Lagrange). Tomando la derivada temporal total de L a lo largo de este extremal y utilizando las ecuaciones EL se llega a $${\displaystyle {\begin{aligned}{\frac {dL}{dt}}&={\dot {\mathbf {q} }}{\frac {\partial L}{\partial \mathbf {q} }}+{\ddot {\mathbf {q} }}{\frac {\partial L}{\partial \mathbf {\dot {q}} }}+{\frac {\partial L}{\partial t}}\\-{\frac {\partial L}{\partial t}}&={\frac {d}{dt}}\left({\frac {\partial L}{\partial \mathbf {\dot {q}} }}\right){\dot {\mathbf {q} }}+{\ddot {\mathbf {q} }}{\frac {\partial L}{\partial \mathbf {\dot {q}} }}-{\dot {L}}\\-{\frac {\partial L}{\partial t}}&={\frac {d}{dt}}\left({\frac {\partial L}{\partial \mathbf {\dot {q}} }}\mathbf {\dot {q}} -L\right)={\frac {dH}{dt}}\end{aligned}}}$$

Si el lagrangiano L no depende explícitamente del tiempo, entonces ∂ L /∂ t = 0 , entonces H no varía con el tiempo, evolución de la partícula, de hecho, es una integral del movimiento, lo que significa que Por lo tanto, si las coordenadas elegidas fueran coordenadas naturales, la energía se conserva. $${\displaystyle H(\mathbf {q} (t),{\dot {\mathbf {q} }}(t),t)={\text{constant of time}}.}$$

Energías cinéticas y potenciales

En todas estas circunstancias, ^[42] la constante es la energía total del sistema. Las energías cinética y potencial siguen cambiando a medida que el sistema evoluciona, pero el movimiento del sistema será tal que su suma, la energía total, será constante. Esta es una simplificación valiosa, ya que la energía E es una constante de integración que cuenta como una constante arbitraria para el problema, y ​​puede ser posible integrar las velocidades a partir de esta relación de energía para resolver las coordenadas. $${\displaystyle E=T+V}$$

Similitud mecánica

Si la energía potencial es una función homogénea de las coordenadas e independiente del tiempo, ^[43] y todos los vectores de posición están escalados por la misma constante distinta de cero α , r _k ′ = α r _k , de modo que y el tiempo está escalado por un factor β , t ′ = βt , entonces las velocidades v _k están escaladas por un factor de α / β y la energía cinética T por ( α / β ) ² . Todo el Lagrangiano ha sido escalado por el mismo factor si $${\displaystyle V(\alpha \mathbf {r} _{1},\alpha \mathbf {r} _{2},\ldots ,\alpha \mathbf {r} _{N})=\alpha ^{N}V(\mathbf {r} _{1},\mathbf {r} _{2},\ldots ,\mathbf {r} _{N})}$$ $${\displaystyle {\frac {\alpha ^{2}}{\beta ^{2}}}=\alpha ^{N}\quad \Rightarrow \quad \beta =\alpha ^{1-{\frac {N}{2}}}.}$$

Como las longitudes y los tiempos se han escalado, las trayectorias de las partículas en el sistema siguen caminos geométricamente similares que difieren en tamaño. La longitud l recorrida en el tiempo t en la trayectoria original corresponde a una nueva longitud l ′ recorrida en el tiempo t ′ en la nueva trayectoria, dada por las razones $${\displaystyle {\frac {t'}{t}}=\left({\frac {l'}{l}}\right)^{1-{\frac {N}{2}}}.}$$

Partículas interactuantes

Para un sistema dado, si dos subsistemas A y B no interactúan, el lagrangiano L del sistema general es la suma de los lagrangianos L _A y L _B para los subsistemas: ^[38] $${\displaystyle L=L_{A}+L_{B}.}$$

Si interactúan, esto no es posible. En algunas situaciones, puede ser posible separar el lagrangiano del sistema L en la suma de los lagrangianos que no interactúan, más otro lagrangiano L _AB que contenga información sobre la interacción. $${\displaystyle L=L_{A}+L_{B}+L_{AB}.}$$

Esto puede estar motivado físicamente por considerar que los lagrangianos que no interactúan son solo energías cinéticas, mientras que el lagrangiano de interacción es la energía potencial total del sistema. Además, en el caso límite de interacción despreciable, L _AB tiende a cero, lo que reduce el valor al caso de no interacción mencionado anteriormente.

La extensión a más de dos subsistemas que no interactúan es sencilla: el lagrangiano general es la suma de los lagrangianos separados para cada subsistema. Si hay interacciones, se pueden agregar los lagrangianos de interacción.

Consecuencias de los lagrangianos singulares

De las ecuaciones de Euler-Lagrange se deduce que: $${\displaystyle {\begin{aligned}&{\frac {d}{dt}}{\frac {\partial L}{\partial {\dot {q}}_{i}}}-{\frac {\partial L}{\partial q_{i}}}=0\\&{\frac {\partial ^{2}L}{\partial q_{j}\partial {\dot {q}}_{i}}}{\frac {dq_{j}}{dt}}+{\frac {\partial ^{2}L}{\partial {\dot {q}}_{j}\partial {\dot {q}}_{i}}}{\frac {d{\dot {q}}_{j}}{dt}}+{\frac {\partial L}{\partial t}}-{\frac {\partial L}{\partial q_{i}}}=0\\&\sum _{j}W_{ij}(q,{\dot {q}},t){\ddot {q}}_{j}={\frac {\partial L}{\partial q_{i}}}-{\frac {\partial L}{\partial t}}-\sum _{j}{\frac {\partial ^{2}L}{\partial {\dot {q}}_{i}\partial q_{j}}}{\dot {q}}_{j},\\\end{aligned}}}$$

donde la matriz se define como . Si la matriz no es singular, las ecuaciones anteriores se pueden resolver para representar como una función de . Si la matriz no es invertible, no sería posible representar todas las como una función de pero, además, las ecuaciones de movimientos hamiltonianas no adoptarán la forma estándar. ^[44] ${\displaystyle W_{ij}={\frac {\partial ^{2}L}{\partial {\dot {q}}_{i}\partial {\dot {q}}_{j}}}}$ ${\displaystyle W}$ ${\displaystyle {\ddot {q}}}$ ${\displaystyle ({\dot {q}},q,t)}$ ${\displaystyle {\ddot {q}}}$ ${\displaystyle ({\dot {q}},q,t)}$

Ejemplos

Los siguientes ejemplos aplican las ecuaciones de Lagrange del segundo tipo a problemas mecánicos.

Fuerza conservadora

Una partícula de masa m se mueve bajo la influencia de una fuerza conservativa derivada del gradiente ∇ de un potencial escalar , $${\displaystyle \mathbf {F} =-{\boldsymbol {\nabla }}V(\mathbf {r} ).}$$

Si hay más partículas, de acuerdo con los resultados anteriores, la energía cinética total es una suma de todas las energías cinéticas de las partículas, y el potencial es una función de todas las coordenadas.

Coordenadas cartesianas

El lagrangiano de la partícula se puede escribir $${\displaystyle L(x,y,z,{\dot {x}},{\dot {y}},{\dot {z}})={\frac {1}{2}}m({\dot {x}}^{2}+{\dot {y}}^{2}+{\dot {z}}^{2})-V(x,y,z).}$$

Las ecuaciones de movimiento para la partícula se encuentran aplicando la ecuación de Euler-Lagrange para la coordenada x con derivadas de aquí y de manera similar para las coordenadas y y z . Recopilando las ecuaciones en forma vectorial encontramos que es la segunda ley de movimiento de Newton para una partícula sujeta a una fuerza conservativa. $${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial L}{\partial {\dot {x}}}}\right)={\frac {\partial L}{\partial x}},}$$ $${\displaystyle {\frac {\partial L}{\partial x}}=-{\frac {\partial V}{\partial x}},\quad {\frac {\partial L}{\partial {\dot {x}}}}=m{\dot {x}},\quad {\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial L}{\partial {\dot {x}}}}\right)=m{\ddot {x}},}$$ $${\displaystyle m{\ddot {x}}=-{\frac {\partial V}{\partial x}},}$$ $${\displaystyle m{\ddot {\mathbf {r} }}=-{\boldsymbol {\nabla }}V}$$

Coordenadas polares en 2D y 3D

Utilizando las coordenadas esféricas ( r , θ , φ ) como se usan comúnmente en física (convención ISO 80000-2:2019), donde r es la distancia radial al origen, θ es el ángulo polar (también conocido como colatitud, ángulo cenital, ángulo normal o ángulo de inclinación) y φ es el ángulo azimutal, el lagrangiano para un potencial central es Entonces, en coordenadas esféricas, las ecuaciones de Euler-Lagrange son La coordenada φ es cíclica ya que no aparece en el lagrangiano, por lo que el momento conservado en el sistema es el momento angular en el que r , θ y dφ / dt pueden variar con el tiempo, pero solo de tal manera que p _φ sea constante. $${\displaystyle L={\frac {m}{2}}({\dot {r}}^{2}+r^{2}{\dot {\theta }}^{2}+r^{2}\sin ^{2}\theta \,{\dot {\varphi }}^{2})-V(r).}$$ $${\displaystyle m{\ddot {r}}-mr({\dot {\theta }}^{2}+\sin ^{2}\theta \,{\dot {\varphi }}^{2})+{\frac {\partial V}{\partial r}}=0,}$$ $${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}(mr^{2}{\dot {\theta }})-mr^{2}\sin \theta \cos \theta \,{\dot {\varphi }}^{2}=0,}$$ $${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}(mr^{2}\sin ^{2}\theta \,{\dot {\varphi }})=0.}$$ $${\displaystyle p_{\varphi }={\frac {\partial L}{\partial {\dot {\varphi }}}}=mr^{2}\sin ^{2}\theta {\dot {\varphi }},}$$

El lagrangiano en coordenadas polares bidimensionales se recupera fijando θ en el valor constante π /2.

Péndulo sobre soporte móvil

Esquema de la situación con definición de las coordenadas (click para ampliar)

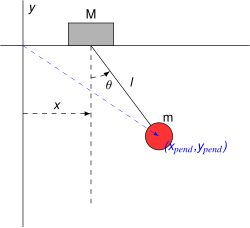
Consideremos un péndulo de masa m y longitud ℓ , que está unido a un soporte con masa M , que puede moverse a lo largo de una línea en la dirección . Sea la coordenada a lo largo de la línea del soporte, y denotemos la posición del péndulo por el ángulo desde la vertical. Las coordenadas y los componentes de velocidad del cuerpo del péndulo son ${\displaystyle x}$ ${\displaystyle x}$ ${\displaystyle \theta }$ $${\displaystyle {\begin{array}{rll}&x_{\mathrm {pend} }=x+\ell \sin \theta &\quad \Rightarrow \quad {\dot {x}}_{\mathrm {pend} }={\dot {x}}+\ell {\dot {\theta }}\cos \theta \\&y_{\mathrm {pend} }=-\ell \cos \theta &\quad \Rightarrow \quad {\dot {y}}_{\mathrm {pend} }=\ell {\dot {\theta }}\sin \theta .\end{array}}}$$

Las coordenadas generalizadas pueden tomarse como y . La energía cinética del sistema es entonces y la energía potencial es dando el lagrangiano ${\displaystyle x}$ ${\displaystyle \theta }$ $${\displaystyle T={\frac {1}{2}}M{\dot {x}}^{2}+{\frac {1}{2}}m\left({\dot {x}}_{\mathrm {pend} }^{2}+{\dot {y}}_{\mathrm {pend} }^{2}\right)}$$ $${\displaystyle V=mgy_{\mathrm {pend} }}$$ $${\displaystyle {\begin{array}{rcl}L&=&T-V\\&=&{\frac {1}{2}}M{\dot {x}}^{2}+{\frac {1}{2}}m\left[\left({\dot {x}}+\ell {\dot {\theta }}\cos \theta \right)^{2}+\left(\ell {\dot {\theta }}\sin \theta \right)^{2}\right]+mg\ell \cos \theta \\&=&{\frac {1}{2}}\left(M+m\right){\dot {x}}^{2}+m{\dot {x}}\ell {\dot {\theta }}\cos \theta +{\frac {1}{2}}m\ell ^{2}{\dot {\theta }}^{2}+mg\ell \cos \theta .\end{array}}}$$

Como x no está presente en la ecuación de Lagrange, se trata de una coordenada cíclica. El momento conservado es y la ecuación de Lagrange para la coordenada de apoyo es $${\displaystyle p_{x}={\frac {\partial L}{\partial {\dot {x}}}}=(M+m){\dot {x}}+m\ell {\dot {\theta }}\cos \theta ,}$$ ${\displaystyle x}$ $${\displaystyle (M+m){\ddot {x}}+m\ell {\ddot {\theta }}\cos \theta -m\ell {\dot {\theta }}^{2}\sin \theta =0.}$$

La ecuación de Lagrange para el ángulo θ es y simplificando $${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}\left[m({\dot {x}}\ell \cos \theta +\ell ^{2}{\dot {\theta }})\right]+m\ell ({\dot {x}}{\dot {\theta }}+g)\sin \theta =0;}$$ $${\displaystyle {\ddot {\theta }}+{\frac {\ddot {x}}{\ell }}\cos \theta +{\frac {g}{\ell }}\sin \theta =0.}$$

Estas ecuaciones pueden parecer bastante complicadas, pero encontrarlas con las leyes de Newton habría requerido identificar cuidadosamente todas las fuerzas, lo que habría sido mucho más laborioso y propenso a errores. Al considerar casos límite, se puede verificar la corrección de este sistema: por ejemplo, debe dar las ecuaciones de movimiento para un péndulo simple que está en reposo en algún marco inercial , mientras que debe dar las ecuaciones para un péndulo en un sistema en aceleración constante, etc. Además, es trivial obtener los resultados numéricamente, dadas las condiciones iniciales adecuadas y un paso de tiempo elegido, recorriendo los resultados iterativamente . ${\displaystyle {\ddot {x}}\to 0}$ ${\displaystyle {\ddot {\theta }}\to 0}$

Problema de fuerza central de dos cuerpos

Dos cuerpos de masas m ₁ y m ₂ con vectores de posición r ₁ y r ₂ están en órbita uno alrededor del otro debido a un potencial central atractivo V . Podemos escribir el Lagrangiano en términos de las coordenadas de posición tal como están, pero es un procedimiento establecido convertir el problema de dos cuerpos en un problema de un cuerpo de la siguiente manera. Introduzca las coordenadas de Jacobi ; la separación de los cuerpos r = r ₂ − r ₁ y la ubicación del centro de masas R = ( m ₁ r ₁ + m ₂ r ₂ )/( m ₁ + m ₂ ) . El Lagrangiano es entonces ^{[45] [46] [nb 4]} donde M = m ₁ + m ₂ es la masa total, μ = m ₁ m ₂ /( m ₁ + m ₂ ) es la masa reducida , y V el potencial de la fuerza radial, que depende solo de la magnitud de la separación | r | = | r ₂ − r ₁ | . El lagrangiano se divide en un término de centro de masa L _cm y un término de movimiento relativo L _rel . $${\displaystyle L=\underbrace {{\frac {1}{2}}M{\dot {\mathbf {R} }}^{2}} _{L_{\text{cm}}}+\underbrace {{\frac {1}{2}}\mu {\dot {\mathbf {r} }}^{2}-V(|\mathbf {r} |)} _{L_{\text{rel}}}}$$

La ecuación de Euler-Lagrange para R es simplemente la que establece que el centro de masa se mueve en línea recta a velocidad constante. $${\displaystyle M{\ddot {\mathbf {R} }}=0,}$$

Dado que el movimiento relativo sólo depende de la magnitud de la separación, lo ideal es utilizar coordenadas polares ( r , θ ) y tomar r = | r | , por lo que θ es una coordenada cíclica con el momento (angular) conservado correspondiente. $${\displaystyle L_{\text{rel}}={\frac {1}{2}}\mu \left({\dot {r}}^{2}+r^{2}{\dot {\theta }}^{2}\right)-V(r),}$$ $${\displaystyle p_{\theta }={\frac {\partial L_{\text{rel}}}{\partial {\dot {\theta }}}}=\mu r^{2}{\dot {\theta }}=\ell .}$$

La coordenada radial r y la velocidad angular d θ /d t pueden variar con el tiempo, pero sólo de tal manera que ℓ sea constante. La ecuación de Lagrange para r es $${\displaystyle \mu r{\dot {\theta }}^{2}-{\frac {dV}{dr}}=\mu {\ddot {r}}.}$$

Esta ecuación es idéntica a la ecuación radial obtenida utilizando las leyes de Newton en un sistema de referencia co-rotativo , es decir, un sistema que gira con la masa reducida de modo que parece estacionario. Eliminando la velocidad angular d θ /d t de esta ecuación radial, ^[47] que es la ecuación de movimiento para un problema unidimensional en el que una partícula de masa μ está sometida a la fuerza central hacia adentro −d V /d r y una segunda fuerza hacia afuera, llamada en este contexto fuerza centrífuga (lagrangiana) (ver fuerza centrífuga#Otros usos del término ): $${\displaystyle \mu {\ddot {r}}=-{\frac {\mathrm {d} V}{\mathrm {d} r}}+{\frac {\ell ^{2}}{\mu r^{3}}}.}$$ $${\displaystyle F_{\mathrm {cf} }=\mu r{\dot {\theta }}^{2}={\frac {\ell ^{2}}{\mu r^{3}}}.}$$

Por supuesto, si uno permanece completamente dentro de la formulación unidimensional, ℓ entra sólo como algún parámetro impuesto de la fuerza externa hacia afuera, y su interpretación como momento angular depende del problema bidimensional más general del cual se originó el problema unidimensional.

Si se llega a esta ecuación utilizando la mecánica newtoniana en un marco co-rotativo, la interpretación es evidente como la fuerza centrífuga en ese marco debido a la rotación del marco mismo. Si se llega a esta ecuación directamente utilizando las coordenadas generalizadas ( r , θ ) y simplemente siguiendo la formulación lagrangiana sin pensar en los marcos en absoluto, la interpretación es que la fuerza centrífuga es una consecuencia del uso de coordenadas polares . Como dice Hildebrand: ^[48]

"Como estas magnitudes no son verdaderas fuerzas físicas, se las suele llamar fuerzas de inercia . Su presencia o ausencia no depende del problema concreto en cuestión, sino del sistema de coordenadas elegido ". En particular, si se eligen coordenadas cartesianas, la fuerza centrífuga desaparece y la formulación implica únicamente la propia fuerza central, que proporciona la fuerza centrípeta para un movimiento curvo.

Este punto de vista, de que las fuerzas ficticias se originan en la elección de coordenadas, es expresado a menudo por los usuarios del método lagrangiano. Esta visión surge naturalmente en el enfoque lagrangiano, porque el marco de referencia es seleccionado (posiblemente inconscientemente) por la elección de coordenadas. Por ejemplo, véase ^[49] para una comparación de los lagrangianos en un marco de referencia inercial y en uno no inercial. Véase también la discusión de las formulaciones lagrangianas "totales" y "actualizadas" en. ^[50] Desafortunadamente, este uso de "fuerza inercial" entra en conflicto con la idea newtoniana de una fuerza inercial. En la visión newtoniana, una fuerza inercial se origina en la aceleración del marco de observación (el hecho de que no es un marco de referencia inercial ), no en la elección del sistema de coordenadas. Para mantener las cosas claras, es más seguro referirse a las fuerzas inerciales lagrangianas como fuerzas inerciales generalizadas , para distinguirlas de las fuerzas inerciales vectoriales newtonianas. Es decir, no se debe seguir a Hildebrand cuando dice (p. 155) " siempre tratamos con fuerzas, velocidades, aceleraciones y momentos generalizados . Para abreviar, el adjetivo "generalizado" se omitirá con frecuencia".

Se sabe que el lagrangiano de un sistema no es único. Dentro del formalismo lagrangiano las fuerzas ficticias newtonianas pueden identificarse por la existencia de lagrangianos alternativos en los que las fuerzas ficticias desaparecen, a veces hallados explotando la simetría del sistema. ^[51]

Extensiones para incluir fuerzas no conservativas

Fuerzas disipativas

La disipación (es decir, los sistemas no conservativos) también se puede tratar con un lagrangiano efectivo formulado por una cierta duplicación de los grados de libertad. ^{[52] [53] [54] [55]}

En una formulación más general, las fuerzas podrían ser tanto conservativas como viscosas . Si se puede encontrar una transformación apropiada a partir de F _i , Rayleigh sugiere utilizar una función de disipación , D , de la siguiente forma: ^[56] donde C _jk son constantes que están relacionadas con los coeficientes de amortiguamiento en el sistema físico, aunque no necesariamente iguales a ellos. Si D se define de esta manera, entonces ^[56] y $${\displaystyle D={\frac {1}{2}}\sum _{j=1}^{m}\sum _{k=1}^{m}C_{jk}{\dot {q}}_{j}{\dot {q}}_{k},}$$ $${\displaystyle Q_{j}=-{\frac {\partial V}{\partial q_{j}}}-{\frac {\partial D}{\partial {\dot {q}}_{j}}}}$$ $${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial L}{\partial {\dot {q}}_{j}}}\right)-{\frac {\partial L}{\partial q_{j}}}+{\frac {\partial D}{\partial {\dot {q}}_{j}}}=0.}$$

Electromagnetismo

Una partícula de prueba es una partícula cuya masa y carga se supone que son tan pequeñas que su efecto sobre el sistema externo es insignificante. A menudo es una partícula puntual simplificada hipotética sin propiedades distintas a la masa y la carga. Las partículas reales, como los electrones y los quarks up, son más complejas y tienen términos adicionales en sus lagrangianos. Los campos no solo pueden formar potenciales no conservativos, sino que estos potenciales también pueden depender de la velocidad.

El lagrangiano de una partícula cargada con carga eléctrica q , que interactúa con un campo electromagnético , es el ejemplo prototípico de un potencial dependiente de la velocidad. El potencial escalar eléctrico ϕ = ϕ ( r , t ) y el potencial vectorial magnético A = A ( r , t ) se definen a partir del campo eléctrico E = E ( r , t ) y el campo magnético B = B ( r , t ) de la siguiente manera: $${\displaystyle \mathbf {E} =-{\boldsymbol {\nabla }}\phi -{\frac {\partial \mathbf {A} }{\partial t}},\quad \mathbf {B} ={\boldsymbol {\nabla }}\times \mathbf {A} .}$$

El lagrangiano de una partícula de prueba cargada masiva en un campo electromagnético se denomina acoplamiento mínimo . Este es un buen ejemplo de cuándo la regla general común de que el lagrangiano es la energía cinética menos la energía potencial es incorrecta. Combinada con la ecuación de Euler-Lagrange , produce la ley de fuerza de Lorentz . $${\displaystyle L={\tfrac {1}{2}}m{\dot {\mathbf {r} }}^{2}+q\,{\dot {\mathbf {r} }}\cdot \mathbf {A} -q\phi ,}$$ $${\displaystyle m{\ddot {\mathbf {r} }}=q\mathbf {E} +q{\dot {\mathbf {r} }}\times \mathbf {B} }$$

Bajo la transformación de calibre : donde f ( r , t ) es cualquier función escalar del espacio y el tiempo, las transformadas lagrangianas antes mencionadas son como: que todavía produce la misma ley de fuerza de Lorentz. $${\displaystyle \mathbf {A} \rightarrow \mathbf {A} +{\boldsymbol {\nabla }}f,\quad \phi \rightarrow \phi -{\dot {f}},}$$ $${\displaystyle L\rightarrow L+q\left({\dot {\mathbf {r} }}\cdot {\boldsymbol {\nabla }}+{\frac {\partial }{\partial t}}\right)f=L+q{\frac {df}{dt}},}$$

Nótese que el momento canónico (conjugado a la posición r ) es el momento cinético más una contribución del campo A (conocido como momento potencial): $${\displaystyle \mathbf {p} ={\frac {\partial L}{\partial {\dot {\mathbf {r} }}}}=m{\dot {\mathbf {r} }}+q\mathbf {A} .}$$

This relation is also used in the minimal coupling prescription in quantum mechanics and quantum field theory. From this expression, we can see that the canonical momentum p is not gauge invariant, and therefore not a measurable physical quantity; However, if r is cyclic (i.e. Lagrangian is independent of position r), which happens if the ϕ and A fields are uniform, then this canonical momentum p given here is the conserved momentum, while the measurable physical kinetic momentum mv is not.

Other contexts and formulations

The ideas in Lagrangian mechanics have numerous applications in other areas of physics, and can adopt generalized results from the calculus of variations.

Alternative formulations of classical mechanics

A closely related formulation of classical mechanics is Hamiltonian mechanics. The Hamiltonian is defined by $${\displaystyle H=\sum _{i=1}^{n}{\dot {q}}_{i}{\frac {\partial L}{\partial {\dot {q}}_{i}}}-L}$$and can be obtained by performing a Legendre transformation on the Lagrangian, which introduces new variables canonically conjugate to the original variables. For example, given a set of generalized coordinates, the variables canonically conjugate are the generalized momenta. This doubles the number of variables, but makes differential equations first order. The Hamiltonian is a particularly ubiquitous quantity in quantum mechanics (see Hamiltonian (quantum mechanics)).

Routhian mechanics is a hybrid formulation of Lagrangian and Hamiltonian mechanics, which is not often used in practice but an efficient formulation for cyclic coordinates.

Momentum space formulation

The Euler–Lagrange equations can also be formulated in terms of the generalized momenta rather than generalized coordinates. Performing a Legendre transformation on the generalized coordinate Lagrangian L(q, dq/dt, t) obtains the generalized momenta Lagrangian L′(p, dp/dt, t) in terms of the original Lagrangian, as well the EL equations in terms of the generalized momenta. Both Lagrangians contain the same information, and either can be used to solve for the motion of the system. In practice generalized coordinates are more convenient to use and interpret than generalized momenta.

Higher derivatives of generalized coordinates

There is no mathematical reason to restrict the derivatives of generalized coordinates to first order only. It is possible to derive modified EL equations for a Lagrangian containing higher order derivatives, see Euler–Lagrange equation for details. However, from the physical point-of-view there is an obstacle to include time derivatives higher than the first order, which is implied by Ostrogradsky's construction of a canonical formalism for nondegenerate higher derivative Lagrangians, see Ostrogradsky instability

Optics

Lagrangian mechanics can be applied to geometrical optics, by applying variational principles to rays of light in a medium, and solving the EL equations gives the equations of the paths the light rays follow.

Relativistic formulation

Lagrangian mechanics can be formulated in special relativity and general relativity. Some features of Lagrangian mechanics are retained in the relativistic theories but difficulties quickly appear in other respects. In particular, the EL equations take the same form, and the connection between cyclic coordinates and conserved momenta still applies, however the Lagrangian must be modified and is not simply the kinetic minus the potential energy of a particle. Also, it is not straightforward to handle multiparticle systems in a manifestly covariant way, it may be possible if a particular frame of reference is singled out.

Quantum mechanics

In quantum mechanics, action and quantum-mechanical phase are related via the Planck constant, and the principle of stationary action can be understood in terms of constructive interference of wave functions.

In 1948, Feynman discovered the path integral formulation extending the principle of least action to quantum mechanics for electrons and photons. In this formulation, particles travel every possible path between the initial and final states; the probability of a specific final state is obtained by summing over all possible trajectories leading to it. In the classical regime, the path integral formulation cleanly reproduces Hamilton's principle, and Fermat's principle in optics.

Classical field theory

In Lagrangian mechanics, the generalized coordinates form a discrete set of variables that define the configuration of a system. In classical field theory, the physical system is not a set of discrete particles, but rather a continuous field ϕ(r, t) defined over a region of 3D space. Associated with the field is a Lagrangian density $${\displaystyle {\mathcal {L}}(\phi ,\nabla \phi ,{\dot {\phi }},\mathbf {r} ,t)}$$defined in terms of the field and its space and time derivatives at a location r and time t. Analogous to the particle case, for non-relativistic applications the Lagrangian density is also the kinetic energy density of the field, minus its potential energy density (this is not true in general, and the Lagrangian density has to be "reverse engineered"). The Lagrangian is then the volume integral of the Lagrangian density over 3D space $${\displaystyle L(t)=\int {\mathcal {L}}\,\mathrm {d} ^{3}\mathbf {r} }$$where d³r is a 3D differential volume element. The Lagrangian is a function of time since the Lagrangian density has implicit space dependence via the fields, and may have explicit spatial dependence, but these are removed in the integral, leaving only time in as the variable for the Lagrangian.

Noether's theorem

The action principle, and the Lagrangian formalism, are tied closely to Noether's theorem, which connects physical conserved quantities to continuous symmetries of a physical system.

If the Lagrangian is invariant under a symmetry, then the resulting equations of motion are also invariant under that symmetry. This characteristic is very helpful in showing that theories are consistent with either special relativity or general relativity.

See also

• Astronomy portal

• Canonical coordinates
• Fundamental lemma of the calculus of variations
• Functional derivative
• Generalized coordinates
• Hamiltonian mechanics
• Hamiltonian optics
• Inverse problem for Lagrangian mechanics, the general topic of finding a Lagrangian for a system given the equations of motion.
• Lagrangian and Eulerian specification of the flow field
• Lagrangian point
• Lagrangian system
• Non-autonomous mechanics
• Plateau's problem
• Restricted three-body problem

Footnotes

1. Sometimes in this context the variational derivative denoted and defined as $${\displaystyle {\frac {\delta }{\delta \mathbf {r} _{k}}}\equiv {\frac {\partial }{\partial \mathbf {r} _{k}}}-{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial }{\partial {\dot {\mathbf {r} }}_{k}}}}$$is used. Throughout this article only partial and total derivatives are used.
2. Here the virtual displacements are assumed reversible, it is possible for some systems to have non-reversible virtual displacements that violate this principle, see Udwadia–Kalaba equation.
3. In other words $${\displaystyle \mathbf {C} _{k}\cdot \delta \mathbf {r} _{k}=0}$$for particle k subject to a constraint force, however $${\displaystyle C_{k\,x}\delta x_{k}\neq 0,\quad C_{k\,y}\delta y_{k}\neq 0,\quad C_{k\,z}\delta z_{k}\neq 0}$$because of the constraint equations on the r_k coordinates.
4. The Lagrangian also can be written explicitly for a rotating frame. See Padmanabhan, 2000.

Notes

1. Fraser, Craig. "J. L. Lagrange's Early Contributions to the Principles and Methods of Mechanics". Archive for History of Exact Sciences, vol. 28, no. 3, 1983, pp. 197–241. JSTOR, http://www.jstor.org/stable/41133689. Accessed 3 Nov. 2023.
2. Hand & Finch 1998, p. 23
3. Hand & Finch 1998, pp. 18–20
4. Hand & Finch 1998, pp. 46, 51
5. Ball, Philip (2019-09-13). "Teaching Energy Before Forces". Physics. p. 100. doi:10.1103/PhysRevPhysEducRes.15.020126. Retrieved 2024-09-27.
6. Tatum, J. B. "Lagrangian mechanics" (PDF). www.astro.uvic.ca. Retrieved 2024-09-27.
7. Parsons, Paul; Dixon, Gail (2016). 50 ideas you really need to know : science. London: Quercus. pp. 4–7. ISBN 9781784296148.
8. Torby 1984, p. 270
9. Torby 1984, p. 269
10. Cremaschini, Claudio; Tessarotto, Massimo (2015-06-30). "Synchronous Lagrangian variational principles in General Relativity". The European Physical Journal Plus. 130 (6): 123. doi:10.1140/epjp/i2015-15123-4. ISSN 2190-5444.
11. Bersani AM, Caressa P. Lagrangian descriptions of dissipative systems: a review. Mathematics and Mechanics of Solids. 2021;26(6):785-803. Doi: 10.1177/1081286520971834
12. Hand & Finch 1998, p. 36–40
13. Pfeiffer, Friedrich (2008), Pfeiffer, Friedrich (ed.), "Constraint Systems", Mechanical System Dynamics, Berlin, Heidelberg: Springer, pp. 85–186, doi:10.1007/978-3-540-79436-3_3, ISBN 978-3-540-79436-3, retrieved 2024-09-23
14. Hand & Finch 1998, p. 60–61
15. Hand & Finch 1998, p. 19
16. Penrose 2007
17. Morin, D. (2007). Chapter 6: The Lagrangian Method. In The Lagrangian Method. https://scholar.harvard.edu/files/david-morin/files/cmchap6.pdf
18. Kay 1988, p. 156
19. Synge & Schild 1949, p. 150–152
20. Foster & Nightingale 1995, p. 89
21. Hand & Finch 1998, p. 4
22. Goldstein 1980, pp. 16–18
23. Hand & Finch 1998, p. 15
24. Hand & Finch 1998, p. 15
25. Fetter & Walecka 1980, p. 53
26. Kibble & Berkshire 2004, p. 234
27. Fetter & Walecka 1980, p. 56
28. Hand & Finch 1998, p. 17
29. Hand & Finch 1998, p. 15–17
30. R. Penrose (2007). The Road to Reality. Vintage books. p. 474. ISBN 978-0-679-77631-4.
31. Goldstein 1980, p. 23
32. Kibble & Berkshire 2004, p. 234–235
33. Hand & Finch 1998, p. 51
34. Hanc, Jozef; Taylor, Edwin F.; Tuleja, Slavomir (2005-07-01). "Variational mechanics in one and two dimensions". American Journal of Physics. 73 (7): 603–610. Bibcode:2005AmJPh..73..603H. doi:10.1119/1.1848516. ISSN 0002-9505.
35. Hand & Finch 1998, p. 44–45
36. Goldstein 1980
37. Fetter & Walecka 1980, pp. 68–70
38. Landau & Lifshitz 1976, p. 4
39. Goldstein, Poole & Safko 2002, p. 21
40. Landau & Lifshitz 1976, p. 4
41. Goldstein 1980, p. 21
42. Landau & Lifshitz 1976, p. 14
43. Landau & Lifshitz 1976, p. 22
44. Rothe, Heinz J; Rothe, Klaus D (2010). Classical and Quantum Dynamics of Constrained Hamiltonian Systems. World Scientific Lecture Notes in Physics. Vol. 81. WORLD SCIENTIFIC. p. 7. doi:10.1142/7689. ISBN 978-981-4299-64-0.
45. Taylor 2005, p. 297
46. Padmanabhan 2000, p. 48
47. Hand & Finch 1998, pp. 140–141
48. Hildebrand 1992, p. 156
49. Zak, Zbilut & Meyers 1997, pp. 202
50. Shabana 2008, pp. 118–119
51. Gannon 2006, p. 267
52. Kosyakov 2007
53. Galley 2013
54. Birnholtz, Hadar & Kol 2014
55. Birnholtz, Hadar & Kol 2013
56. Torby 1984, p. 271

References

• Lagrange, J. L. (1811). Mécanique analytique. Vol. 1.
• Lagrange, J. L. (1815). Mécanique analytique. Vol. 2.
• Penrose, Roger (2007). The Road to Reality. Vintage books. ISBN 978-0-679-77631-4.
• Landau, L. D.; Lifshitz, E. M. (15 January 1976). Mechanics (3rd ed.). Butterworth Heinemann. p. 134. ISBN 9780750628969.
• Landau, Lev; Lifshitz, Evgeny (1975). The Classical Theory of Fields. Elsevier Ltd. ISBN 978-0-7506-2768-9.
• Hand, L. N.; Finch, J. D. (1998). Analytical Mechanics (2nd ed.). Cambridge University Press. ISBN 9780521575720.
• Saletan, E. J.; José, J. V. (1998). Classical Dynamics: A Contemporary Approach. Cambridge University Press. ISBN 9780521636360.
• Kibble, T. W. B.; Berkshire, F. H. (2004). Classical Mechanics (5th ed.). Imperial College Press. p. 236. ISBN 9781860944352.
• Goldstein, Herbert (1980). Classical Mechanics (2nd ed.). San Francisco, CA: Addison Wesley. ISBN 0201029189.
• Goldstein, Herbert; Poole, Charles P. Jr.; Safko, John L. (2002). Classical Mechanics (3rd ed.). San Francisco, CA: Addison Wesley. ISBN 0-201-65702-3.
• Lanczos, Cornelius (1986). "II §5 Auxiliary conditions: the Lagrangian λ-method". The variational principles of mechanics (Reprint of University of Toronto 1970 4th ed.). Courier Dover. p. 43. ISBN 0-486-65067-7.
• Fetter, A. L.; Walecka, J. D. (1980). Theoretical Mechanics of Particles and Continua. Dover. pp. 53–57. ISBN 978-0-486-43261-8.
• The Principle of Least Action, R. Feynman
• Dvorak, R.; Freistetter, Florian (2005). "§ 3.2 Lagrange equations of the first kind". Chaos and stability in planetary systems. Birkhäuser. p. 24. ISBN 3-540-28208-4.
• Haken, H (2006). Information and self-organization (3rd ed.). Springer. p. 61. ISBN 3-540-33021-6.
• Henry Zatzkis (1960). "§1.4 Lagrange equations of the second kind". In DH Menzel (ed.). Fundamental formulas of physics. Vol. 1 (2nd ed.). Courier Dover. p. 160. ISBN 0-486-60595-7.
• Hildebrand, Francis Begnaud (1992). Methods of applied mathematics (Reprint of Prentice-Hall 1965 2nd ed.). Courier Dover. p. 156. ISBN 0-486-67002-3.
• Zak, Michail; Zbilut, Joseph P.; Meyers, Ronald E. (1997). From instability to intelligence. Springer. p. 202. ISBN 3-540-63055-4.
• Shabana, Ahmed A. (2008). Computational continuum mechanics. Cambridge University Press. pp. 118–119. ISBN 978-0-521-88569-0.
• Taylor, John Robert (2005). Classical mechanics. University Science Books. p. 297. ISBN 1-891389-22-X.
• Padmanabhan, Thanu (2000). "§2.3.2 Motion in a rotating frame". Theoretical Astrophysics: Astrophysical processes (3rd ed.). Cambridge University Press. p. 48. ISBN 0-521-56632-0.
• Doughty, Noel A. (1990). Lagrangian Interaction. Addison-Wesley Publishers Ltd. ISBN 0-201-41625-5.
• Kosyakov, B. P. (2007). Introduction to the classical theory of particles and fields. Berlin, Germany: Springer. doi:10.1007/978-3-540-40934-2. ISBN 978-3-540-40933-5.
• Galley, Chad R. (2013). "Classical Mechanics of Nonconservative Systems". Physical Review Letters. 110 (17): 174301. arXiv:1210.2745. Bibcode:2013PhRvL.110q4301G. doi:10.1103/PhysRevLett.110.174301. PMID 23679733. S2CID 14591873.
• Birnholtz, Ofek; Hadar, Shahar; Kol, Barak (2014). "Radiation reaction at the level of the action". International Journal of Modern Physics A. 29 (24): 1450132–1450190. arXiv:1402.2610. Bibcode:2014IJMPA..2950132B. doi:10.1142/S0217751X14501322. S2CID 118541484.
• Birnholtz, Ofek; Hadar, Shahar; Kol, Barak (2013). "Theory of post-Newtonian radiation and reaction". Physical Review D. 88 (10): 104037. arXiv:1305.6930. Bibcode:2013PhRvD..88j4037B. doi:10.1103/PhysRevD.88.104037. S2CID 119170985.
• Roger F Gans (2013). Engineering Dynamics: From the Lagrangian to Simulation. New York: Springer. ISBN 978-1-4614-3929-5.
• Gannon, Terry (2006). Moonshine beyond the monster: the bridge connecting algebra, modular forms and physics. Cambridge University Press. p. 267. ISBN 0-521-83531-3.
• Torby, Bruce (1984). "Energy Methods". Advanced Dynamics for Engineers. HRW Series in Mechanical Engineering. United States of America: CBS College Publishing. ISBN 0-03-063366-4.
• Foster, J; Nightingale, J.D. (1995). A Short Course in General Relativity (2nd ed.). Springer. ISBN 0-03-063366-4.
• M. P. Hobson; G. P. Efstathiou; A. N. Lasenby (2006). General Relativity: An Introduction for Physicists. Cambridge University Press. pp. 79–80. ISBN 9780521829519.
• Synge, J.L.; Schild, A. (1949). Tensor Calculus. first Dover Publications 1978 edition. ISBN 978-0-486-63612-2.
• Kay, David (April 1988). Schaum's Outline of Tensor Calculus. McGraw Hill Professional. ISBN 978-0-07-033484-7.

Further reading

• Gupta, Kiran Chandra, Classical mechanics of particles and rigid bodies (Wiley, 1988).
• Cassel, Kevin (2013). Variational methods with applications in science and engineering. Cambridge: Cambridge University Press. ISBN 978-1-107-02258-4.
• Goldstein, Herbert, et al. Classical Mechanics. 3rd ed., Pearson, 2002.

External links

• David Tong. "Cambridge Lecture Notes on Classical Dynamics". DAMTP. Retrieved 2017-06-08.
• Principle of least action interactive Excellent interactive explanation/webpage
• Joseph Louis de Lagrange - Œuvres complètes (Gallica-Math)
• Constrained motion and generalized coordinates, page 4