En física, el efecto magnetoóptico Kerr ( MOKE ) o el efecto magnetoóptico Kerr de superficie ( SMOKE ) es uno de los efectos magnetoópticos . Describe los cambios en la luz reflejada desde una superficie magnetizada . Se utiliza en la investigación de la ciencia de los materiales en dispositivos como el microscopio Kerr, para investigar la estructura de magnetización de los materiales.

El efecto magneto-óptico Kerr se manifiesta cuando la luz se refleja desde una superficie magnetizada y puede cambiar tanto la polarización como la intensidad reflejada . El efecto magneto-óptico Kerr es similar al efecto Faraday , que describe los cambios en la transmisión de la luz a través de un material magnético. Por el contrario, el efecto magneto-óptico Kerr describe los cambios en la luz reflejada desde una superficie magnética. Ambos efectos son resultado de los componentes fuera de la diagonal del tensor dieléctrico . Estos componentes fuera de la diagonal le dan al material magneto-óptico una permitividad anisotrópica , lo que significa que su permitividad es diferente en diferentes direcciones. La permitividad afecta la velocidad de la luz en un material:
donde es la velocidad de la luz a través del material, es la permitividad del material y es la permeabilidad magnética; por lo tanto, la velocidad de la luz varía según su orientación. Esto provoca fluctuaciones en la fase de la luz incidente polarizada.
Este efecto se cuantifica a menudo en términos de su ángulo Kerr y su elipticidad Kerr. El ángulo Kerr es el ángulo en el que la luz polarizada linealmente rotará después de incidir en la muestra. La elipticidad Kerr ( o elipticidad de las matemáticas) es la relación entre los semiejes mayor y menor de la luz polarizada elípticamente, generada a partir de la reflexión de la luz polarizada linealmente. [1]
MOKE se puede clasificar además por la dirección del vector de magnetización con respecto a la superficie reflectante y el plano de incidencia.

Cuando el vector de magnetización es perpendicular a la superficie de reflexión y paralelo al plano de incidencia, el efecto se denomina efecto Kerr polar . Para simplificar el análisis, y debido a que las otras dos configuraciones tienen una rotación de Kerr que se desvanece en la incidencia normal, se suele emplear la incidencia casi normal cuando se realizan experimentos en la geometría polar.
En el efecto longitudinal, el vector de magnetización es paralelo tanto a la superficie de reflexión como al plano de incidencia. La configuración longitudinal implica que la luz se refleja en un ángulo desde la superficie de reflexión y no es normal a ella, como se utiliza para MOKE polar. De la misma manera, la luz polarizada linealmente que incide sobre la superficie se polariza elípticamente, y el cambio de polarización es directamente proporcional al componente de magnetización que es paralelo a la superficie de reflexión y paralelo al plano de incidencia. Esta luz polarizada elípticamente de primer orden tiene dos vectores perpendiculares, a saber, el coeficiente de reflexión de amplitud de Fresnel estándar y el coeficiente de Kerr . El coeficiente de Kerr suele ser mucho menor que el coeficiente de reflexión.
Cuando la magnetización es perpendicular al plano de incidencia y paralela a la superficie se dice que está en configuración transversal . En este caso, la luz incidente tampoco es normal a la superficie de reflexión sino que en lugar de medir la polaridad de la luz después de la reflexión, se mide la reflectividad. Este cambio en la reflectividad es proporcional al componente de magnetización que es perpendicular al plano de incidencia y paralelo a la superficie, como se indicó anteriormente. Si el componente de magnetización apunta a la derecha del plano incidente, visto desde la fuente, entonces el vector de Kerr se suma al vector de amplitud de Fresnel y la intensidad de la luz reflejada es . Por otro lado, si el componente del componente de magnetización apunta a la izquierda del plano incidente visto desde la fuente, el vector de Kerr se resta de la amplitud de Fresnel y la intensidad reflejada viene dada por .
Además del efecto Kerr polar , longitudinal y transversal que dependen linealmente de los respectivos componentes de magnetización, también existen efectos cuadráticos de orden superior, [2] para los cuales el ángulo Kerr depende de términos de producto que involucran los componentes de magnetización polar , longitudinal y transversal . Esos efectos se conocen como efecto Voigt o efecto Kerr cuadrático. El efecto Kerr magneto-óptico cuadrático (QMOKE) se encuentra fuerte en aleaciones Heusler como Co2FeSi y Co2MnGe [ 3] [4]
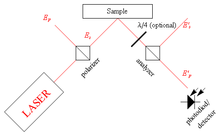
Un microscopio Kerr se basa en el MOKE para obtener imágenes de las diferencias en la magnetización de una superficie de material magnético. En un microscopio Kerr, la luz de iluminación pasa primero a través de un filtro polarizador , luego se refleja desde la muestra y pasa a través de un filtro polarizador analizador , antes de pasar por un microscopio óptico normal. Debido a que las diferentes geometrías del MOKE requieren una luz polarizada diferente, el polarizador debe tener la opción de cambiar la polarización de la luz incidente (circular, lineal y elíptica). Cuando la luz polarizada se refleja en el material de la muestra, puede producirse un cambio en cualquier combinación de los siguientes factores: rotación de Kerr, elipticidad de Kerr o amplitud polarizada. El analizador convierte los cambios de polarización en cambios en la intensidad de la luz, que son visibles. A menudo se utiliza un sistema informático para crear una imagen del campo magnético en la superficie a partir de estos cambios de polarización.
Las unidades magneto-ópticas (MO) se introdujeron en 1985. Los discos MO se escriben utilizando un láser y un electroimán. El láser calentaría el plato por encima de su temperatura de Curie , momento en el que el electroimán orientaría ese bit como un 1 o un 0. Para leer, el láser se hace funcionar a una intensidad menor y emite luz polarizada. La luz reflejada se analiza y muestra una diferencia notable entre un 0 o un 1.
El efecto magneto-óptico Kerr fue descubierto en 1877 por John Kerr . [5] [6]