El método de Romberg

Método de integración numérica

En el análisis numérico , se utiliza el método de Romberg ^{[1] para estimar la} integral definida aplicando la extrapolación de Richardson ^[2] repetidamente sobre la regla del trapecio o la regla del rectángulo (regla del punto medio). Las estimaciones generan una matriz triangular . El método de Romberg es una fórmula de Newton-Cotes : evalúa el integrando en puntos espaciados de manera uniforme. El integrando debe tener derivadas continuas, aunque se pueden obtener resultados bastante buenos si solo existen unas pocas derivadas. Si es posible evaluar el integrando en puntos espaciados de manera desigual, entonces otros métodos como la cuadratura gaussiana y la cuadratura de Clenshaw-Curtis son generalmente más precisos. $${\displaystyle \int _{a}^{b}f(x)\,dx}$$

El método lleva el nombre de Werner Romberg , quien lo publicó en 1955.

Método

Usando , el método puede definirse inductivamente por donde y . En notación O grande , el error para R ( n ,  m ) es: ^[3] ${\textstyle h_{n}={\frac {(b-a)}{2^{n}}}}$ $${\displaystyle {\begin{aligned}R(0,0)&=h_{1}(f(a)+f(b))\\R(n,0)&={\tfrac {1}{2}}R(n-1,0)+h_{n}\sum _{k=1}^{2^{n-1}}f(a+(2k-1)h_{n})\\R(n,m)&=R(n,m-1)+{\tfrac {1}{4^{m}-1}}(R(n,m-1)-R(n-1,m-1))\\&={\frac {1}{4^{m}-1}}(4^{m}R(n,m-1)-R(n-1,m-1))\end{aligned}}}$$ ${\displaystyle n\geq m}$ ${\displaystyle m\geq 1\,}$ ${\displaystyle O\left(h_{n}^{2m+2}\right).}$

La extrapolación cero, R ( n , 0) , es equivalente a la regla trapezoidal con 2 ⁿ + 1 puntos; la primera extrapolación, R ( n , 1) , es equivalente a la regla de Simpson con 2 ⁿ + 1 puntos. La segunda extrapolación, R ( n , 2) , es equivalente a la regla de Boole con 2 ⁿ + 1 puntos. Las extrapolaciones posteriores difieren de las fórmulas de Newton-Cotes. En particular, las extrapolaciones de Romberg posteriores amplían la regla de Boole de formas muy leves, modificando los pesos en proporciones similares a las de la regla de Boole. Por el contrario, los métodos de Newton-Cotes posteriores producen pesos cada vez más diferentes, lo que finalmente conduce a pesos positivos y negativos grandes. Esto es indicativo de cómo los métodos de Newton-Cotes de polinomios de interpolación de gran grado no convergen para muchas integrales, mientras que la integración de Romberg es más estable.

Al etiquetar nuestras aproximaciones como en lugar de , podemos realizar la extrapolación de Richardson con la fórmula de error definida a continuación: Una vez que hayamos obtenido nuestras aproximaciones , podemos etiquetarlas como . ${\textstyle O(h^{2})}$ ${\textstyle A_{0}{\big (}{\frac {h}{2^{n}}}{\big )}}$ ${\textstyle R(n,0)}$ $${\displaystyle \int _{a}^{b}f(x)\,dx=A_{0}{\bigg (}{\frac {h}{2^{n}}}{\bigg )}+a_{0}{\bigg (}{\frac {h}{2^{n}}}{\bigg )}^{2}+a_{1}{\bigg (}{\frac {h}{2^{n}}}{\bigg )}^{4}+a_{2}{\bigg (}{\frac {h}{2^{n}}}{\bigg )}^{6}+\cdots }$$ ${\textstyle O(h^{2(m+1)})}$ ${\textstyle A_{m}{\big (}{\frac {h}{2^{n}}}{\big )}}$ ${\textstyle R(n,m)}$

Cuando las evaluaciones de funciones son costosas, puede ser preferible reemplazar la interpolación polinomial de Richardson con la interpolación racional propuesta por Bulirsch y Stoer (1967).

Un ejemplo geométrico

Para estimar el área bajo una curva se aplica la regla del trapezoide primero a una pieza, luego a dos, luego a cuatro, y así sucesivamente.

De una sola pieza. Nótese que, como comienza y termina en cero, esta aproximación da como resultado un área cero.

De dos piezas

Cuatro piezas

Ocho piezas

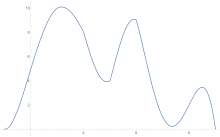
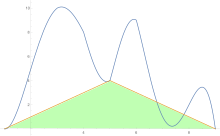
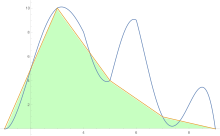
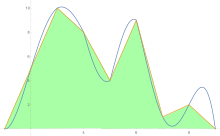
Después de obtener las estimaciones de la regla trapezoidal, se aplica la extrapolación de Richardson .

• Para la primera iteración, se utilizan las estimaciones de dos piezas y de una pieza en la fórmula .4 × (más preciso) − (menos preciso)/3⁠ . Luego se utiliza la misma fórmula para comparar la estimación de cuatro piezas y la de dos piezas, y lo mismo para las estimaciones más altas.
• Para la segunda iteración se utilizan los valores de la primera iteración en la fórmula16 × (más preciso) − (menos preciso)/15⁠
• La tercera iteración utiliza la siguiente potencia de 4 :64 × (más preciso) − (menos preciso)/63⁠ sobre los valores derivados de la segunda iteración.
• El patrón continúa hasta que haya una sola estimación.

Ejemplo

Como ejemplo, la función gaussiana se integra de 0 a 1, es decir, la función de error erf(1) ≈ 0,842700792949715. La matriz triangular se calcula fila por fila y el cálculo finaliza si las dos últimas entradas de la última fila difieren menos de 10 ⁻⁸ .

0,771743330,82526296 0,843102830,83836778 0,84273605 0,842711600,84161922 0,84270304 0,84270083 0,842700660,84243051 0,84270093 0,84270079 0,84270079 0,84270079

El resultado que aparece en la esquina inferior derecha de la matriz triangular es exacto a los dígitos que se muestran. Es notable que este resultado se derive de las aproximaciones menos exactas obtenidas con la regla del trapecio en la primera columna de la matriz triangular.

Implementación

A continuación se muestra un ejemplo de una implementación informática del método Romberg (en el lenguaje de programación C ):

#incluir <stdio.h> #incluir <math.h>  void print_row ( tamaño_t i , double * R ) { printf ( "R[%2zu] = " , i ); for ( tamaño_t j = 0 ; j <= i ; ++ j ) { printf ( "%f" , R [ j ]); } printf ( " \n " ); }                     /* ENTRADA: (*f) : puntero a la función a integrar a : límite inferior b : límite superior max_steps: pasos máximos del procedimiento acc : precisión deseadaSALIDA: Rp[max_steps-1]: valor aproximado de la integral de la función f para x en [a,b] con precisión 'acc' y pasos 'max_steps'. */ double romberg ( double ( * f )( double ), double a , double b , size_t max_steps , double acc ) { double R1 [ max_steps ], R2 [ max_steps ]; // buffers double * Rp = & R1 [ 0 ], * Rc = & R2 [ 0 ]; // Rp es la fila anterior, Rc es la fila actual double h = b - a ; //tamaño del paso Rp [ 0 ] = ( f ( a ) + f ( b )) * h * 0.5 ; //primer paso trapezoidal                                   imprimir_fila ( 0 , Rp );  para ( tamaño_t i = 1 ; i < máx_pasos ; ++ i ) { h /= 2. ; doble c = 0 ; tamaño_t ep = 1 << ( i -1 ); //2^(n-1) para ( tamaño_t j = 1 ; j <= ep ; ++ j ) { c += f ( a + ( 2 * j -1 ) * h ); } Rc [ 0 ] = h * c + .5 * Rp [ 0 ]; // R(i,0)                                                para ( tamaño_t j = 1 ; j <= i ; ++ j ) { doble n_k = pow ( 4 , j ); Rc [ j ] = ( n_k * Rc [ j -1 ] - Rp [ j -1 ]) / ( n_k -1 ); // calcular R(i,j) }                        // Imprimir la i-ésima fila de R, R[i,i] es la mejor estimación hasta el momento print_row ( i , Rc );   si ( i > 1 && fabs ( Rp [ i -1 ] - Rc [ i ]) < acc ) { devolver Rc [ i ]; }            // intercambiamos Rn y Rc ya que solo necesitamos la última fila double * rt = Rp ; Rp = Rc ; Rc = rt ; } return Rp [ max_steps -1 ]; // devolvemos nuestra mejor estimación }              

Aquí hay una implementación del método Romberg (en el lenguaje de programación Python ):

def  print_row ( i ,  R ): """Imprime una fila de la tabla de Romberg.""" print ( f "R[ { i : 2d } ]=" , end = " ) for j in range ( i + 1 ): print ( f " { R [ j ] : f } =" , end = " ) print ()            def  romberg ( f ,  a ,  b ,  max_steps ,  acc ): """  Calcula la integral de una función utilizando la integración de Romberg.  Args:  f: La función a integrar.  a: Límite inferior de integración.  b: Límite superior de integración.  max_steps: Número máximo de pasos.  acc: Precisión deseada. Devuelve:  El valor aproximado de la integral.  """  R1 ,  R2  =  [ 0 ]  *  max_steps ,  [ 0 ]  *  max_steps  # Buffers para almacenar filas  Rp ,  Rc  =  R1 ,  R2  # Punteros a filas anteriores y actuales h  =  b  -  a  # Tamaño del paso  Rp [ 0 ]  =  0.5  *  h  *  ( f ( a )  +  f ( b ))  # Primer paso trapezoidal imprimir_fila ( 0 ,  Rp ) para  i  en  el rango ( 1 ,  max_steps ):  h  /=  2.  c  =  0  ep  =  1  <<  ( i  -  1 )  # 2^(i-1)  para  j  en  el rango ( 1 ,  ep  +  1 ):  c  +=  f ( a  +  ( 2  *  j  -  1 )  *  h )  Rc [ 0 ]  =  h  *  c  +  0.5  *  Rp [ 0 ]  # R(i,0) para  j  en  el rango ( 1 ,  i  +  1 ):  n_k  =  4 ** j  Rc [ j ]  =  ( n_k  *  Rc [ j  -  1 ]  -  Rp [ j  -  1 ])  /  ( n_k  -  1 )  # Calcular R(i,j) # Imprimir la i-ésima fila de R, R[i,i] es la mejor estimación hasta el momento  print_row ( i ,  Rc ) si  i  >  1  y  abs ( Rp [ i  -  1 ]  -  Rc [ i ])  <  acc :  devuelve  Rc [ i ] # Intercambia Rn y Rc para la siguiente iteración  Rp ,  Rc  =  Rc ,  Rp devuelve  Rp [ max_steps  -  1 ]  # Devuelve nuestra mejor estimación

Referencias

Citas

1. Romberg 1955
2. Richardson 1911
3. Mysovskikh 2002

Bibliografía

• Richardson, LF (1911), "La solución aritmética aproximada por diferencias finitas de problemas físicos que involucran ecuaciones diferenciales, con una aplicación a las tensiones en una presa de mampostería", Philosophical Transactions of the Royal Society A , 210 (459–470): 307–357, Bibcode :1911RSPTA.210..307R, doi :10.1098/rsta.1911.0009, JSTOR  90994
• Romberg, W. (1955), "Vereinfachte numerische Integration", Det Kongelige Norske Videnskabers Selskab Forhandlinger , 28 (7), Trondheim: 30–36
• Thacher Jr., Henry C. (julio de 1964), "Observación sobre el algoritmo 60: integración de Romberg", Communications of the ACM , 7 (7): 420–421, doi : 10.1145/364520.364542
• Bauer, FL; Rutishauser, H.; Stiefel, E. (1963), Metropolis, NC; et al. (eds.), "Nuevos aspectos en la cuadratura numérica", Aritmética experimental, computación de alta velocidad y matemáticas, Actas de simposios en matemáticas aplicadas (15), AMS : 199–218
• Bulirsch, Roland; Stoer, Josef (1967), "Handbook Series Numerical Integration. Cuadratura numérica por extrapolación", Numerische Mathematik , 9 : 271–278, doi :10.1007/bf02162420
• Mysovskikh, IP (2002) [1994], "Método Romberg", en Hazewinkel, Michiel (ed.), Encyclopedia of Mathematics , Springer-Verlag , ISBN 1-4020-0609-8
• Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007), "Sección 4.3. Integración de Romberg", Recetas numéricas: el arte de la computación científica (3.ª ed.), Nueva York: Cambridge University Press, ISBN 978-0-85-0-312-0 978-0-521-88068-8

Enlaces externos

• ROMBINT – código para MATLAB (autor: Martin Kacenak)
• Herramienta de integración en línea gratuita que utiliza Romberg, Fox–Romberg, Gauss–Legendre y otros métodos numéricos
• Implementación del método de Romberg en SciPy
• Romberg.jl: implementación de Julia (compatible con factorizaciones arbitrarias, no solo puntos) ${\displaystyle 2^{n}+1}$